基于差分進化變分模態分解的直升機行星輪系故障監測

孫燦飛，彭德潤

（1.上海工程技術大學航空運輸學院，上海 201620；2.航空工業上海航空測控技術研究所測控技術產品部，上海 201601）

近年來，航空裝備故障診斷技術發展迅猛，在飛機和發動機的健康管理系統中得到廣泛應用。相比其他故障，早期故障引起的振動信號幅度較小，容易淹沒在正常的振動信號背景中，尤其對于行星輪系復雜的信號形態，微弱的故障信號更加難以捕捉。因此，早期故障更容易被忽略，而一旦故障持續發展將導致后期嚴重的飛行安全事故。2016 年，挪威一架H225“超級美洲豹”直升機墜毀，就是因為結構疲勞造成的行星輪系早期裂紋沒有及時得到預警，最終造成災難性的事故。因此，開展直升機行星輪系故障監測方法的研究具有重要的意義［1］。

直升機主減速器內部復雜的齒輪傳動形式和行星輪系自身獨特的齒輪結構造成傳感器測量到的振動信號呈現出非常復雜的信號形態［2］。首先，行星輪系所在的主減速器內各齒輪部件內部結構緊湊，各齒輪部件旋轉頻率和諧頻及故障特征頻率等多頻率成分組合在嚙合頻率和諧頻附近，形成復雜邊帶信號，且多階諧波出現頻譜交織，使信號更加復雜。其次，行星輪系本身的振動信號成分復雜，包括出現在行星齒輪運行過程中的特征頻率成分、出現在嚙合頻率和諧頻附近的成組邊帶成分、經多界面耦合傳播而來的支承軸承和其他定軸齒輪等旋轉部件的特征頻率成分等。再次，行星輪系故障，尤其是早期故障引起的微弱振動信號經傳感器復雜傳輸路徑衰減后，信號被進一步削弱，且大傳動比決定了齒輪故障信號的特征頻率極低，加之低速重載的復雜運行條件使得低頻振動成分的噪聲污染非常嚴重。因此，如何從具有復雜信號背景的直升機行星輪系振動信號中削弱甚至消除非故障敏感信號分量的干擾，增強故障敏感信號分量并進行有效提取是直升機行星輪系故障監測研究的熱點和難點。

根據行星齒輪箱振動信號理論模型與頻譜特性，齒輪故障會引起嚙合頻率及其諧頻附近的邊帶頻譜變化［3］，提取邊帶信號中含有故障齒輪特征頻率的信息進行故障識別，可解決復雜信號背景造成的故障頻率特征提取難題，提高診斷準確率［4］。因此采用模態分解與聯合解調的方法得到了廣泛關注。

Zhao等［5］應用經驗模態分解（Empirical Mode Decomposition，EMD）方法分解行星齒輪箱的振動信號，并從中遴選敏感分量提取故障特征進行故障診斷。由于EMD方法易產生模態混疊、過包絡、欠包絡等問題，Smith等［6］提出了局部均值分解方法，但其抗干擾能力差，算法不易收斂。Frei 等［7］提出了本征時間尺度分解方法，消除了邊緣效應和負頻率等的影響，瞬時頻率的計算精度較高，適用于非平穩非線性信號，但仍然存在信號失真等問題。李志農等［8］應用經驗小波分解方法有效識別了轉子碰摩故障，該方法解決了模態混疊等難題，但需要指定頻帶數量，對于復雜振動信號來說容易損失含有故障信息的邊頻帶信息。2014 年，Dragomiretskiy 等［9］提出了變分模態分解（Variational Mode Decomposition，VMD）算法，其廣泛應用于機械故障診斷領域［10-11］，該方法是一種非遞歸的分解算法，不存在端點效應，可有效分離頻率接近的諧波信號，且具有較好的噪聲魯棒性。

針對直升機行星輪系故障監測中復雜信號背景帶來的難題，本文提出了基于差分進化變分模態分解（Differential Evolution Variational Mode Decomposition，DEVMD）的直升機行星輪系故障監測方法。本方法集成了重疊組收縮（Overlapping Group Shrinkage，OGS）算法作為前置濾波對背景噪聲進行抑制，結合DEVMD方法高性能的模態分解能力剝離出振動信號中其他旋轉部件的信號分量，獲得行星輪系的故障敏感信號分量并提取故障指示因子，實現了直升機行星傳動輪系的故障監測。

1 故障監測理論與方法

1.1 基于OGS的前置降噪

由于傳感器測量的故障信號微弱，低速重載的運行條件和惡劣的工作環境導致信號容易受到背景噪聲的干擾，盡管相比于其他信號分解方法，VMD 算法的噪聲魯棒性較好，但噪聲增大到一定程度后，用該方法進行信號分解仍然會出現模態混疊、中心頻率偏移等現象，導致模態分解錯誤，因此在進行后續的信號處理之前，須進行前置降噪。

近年來，基于稀疏性的信號去噪、去卷積、恢復、重構等算法得到了廣泛的應用。2014 年，Chen 等［12］提出了OGS算法，該算法適應于具有成組稀疏特性（即大幅值數據以組的形式存在）的信號，非常適用于對故障引起的周期性沖擊信號的降噪。OGS 算法基于重疊組的收縮，將具有相同組特性的稀疏信號進行等比例處理，因此具備平移不變性，避免了塊效應，在最大化有用信息的同時抑制了噪聲信號。OGS 算法的優點包括：①轉化信號降噪問題為最優化問題進行求解，得到的稀疏解中大幅值信號成分得到有效保留，在抑制噪聲的同時有效保留了信號中的有用成分；②計算復雜度低且不需要調節算法參數。因此本文引入OGS算法作為前置降噪方法，抑制背景噪聲，降低噪聲方差，提高了VMD算法的分解性能。

假定信號表達式為

式中：y（i）為振動傳感器測量的含噪信號；x（i）為具有成組稀疏性的有用信號；w（i）為環境背景噪聲；I ＝｛0，1，…，N-1｝，N為數據點數量。

為從y（i）中最大程度估計出x（i），OGS算法將式（1）表達的信號降噪問題轉化為最優化問題：

罰函數R［x（i）］的定義為

式中：J ＝｛0，1，…，M-1｝，M為組數。

因此，最終的代價函數為

OGS算法流程如下。

①確定輸入信號和參數：y、λ、M。

②確定輸出信號：x。

③初始化：x（i）＝y（i），x（i）≠0。

⑥重復步驟④和步驟⑤，直到滿足收斂條件。

⑦得到降噪后的信號x。

1.2 基于DEVMD方法的故障敏感信號分量提取

在直升機行星輪系的振動信號頻譜中，除了有與行星輪系故障相關的信號分量外，還包括一級減速主從動齒輪、二級減速主從動齒輪、尾傳動齒輪和各附件齒輪等部件的嚙合振動信號分量。為了消除其他無關信號分量的影響，有效提取行星輪系的故障敏感信號分量，本文提出了基于DEVMD 方法的故障敏感信號分量提取方法。該方法結合VMD 算法與差分進化（Differential Evolution，DE）算法對振動信號進行自適應分解，從分解后的模態分量中遴選出最優故障敏感信號分量進行包絡譜分析與故障識別。

相比于其他模態分解方法，VMD算法避免了模態混疊與端點效應，具有可分解頻率相近成分等優點，其分解的精度主要受到以下兩個參數影響。

①模態數量K。K確定了要分解的模態分量的數量，并可根據K 采用均勻分布、隨機取值和賦值零等方式初始化中心頻率。K 取值過小，模態分量之間會產生混疊；K 取值過大，模態分量的完整性會受到影響，同時會增加計算復雜度。

②懲罰因子α。α 實現了對帶寬的約束：α 取值過小，分解得到的模態分量的帶寬過大，對噪聲的魯棒性就較差，且各模態分量間可能出現交叉；α 取值過大，分解得到的模態分量的帶寬過小，就容易出現中心頻率偏移的情況，導致分解失敗。

針對K與α的選擇，文獻［13］以包絡譜熵為目標函數，采用粒子群算法對VMD 算法的最佳參數組合進行搜索，實驗結果表明該方法的分析效果準確有效。文獻［14］為了自適應確定變分模態分解的模態數量，以互信息為判據對原方法進行了迭代停止條件的改進，結合Teager 能量算子對單分量信號解調速度快、精度高的優點，提出了Teager-VMD時頻分析方法。上述方法針對VMD 算法的參數選取，主要采用智能算法進行多次迭代優化選取，存在計算時間長、效率低等缺陷。另外，VMD算法的中心頻率采用隨機和均勻分配兩種方法，當中心頻率誤差較大時，無法正確實現信號分解。

針對上述情況，本文提出了自適應參數的DEVMD方法，利用功率譜密度先驗知識初始化中心頻率，并基于正交能量差采用DE 算法搜尋最佳的K與α的組合，詳細處理流程如圖1 所示。該方法既保證了模態分解的準確性，又保證了分解的模態分量具有一定的物理意義。

圖1 DEVMD方法處理流程

DEVMD方法的詳細處理流程如下。

①輸入原始信號x（t）。

②計算信號的功率譜密度，按照功率譜密度峰值由大到小搜索前Kmax個峰值，并記錄其相對應的頻率，組成中心頻率初始值集合｛ωinitial｝。

③初始化DE算法的參數，包括種群規模N、縮放比例因子F和交叉概率CR。

④初始化種群pi＝（pi，1，pi，2，…，pi，D），i ＝1，2，…，N，D為維數；初始化種群個體對應的中心頻率，從｛ωinitial｝中抽取前K個頻率作為初始化中心頻率。

⑤在當前種群所有個體對應的（K，α）組合下，對輸入原始信號進行VMD分解。

⑥計算個體適應度值。由于輸入振動信號所分解的各模態分量具有各自的物理意義，彼此獨立，具備正交性，根據帕塞瓦爾定理，分解的正交模態分量的能量之和與原始信號的能量相等，因此本文選取正交能量差作為DE算法優化的適應度函數：

⑦若個體適應度值滿足收斂閾值的要求，即Ediff≤（0.01 ～0.02）Ex，則停止尋優，否則進行種群進化。

⑧對當前種群進行差分進化，產生新一代種群。

a.變異操作。

式中：g為進化的代數；r1，r2，r3∈（1，2，…，N），與i 均互不相同。

b.交叉操作。

式中：j∈（1，2，…，D）；r為［0，1］的隨機整數。

c.選擇操作。

基于貪婪機制在父代個體與交叉后向量中選擇子代個體，通過式（8）確定。

式中：f為個體的適應度函數。

⑨若當前進化代數滿足中止條件，則停止尋優，否則繼續進行尋優。

⑩停止尋優，得到最優適應度值個體所對應的（K，α）組合。

1.3 基于峭度-包絡譜熵的故障監測

從分解的BIMF分量中選取中心頻率在行星傳動輪系嚙合頻率附近的分量作為故障敏感信號分量，選取峭度-包絡譜熵（Kurtosis-Envelope Spectrum Entropy，KE）作為故障指示因子實現故障監測。

峭度是反映隨機變量分布特性的數值統計量，是歸一化4 階中心矩。峭度是無量綱參數，定義為

包絡譜熵計算公式為

式中：（ρ1，ρ2，…，ρn）為包絡譜信號的幅值概率密度。

由于峭度對沖擊信號特別敏感，通常作為早期故障信號的篩選指標。另外，包絡譜熵用于衡量嚴重故障情況下信號的周期性特征。綜合峭度、包絡譜熵分別對早期故障、嚴重故障更加敏感的特點，本文提出了峭度-包絡譜熵，定義為

周期性沖擊信號是齒輪局部故障的主要特征，SKE既考慮了峭度對于沖擊特征的敏感性，也考慮了包絡譜熵對于周期信號的敏感性，σ 用于平衡兩者的變化率。當σ ＜1 時，SKE隨著周期性沖擊分量的增強而逐漸增加。

2 方法流程

基于DEVMD方法的直升機行星輪系故障監測方法流程如下。

①采用加速度傳感器采集原始振動信號。

②采用OGS算法進行前置降噪。

③基于DEVMD方法對故障敏感信號進行提取。

a.采用DEVMD方法對信號進行模態分解，得到BIMF分量。

b.從分解的BIMF分量1 ～K 中提取故障敏感信號分量。

④對提取的故障敏感信號分量進行包絡譜分析。

⑤提取SKE故障指示因子進行故障監測。

⑥輸出故障監測結果。

3 實驗驗證

3.1 實驗設計

實驗采用直升機行星輪系實驗平臺采集的樣本數據進行驗證，采用安裝在齒圈殼體處的加速度傳感器進行信號采集，采樣頻率為10 kHz，如圖2 所示。故障模式涵蓋正常狀態和3 種不同裂紋長度的故障狀態，如圖3 所示。

圖2 直升機行星輪系實驗平臺

圖3 正常狀態與3種不同裂紋長度的故障狀態

3.2 實驗結果分析

3.2.1 基于OGS算法的前置降噪效果評估

信號降噪前后波形如圖4 所示。由圖4 中的消噪效果可見，默認閾值降噪與全局閾值降噪在消除噪聲的同時也大幅削減了高頻信號，保留了低頻信號；高頻系數降噪利用尺度向量與閾值向量對高頻系數進行閾值處理后重構降噪，在消除噪聲的同時也削減了信號幅值。相比小波閾值降噪，信號通過OGS算法進行前置降噪后，大幅值的沖擊信號更加突出，小幅值且分散的信號得到了收縮，降低了信號中噪聲的幅值，整體提高了信噪比。

圖4 信號降噪前后波形

為了定量評價本文方法的降噪效果，采用信噪比（Signal-to-Noise Ratio，SNR）與均方根誤差（Root-Mean Square Error，RMSE）作為評價指標，結果如表1所示。由表1 可見，與小波各閾值降噪方法相比，OGS算法降噪SNR最大，RMSE 最小，說明基于OGS算法的前置降噪更適用于這種具有成組稀疏特性的信號形式，其對噪聲的濾除和對原有信號的保持效果更優。

表1 OGS算法與小波各閾值降噪效果對比

3.2.2 基于DEVMD 方法的故障敏感信號分量提取效果評估

對OGS 算法前置降噪后的信號進行DEVMD 分解，根據經驗值，帶寬因子δ選擇為5 倍太陽輪旋轉頻率，采用滑動平均功率譜密度極值點確定的模態數量K為5，中心頻率｛｝＝｛5fib，fm，2fm，3fm，fsr｝。圖5 分別為故障狀態（太陽輪齒根裂紋）下，DEVMD 分解的各BIMF分量的頻譜分布。由圖5 可見，DEVMD方法準確地將信號分解為以主要齒輪部件的嚙合頻率或其倍頻為中心頻率的調制信號分量，中心頻率分別為輸入錐齒輪旋轉頻率5 倍頻、行星傳動輪系嚙合頻率及其2 倍頻、3 倍頻和二級減速齒輪嚙合頻率。由此可見，DEVMD方法有效地將各齒輪部件嚙合振動形成的模態信號進行了分離，消除了齒輪部件嚙合振動信號之間的耦合干擾，有利于單獨對各齒輪部件的健康狀態進行識別。

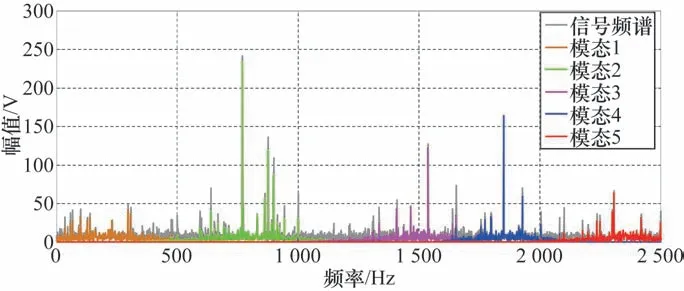
圖5 故障狀態下各模態分量的頻譜分布

故障狀態下，用DEVMD 方法將信號分解為主旋翼軸、輸入錐齒輪、液壓泵傳動齒輪等各旋轉頻率及倍頻成分組成的BIMF分量1、行星傳動輪系一階嚙合頻率及其邊頻成分組成的BIMF分量2、行星傳動輪系二階嚙合頻率及其邊頻成分組成的BIMF分量3、二級減速齒輪一階嚙合頻率及其邊頻成分組成的BIMF分量4、行星傳動輪系三階嚙合頻率及其邊頻成分組成的BIMF分量5，如圖6 所示。

圖6 故障狀態下用DEVMD方法分解的BIMF分量

3.2.3 基于峭度-包絡譜熵的故障監測效果評估

按照故障敏感信號分量提取準則，從BIMF 分量中提取中心頻率分別為行星傳動輪系嚙合頻率、其2倍頻和3 倍頻的BIMF信號分量2、分量3 與分量5 作為故障敏感信號分量，故障模式下各故障敏感信號分量的沖擊成分幅值相比正常模式均有所增強。故障敏感信號分量在正常狀態與故障狀態下的包絡譜如圖7所示，與正常狀態相比，故障狀態下包絡譜中主要峰值譜線的幅值出現了較大幅度的增強，說明了行星傳動輪系齒輪故障的存在。

圖7 故障敏感信號分量的包絡譜

計算正常狀態與不同故障狀態下故障敏感信號分量的SKE，如表2 所示。由表2 可見，在所有故障敏感信號分量中，BIMF分量2 的SKE在故障狀態下最大，且與正常狀態相比變化最大，不同裂紋長度對應的SKE不同，且隨著故障程度增加（裂紋長度增大），SKE相應增大，從而實現故障監測。

表2 故障敏感信號分量的SKE

3.3 實驗結果對比

將本文方法與對比方法，即組合小波閾值濾波、EMD方法信號分解和歸一化峭度值作為故障指示因子的故障監測方法進行對比，如圖8 所示。由圖8 可見，本文方法的故障指示因子在正常與故障狀態下幅度變化的指示性和對應不同故障程度的趨勢性都優于對比方法，體現了實驗方法在直升機行星傳動輪系故障監測中的優異性能。

圖8 DEVMD與對比方法的實驗結果

4 結束語

針對直升機行星輪系復雜信號背景下故障特征的提取難題，提出了一種新的直升機行星輪系故障監測方法，該方法首先集成了OGS算法作為前置濾波對背景噪聲進行抑制，然后通過DEVMD 方法對濾波信號進行分解并提取故障敏感信號分量，最后從故障敏感信號分量中提取SKE作為故障指示因子，實現了對直升機行星傳動輪系的故障監測。采用直升機行星傳動輪系實驗平臺的正常狀態與3 種不同故障程度狀態進行了本文方法的效果評估，并將評估結果與常用的其他方法進行了對比，驗證了本文方法的有效性，解決了復雜信號背景下直升機行星輪系的故障監測難題。