基于學生立場的學習材料選擇
——以“帶余除法”一課為例

浙江省金華師范學校附屬小學 陳鋒平

數學教學中的選材既要符合學生的年齡特點和思維現狀，更要有利于學生對知識的理解感知和歸納提升。現筆者就“帶余除法”不同的片段設計，做對比分析。

一、基于學生的想法準備學習材料

教學“帶余除法”時，教師一般會從整除過渡到有余除法，下面兩組材料是教學中教師經常選擇的：

材料A:擺一個正方形用4 根小棒，8 根小棒可以擺幾個這樣的正方形？9 根呢？

材料B:把6 顆糖平均分在3 個盤子中，每盤里有幾顆糖？把7 顆糖平均分在3 個盤子中呢？

乍一看這兩組材料，似乎沒有什么差別。但如果從學生思考的過程出發，兩組材料的差別便出現了：材料A 用9 根同樣的小棒拼正方形，學生的第一想法是拼了2 個正方形，但拼第3 個正方形還少3 根；教師引導學生用算式表示：9÷4=2（個）……1（根）。這組材料對學生來說是還少幾根小棒而不是多了幾根小棒。這里的余1 根是要從還少3 根轉個彎回來的。教師讓學生增加小棒根數繼續拼，當用11 根小棒拼時，拼成了2 個正方形，但拼第3 個正方形還少1 根，列式為11÷4=2（個）……3（根），這時感覺就更明顯了，需要把缺少3 根轉化為剩余1 根。因此，通過這組材料的學習，學生感受更多的是“想到少了幾根小棒，而不是多了幾根小棒”。

如果讓學生使用材料B，把7 顆糖平均分在3 個盤子中，每盤2 顆，還剩1 顆，7÷3=2（顆）……1（顆），學生的理解是分了6 顆糖后還多了1 顆，這1 顆自然就是多余的。材料A 和材料B 本質上的區別是體現少還是多的問題，教師在選材的時候應該基于學生的想法進行材料的選擇和準備，才能幫助學生通過嘗試、交流、比較、分析等活動自主去探索、去發現，建構新的知識結構。

二、貼近學生的感覺準備學習材料

下面繼續對比分析分糖和裝乒乓球兩組材料。

材料A:把8 顆糖平均分在3 個盤子中，每盤里有幾顆糖？把7 顆糖平均分在3 個盤子中呢？

材料B:有12 個乒乓球，每6 個裝一盒，能裝幾盒？13 個乒乓球呢？14 個呢？……

如果選用材料A，當把8 顆糖等分到3 個盤子中時，列式8÷3=2（顆）……2（顆），每盤分到2 顆，余下也是2 顆，商和余數都是2，單位也一致，“余”的感覺不明顯。如果選用材料B，當把14 個乒乓球每6 個裝一盒，能裝幾盒？還余幾個？列式14÷6=2（盒）……2（個），盡管商和余數都是2，但因為單位不一樣，商是2 盒，余數是2 個，2 盒給學生的感覺就是“整的”，2 個給學生的感覺就是“余下”的。所以，“分糖”與“裝乒乓球”對比，裝乒乓球更利于學生感受到帶余除法中商和余數的區別。

要想數學學習材料凸顯“數學味”，教師應盡量選擇貼近學生感覺的學習材料。通過對這樣的學習材料展開思考和研究，數學學習過程就會變得更容易理解，數學學習也會變得更生動。

三、有利于學生的提煉準備材料

材料A:

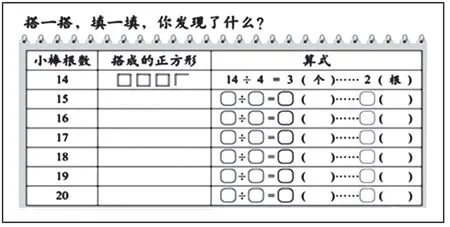
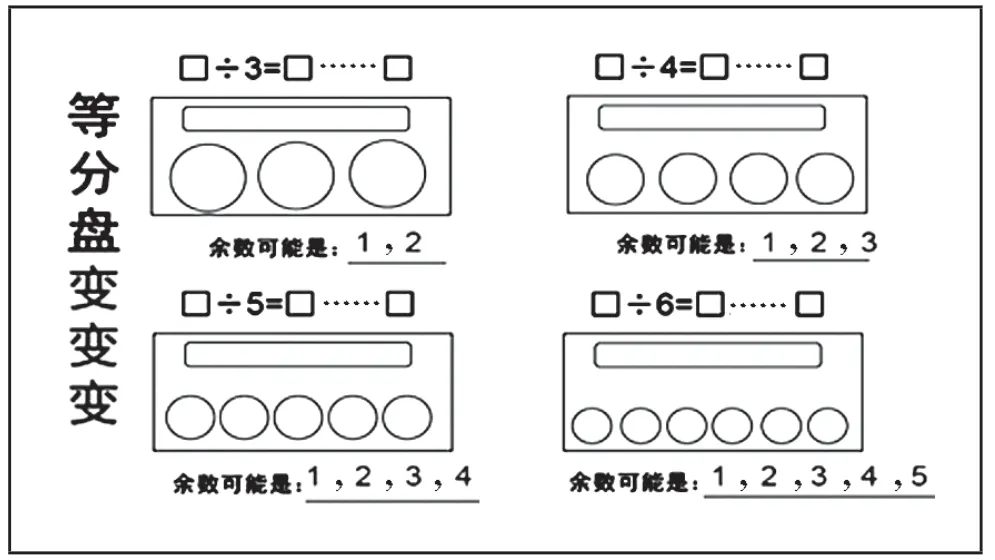
材料B:

材料A 用一組算式來研究余數的特點，會受兩個因素的干擾，一是如果將呈現的算式逐一計算，需要花很多時間，如果不計算呢，學生心里又不踏實。如果再出現一組除數是4 的算式進行比較，計算量就更大了。二是通過觀察算式，學生往往得到的是余數的變化規律，比如說平均分在3 個盤子中，余數會出現余1，2，0，1，2，0，…這一周期性的變化，很少有學生會把除數和余數進行對比。

材料B 沒有具體的除法算式，也沒有出現余數的周期變化了，算式中只出現一個除數，學生能更專注地觀察和思考余數只是和除數相關。以分糖為例，當把一堆糖平均分在3 個盤子中時，可能余下的是幾顆呢？學生根據生活常識很容易明白不可能余下3 顆及以上的，因為還能再分。這時教師可以追問：如果把一堆糖平均分在4 個盤子中時，可能余下的是幾顆呢？平分在10 個盤子中呢？……這樣學生很容易明白余數一定比除數小，而不會把注意力放在余數的變化規律上。因此，是用算式組“找規律”，還是通過“等分盤變變變”來思考，哪個材料更有利于學生概括總結出“余數一定比除數小”，我們就選哪個材料。

數學是思維的體操。在選擇學習材料的時候，教師應以學生的思維為突破口，用富有思考價值的問題和富有積極意義的操作，激活、發展學生的思維，使學生通過嘗試、交流、比較、分析等活動自主去探索、去發現，建構新的知識結構。

四、為學生更能明白準備材料

下面兩組關于分糖的材料只有細微的差別，材料A 的算式中，商和余數寫上了單位，材料B 中的沒有寫，但它們在對幫助學生的理解方面卻差別很大。

材料A:

12÷3=4（人）

13÷3=4（人）……1（塊）

14÷3=4（人）……2（塊）

15÷3=5（人）

16÷3=5（人）……1（塊）

17÷3=5（人）……2（塊）

18÷3=6（人）

19÷3=6（人）……1（塊）

20÷3=6（人）……2（塊）

21÷3=7（人）

（1）提問：觀察算式，有什么發現？

（2）追問：為什么余數是1 或2？有可能是3 嗎？

材料B:

12÷3=4

13÷3=4……1

14÷3=4……2

15÷3=5

16÷3=5……1

17÷3=5……2

18÷3=6

19÷3=6……1

20÷3=6……2

21÷3=7

（1）提問：觀察算式，有什么發現？

（2）追問：為什么余數是1 或2？有可能是3 嗎？

上面兩份材料是同一位教師在說課和上課時的不同處理，如果直接省略商和余數的單位，看起來似乎簡潔了，但其實不利于學生理解余數的意義。材料A 中13 塊糖，每人分3 塊，可以分給幾個人？還剩余幾塊？列式為13÷3=4（人）……1（塊），分給4 個“人”，余下1“塊”糖，所以選擇更能讓學生明白的材料很重要。

數學教學中所選的材料要凸顯數學學科知識的本質。所選的學習材料與教學目標要有針對性，教師在教學過程中要充分挖掘每個材料的價值及它們之間的關聯，從而讓學生真正把握教學內容的數學實質。