基于模型預(yù)測的AUV 軌跡跟蹤滑模控制方法

黃浩乾，鄭康健，馬驚天

（河海大學(xué) 能源與電氣學(xué)院，南京 211100）

欠驅(qū)動自主水下航行器（Autonomous Underwater Vehicle,AUV）精確跟蹤能力是水下探測、救援和特殊水下任務(wù)的技術(shù)基礎(chǔ)[1]。欠驅(qū)動AUV 是一種獨(dú)立控制輸入小于運(yùn)動自由度數(shù)的AUV，與全驅(qū)動AUV 相比，它在降低系統(tǒng)能耗、成本和質(zhì)量、提高系統(tǒng)可靠性方面更有優(yōu)勢，因此在工程實(shí)踐[2]中得到了廣泛應(yīng)用。欠驅(qū)動AUV 的運(yùn)動方程具有非線性、耦合、水動力參數(shù)時變和外界干擾等特點(diǎn)，增加了運(yùn)動控制的難度[3]。因此，欠驅(qū)動AUV 的軌跡跟蹤問題已成為研究熱點(diǎn)[4]。目前用于欠驅(qū)動AUV 軌跡跟蹤控制算法的主要有滑模控制[5]、反步控制[6]、自適應(yīng)控制[7]和模型預(yù)測控制[8]等。滑模控制結(jié)構(gòu)簡單，魯棒性強(qiáng)，常用于欠驅(qū)動AUV 軌跡跟蹤。為了解決狀態(tài)和控制輸入量化影響下的潛在量化問題，通過對滑模控制的有關(guān)項(xiàng)增加量化誤差的界，提出了一種軌跡跟蹤控制律。反步法在軌跡跟蹤控制中也很常見，因?yàn)樗梢越档拖到y(tǒng)的復(fù)雜性。文獻(xiàn)[9]利用滑模技術(shù)對系統(tǒng)參數(shù)變化的不敏感特性，將無抖振滑模控制器應(yīng)用到AUV 上，獲得較好的跟蹤控制效果，但外界擾動未作考慮，且不能保證系統(tǒng)自適應(yīng)估計項(xiàng)的有界性。為了克服不確定性、未知參數(shù)和外界干擾對系統(tǒng)的影響，彭玉東[10]提出了一種新的反演控制結(jié)構(gòu)，主要針對AUV 懸停問題，但沒有考慮軌跡跟蹤問題。自適應(yīng)控制對系統(tǒng)參數(shù)的變化具有較強(qiáng)的適應(yīng)能力，并具有較強(qiáng)的抵抗外界干擾的能力，因此常與其他控制方法結(jié)合使用，以消除外界干擾，增強(qiáng)系統(tǒng)的魯棒性[11]。Qiu 等通過構(gòu)造自適應(yīng)滑模控制律實(shí)現(xiàn)了模型參數(shù)不確定情況下的軌跡跟蹤控制[12]，但沒有考慮輸出最優(yōu)化，提高計算利用率問題。而在實(shí)際AUV 應(yīng)用中，推力限制、安全工作區(qū)域等系統(tǒng)約束是不可避免的，因此在設(shè)計跟蹤控制器時需要考慮這些約束。

模型預(yù)測控制（Model Predictive Control,MPC）是一種基于優(yōu)化的時域控制方法[13]，在處理多約束、多變量和不確定控制問題方面具有良好性能，為解決控制問題提供了一個強(qiáng)大的控制框架[14,15]。2017 年，Shen 等提出了一種用于AUV 平面軌跡規(guī)劃與跟蹤的編隊(duì)控制方案，并給出了跟蹤控制[16]穩(wěn)定條件。2018年，Gan 等提出了一種基于量子粒子群優(yōu)化（Quantum-behavioral Particle Swarm Optimization,QPSO）模型的無人潛航器（Unmanned Underwater Vehicle,UUV）三維軌跡跟蹤控制預(yù)測控制算法，并考慮了滑模控制對系統(tǒng)參數(shù)變化和擾動的不敏感性，綜合應(yīng)用。但是，求解開環(huán)最優(yōu)控制問題會帶來計算量。隨著問題規(guī)模的增加，計算復(fù)雜度呈指數(shù)級增長。為了解決MPC 的計算復(fù)雜度，采用了數(shù)值延拓、事件觸發(fā)控制[17]和離線預(yù)計算等策略。對于AUV 的跟蹤控制，由于所要求的軌跡具有時變特性，需要找到更好的解決方案。另一種旨在降低非線性模型預(yù)測控制（Nonlinear Model Predictive Control,NMPC）在線計算負(fù)荷的策略。通過將六自由度動力學(xué)方程分解為三個相互作用較小的子系統(tǒng)，可實(shí)現(xiàn)分布式求解。然而，由于MPC 通過求解優(yōu)化問題來確定控制信號，控制信號是系統(tǒng)狀態(tài)的隱函數(shù)，給分析閉環(huán)穩(wěn)定性帶來了巨大的挑戰(zhàn)，特別是對于AUV 等非線性系統(tǒng)。然而，如前所述，局部線性化不適用于AUV 軌跡跟蹤。

綜上所述，目前基于MPC 控制的AUV 軌跡跟蹤存在以下三個問題：（1）在海流干擾和模型參數(shù)不確定情況下AUV 跟蹤軌跡誤差較大；（2）標(biāo)準(zhǔn)MPC 設(shè)計需要對所制定的優(yōu)化問題使用終端約束，并通過局部線性化構(gòu)造相應(yīng)的輔助穩(wěn)定控制律，然而，局部線性化并不適用于AUV 軌跡跟蹤；（3）在AUV 運(yùn)動過程中，會有執(zhí)行器飽和與抖震的問題，從而不能確保系統(tǒng)的穩(wěn)定性。針對上述問題，本文提出一種基于滑模輔助控制器同模型預(yù)測控制相結(jié)合的方法，解決欠驅(qū)動AUV 軌跡跟蹤問題。主要貢獻(xiàn)如下：

（1）針對在海流干擾和模型參數(shù)不確定情況下AUV 跟蹤軌跡問題，設(shè)計滑模控制算法，利用滾動優(yōu)化和反饋校正補(bǔ)償不確定項(xiàng)和海流干擾的影響；

（2）針對MPC 算法局部線性化問題，提出滑模與模型預(yù)測控制相結(jié)合的方法，能夠處理系統(tǒng)動力約束問題，避免MPC 局部線性化問題；

（3）針對執(zhí)行器飽和與輸出抖震問題，設(shè)計滑模控制器作為輔助控制器，在解決執(zhí)行器飽和的同時，還能避免系統(tǒng)抖震，從而確保系統(tǒng)的穩(wěn)定性。

1 問題描述

為研究AUV 的運(yùn)動軌跡，將6 自由度AUV 運(yùn)動分解為3 自由度（縱蕩、橫蕩、艏搖）的AUV 的水平運(yùn)動。欠驅(qū)動AUV 模型具體如圖1 所示。

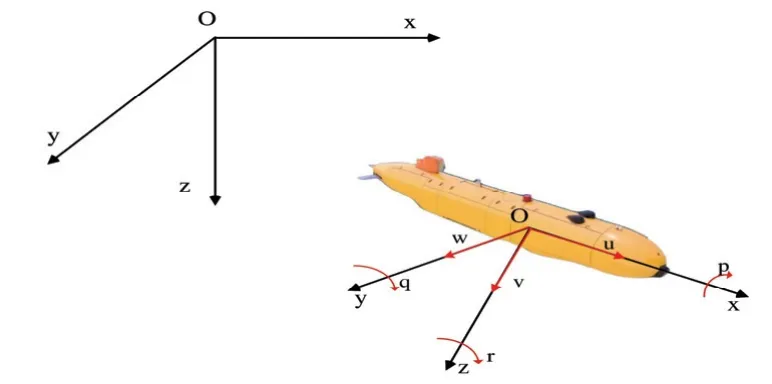
圖1 AUV 模型Fig.1 AUV model

忽略縱搖、橫搖和垂蕩相對應(yīng)的變量，運(yùn)動學(xué)方程如式(1)所示：

其中，η=[x,y,Ψ]T表示位置向量p=[x,y]T和方向Ψ，式(1)中為η導(dǎo)數(shù)；v=[u,v,r]T表示AUV 速度向量；J(Ψ)表示旋轉(zhuǎn)矩陣，如式(2)所示：

運(yùn)動學(xué)與AUV 靜止或勻速行駛時的平衡有關(guān)，而動力學(xué)與AUV 加速運(yùn)動有關(guān)。3 自由度非線性動力學(xué)運(yùn)動方程可以方便地表示為：

其中，M為系統(tǒng)慣性矩陣，C(v)表示科里奧向心矩陣，D(v)表示阻尼矩陣，g(η)表示恢復(fù)力矩陣，τ表示控制輸入，d表示擾動。

令τω=d-g(η)，將式(1)與式(3)結(jié)合，可以建立新的AUV 跟蹤問題系統(tǒng)模型：

將x=[x,y,Ψ,u,v,r]T定義為新的狀態(tài)變量，τ=[τu,τv,τr]T定義為新的控制變量。為更加直觀的展示AUV 各狀態(tài)變量之間的關(guān)聯(lián)關(guān)系，將式(4)展開為以下形式：

AUV 模型的以下特性推導(dǎo)較為容易，并在控制器設(shè)計中加以應(yīng)用。

特性1：初始矩陣是對稱正定且有上界：0＜M=MT≤＜ ∞(其中I 為3 階單位矩陣)；

特性2：科里奧向心矩陣是反對稱矩陣：-C(v) =C(v)T；

特性3：旋轉(zhuǎn)矩陣的逆矩陣滿足以下特性：J-1(Ψ) =J(Ψ)，并且滿足表示二范數(shù)）；

特性4 ：阻尼矩陣是正定矩陣：D(v) ＞0；

其中atan2 表示四象限正切逆算子。則式(3)可寫為：

2 基于Lyapunov 模型預(yù)測軌跡跟蹤控制器設(shè)計

在本文考慮模型不確定和存在干擾的場景中，AUV 可以跟蹤預(yù)定軌跡，并且在設(shè)計的控制器作用下，可精準(zhǔn)地跟蹤預(yù)定軌跡，從而達(dá)到想要的效果。

控制器原理框圖如圖2 所示，共包含三部分：AUV、輔助控制率、MPC 控制器；其中輔助控制率可以生成局部AUV 的穩(wěn)定性約束，即計算約束MPC 優(yōu)化問題的最優(yōu)輸入。

圖2 AUV 軌跡跟蹤原理圖Fig.2 Schematic diagram of AUV trajectory tracking

2.1 輔助控制率設(shè)計

為了構(gòu)造收縮約束，需要找到一個狀態(tài)反饋控制器以及相應(yīng)的Lyapunov 函數(shù)。針對AUV 軌跡跟蹤問題，利用反步法設(shè)計基于Lyapunov 的非線性滑模控制器。η=[x,y,Ψ]T表示 AUV 的實(shí)際軌跡，ηr=[xr,yr,Ψr]T表示期望軌跡，定義以下變量變換：

可以將v看作一個虛擬控制，從而得到：

令α1=，代入式(15)(16)得：

選取一個Lyapunov 函數(shù)：

其中Κp=ΚpT＞0，對V1求導(dǎo)得：

為使V2正定，選取以下控制率：

利用非線性滑模輔助控制器的幫助構(gòu)造收縮約束，由于滑模項(xiàng)的引入，控制輸入會出現(xiàn)不連續(xù)性，從而導(dǎo)致抖振問題。在這里采用一種具有動態(tài)邊界層的飽和函數(shù)sat 代替符號函數(shù)sign，引入邊界層會導(dǎo)致穩(wěn)態(tài)誤差，影響系統(tǒng)穩(wěn)定性。這里通過調(diào)整邊界層厚度，使其隨著狀態(tài)軌跡的收斂而逐漸收縮，最終與切換平面重合來減少系統(tǒng)輸出抖振并保證系統(tǒng)的漸進(jìn)穩(wěn)定性。首先引入接近角概念，接近角λ是系統(tǒng)狀態(tài)軌跡與切換平面之間的夾角，會隨著狀態(tài)軌跡接近切換平面而不斷減小。通過λ來描述狀態(tài)變量收斂的程度，并以此設(shè)計邊界層厚度函數(shù)μ(λ) =tan(λ)。基于該邊界層厚度函數(shù)可以得到動態(tài)邊界層的飽和函數(shù)：

最終設(shè)計的控制器為：

那么，可以建立AUV 軌跡跟蹤控制的直觀MPC約束如式(27)-(30)所示：

其中，x(s)為預(yù)測控制，τ(s)的預(yù)測狀態(tài)軌跡，利用系統(tǒng)模型從x(t0)演化而來為誤差狀態(tài)；為控制誤差；S(δ)為以采樣周期δ為特征的分段常數(shù)函數(shù)，T=Nδ為預(yù)測區(qū)間；權(quán)重矩陣Q、P、R都是正定的。但眾所周知，由于預(yù)測界有限解的最優(yōu)性不能自動保證閉環(huán)穩(wěn)定性。為了遵循這一重要的閉環(huán)特性，需要進(jìn)行復(fù)雜的離線設(shè)計。對于AUV等非線性系統(tǒng)，采用標(biāo)準(zhǔn)MPC 設(shè)計技術(shù)，需要進(jìn)行局部線性化，以選擇合適的加權(quán)矩陣并構(gòu)造輔助的局部反饋控制律。此外，如引言所述，對于AUV 跟蹤曲線參考局部線性化是不合適的。

為避免局部線性化，同時保證MPC 跟蹤控制的閉環(huán)穩(wěn)定性，設(shè)計滑模控制的輔助非線性跟蹤控制律，并通過在原MPC 公式中添加收縮約束來解決滑模模型預(yù)測控制（Silding Model Predictive Control,SMPC）問題。

其中h(?)為輔助的基于Lyapunov 的非線性跟蹤控制律，V(?)為對應(yīng)的Lyapunov 函數(shù)。收縮約束式(35)的存在能夠證明SMPC 控制器繼承了狀態(tài)反饋控制h(x)的穩(wěn)定性屬性。此外，由于在線優(yōu)化過程，SMPC控制器將自動執(zhí)行最好的跟蹤控制。

基于SMPC 控制器的軌跡跟蹤控制將以遞減的方式實(shí)現(xiàn)，控制算法總結(jié)在算法1 中。

遞歸的可行性和閉環(huán)的穩(wěn)定性都不依賴于優(yōu)化的精確解。在算法1 中，次優(yōu)解是完全可以接受的，這對于任何非線性MPC 算法都是非常可取的。由于系統(tǒng)動力學(xué)是非線性的，使用迭代方法，式(34)最佳保證解是局部最優(yōu)解。更重要的是，在計算資源有限的嵌入式系統(tǒng)上實(shí)現(xiàn)時，迭代次數(shù)可能會受到實(shí)時控制的限制。換句話說，實(shí)時控制與次優(yōu)解的兼容性限制了數(shù)值效率和控制性能之間的靈活性。可以在不破壞跟蹤控制的情況下，通過指定最大迭代次數(shù)來輕松地進(jìn)行權(quán)衡。

因此，收縮約束式(35)的詳細(xì)表達(dá)式為：

2.2 穩(wěn)定性分析

為了證明MPC 的穩(wěn)定性，此處定義V3(k)為Lyapunov 函數(shù)，即：

二次函數(shù)恒大于0，因此正定性得證，即：

再證明V3(K+1) ≤V3(K)即可證明其穩(wěn)定。

因此V3(k+1) ≤V3(k)，穩(wěn)定性得以證明。

3 實(shí)驗(yàn)結(jié)果

在本節(jié)中，通過建立兩個對比仿真實(shí)驗(yàn)來驗(yàn)證SMPC 算法在AUV 系統(tǒng)中進(jìn)行軌跡跟蹤的有效性。第一種情況是不存在外部干擾的情況下，對AUV 的軌跡跟蹤進(jìn)行了測試。第二種情況是存在參數(shù)未知且有干擾的情況下，通過引入未知參數(shù)和干擾來測試系統(tǒng)的魯棒性。仿真結(jié)果表明，該方法具有良好的跟蹤性能和魯棒性。

3.1 參數(shù)選擇

參考軌跡為正弦曲線，具體如下：

對于SMPC 算法的控制器，使用以下參數(shù)：采樣周期δ=0.1s，預(yù)測范圍T=5δ,權(quán)重系數(shù)設(shè)為Q=diag(105,105,103,102,102,102)，P=diag(103,103,102,10,10,10)，R=diag(10-2,10-2,10-2)，每個輸出區(qū)間為[-400,400],控制增益為Κp=Κd=diag(5,5,5)，初始條件為

3.2 仿真結(jié)果與分析

（1）軌跡跟蹤實(shí)驗(yàn)

在SMPC 控制器的作用下，具體的跟蹤效果如圖3 和圖4 所示，其中黑色的曲線為參考軌跡曲線，紅色的曲線為在SMPC 控制器作用下AUV 運(yùn)動軌跡曲線，藍(lán)色曲線為基于反步法的滑模控制器（Sliding Controller,SC）下的運(yùn)動軌跡。

圖3 參數(shù)已知且無干擾軌跡跟蹤Fig.3 Track tracking with known parameters and no disturbance

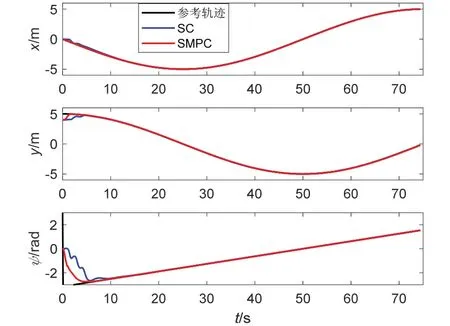
圖4 參數(shù)已知且無干擾下各位置跟蹤圖Fig.4 Location tracking with known parameters and no disturbance

從圖3 可知，相較于SC 控制器，在SMPC 控制器的作用下AUV 可以更為準(zhǔn)確快速地跟蹤參考軌跡，并且追蹤效果更好，充分驗(yàn)證了閉環(huán)的穩(wěn)定性。同時，仿真結(jié)果驗(yàn)證了提出SMPC 控制算法的有效性。具體無干擾情況下均方誤差（Mean Square Error,MSE）如表1 中所示，所提方法均方誤差較SC 提升60%以上。

表1 無干擾情況下兩種算法均方差Tab.1 Mean square error of two algorithms without interference

每個推進(jìn)器所需的推力如圖5 所示，可以看出，在跟蹤剛開始時，SMPC 控制器使用的推力接近極限值，以便進(jìn)行最快的收斂，而SC 控制器則超出規(guī)定的最大推力，且跟蹤效果不如SMPC 控制器。整體而言，SMPC 控制器控制輸出的大小始終保持在預(yù)期的允許范圍內(nèi)，并達(dá)到最快的跟蹤效果。采用滑模模型預(yù)測控制計算出的控制輸出對于實(shí)際系統(tǒng)而言也是可行的，并且可以快速收斂至預(yù)定軌跡。

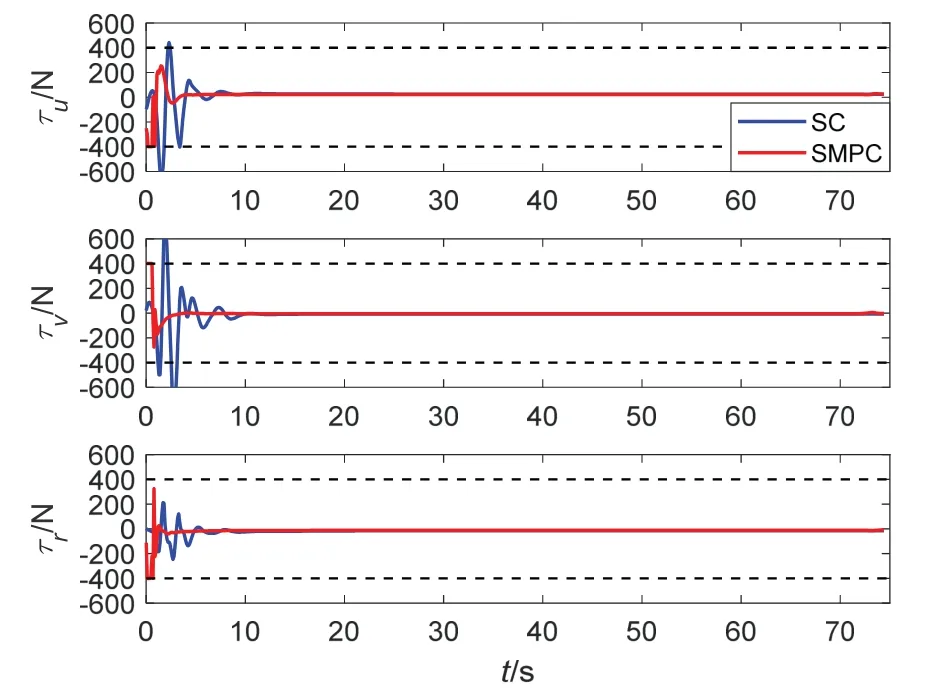
圖5 參數(shù)已知且無干擾下系統(tǒng)輸出Fig.5 System output with known parameters and no disturbance

（2）魯棒性實(shí)驗(yàn)

滑模控制和模型預(yù)測控制通過反饋引入到閉環(huán)系統(tǒng)中，從而使得SMPC 控制擁有極強(qiáng)的魯棒性和抗干擾能力，為了測試魯棒性，對魯棒性跟蹤控制進(jìn)行了研究。為了證明SMPC 的跟蹤控制：引入模型恢復(fù)力參數(shù)（未知且有界）和洋流擾動。在仿真過程中，模擬海洋擾動與不確定參數(shù)范圍τω?[ -1 00,100]。

在圖6 所示的仿真結(jié)果中，對比普通的SC 控制器，可以發(fā)現(xiàn)基于SMPC 的跟蹤控制仍然能使AUV較快地收斂至期望的軌跡，證明所提出算法具有較強(qiáng)的魯棒性和抗干擾能力。通過圖7 可以看出，即使在存在干擾的情況下，AUV 控制輸出的大小始終保持在預(yù)期的允許范圍內(nèi)，但在SC 控制器作用下，AUV 推力大小超出規(guī)定范圍。從而進(jìn)一步驗(yàn)證了所提算法的穩(wěn)定性。

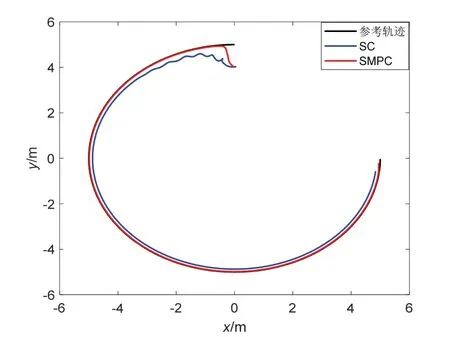
圖6 參數(shù)未知且有干擾軌跡跟蹤Fig.6 Unknown parameters and disturbance trajectory tracking

圖7 參數(shù)未知且有干擾系統(tǒng)輸出Fig.7 Unknown parameters and disturbance system output

圖8 參數(shù)未知且有干擾各位置跟蹤圖Fig.8 Tracking diagram of each position with unknown parameters and disturbance

通過以上兩個仿真可以看出，本文提出的SMPC算法在模型參數(shù)不確定和干擾情況下都具有良好性能，在跟蹤實(shí)驗(yàn)中，SMPC 算法控制的AUV 可以快速跟蹤軌跡。在魯棒性實(shí)驗(yàn)中，雖然存在一定誤差，但是在SMPC 的作用下，AUV 可以利用在線優(yōu)化來調(diào)度適當(dāng)?shù)目刂圃鲆鎭硌a(bǔ)償干擾和參數(shù)不確定帶來的影響。因此，SMPC 控制顯著提高了軌跡跟蹤控制的魯棒性和穩(wěn)定性，如表2 所示，在有干擾情況下與SC算法相比均方誤差明顯提升。

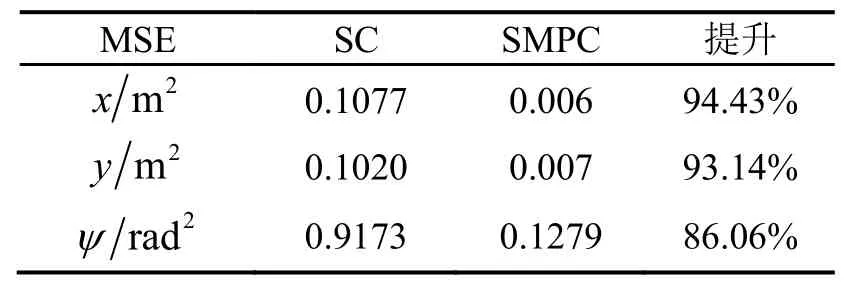
表2 有干擾情況下兩種算法均方差Tab.2 Mean square error of two algorithms under interference

4 總結(jié)

在復(fù)雜的水下環(huán)境中，AUV 軌跡跟蹤普遍存在海洋干擾、參數(shù)不確定等問題。本文從3 自由度AUV出發(fā)，根據(jù)以上問題提出一種用于AUV 軌跡跟蹤的SMPC 控制算法。在滑模輔助控制器基礎(chǔ)上，加入了在線優(yōu)化，從而極大提升了控制性能和魯棒性，并基于李雅普諾夫穩(wěn)定性定理證明了整個閉環(huán)跟蹤系統(tǒng)的穩(wěn)定性，最終將本論文設(shè)計控制器應(yīng)用于欠驅(qū)動AUV進(jìn)行軌跡跟蹤仿真實(shí)驗(yàn)，結(jié)果表明，本文所設(shè)計控制器具有較高的跟蹤精度和較強(qiáng)的魯棒性。

文中軌跡跟蹤是在無障礙物的情況下進(jìn)行的，而實(shí)際水下環(huán)境復(fù)雜，會導(dǎo)致AUV 與障礙物發(fā)生碰撞，因此未來會考慮在AUV 碰撞情況下，對系統(tǒng)設(shè)計相應(yīng)的控制器，今后將結(jié)合不同的控制器進(jìn)一步研究避碰情況下的軌跡跟蹤，以實(shí)現(xiàn)系統(tǒng)的精確控制。