匯流排型材在重力作用下最大撓度與其截面參數關系探討

張學明，王春娟，嚴仁杰，暢 明，豆 雯

0 引言

電氣化鐵路剛性懸掛接觸網匯流排是剛性接觸網中用于夾持固定接觸線，并靠其自身的剛性保持接觸線的恒定位置，使接觸線不因重力而產生弛度的部件[1-3]。剛性接觸網中所用的匯流排一般由鋁合金制成，其質量檢驗所依據的行業標準為TB/T 3252—2022。在該標準的出廠試驗項目中，對匯流排型材有最大撓度方面的要求。一般而言，型材的最大撓度與材料彈性模量、截面形狀、型材長度、所受彎矩等因素有關。下文將通過求解型材的撓度曲線方程，討論該類型材最大撓度的影響因素及其控制方法。

1 建立力學模型

一般而言，如果對型材在重力作用下有撓度要求，往往會規定一個合適的跨距，在該跨距內，型材相應位置的撓度應滿足一定要求。為方便描述，繪制如圖1 所示力學模型，并在圖1 中建立直角坐標系xow，設型材長度為l，用于檢測撓度的2 個支撐點位置分別設為（l1，0）和（l2，0），型材單位長度質量為m，則支撐點間距（跨距）為l2-l1，單位長度的重力為mg（g為重力加速度，其值為9.8 m/s2）。

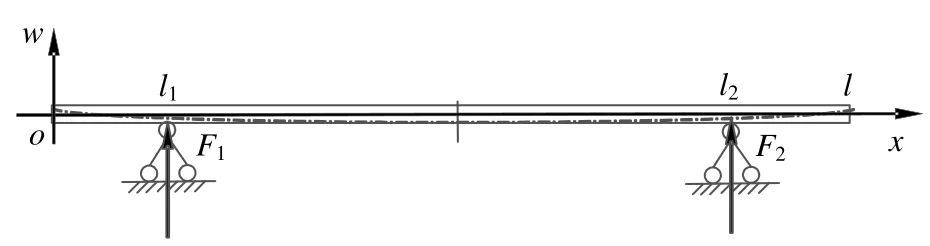
圖1 力學模型

由靜力學平衡條件可知：

對于支點關于中軸線對稱分布的情況，有l=l1+l2，此時式（1）、式（2）可化簡為

式（1）、式（2）比式（3）更具一般性，但用其推導出的方程十分復雜，且在型材撓度測量中一般不使用該方程，故本文不作討論，如遇到此類情況，可直接求出F1和F2的具體數值，并用下文所述方法代入求解即可。本文只討論式（3）的情況。

根據圖1 所建立的直角坐標系及式（3），由端面法易知剪力方程為

需注意的是，支撐點處有集中力F1、F2，剪力方程不連續。

由材料力學可知，彎矩與剪力有如下關系：

將式（4）代入式（5），并由圖1 可知，無集中力偶作用時彎矩不發生突變，為連續函數，且M(0) =M(l) = 0，故彎矩方程為

2 求解撓曲線方程

根據材料力學知識，撓曲線近似微分方程為[4]

式中：w為撓度；E為彈性模量（又稱楊氏模量）；I為截面對中性面的慣性矩。

對式（7）進行一次積分，可得轉角方程為

將式（6）代入式（8），轉角方程為

對式（7）進行二次積分，可得撓度方程為

將式（6）代入式（10），可得

根據圖1 及撓度光滑連續條件得邊界條件為

將式（12）代入式（9）及式（11），并由撓度光滑連續條件可得積分常數為

3 問題討論

依據TB/T 3252—2022 的第6.8 條，剛性懸掛接觸網匯流排的撓度測量方法為：在專用平臺上用4 個特制的可調高度的錐形墊腳將12 m 匯流排墊起，匯流排兩端各用2 個錐形墊腳；錐形墊腳的支點距離型材端頭50 mm，調節4 個墊腳水平，用高度游標卡尺量得型材兩端最大高度與匯流排中部最小高度的差值[5]。根據該標準要求，可確定l1= 50 mm，l2= 11 950 mm，l= 12 000 mm；再根據匯流排截面形狀及尺寸，利用CAD 軟件計算其截面對中性面（即xoy面，其中x軸過o點且垂直于截面）的慣性矩I= 3 403 543.47 mm4。匯流排截面如圖2所示。

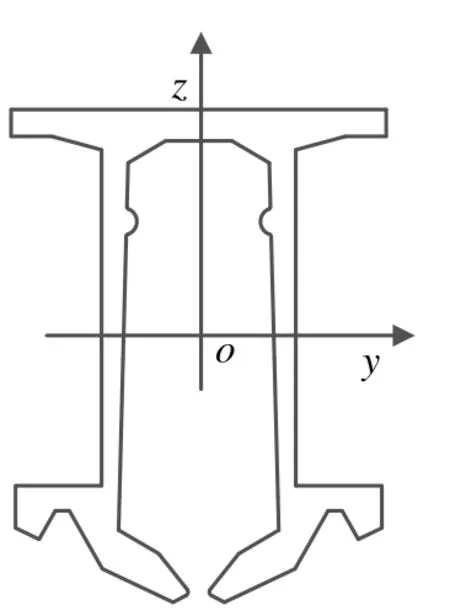
圖2 匯流排截面

需注意的是，利用CAD 軟件計算截面慣性矩時，不能直接求解，須先確定型材截面的形心，并將系統坐標系原點設置于型材截面的形心處。圖2中yoz坐標系原點o即為匯流排型材截面的形心。

經計算可以得到型材的截面積A= 2 235.02 mm2。一般電氣化鐵路剛性懸掛接觸網所用匯流排為6101B（T6）鋁合金，在室溫下其對應的彈性模量為69 000 N/mm2。考慮到其密度約為2.7 g/cm3，則該截面的匯流排單位長度質量m= 2.7×10-3×2 235.02 g/mm = 6.03 g/mm = 6.03 kg/m。

綜上所述，式（11）中涉及的所有參數均可計算得到，如表1 所示。

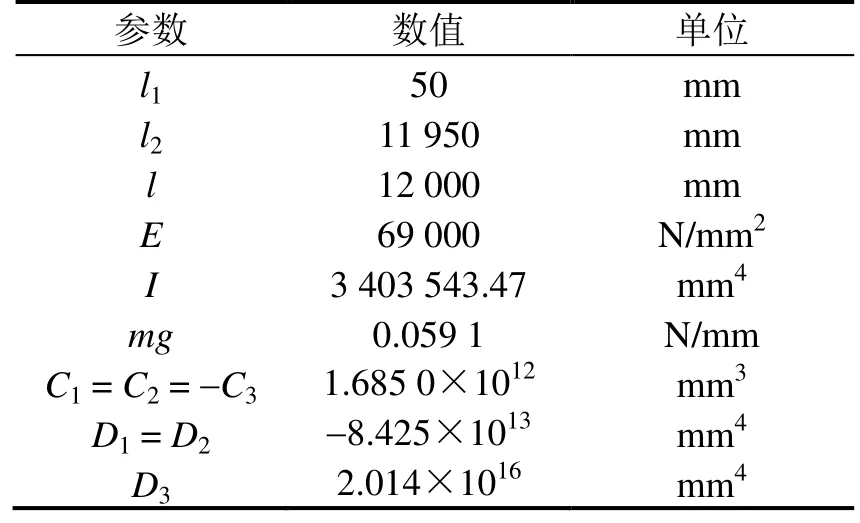
表1 匯流排撓度方程參數

將表1 中的數據代入式（11），可得匯流排在TB/T 3252—2022 第6.8 條要求下試驗時的撓度方程為

圖3 匯流排撓度曲線（單位：mm）

以上撓度方程及撓度曲線是根據理論計算得出的，表2 是對10 根不同批次、規格為12 m、截面為圖2 所示的匯流排，嚴格依據TB/T 3252—2022 的第6.8 條要求測量的最大撓度實測值。

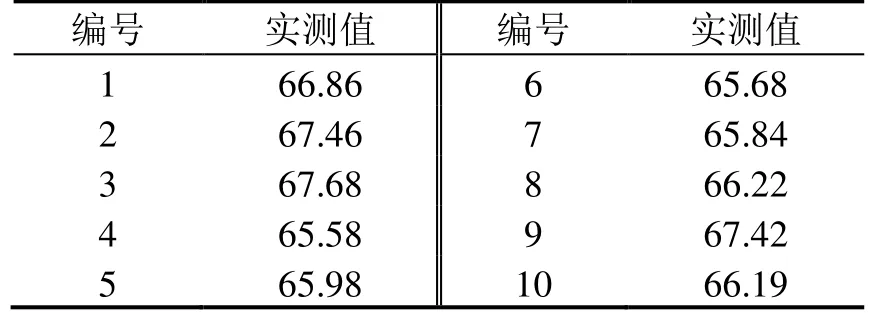
表2 匯流排撓度實測值 mm

結合理論計算結果，從表2 可以看出，匯流排最大撓度的實測值與理論值相差不大。查閱相關資料可知，材料的彈性模量是材料抵抗彈性變形的一個量，是材料剛度的一個指標，其與材料的化學成分和溫度有關，與組織變化無關，熱處理對其影響不大，約為±5%左右[6]。從式（11）可以看出，型材在重力作用下的撓度與彈性模量成反比關系，考慮到熱處理對彈性模量的微小影響，匯流排的理論最大撓度范圍區間為(66.58×95%, 66.58×105%) =(63.25, 69.91)，而TB/T 3252—2022 的表2 匯流排性能參數中要求最大撓度wmax≤70 mm，若考慮到型材加工誤差等其他因素的影響，有可能會導致匯流排型材的撓度不能滿足不大于70 mm 的要求。從式（11）可以看出，在型材材質一定、檢測方式一定（即型材長度、支撐點位置一定），并考慮到熱處理對彈性模量有±5%影響后，影響型材最大撓度的因素只有截面慣性矩和單位長度質量。

下文討論能否通過增加截面積的方法減小型材在重力作用下最大撓度。增加型材截面積意味著型材單位長度質量m也隨之增加，從式（11）可以看出，最大撓度與m和I的比值成正比，而m=ρA，ρ為型材體密度，A為截面積。因此，最大撓度與A和I的比值成正比，即

式中：α為引入的比例系數，mm3；積分區域為型材截面輪廓圍成的區域。對于不同的截面形狀，A/I一般也不同，當增加截面積時，若A/I隨之增大，則無法通過該方式減小型材在重力作用下的最大撓度，若A/I隨之減小，則可以通過該方式減小型材在重力作用下的最大撓度。但是，通過這種方式調整型材自重下的最大撓度時，由于A和I均增大，型材撓度的理論值減小效果并不明顯，同時也會增大型材單位長度的重量，經濟性較差。

綜上所述，減小型材在自重作用下最大撓度比較合理的方案是：在滿足載荷和安裝要求的情況下，保證型材截面積不增加（即保持不變或減小），同時使型材截面的材料盡量遠離中性面，以增大型材對中性面的慣性矩I。

以圖2 為例，TB/T 3252—2022 第5.2.2 條規定了鉗口尺寸，這是用于夾持接觸線的關鍵尺寸，不能隨意變更。對除此之外的其余尺寸，在不影響現場安裝并滿足載荷要求的情況下，可以盡量使之遠離xoy平面。如果不考慮其他因素，對圖2 匯流排截面的頂部尺寸增加1 mm，同時各壁厚保持不變，此時，計算型材截面的截面積及慣性矩分別為A=2 210.93 mm2，I= 3 417 492.22 mm4，與圖2 相比，截面積有所減小，慣性矩有所增加。此時m=ρA=5.97 kg/m。將I及m代入式（11），并利用表1 的其他數據，可計算出w(x)m=w(6 000) = -64.70 mm，w(0) =w(12 000) = 0.87 mm。最大撓度wmax=w(0)-w(x)m= 65.57 mm。考慮到熱處理對E有±5%的影響，此時，匯流排的理論最大撓度范圍區間為(62.29, 68.84)，即使考慮制造誤差，撓度的理論值仍有一定的裕度，可以滿足TB/T 3252—2022 表2中最大撓度不大于70 mm 的要求。

對于有撓度要求的型材，理論上可根據式（17）確定其截面幾何參數。例如，型材在某段距離支撐點下的最大撓度應滿足wm≤[w]，[w]為允許最大撓度，即

式中：α為引入的比例系數，mm3。從式（11）可以確定只要型材的材質一定（即E、ρ一定），撓度的測量條件一定（即l、l1、C2、D2一定），則α即為定值。式（19）可作為滿足型材撓度要求的充分必要條件。對于截面形狀規則的型材而言，可以通過式（19）準確計算出其截面尺寸的臨界值，如為圓形截面，可以求出最小直徑。但對于形狀不規則的截面，由于（截面坐標系為yoz，原點為截面形心），積分區域為型材截面輪廓圍成的區域，很難通過函數關系準確表達，一般無法找到截面尺寸需要滿足的臨界條件，但可以借助軟件求解A/I的具體數值，然后代入式（19），反向驗證設計的截面尺寸是否滿足撓度要求。

4 結語

型材在重力作用下的撓度是表征型材抵抗彎曲變形的重要指標，通過分析可知，若考慮熱處理對材料彈性模量的影響，本文所述截面形式的匯流排通過理論計算出的撓度值非常接近標準值。對于此類情況，建議在不增加截面積的前提下，可以適當改變型材材料的分布情況。本文推導出的撓曲線方程可用于一般型材在重力作用下最大撓度的校驗，也可用于確定某些形狀規則簡單截面的臨界尺寸。對于有熱處理要求的型材，如果技術標準中或實際工況中對型材撓度的控制要求較高，設計型材截面時還應考慮5%的彈性模量變化。