直流區域配電系統小信號穩定性分析研究

呂 飛，王 冕，趙豐剛

（海軍士官學校，安徽蚌埠 233012）

0 引言

在電力電子領域中，綜合電力系統是最具有代表性的研究方向，其成為未來艦船電力及動力系統發展的趨勢。直流區域配電系統作為艦船綜合電力系統的重要部分，其穩定性是首要考慮的問題。直流區域配電系統中，由于非線性電力電子變換器負載相互連接，必然會涉及到各種電力電子變換器模塊的并聯、串聯和級聯，并且為了減弱模塊的高頻紋波干擾，需要在電力電子變換器的輸入端口和母線連接上濾波器。另外由于在組建直流區域配電系統、系統故障和系統擴容時，不穩定可能導致整個系統的癱瘓[1-7]，因此有必要對系統穩定性問題作充分的認識和分析。

直流區域配電系統不穩定情況包含兩種：小信號穩定性和大信號穩定性。小信號穩定性，是指在工作點附近的小信號分析。考慮到電力電子模塊的非線性特點，其不滿足疊加原理，也不能對系統的阻抗比實施離線測量。同時，系統的穩定性是相對于工作點的，不一樣的工作點的穩定性不同，在啟動、運行及關機等過程中，系統要經過多個不同的工作點，這些不同點工作的穩定要求是系統在較大信號干擾下的穩定性研究問題。本文主要研究較小信號上的不穩定問題，研究的穩定性問題也都是小信號意義上的穩定性問題。

直流區域配電系統的小信號不穩定問題的原因：雖然單獨設計的電力電子變換器自身是較穩定的，但是由于變換器間的相互關聯作用，以及變換器各模塊與濾波器之間的相互關聯作用，可能會使得電力電力系統出現不穩定。

1 直流區域配電系統穩定性分析

典型的直流區域配電系統如圖1 所示。

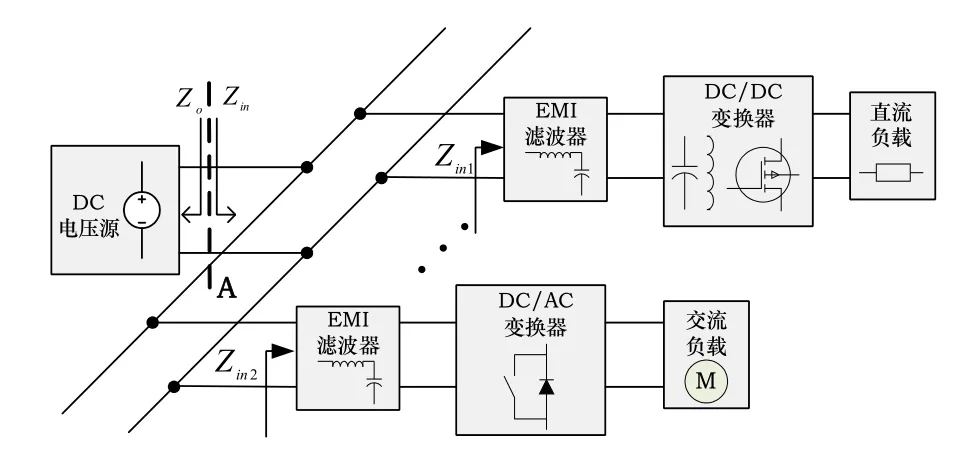
圖1 典型直流區域配電系統

圖1 所示，直流區域配電系統中存在輸入濾波器與DC/DC 變換器，輸入濾波器與DC/AC 變換器以及AC/DC 變換器與DC/DC 變換器(中間存在EMI 濾波器)等模塊間的連接。由于模塊之間的相互作用，可能引起振蕩，導致系統不穩定[8]。

對于各種電力電子變流器而言，在理想情況下，輸入功率等于輸出功率，當輸入電壓增加時，輸入電流減小，所以其輸入阻抗一般呈負阻特性。系統發生不穩定的主要原因就是因為變流器的負阻特性與輸入源的阻抗特性不相匹配，近而相互之間作用，使得系統出現不穩定問題。

DC/DC Buck 變流器是常用的電力電子變換器，在理想狀態下分析，如圖2 所示為帶輸入濾波器的DC/DC Buck 變流器在靜態工作點附近的等效電路，可見，DC/DC Buck 變換器可以用一個電阻(Rin)來近似表示。則有：

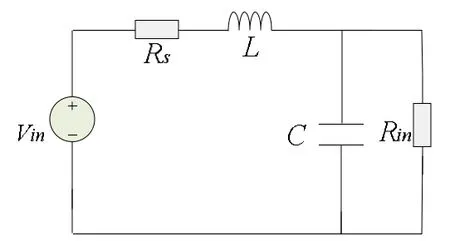
圖2 帶輸入濾波器的BUCK 等效電路

式（1）中Vin、Iin分別代表系統工作的電壓和電流的直流分量，vin、iin分別代表系統工作的電壓和電流的交流分量。由于小信號的二次項可以不計，則得到輸入阻抗為：

u為輸出端電壓，其對輸入端電壓的擾動量為vin，如下式：

由式（3）可見，對輸入電壓的擾動（vin），經過濾波器后，其輸出電壓（u）可能產生大幅度的振蕩，這就是不穩定的一種情況。

2 流區域配電系統穩定性Middle brook阻抗分析

對整個系統進行仿真是對直流區域配電系統穩定性驗證的最直接也是最常用的方法，但是仿真分析法僅能對具體系統進行穩定性驗證，并不能從理論上給出系統的穩定性指導[9]。

直流區域配電系統小信號穩定性的分析方法較多，其中Middlebrook 阻抗分析法使用較為廣泛。阻抗分析法最初用來分析濾波器和后級開關變流器的相互作用引起的不穩定情況，現在廣泛應用于判別復雜系統的穩定性。

Middlebrook 最先從阻抗角度分析電力電子系統穩定性的并形成了Middlebrook 阻抗標準。如圖3 所示，設模塊1 和模塊2 的電壓傳遞函數分別為Av1(s)、Av2(s)，模塊1 的輸出阻抗為Zo(s)，模塊 2 的輸入阻抗為Zin(s)，設Tm(s) =Zo(s)/Zin(s)。則有：

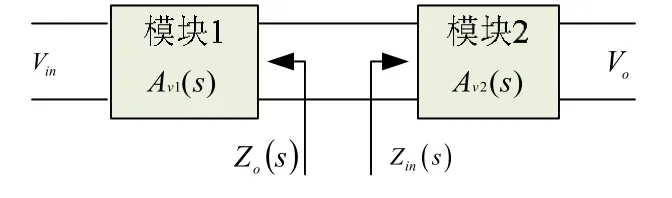
圖3 兩個電力模塊的連接

式（4）中，1 +Tm(s)代表子系統連接后的負載效應，Tm(s)可以看作系統的等效環路增益。系統的穩定性分析，可采用Nyquist 穩定性定理進行分析，即Tm(s)在復平面上不包含(-1,j0)點。

傳遞函數中，1 +Tm(s)為串聯的兩個子系統的負載及源效應。Tm(s)為整個系統的環路增益。由于子系統是穩定的，則能根據Tm(s)的穩定性來判斷整個系統的穩定性，也就是Tm(s)滿足Nyquist 穩定性判定定理，則整個系統穩定；如果Tm(s)不滿足Nyquist 穩定性判定定理，則整個系統不穩定，這就是Middlebrook 阻抗分析法的標準。由此，直流區域配電系統的穩定性研究，可轉化為研究子系統輸入、輸出特性的問題。相較與其他的穩定性的分析方法，Middle brook 阻抗分析標準具有明顯的優點，它不需要掌握子系統的內部參數，也不需要對整個系統建模，可以只分析子系統的輸入特性和輸出特性，更適合工程設計。

在實際應用中，系統開環基本都是穩定的。整個系統的穩定性研究，可以依據環路增益Tm(s)能否包括復平面點(-1,j0)進行判斷。如果環路增益Tm(s)應不包圍復平面點(-1,j0)，則系統是穩定的，反之，系統是不穩定的。同時，Tm(s)的曲線與復平面點(-1，j0)的越靠近，則系統的穩定性越好。

等效環路增益Tm(s)符合Nyquist 穩定性判定標準的充分條件是Middlebrook 阻抗分析法的標準，即所有頻率條件內，||Tm(s)||＜ ＜ 1，也就是，在所有頻率條件內，前一級子系統的輸出阻抗一定要遠小于后一級子系統的輸入阻抗。可見，只要滿足Middle brook 阻抗分析法的標準，可滿足整個系統的穩定性條件，并且使得系統輸入及輸出的動態特性進行了隔離，即輸入端的效應對后級系統的整體性能沒有影響。

3 直流區域配電系統禁止區穩定性分析

Middle brook 阻抗標準非常嚴格，要滿足穩定條件，整個系統設計會變得非常保守,在實際應用中，系統的穩定性較難滿足。考慮到設計容易，同時，滿足系統穩定性要求的阻抗標準，可采取禁止區的穩定性分析方法。禁止區就是在極坐標圖中設定一塊區域，只要等效環路增益不進入這個區域，認為系統就穩定，而且基本具有系統穩定要求的增益裕度及相位裕度。

為確保整個系統的增益裕度GM 和相位裕度α，對于環路增益Tm(s)，禁止區的穩定性分析法認為只要Tm(s)的極坐標圖不進入如圖4所示的禁止區內，系統是穩定的，而且基本具有系統穩定要求的增益裕度及相位裕度。假定系統的整個輸出阻抗己知，根據圖4 所示禁止區，對負載端的輸入阻抗的要求為:

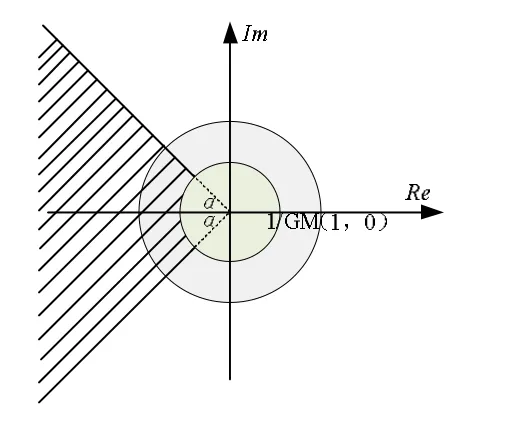
圖4 禁止區穩定性分析

對輸入阻抗而言，它的幅值下限就是:

由式（7）可得，禁止區穩定性分析法根據已知的輸出阻抗對輸入阻抗的約束顯然要比Middlebrook 阻抗標準容易滿足。

對于多個模塊組成的系統，其輸入阻抗和輸出阻抗分別是整個系統中所有子系統模塊的輸入阻抗和輸出阻抗的之和。

對多模塊系統，其輸入阻抗為：

這樣，等效環路增益Tm 可以表示為：

等效環路增益Tm 可以認為是許多個單個負載模塊和源模塊之間的等效環路增益的總和。

可見，一個簡單的禁止區往往具有大的保守性，對負載阻抗的定義簡單，也容易測量和判別系統的穩定性，但大的保守性增加了設計的成本和復雜性；相反,一個復雜的禁止區不保守，但是不易用來測量和判別系

統的穩定性。總之禁止區是保守性和簡單性的折衷，要根據實際情況選擇合適的禁止區，即便于使用又最大程度上減小保守性對設計的影響。

4 結論

電力電子模塊的集成技術作為電力電子技術的一個重要發展方向。而綜合電力系統是電力電子領域最具有代表性的研究方向。直流區域配電系統作為艦船綜合電力系統的重要部分，其穩定性是首要考慮的問題。本文分析了分布式直流區域配電系統不穩定的原因，在級聯系統的穩定性研究中，一般采用阻抗分析的方法進行研究，詳細分析了運用Middlebrook 阻抗標準進行穩定性分析的方法，同時指出由于Middlebrook 阻抗分析方法的要求過于嚴格，其保守性會給系統設計帶來一些不利的影響。于是又引用了禁止區穩定性分析法，對直流區域配電系統穩定性設計有一定參考意義。