“大概念”引領(lǐng)下數(shù)學(xué)解題教學(xué)的實(shí)踐與思考
——以“一類導(dǎo)數(shù)恒成立問(wèn)題的策略”為例
程建新, 田 闊
(1.杭州市余杭中學(xué),浙江 杭州 311121;2.浙江省蔡小雄名師工作室,浙江 杭州 310000)
《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》指出,進(jìn)一步精選學(xué)科內(nèi)容,重視以學(xué)科大概念為核心,使課程內(nèi)容結(jié)構(gòu)化,以主題為引領(lǐng),使課程內(nèi)容情境化,促進(jìn)學(xué)科核心素養(yǎng)的落實(shí).可以看出,學(xué)科大概念在新課程、新高考的實(shí)施中占有十分重要的地位.圍繞大概念的研究目前主要集中在基于大概念理解的單元整體教學(xué)設(shè)計(jì),而基于大概念視角的解題及解題教學(xué)的探索還很少[1].
劉徽教授指出,大概念是將素養(yǎng)落實(shí)到具體教學(xué)中的錨點(diǎn),是指反映專家思維方式的概念、觀念或論題,具有生活價(jià)值.理解大概念有助于形成高通路遷移,形成具體與抽象的復(fù)雜認(rèn)知結(jié)構(gòu).大概念的理解不僅可以讓學(xué)生通過(guò)掌握少而精的內(nèi)容,形成結(jié)構(gòu)化的知識(shí)網(wǎng)絡(luò),在真實(shí)情境中建構(gòu)大概念,從而提升獨(dú)立且真實(shí)地解決問(wèn)題的能力,還可以在遷移應(yīng)用中內(nèi)化大概念,對(duì)提升學(xué)生的核心素養(yǎng)具有重要意義.
在高三的復(fù)習(xí)備考過(guò)程中,學(xué)生需要經(jīng)歷各個(gè)單元的系統(tǒng)復(fù)習(xí),對(duì)所學(xué)知識(shí)進(jìn)行二次加工,在提升解題思維方面狠下功夫.因此,教師需要引導(dǎo)學(xué)生回歸原點(diǎn),將相關(guān)聯(lián)的知識(shí)和方法進(jìn)行歸類、整合,以“大概念”引領(lǐng)高三的深度復(fù)習(xí),幫助學(xué)生形成豐富的知識(shí)網(wǎng)絡(luò)和解題方法體系.筆者開(kāi)設(shè)了一節(jié)“一類導(dǎo)數(shù)恒成立問(wèn)題的策略”的高三復(fù)習(xí)課,下面以這節(jié)課為例展開(kāi)說(shuō)明.
1 提取大概念,明確學(xué)習(xí)目標(biāo)
為了獲取“利用導(dǎo)數(shù)解決恒成立問(wèn)題”的大概念,需要站在整個(gè)“函數(shù)”與“導(dǎo)數(shù)”單元的高度對(duì)教學(xué)內(nèi)容進(jìn)行剖析.從課程標(biāo)準(zhǔn)的角度定位,函數(shù)是描述客觀世界變化規(guī)律的重要數(shù)學(xué)模型.從函數(shù)基本性質(zhì)的研究,再到冪函數(shù)、指數(shù)函數(shù)、對(duì)數(shù)函數(shù)、三角函數(shù),一類一類地研究這些基本初等函數(shù),對(duì)每一類函數(shù),都由圖象到性質(zhì)、由性質(zhì)到圖象地進(jìn)行研究.“導(dǎo)數(shù)”單元是對(duì)函數(shù)性質(zhì)和基本初等函數(shù)的進(jìn)一步深化研究,利用“導(dǎo)數(shù)”這一工具,定量地研究函數(shù)的局部性質(zhì)(如極值點(diǎn)、最值點(diǎn)、零點(diǎn)等).因此,研究重心還是“函數(shù)”,“函數(shù)的基本性質(zhì)”和“回歸原點(diǎn)”的解題理念是本節(jié)課的大概念.
恒成立問(wèn)題是學(xué)生從高一就接觸的一類典型問(wèn)題.學(xué)生對(duì)處理恒成立問(wèn)題的兩種基本方法(最值分類討論法和參變分離法)已經(jīng)很熟悉,而導(dǎo)數(shù)中的恒成立問(wèn)題是新高考考查的重點(diǎn)與難點(diǎn)之一,學(xué)生對(duì)于“導(dǎo)數(shù)”工具還是稍感陌生,對(duì)求導(dǎo)的目的不清,很多時(shí)候,學(xué)生只知道求導(dǎo),但是卻不知道求導(dǎo)是為了什么,難以回歸到導(dǎo)數(shù)單元的大概念原點(diǎn)——函數(shù).
2 導(dǎo)數(shù)中恒成立策略探究的問(wèn)題設(shè)計(jì)
2.1 創(chuàng)設(shè)情境,激發(fā)興趣
本節(jié)課以一道高考導(dǎo)數(shù)題為例:
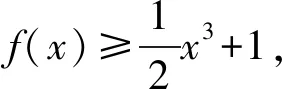
(2020年全國(guó)數(shù)學(xué)高考Ⅰ卷理科試題第21題節(jié)選)
問(wèn)題1這是一道函數(shù)恒成立問(wèn)題,你認(rèn)為有哪些方法可以解決這類問(wèn)題?
生1:參變分離.
師:請(qǐng)用參變分離嘗試解決,在解決過(guò)程中你遇到了哪些困難?
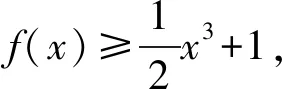


師:還有其他方法嗎?

最后轉(zhuǎn)化為求函數(shù)
的最大值,難點(diǎn)在于涉及參數(shù)范圍的討論,比較煩瑣.
師:導(dǎo)數(shù)是研究函數(shù)局部性質(zhì)的工具,我們能否通過(guò)觀察函數(shù)的局部特征為參數(shù)范圍探路呢?這是本節(jié)課要研究的內(nèi)容.
2.2 問(wèn)題引領(lǐng),探究生成
2.2.1 探路手段1:端點(diǎn)效應(yīng),端點(diǎn)代入
例2已知函數(shù)f(x)=(x+1)lnx-a(x-1),當(dāng)x∈(1,+∞)時(shí),f(x)>0,求實(shí)數(shù)a的取值范圍.
(2016年全國(guó)數(shù)學(xué)高考新課標(biāo)Ⅱ卷文科試題第20題節(jié)選)
問(wèn)題2請(qǐng)觀察不等式右邊的值與函數(shù)值的關(guān)系,你發(fā)現(xiàn)了什么特征?
生4:當(dāng)x=1時(shí),f(1)=0,即f(x)>0=f(1),剛好在端點(diǎn)處取到.
師:這說(shuō)明函數(shù)f(x)在x=1附近的小鄰域內(nèi)具有什么特征?
生5:說(shuō)明函數(shù)f(x)在x=1附近的小鄰域內(nèi)一定會(huì)呈現(xiàn)單調(diào)遞增的趨勢(shì).
師:為什么會(huì)呈現(xiàn)局部遞增的趨勢(shì)呢?
生6:因?yàn)槿绻鹒(x)在x=1附近的小鄰域(1-δ,1+δ)(其中δ>0)內(nèi)遞減,那么f(x) 師:函數(shù)f(x)在x=1附近的小鄰域內(nèi)單調(diào)遞增,如何用數(shù)學(xué)語(yǔ)言進(jìn)行刻畫(huà)? 生7:f(x)在x=1處的導(dǎo)函數(shù)f′(x)≥0. 師:那么這個(gè)參數(shù)a的范圍a≤2是否就是最終要求的范圍呢? 生8:應(yīng)該是的. 師:a≤2這個(gè)范圍只是一個(gè)必要條件,下面我們把a(bǔ)≤2當(dāng)作已知條件,來(lái)證明充分性. 當(dāng)a≤2時(shí), f(x)=(x+1)lnx-a(x-1) ≥(x+1)lnx-2(x-1). 接下來(lái)證明(x+1)lnx-2(x-1)>0即可.將對(duì)數(shù)單獨(dú)分離出來(lái)進(jìn)行考慮,由于 只需證明 從而g(x)在區(qū)間(1,+∞)上單調(diào)遞增,即 g(x)>g(1)=0, 于是當(dāng)a≤2時(shí),f(x)>0. 當(dāng)a>2時(shí),直接考察函數(shù)f(x)的單調(diào)性,因?yàn)?/p> 所以f′(x)在區(qū)間(1,+∞)上單調(diào)遞增,且 根據(jù)零點(diǎn)存在定理,可知存在x0∈(1,+∞),使得f′(x0)=0,函數(shù)f(x)在區(qū)間(1,x0)上單調(diào)遞減,在區(qū)間(x0,+∞)上單調(diào)遞增,則 f(x0) 與已知f(x)>0矛盾,故充分性不成立. 設(shè)計(jì)意圖通過(guò)問(wèn)題鏈的設(shè)計(jì),引導(dǎo)學(xué)生觀察函數(shù)的端點(diǎn)值,回歸函數(shù)與導(dǎo)數(shù)的大概念:函數(shù),從而得到命題成立的必要條件,在此基礎(chǔ)上再證明充分性.該方法稱為“端點(diǎn)效應(yīng)”,本質(zhì)是利用導(dǎo)數(shù)定量地刻畫(huà)函數(shù)在局部鄰域內(nèi)的單調(diào)性,同時(shí)也為分類討論提供了分類的“界點(diǎn)”. 2.2.2 探路手段2:端點(diǎn)效應(yīng),局部恒成立 (2011年全國(guó)數(shù)學(xué)高考新課標(biāo)卷理科試題第21題節(jié)選) 問(wèn)題3你認(rèn)為用參變分離的方法,可行嗎? 生9:參變分離,得 求極值點(diǎn)非常煩瑣. 問(wèn)題4能否直接移項(xiàng)構(gòu)造函數(shù),觀察端點(diǎn)值有何特征? 生10:移項(xiàng)得到 師:我們不妨將自變量范圍限定在x∈(1,+∞),則問(wèn)題可以轉(zhuǎn)化為 恒成立,利用端點(diǎn)效應(yīng)可以得到什么? 故 k≤0. 師:下證充分性.當(dāng)k≤0時(shí), 從而當(dāng)x∈(1,+∞)時(shí), h(x) 當(dāng)x∈(0,1)時(shí), h(x)>h(1)=0, 則 命題得證. 當(dāng)k>0時(shí),不等式不恒成立,請(qǐng)同學(xué)們自行證明,此處不再贅述. 設(shè)計(jì)意圖通過(guò)該問(wèn)題的設(shè)計(jì),引導(dǎo)學(xué)生深刻理解導(dǎo)數(shù)是定量地研究函數(shù)局部性質(zhì)的工具,將問(wèn)題轉(zhuǎn)化為導(dǎo)函數(shù)在局部小鄰域內(nèi)的恒成立問(wèn)題,從而得到命題成立的必要條件,在此基礎(chǔ)上再證明充分性. 2.2.3 探路手段3:極值點(diǎn)效應(yīng) 例4已知函數(shù)f(x)=ex-1-x-ax2,當(dāng)a≥0時(shí),f(x)≥0,求實(shí)數(shù)a的取值范圍. (2010年全國(guó)數(shù)學(xué)高考新課標(biāo)卷理科試題第21題節(jié)選) 問(wèn)題5還可以類似例2和例3,通過(guò)代入端點(diǎn)值求解嗎? 生12:我們注意到f(0)=0,即f(x)≥f(0),于是得到f′(0)≥0,但是f′(x)=ex-1-2ax,f′(0)=0,最后a消失了,得不到a的范圍. 師:也就是剛才的“端點(diǎn)效應(yīng)”失效了,那就回歸原點(diǎn),利用導(dǎo)數(shù)去研究函數(shù)的局部性質(zhì),問(wèn)題轉(zhuǎn)化為:在區(qū)間為(0,δ)(其中δ是很小的正數(shù))的小鄰域內(nèi),f′(x)=ex-1-2ax≥0恒成立,其中f′(0)=0.你觀察到了什么? 生13:設(shè)g(x)=ex-1-2ax≥0=g(0),利用端點(diǎn)效應(yīng),得到 g′(0)=1-2a≥0, 即 師:盡管一開(kāi)始“端點(diǎn)效應(yīng)”失效了,但是我們可以通過(guò)導(dǎo)函數(shù)的端點(diǎn)效應(yīng)(極值點(diǎn)效應(yīng)),將a的范圍探出來(lái).下面證明充分性: h′(x)=ex-(x+1)≥0, 則h(x)在[0,+∞)上單調(diào)遞增,即 h(x)≥h(0)=0, 問(wèn)題6通過(guò)上述幾道例題,你能否歸納端點(diǎn)效應(yīng)或極值點(diǎn)效應(yīng)的基本特征呢? 生14:一類是端點(diǎn)函數(shù)值為0;另一類是區(qū)間端點(diǎn)函數(shù)值為0,且導(dǎo)函數(shù)的端點(diǎn)值也為0. 類型1若f(x)≥0(含參數(shù)a)在x∈[m,n]上恒成立,且f(m)=0或f(n)=0,則f′(m)≥0或f′(n)≤0. 類型2若f(x)≥0(含參數(shù)a)在x∈[m,n]上恒成立,且 則 f″(m)≥0或f″(n)≤0. 設(shè)計(jì)意圖通過(guò)函數(shù)端點(diǎn)效應(yīng)失效,引導(dǎo)學(xué)生進(jìn)一步觀察其導(dǎo)函數(shù)的端點(diǎn)值,從而將問(wèn)題轉(zhuǎn)化為導(dǎo)函數(shù)的“端點(diǎn)效應(yīng)”,即極值點(diǎn)效應(yīng). 2.3.1 探路手段4:特殊點(diǎn)效應(yīng) 例5已知函數(shù)f(x)=aex-1-lnx+lna,若f(x)≥1,求實(shí)數(shù)a的取值范圍. (2020年全國(guó)數(shù)學(xué)新高考Ⅰ卷第21題節(jié)選) 問(wèn)題7你能觀察出f(x)的端點(diǎn)函數(shù)值為1的點(diǎn)嗎? 生15:觀察不出來(lái),而且當(dāng)x趨近于端點(diǎn)時(shí),函數(shù)值不會(huì)趨近于1. 師:那能否嘗試一些特殊點(diǎn)進(jìn)行代入? 生16:因?yàn)閷?duì)任意x>0,不等式f(x)≥1都成立,而且注意到函數(shù)解析式中有l(wèi)nx,所以可以嘗試將x=1代入,得到f(1)≥0,從而a≥1. 師:a≥1只是不等式成立的必要條件,你能否嘗試證明充分性? 生17:當(dāng)a≥1時(shí), f(x)=aex-1-lnx+lna≥ex-1-lnx. 利用切線不等式ex≥x+1和lnx≤x-1,可得 f(x)≥ex-1-lnx≥x-(x-1)=1 成立,故實(shí)數(shù)a的取值范圍為a≥1. 生18:當(dāng)a≥1時(shí),可以將a當(dāng)作主元,令g(x)=ex-1·a+lna-lnx,可以發(fā)現(xiàn)g(a)在[1,+∞)上單調(diào)遞增,則 g(a)=ex-1·a+lna-lnx≥ex-1-lnx. 師:取特殊值x=1,解得a的范圍,從而縮小了a的范圍,可問(wèn)題是為什么取x=1,且當(dāng)x=1時(shí)所解得的a的范圍就是最終要求的范圍呢? 問(wèn)題8通過(guò)不等式f(x)≥1可知,如果f(x)取到最小值,那這個(gè)最小值一定是極小值,這個(gè)極小值在哪里取到呢? 生19:設(shè)f(x)在x=x0處取得最小值,于是 消元得 即 由單調(diào)性解得x0=1. 師:通過(guò)上述分析,我們知道必要性探路所取的值并不是隨意的,而是有“預(yù)謀”的,是經(jīng)過(guò)極值點(diǎn)的取值,得到相應(yīng)的特殊值代入,只是在實(shí)際過(guò)程中省略了思維過(guò)程.因此,問(wèn)題的本質(zhì)還是回歸函數(shù)的原點(diǎn),轉(zhuǎn)化為函數(shù)的極值與最值. 生20:該題還可以利用同構(gòu)進(jìn)行轉(zhuǎn)化. aex-1-lnx+lna≥1 ? ex+ln a-1+x+lna-1≥x+lnx=lnx+eln x. 令g(x)=x+ex,則 g(x+lna-1)≥g(lnx), 因?yàn)間(x)在R上單調(diào)遞增,所以 x+lna-1≥lnx, 從而 lna≥0, 即 a≥1. 設(shè)計(jì)意圖通過(guò)系列問(wèn)題的設(shè)計(jì),為學(xué)生創(chuàng)設(shè)探究的思路與空間,揭示特殊值選取背后的“原點(diǎn)”思維,讓學(xué)生理解特殊值的選取不是隨意的. (2020年全國(guó)數(shù)學(xué)高考Ⅰ卷理科試題第21題節(jié)選) 設(shè)計(jì)意圖呼應(yīng)本節(jié)課一開(kāi)始遇到的疑難問(wèn)題,讓學(xué)生嘗試?yán)锰刂堤铰吩僮C充分性.從創(chuàng)設(shè)問(wèn)題情境,到幾種探路手段的原點(diǎn)探究,最后到情境問(wèn)題的著手解決,讓學(xué)生經(jīng)歷發(fā)現(xiàn)問(wèn)題、提出問(wèn)題、分析問(wèn)題、解決問(wèn)題的探究歷程,積累在大概念引領(lǐng)下進(jìn)行數(shù)學(xué)解題的基本活動(dòng)經(jīng)驗(yàn). (2023年全國(guó)數(shù)學(xué)高考甲卷理科試題第21題節(jié)選) (2023年全國(guó)數(shù)學(xué)高考乙卷文科試題第20題節(jié)選) 設(shè)計(jì)意圖這兩道高考題都可以通過(guò)端點(diǎn)效應(yīng)和必要性探路解決,讓學(xué)生體會(huì)利用大概念進(jìn)行數(shù)學(xué)解題的“威力”. 通過(guò)以上教學(xué)案例的分析,我們發(fā)現(xiàn)函數(shù)與導(dǎo)數(shù)問(wèn)題解決的核心在于研究和利用函數(shù)的性質(zhì).研究的函數(shù)對(duì)象不一定是直接給定的形式,而是依據(jù)解題的基本活動(dòng)經(jīng)驗(yàn),通過(guò)模式識(shí)別合理選擇或改變研究對(duì)象的形式.在“導(dǎo)數(shù)是定量地研究函數(shù)局部性質(zhì)的工具”這一大概念的指引下,解題中要引導(dǎo)學(xué)生特別關(guān)注端點(diǎn)值、特殊點(diǎn)、極值點(diǎn).除此之外,筆者對(duì)高三的解題教學(xué)提出了以下3點(diǎn)建議. 高三的復(fù)習(xí)課怎么上?如何開(kāi)展高三的數(shù)學(xué)解題教學(xué)?是重新復(fù)習(xí),還是就題論題?筆者認(rèn)為,高三的復(fù)習(xí)教學(xué)既要重視基礎(chǔ)功底,也要強(qiáng)方法、講思想.如果學(xué)生的學(xué)習(xí)還是像高一、高二階段那樣停留在淺層學(xué)習(xí),就很難觸動(dòng)學(xué)習(xí)內(nèi)容的核心和本質(zhì).恒成立問(wèn)題是一個(gè)極其龐大的專題,題型多樣,解題方法豐富,但沒(méi)有一種方法可以解決所有問(wèn)題.教師提煉大概念,以大概念為引領(lǐng),幫助學(xué)生學(xué)會(huì)識(shí)別、學(xué)會(huì)轉(zhuǎn)化,建立知識(shí)與方法之間的聯(lián)系,促進(jìn)學(xué)生的深度理解,實(shí)現(xiàn)深度學(xué)習(xí)[2]. 傳統(tǒng)的高三解題教學(xué),教師一般呈現(xiàn)例題后就直接講解,提問(wèn)也缺乏系統(tǒng)性,學(xué)生很難抓住核心“大概念”.教師要以學(xué)生的數(shù)學(xué)思維為基本依據(jù),精準(zhǔn)把握學(xué)生的思維水平和思維生長(zhǎng)點(diǎn),將問(wèn)題情境進(jìn)行深度加工,設(shè)計(jì)難度合適的起點(diǎn)問(wèn)題,逐層深入、緊密關(guān)聯(lián)的過(guò)渡性問(wèn)題,具有挑戰(zhàn)性的最終問(wèn)題,以及體現(xiàn)批判性思維的發(fā)展性問(wèn)題,以問(wèn)題鏈驅(qū)動(dòng)的探究活動(dòng)將學(xué)生的思維引向深度理解[3]. 課堂教學(xué)離不開(kāi)預(yù)設(shè),但課堂的生成往往與預(yù)設(shè)有偏差.本節(jié)課的學(xué)生分享環(huán)節(jié)讓筆者有了很多意外的收獲.課堂教學(xué)是教師與學(xué)生共同完成的,是預(yù)設(shè)與生成的有機(jī)結(jié)合.深度學(xué)習(xí)的關(guān)鍵在于“學(xué)”.每名學(xué)生都有獨(dú)特的思維,對(duì)問(wèn)題分析的角度不同,對(duì)問(wèn)題也會(huì)有新的看法,特別是高三的復(fù)習(xí)課,要讓學(xué)生感到這樣的思想方法是自己想出來(lái)、悟出來(lái)的.


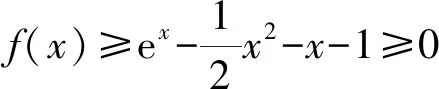
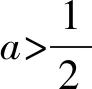

2.3 深入探究,揭示本質(zhì)
2.4 釋疑解惑,彰顯“核威力”
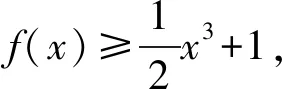
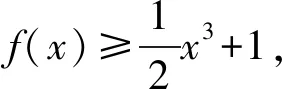


2.5 高考中的恒成立問(wèn)題
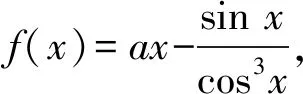
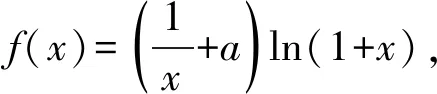
3 數(shù)學(xué)解題教學(xué)的若干教學(xué)反思
3.1 思想方法引領(lǐng),知識(shí)能力并行
3.2 以問(wèn)題鏈為抓手,引領(lǐng)深度學(xué)習(xí)
3.3 順應(yīng)學(xué)生思維,注重知識(shí)生成
 中學(xué)教研(數(shù)學(xué))2024年3期
中學(xué)教研(數(shù)學(xué))2024年3期
——以2023年全國(guó)數(shù)學(xué)新高考Ⅰ卷第6題為例
——以教材函數(shù)習(xí)題為例
——關(guān)于一道橢圓試題研析拓展的教學(xué)實(shí)錄片段
——對(duì)一道高考題的教學(xué)設(shè)計(jì)與思考
——以“平方差公式”為例
——以“單調(diào)性與最大(小)值”為例
