負剛度非線性系統(tǒng)的回復力曲面參數(shù)辨識方法
胡方圓,劉清華,曹軍義,張穎
(西安交通大學現(xiàn)代設計及轉子軸承系統(tǒng)教育部重點實驗室,710049,西安)
近幾年,負剛度結構成為了振動控制和能量俘獲領域的研究熱點[1]。隨著高精密領域對振動控制技術的要求逐漸提高,許多學者把負剛度裝置運用到隔振和能量俘獲領域中,并取得了顯著效果。其中,系統(tǒng)非線性回復力最直接反映系統(tǒng)的非線性特性,對系統(tǒng)的動力學特性的研究有很大價值。目前,國內(nèi)外學者獲取負剛度隔振器或俘能器等強非線性系統(tǒng)的非線性回復力,通常基于解析計算[2-3]、磁場仿真[4-5]或測量[6-7],再利用哈密頓原理進行系統(tǒng)的力學方程正向建模。此方法計算繁瑣、精度不高且僅適用于理想的裝配環(huán)境,尤其是會受到實驗平臺搭建后裝配條件影響,導致了非線性回復力很難精確表征。
因此,基于實驗測量的輸入、輸出數(shù)據(jù)進行非線性回復力(NRF)的逆向建模十分必要。Malatkar等利用頻譜分析辨識含立方剛度與平方剛度的非線性懸臂板系統(tǒng)[8];Vakakis等通過波特圖及奈奎斯特圖區(qū)分剛度非線性和阻尼非線性[9];Chatterjee等利用Volterra級數(shù)實現(xiàn)多項式非線性類別辨識[10];Bendat等用回復力曲面(RFS)直觀地判斷機械系統(tǒng)中常見的幾種單自由度非線性特征[11];Gondhalekar等建立了非線性頻域回復力曲線庫,實現(xiàn)了單自由度和多自由系統(tǒng)非線性類別辨識[12];Marchesiello等提出了一種子空間辨識算法來辨識三次剛度和間隙性非線性振子的回復力[13]。
非參數(shù)辨識法無需預先確定NRF的形式,在系統(tǒng)辨識的過程中得到廣泛的應用。Anastasio等利用實驗RFS來描述雙穩(wěn)態(tài)振子的剛度和阻尼力[14]。Feldman和Cohen等提出一種基于非平穩(wěn)信號振動分解的希爾伯特變換識別方法,用于識別雙穩(wěn)態(tài)電磁能量俘獲裝置的NRF[15-16]。但是,這些方法在只能從實驗中得到位移數(shù)據(jù)的情況下對噪聲很敏感,難以獲得非穩(wěn)態(tài)點附近的剛度力和保證辨識精度。
RFS法是直接利用實驗手段獲得系統(tǒng)模型中的參數(shù),無需事先確定NRF形式的純粹時域非參數(shù)辨識方法。通過濾波或數(shù)據(jù)前處理可以減少噪聲干擾,構造出真實的三維力-速度-位移曲面,可直觀地分析出系統(tǒng)的非線性特性。該方法最初由Masri和Caughey[17-18]提出,并經(jīng)Crawley等[19]加以發(fā)展和利用。其中,Kerschen等用RFS法實現(xiàn)了VTT Benchmark系統(tǒng)剛度曲線和阻尼曲線的識別研究[20]。Sun等利用RFS法識別螺栓組合梁結合部的剛度及阻尼特性參數(shù)[21]。Anastasio等基于RFS法成功解決了負剛度隔振器中摩擦的非線性辨識問題,辨識出系統(tǒng)的剛度回復力和阻尼回復力[22]。Worden等用RFS法識別在仿真計算和實驗兩種情況下分段線性的懸臂梁剛度[23],理論和實驗結果吻合較好。事實證明,RFS法可以很好地解決沒有確切解析表達式的非線性系統(tǒng)辨識問題。
RFS法的關鍵是需要通過實驗測量同時得到加速度、速度和位移。然而,由于實驗噪聲或者對實驗數(shù)據(jù)的積分和微分處理不恰當會導致相位失真,從而導致回復力面雜亂,擬合出的系統(tǒng)參數(shù)出現(xiàn)較大的辨識誤差。為解決這個問題,需要選擇有效的數(shù)據(jù)處理方法,Worden等針對地震數(shù)據(jù),對RFS法中積分和微分兩種數(shù)據(jù)處理方法進行評估及優(yōu)缺點的對比[24]。Jiang等將RFS法應用于顆粒阻尼器的研究,選擇數(shù)值積分作為數(shù)據(jù)前處理的方法[25]。但是,以上研究都對測得的加速度信號進行數(shù)值積分,會出現(xiàn)干擾趨勢項使信號偏移,而數(shù)值微分可以有效避免這種情況出現(xiàn)。目前,基于對測量位移進行微分處理且用于多穩(wěn)態(tài)負剛度振子回復力辨識的RFS法還未做過系統(tǒng)研究。
本文基于RFS法,提出一種負剛度系統(tǒng)非線性回復力的辨識方法。首先提出4種不同磁力耦合多穩(wěn)態(tài)負剛度振子回復力的構造方法,基于RFS法的辨識原理,對比研究位移微分和加速度積分的RFS數(shù)據(jù)處理方法,對4種類型多穩(wěn)態(tài)振子進行仿真研究,分析剛度力和阻尼力的辨識精度。搭建實驗臺,對不同加速度水平下的多穩(wěn)態(tài)振子進行掃頻實驗,建立多穩(wěn)態(tài)振子的回復力模型的表面,驗證RFS法對辨識負剛度非線性振子的有效性和準確性。
1 多穩(wěn)態(tài)懸臂梁非線性回復力建模
為實現(xiàn)對稱和非對稱多穩(wěn)態(tài)懸臂梁結構,通常采用外部磁鐵耦合的方法[4-5],且靠近懸臂梁末端對稱布置兩塊可旋轉磁鐵。由于磁力的相互作用會改變懸臂梁的穩(wěn)態(tài)特性,當兩塊磁鐵旋轉角度不一樣時會形成圖1所示的不對稱多穩(wěn)態(tài)結構。本文采用多穩(wěn)態(tài)磁耦合懸臂梁進行研究分析。

(a)對稱雙穩(wěn)態(tài) (b)不對稱雙穩(wěn)態(tài) (c)對稱三穩(wěn)態(tài) (d)不對稱三穩(wěn)態(tài)
實踐經(jīng)驗表明,非線性回復力是磁場力和線性回復力共同作用產(chǎn)生的,則非線性回復力Fr表示為
(1)
式中:K為懸臂梁線的等效剛度;p為非線性項個數(shù);L表示0、1或-1;k為各非線性項系數(shù);u為懸臂梁末端位移。
為了探究4種典型多穩(wěn)態(tài)懸臂梁的回復力方程,需要這4種結構最簡單的回復力表征形式。當回復力方程中p=3時,便可以構造出雙穩(wěn)態(tài)懸臂梁,此時非線性回復力為
Fbi=(K+L1k1)u+L2k2u2+L3k3u3
(2)
非線性勢能函數(shù)包括兩個穩(wěn)定平衡點(勢阱)和一個不穩(wěn)定平衡點(勢壘),其中偶次項系數(shù)決定了系統(tǒng)是否不對稱,若為零則完全對稱,該函數(shù)為回復力在位移上的積分如下
(3)
當回復力方程中p=5時,非線性回復力方程為
Ftri=(K+L1k1)u+L2k2u2+L3k3u3+
L4k4u4+L5k5u5
(4)
非線性勢能函數(shù)有3個穩(wěn)定平衡點(勢阱)和兩個不穩(wěn)定平衡點(勢壘),回復力中偶數(shù)項次數(shù)決定了系統(tǒng)不對稱,表示如下
(5)
實踐中,不會先確定非線性回復力各項系數(shù)后再設計一個多穩(wěn)態(tài)結構,這也是需要辨識的內(nèi)容。但是,可以先確定穩(wěn)態(tài)點位置和不穩(wěn)定點位置,再選取合理的K+L1k1范圍設計多穩(wěn)態(tài)結構,這里定義K+L1k1為主剛度項系數(shù)。
對于雙穩(wěn)態(tài)結構,通常設不穩(wěn)定平衡點u2為零作為一個基準,其余兩項非線性系數(shù)為
L4k3=(K+L1k1)/u1u3;L2k2=-L3k3(u1+u3)
(6)
對于三穩(wěn)態(tài)結構,若將3個穩(wěn)定平衡點位置u1、u3、u5和兩個不穩(wěn)定平衡點位置u2、u4(u3通常設為0)作為基準,其余4項非線性系數(shù)可表達為
(7)
2 非參數(shù)辨識原理
2.1 RFS法辨識原理
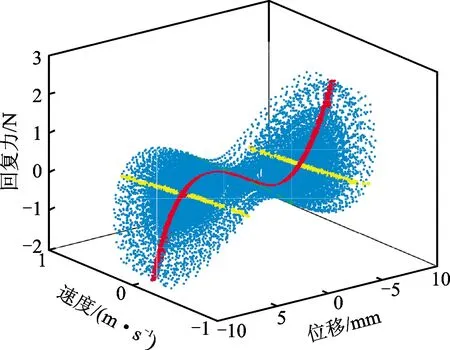
RFS法是一個僅在少量系統(tǒng)結構信息下,利用時域信號進行系統(tǒng)辨識的方法。其原理是從懸臂梁的時域響應軌跡中構造出力、速度和位移的三維數(shù)據(jù)。從力-位移截面得到剛度力曲線,從力-速度截面得到阻尼力曲線,NRF的系數(shù)可以通過最小二乘擬合得到。RFS能夠通過三維曲面直觀地看出系統(tǒng)的動力學特性,真實地表征NRF。
對于一非線性單自由度系統(tǒng),根據(jù)牛頓第二定理有
(8)

根據(jù)哈密頓原理,具有磁耦合的多穩(wěn)態(tài)懸臂梁的集中參數(shù)模型如下
(9)
式中:C為懸臂梁等效黏性阻尼。實驗中,磁力耦合非線性懸臂梁系統(tǒng)的M和激勵f(t)為已知量,加速度和速度可通過數(shù)值微分計算得到,那么將式(7)(8)進行變換,依據(jù)采樣定理,以Δt為時間間隔,采樣的ti=(i-1)Δt表示第i個采樣時間點,那么在時間點i上有
(10)
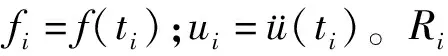
(11)
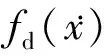
(12)
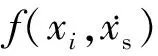
(13)
式中:c=(c0,…,cn)T。
同樣地,利用阻尼曲線可以得到回復力曲面在x=0處的剖面曲線。對這條曲線進行多項式擬合,可以得到阻尼力曲線的表達式如下
(14)
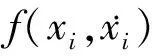
(15)
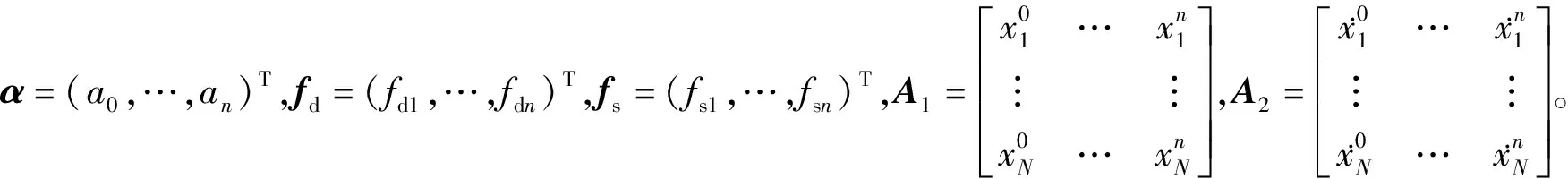
2.2 數(shù)據(jù)處理
RFS的關鍵問題是必須同時得到每個采樣點的位移、速度和加速度,然而要通過實驗同時測量這3個量又是不現(xiàn)實的,目前有多種方法來解決這個問題,其中最直接的兩種方法為時域上的數(shù)值積分和數(shù)值微分。根據(jù)采樣定理,做微分或者是積分運算要求時間域數(shù)據(jù)要足夠多,采樣的頻率要足夠高,所以采樣頻率應至少為最高頻率的10倍以上。
2.2.1 時域上的數(shù)值積分 數(shù)值積分的方法有Trapezium公式、Simpson公式、Tick公式等。Trapezium公式的具體形式如下
(16)
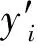
(17)
式中:A、B都為常數(shù)。
Simpson公式如下
(18)
Tick公式如下
(19)
因為在計算積分達到相同精度的情況下,Trapezium公式計算量少,計算過程簡單,計算速度更快。所以本文用Trapezium公式對一個微分方程的實例進行驗證
(20)
(a)速度
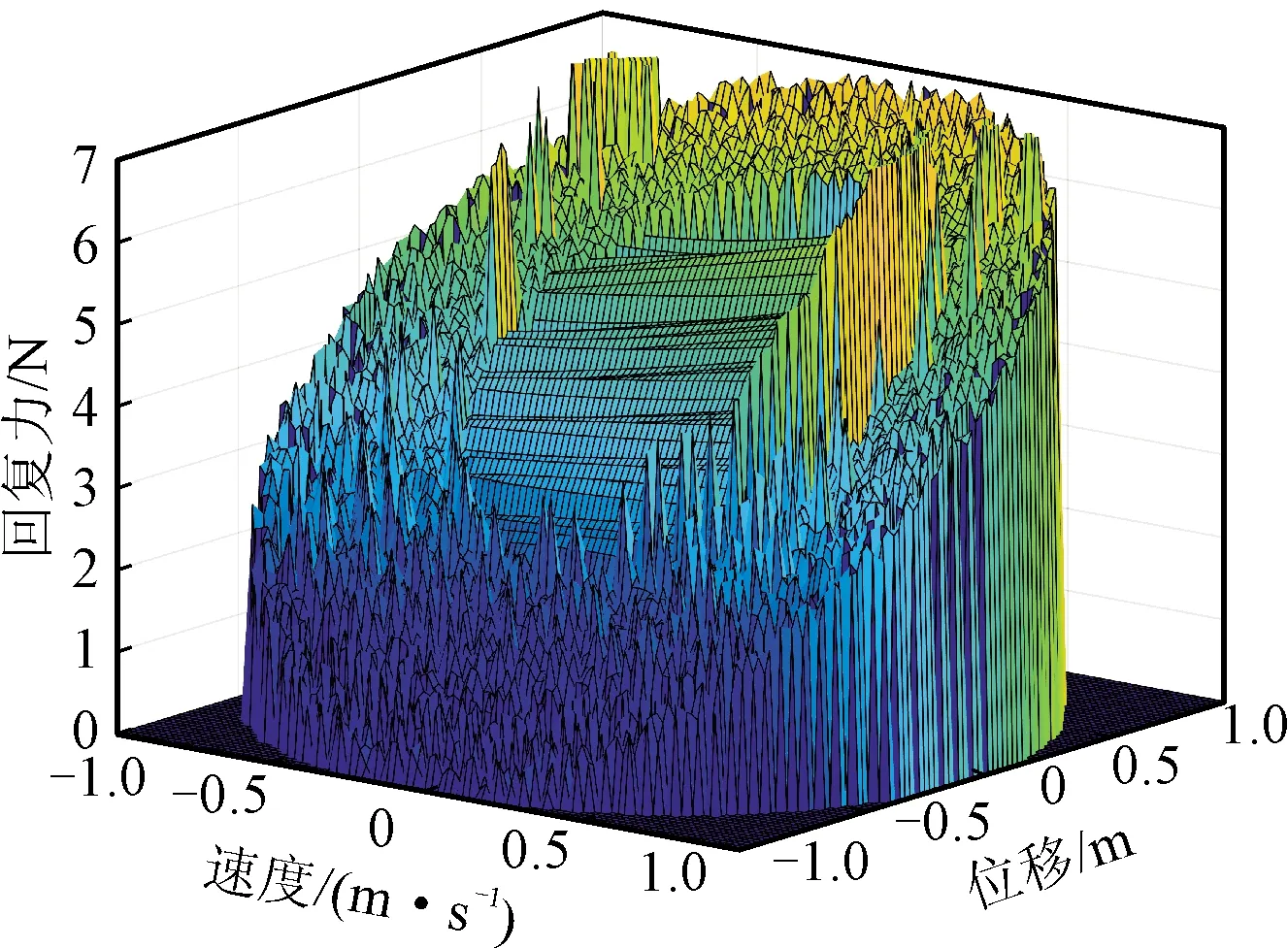
圖3 時域數(shù)值積分下得到的回復力曲面
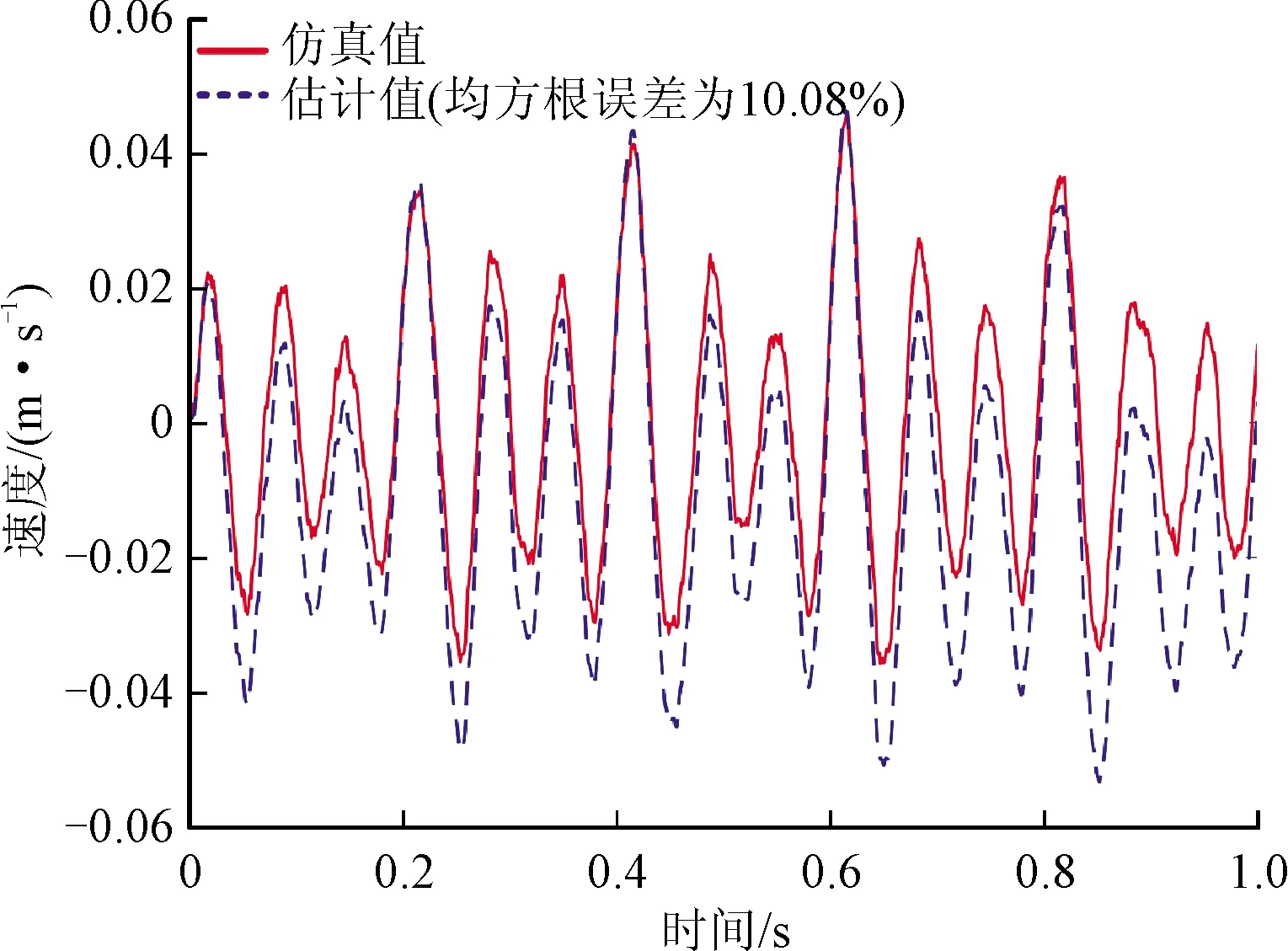
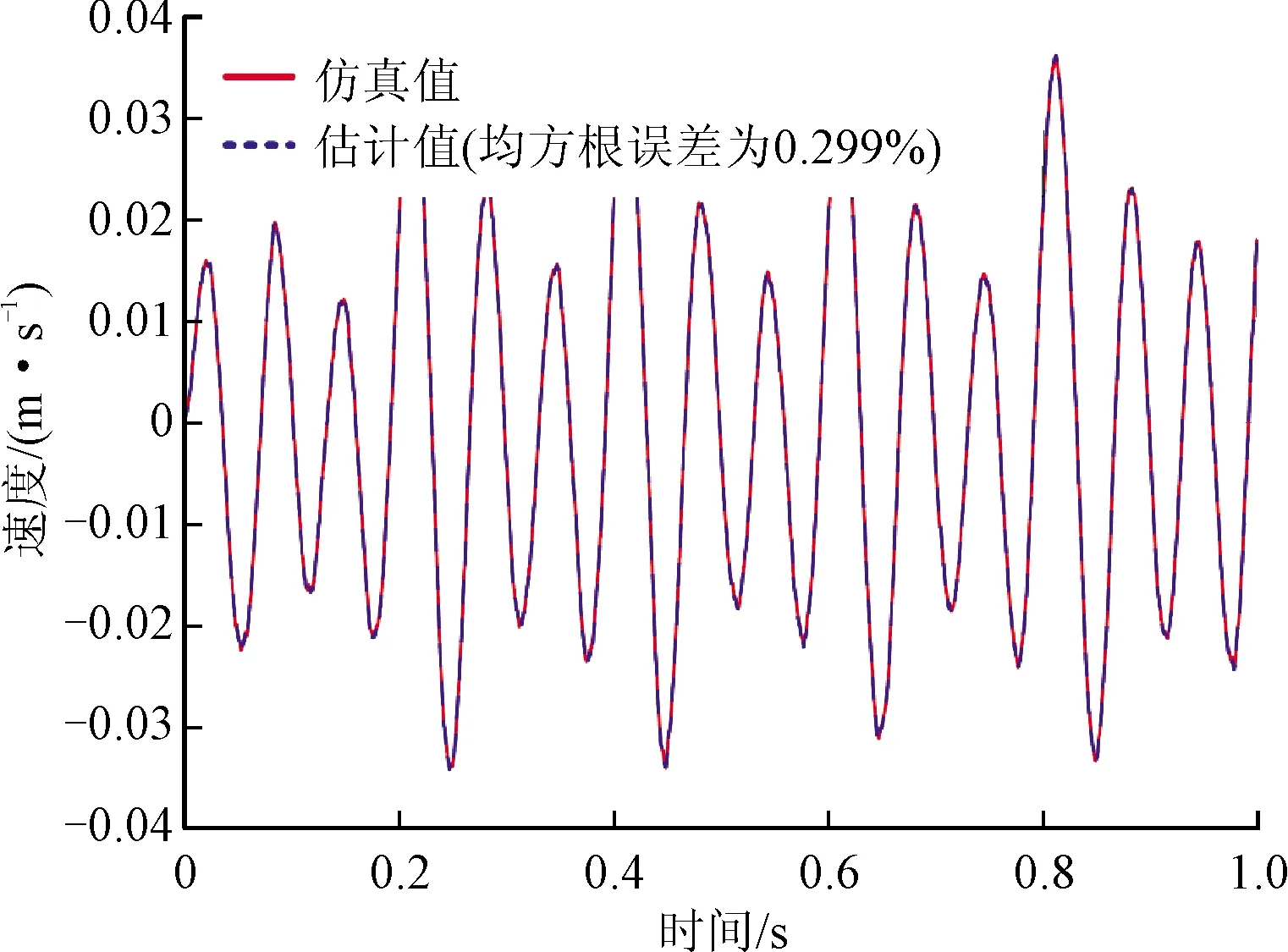
仍用上文中的例子,再次利用Trapezium公式進行兩次積分運算,得到速度和位移的真實值與估計值,如圖4所示。這時,速度真實值和估計值之間的均方根誤差為0.278 9%,而位移的真實值和估計值之間的均方根誤差為6.322 4%。從圖5可以看出系統(tǒng)是線性的,尤其是位移的真實值和積分值的比較,移除趨勢項后的估計值準確性提高了很多。
(a)速度
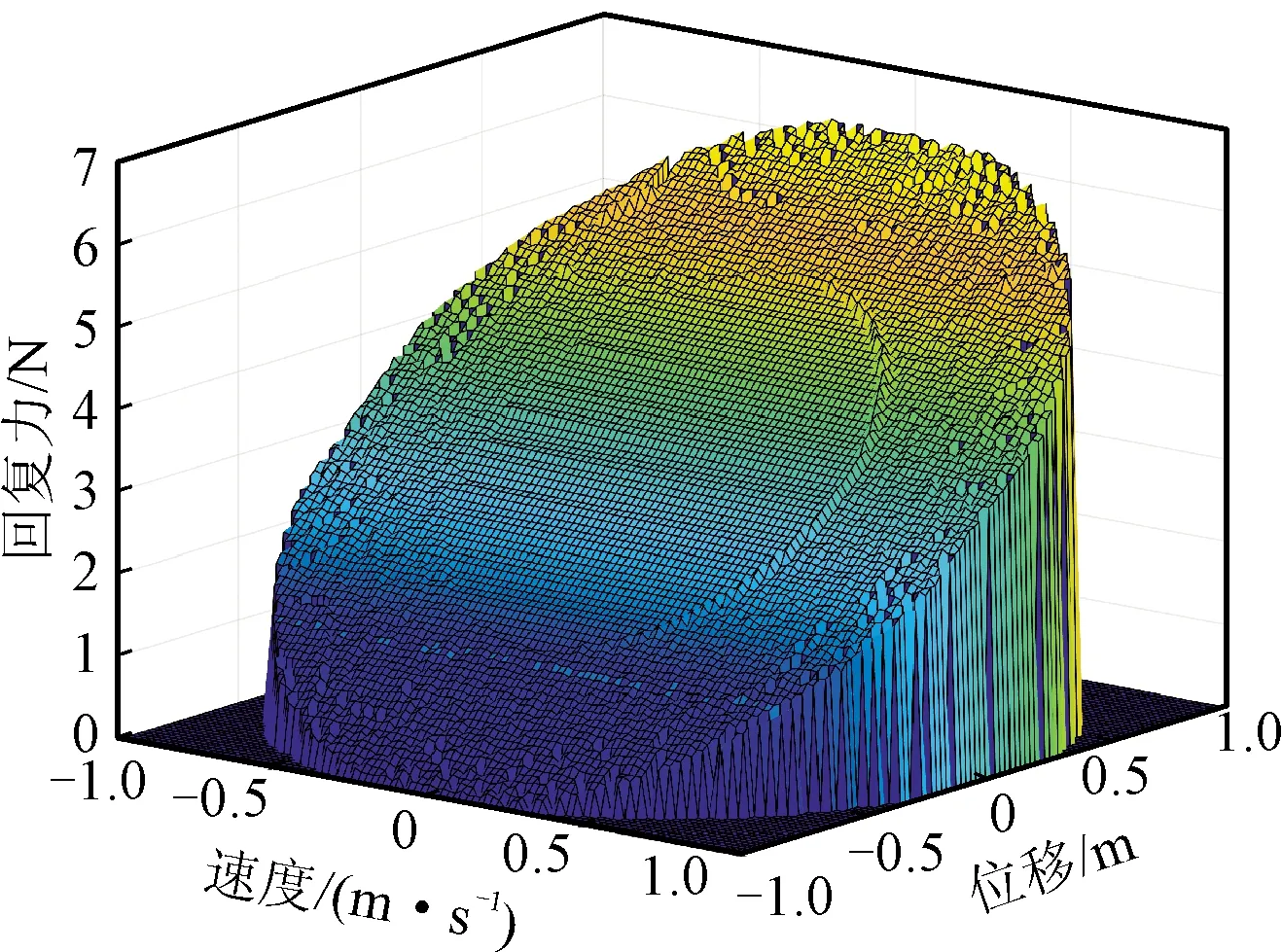
圖5 去趨勢項后時域數(shù)值積分下得到的回復力曲面
2.2.2 時域上的數(shù)值微分 實驗中,如果得到的是位移信號或者是速度信號,那么就要對其做數(shù)值微分計算。數(shù)值微分計算有多種公式,這里介紹3、5、7數(shù)值點微分公式。3數(shù)值點微分公式
(21)
5數(shù)值點微分公式
(22)
7數(shù)值點微分公式
50(yi+1-yi-1)]/60Δt
(23)
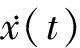
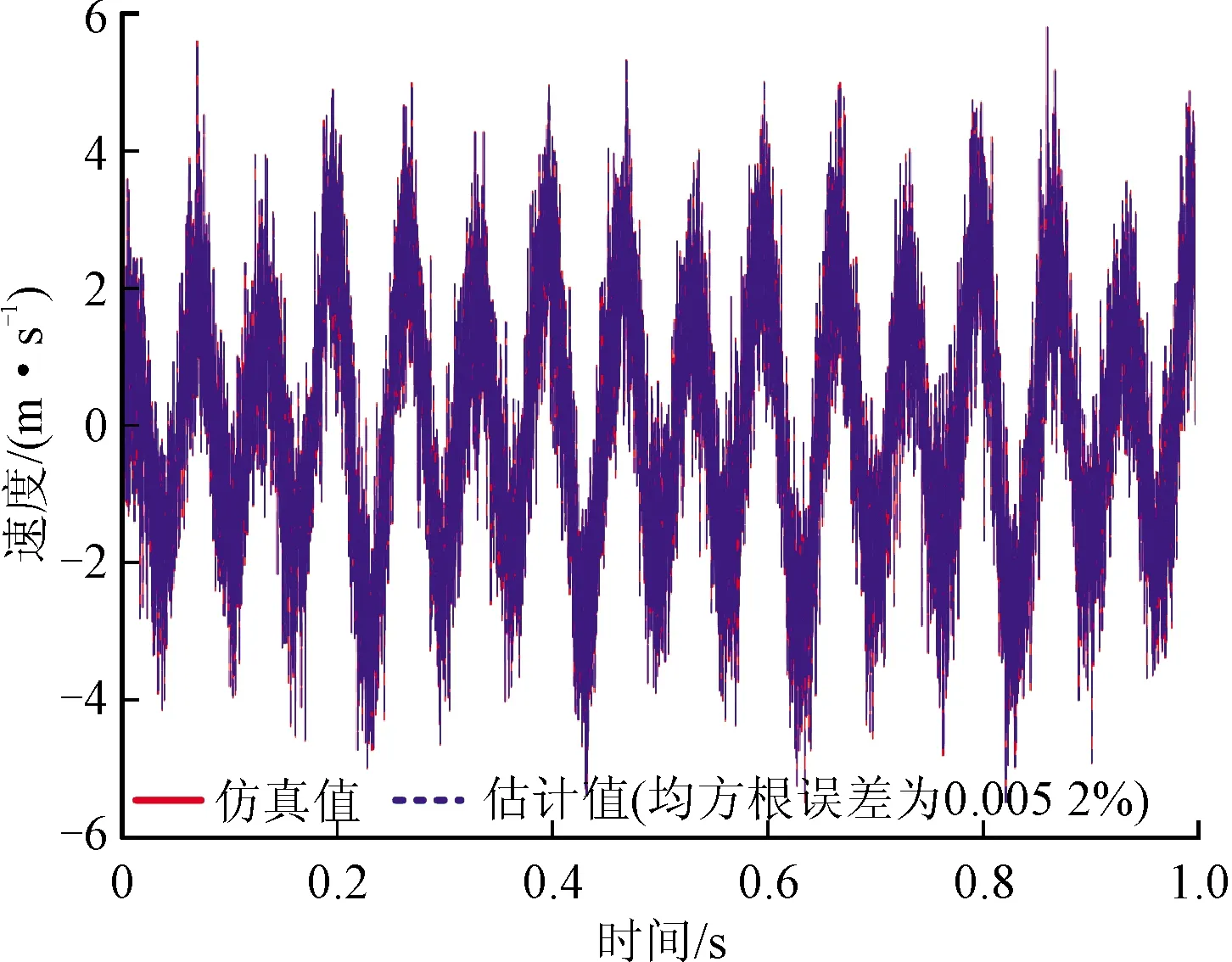
(a)速度
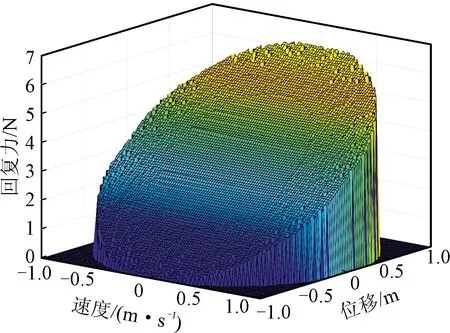
圖7 時域數(shù)值微分下得到的回復力曲面
因為時域積分對測得的加速度信號直接進行積分會出現(xiàn)干擾趨勢項,需要擬合趨勢項以去除信號偏移,并且因為安裝要求無法準確測量懸臂梁的加速度,所以通過測量位移信號,采用7數(shù)值點微分公式進行數(shù)值微分,完成回復力曲面的繪制。因為本節(jié)通過一個線性微分方程對傳統(tǒng)的回復力曲面法進行驗證,對回復力曲面做了處理,將速度和位移線性映射到[-1,1]區(qū)域,能更加直觀對比。對于多穩(wěn)態(tài)系統(tǒng),將曲面投影至xoy坐標無法直觀地看出系統(tǒng)的非線性特性,所以將直接在三維空間表征RFS。
3 仿真分析
根據(jù)第2節(jié)原理,構造出4種不同類型的負剛度懸臂梁。對4種類型多穩(wěn)態(tài)振子進行仿真研究,分析剛度回復力和阻尼回復力的辨識精度。表1列出了4種不同類型的振子的參數(shù)。
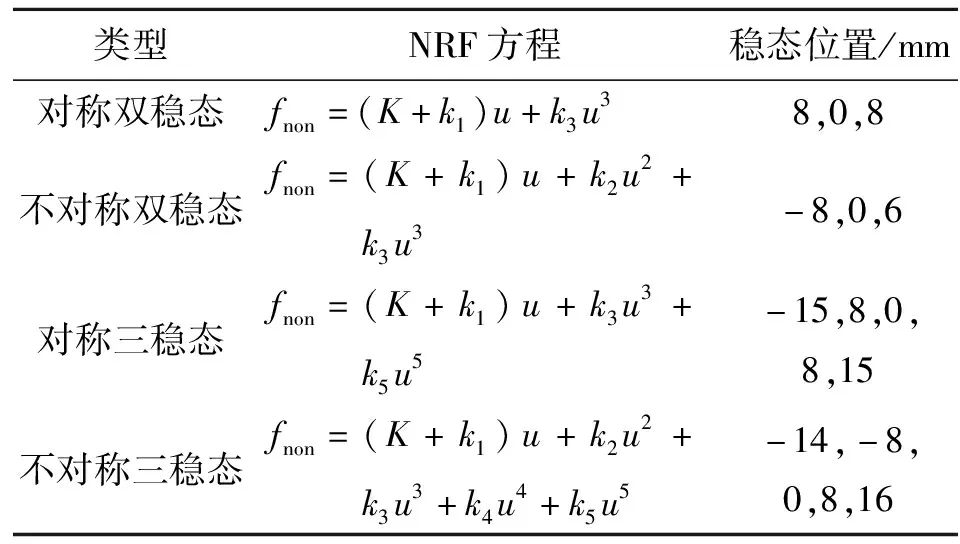
表1 4種不同類型負剛度懸臂梁的參數(shù)
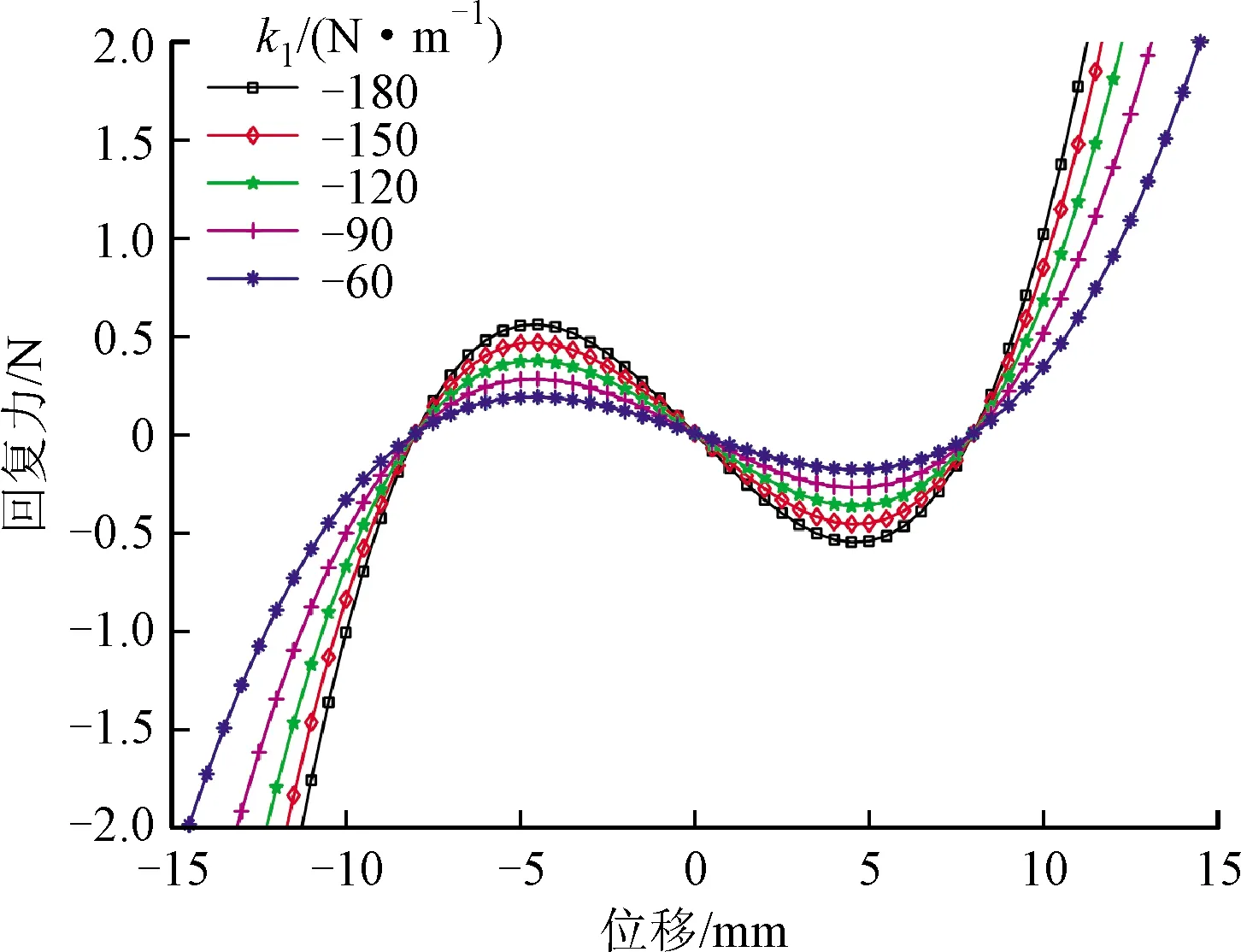
根據(jù)上文需給出梁的等效剛度K和非線性磁力的一階多項式系數(shù)。選取K為112 N/m,非線性剛度系數(shù)k1為-180~-60 N/m,如圖8所示,k1可以確定雙穩(wěn)態(tài)或三穩(wěn)態(tài)振子的勢阱深度。仿真中,考慮了對稱雙穩(wěn)態(tài)和非對稱雙穩(wěn)態(tài)懸臂梁的k1=-120 N/m,對稱三穩(wěn)態(tài)和不對稱三穩(wěn)態(tài)懸臂梁的k1=-100 N/m,懸臂梁的等效質(zhì)量M和黏滯阻尼C分別為0.006 kg和0.01 N·s/m。
(a)對稱雙穩(wěn)態(tài)
表2為依據(jù)穩(wěn)態(tài)點和主剛度項系數(shù)構造的4種類型的NRF方程。

表2 4種類型的NRF方程
值得注意的是,雙穩(wěn)態(tài)和三穩(wěn)態(tài)懸臂梁可以表現(xiàn)為勢阱間振蕩或勢阱內(nèi)振蕩,識別數(shù)據(jù)集的選擇尤為重要。數(shù)值算例表明,選擇的輸出位移信號必須同時包含勢阱間振蕩和勢阱內(nèi)振蕩。本文選取恒激勵加速度的掃頻信號,保證輸入激勵力幅值恒定。得到懸臂梁的位移,通過微分得到速度和加速度,構造出力、速度、位移的三維點,用Grawley-O’Donnel法將這些點通過插值,繪制成象限上的連續(xù)曲面得到RFS,如圖9所示。從RFS圖中能夠直觀的觀測系統(tǒng)的非線性特性及穩(wěn)態(tài)點位置,說明數(shù)值微分方法能夠可靠地從測量位移中估計到速度和加速度的值,從而完成系統(tǒng)RFS的精準繪制。通過截面法得到,系統(tǒng)剛度回復力曲線和阻尼回復力曲線見圖10。從剛度回復力曲線可以看出系統(tǒng)的負剛度穩(wěn)態(tài)特性及其穩(wěn)態(tài)點位置,從阻尼曲線可看出系統(tǒng)的阻尼是線性的。用最小二乘法對回復力參數(shù)進行辨識,結果見表3,RFS辨識得到的剛度回復力曲線的辨識精度大于95%,辨識得到的阻尼回復力曲線的誤差不超過5%,辨識結果和仿真值吻合度高,說明回復力曲面法對磁力耦合多穩(wěn)態(tài)非線性懸臂梁系統(tǒng)辨識的精確性和有效性。
(a)對稱雙穩(wěn)態(tài)
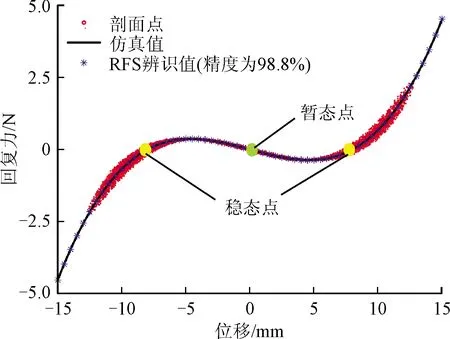
(a)對稱雙穩(wěn)態(tài)剛度力曲線

表3 4種典型負剛度非線性振子回復力參數(shù)辨識結果
4 實驗驗證
為驗證計算方法和非線性回復力辨識精度,搭建了如圖11所示的實驗系統(tǒng)。系統(tǒng)是由信號發(fā)生器(VT-9002-1)和功率放大器(YE5874A)控制的激振器(JZK-50)在恒定頻率和掃頻激勵下建立的。用位移傳感器(HL-G112-A-C5)測量懸臂梁響應的絕對位移,用示波器(TBS2000)采集實驗數(shù)據(jù)。由于懸臂梁的內(nèi)部應力、兩個旋轉磁鐵的不均勻性以及安裝條件等原因,很難實現(xiàn)完全對稱,因此如果懸臂梁兩個穩(wěn)態(tài)點的位置相對于中心位置的誤差小于5%,則視為對稱。
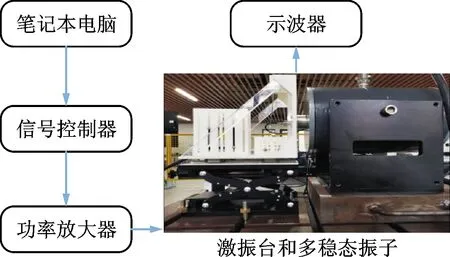
圖11 實驗系統(tǒng)組成
4種不同類型的多穩(wěn)態(tài)振子的穩(wěn)態(tài)點位置如表4所示,它們是通過旋轉磁體或改變磁體的相對位移來實現(xiàn)的,此外其他實驗參數(shù)也列于表4。
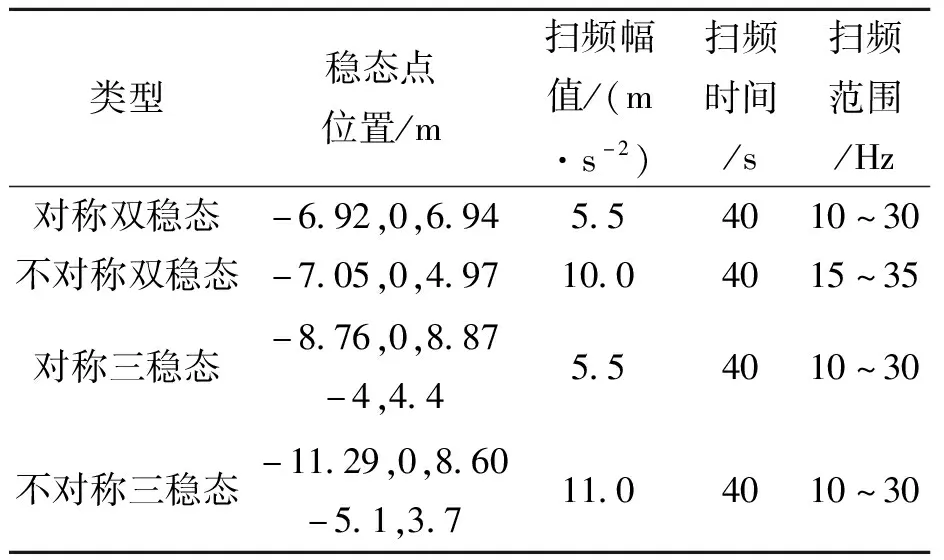
表4 4種不同類型的多穩(wěn)態(tài)懸臂梁的實驗參數(shù)
根據(jù)第2節(jié),RFS方法可用于系統(tǒng)回復力的辨識,包括剛度回復力和阻尼回復力。因此,對多穩(wěn)態(tài)梁的位移響應進行了測量和處理,包括對采集位移信號的平滑處理和數(shù)值微分,以構建RFS。圖12顯示了對稱雙穩(wěn)態(tài)懸臂梁系統(tǒng)的實驗結果,不對稱雙穩(wěn)態(tài)系統(tǒng)、對稱三穩(wěn)態(tài)系統(tǒng)及不對稱三穩(wěn)態(tài)系統(tǒng)實驗結果如圖13~15所示。從中可以看出,回復力曲面法能直觀地展示實驗數(shù)據(jù)的非線性特性,其中剛度回復力的擬合精度為97%以上,阻尼回復力的擬合精度為94%以上,所以通過剛度和阻尼函數(shù)的精確辨識,能夠更加準確地顯示系統(tǒng)的非線性特性。通過大量的仿真數(shù)據(jù)和實驗數(shù)據(jù)集辨識結果可知,RFS的辨識精度很大程度上取決于數(shù)據(jù)的前處理。總之,辨識出的NRF與測量的RFS有很好的一致性,驗證了RFS法對辨識負剛度非線性振子的有效性和準確性。
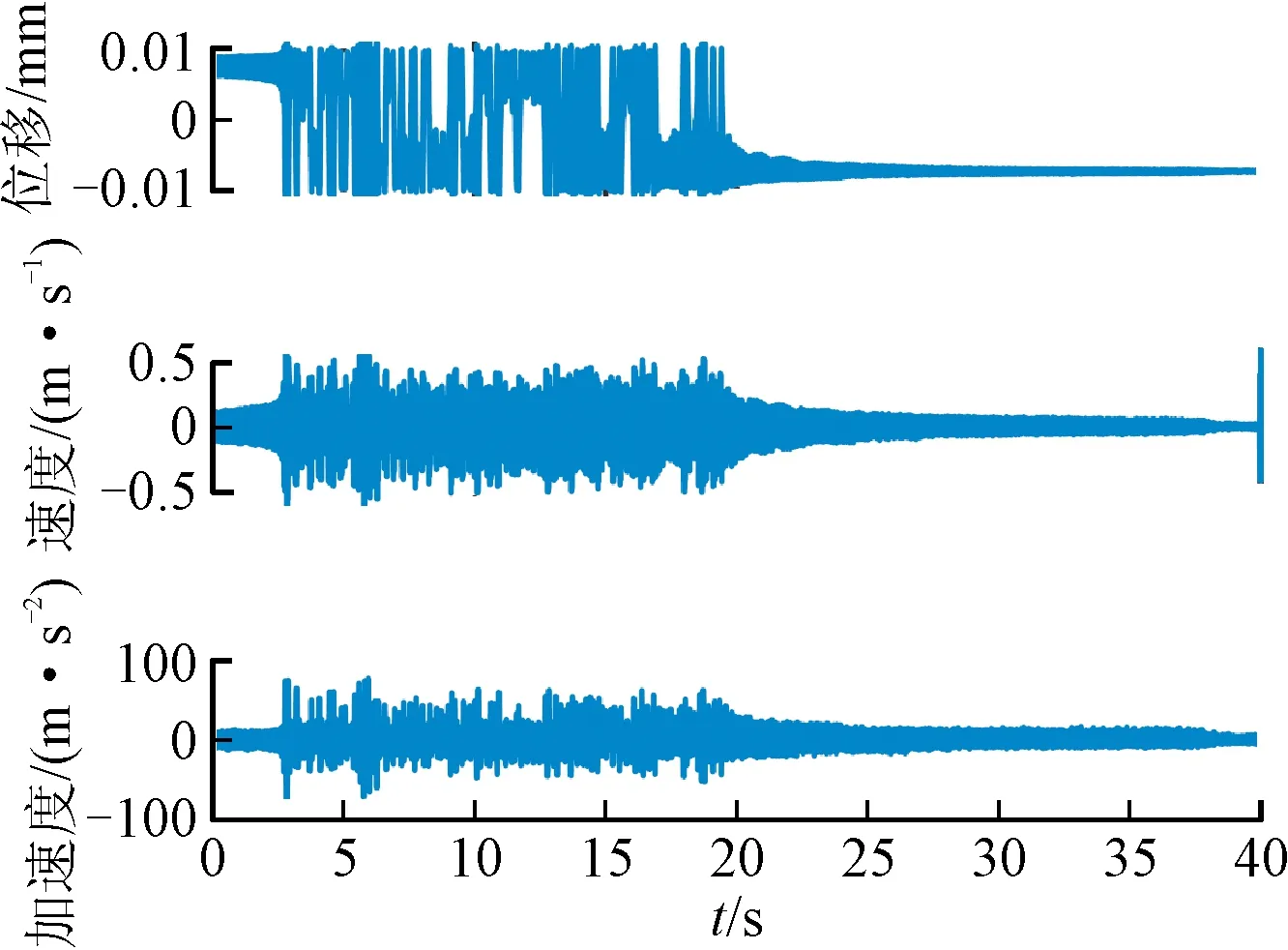
(a)測量位移數(shù)值微分結果
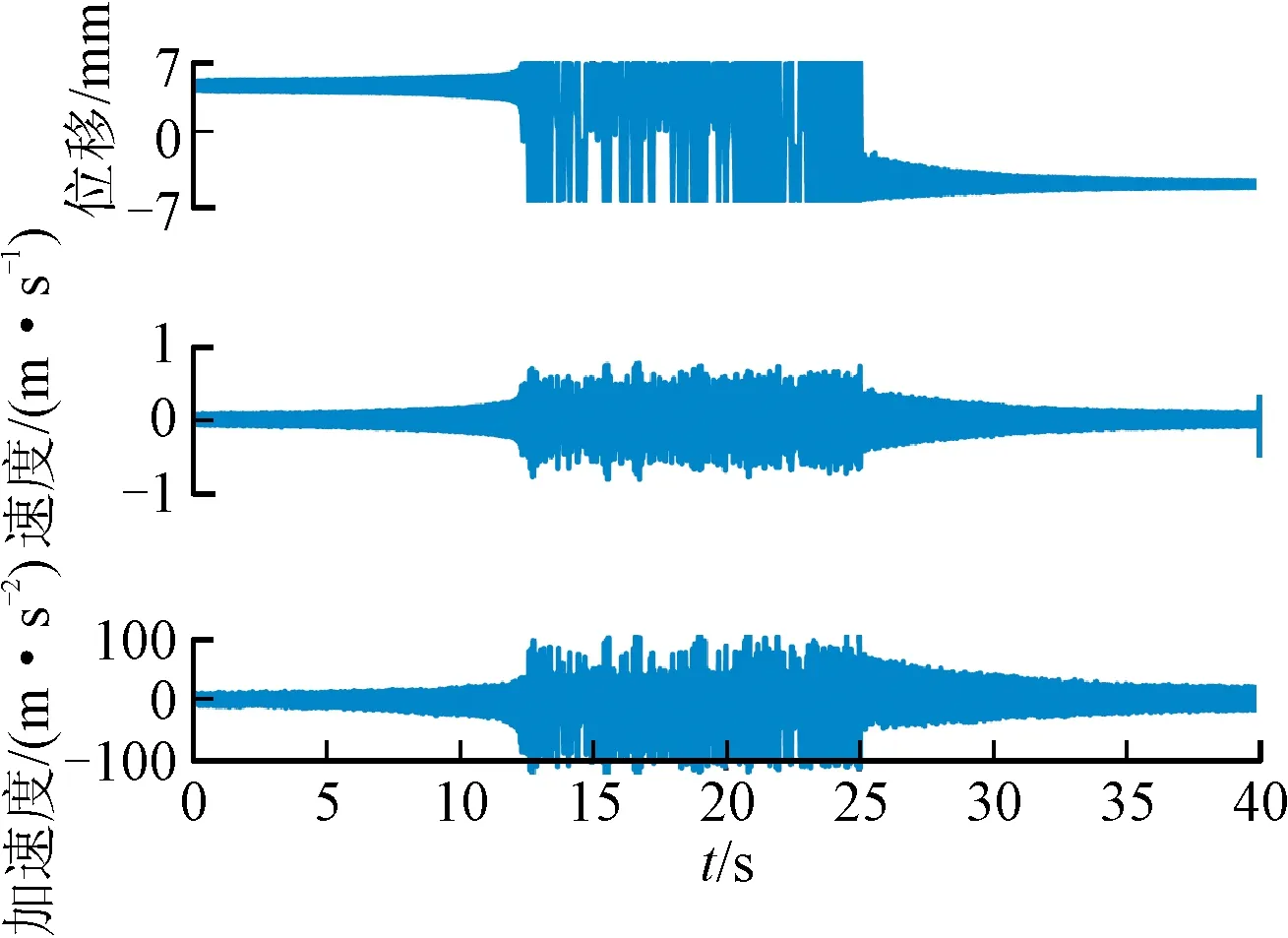
(a)測量位移數(shù)值微分結果
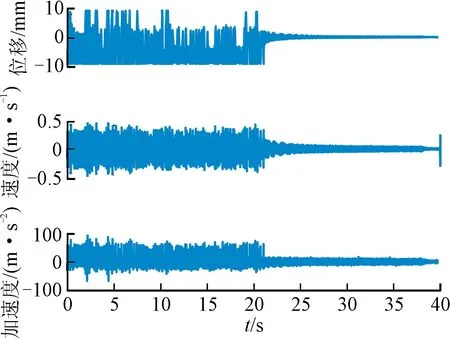
(a)測量位移數(shù)值微分結果
5 結 論
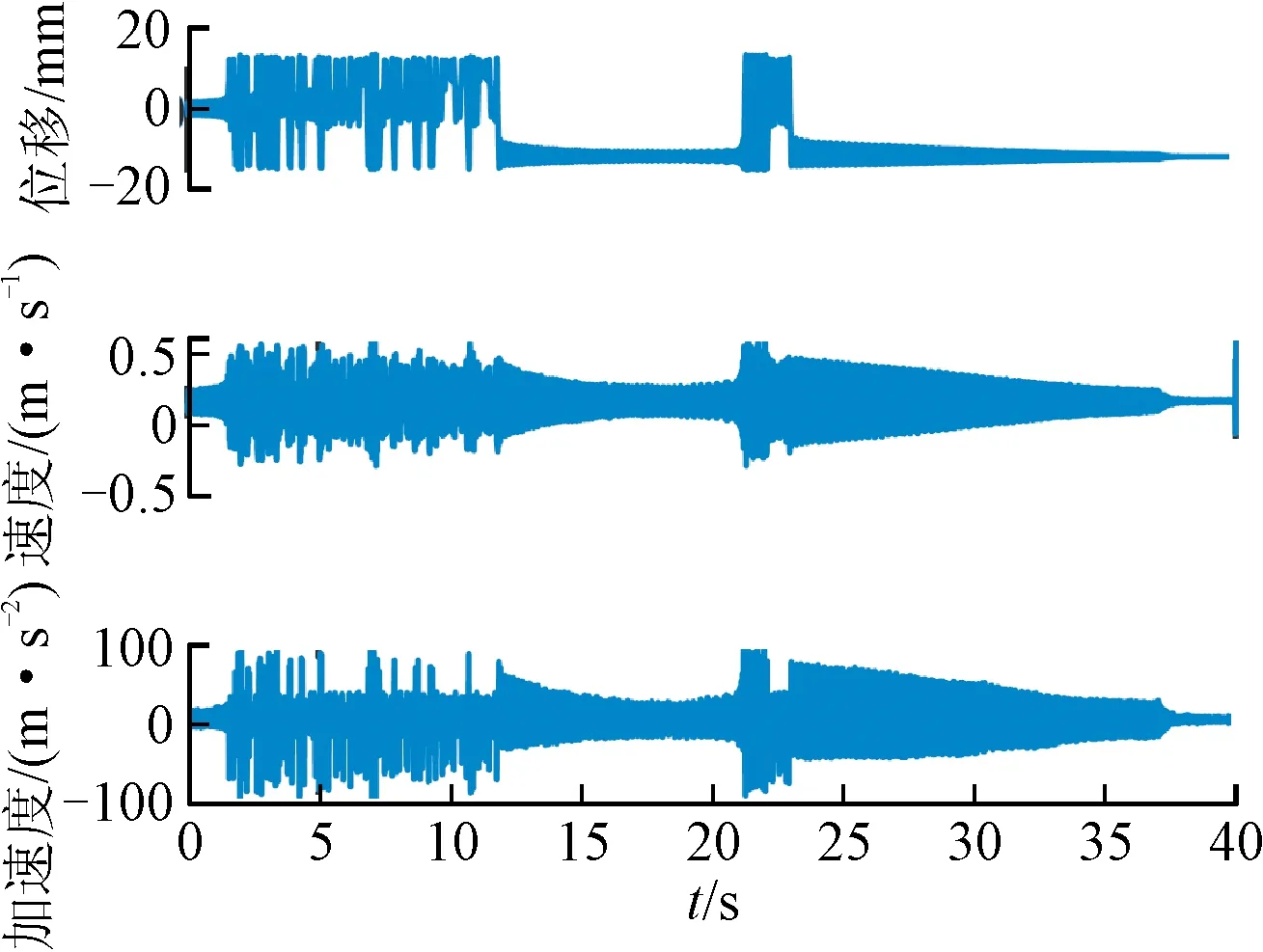
(a)測量位移數(shù)值微分結果
(1)對比分析了位移微分和加速度積分的數(shù)值處理方法,數(shù)值模擬結果表明,對時域數(shù)值積分進行趨勢項去除后的精度能達到93%以上,對時域數(shù)值微分的精度能達到99%以上。所以,微分處理辦法比積分處理辦法更好,對位移數(shù)據(jù)的微分處理精度可達99%。
(2)基于RFS法的非參數(shù)辨識方法,辨識得磁耦合多穩(wěn)態(tài)懸臂梁系統(tǒng),數(shù)值模擬結果表明,通過對數(shù)據(jù)集中加入40、20和10 dB的高斯白噪聲,在不同勢阱下,剛度回復力和阻尼回復力的辨識精度都能保證95%以上。
(3)實驗結果表明,識別結果與實測回復力面吻合很好,依據(jù)最小二乘法,在不同勢阱下的剛度回復力擬合精度能保證在97%以上,阻尼回復力辨識精度能保證在94%以上,證明了回復力曲面法對辨識負剛度非線性振子的有效性和準確性。
(4)通過RFS法對實測數(shù)據(jù)進行繪制得到的三維回復力曲面,能夠直觀地看到系統(tǒng)的非線性特性及穩(wěn)態(tài)位置。本文是RFS法在負剛度及多穩(wěn)態(tài)非線性系統(tǒng)中的首次應用。
(5)負剛度結構的發(fā)展提高了能量俘獲或振動控制能力,回復力曲面法可以將非線性回復力精準的表征出來,此研究結果為能量俘獲及振動控制領域的非線性研究提供了一種可行的方法。

