基于多目標(biāo)優(yōu)化的燃料電池汽車實時能量管理策略

于坤杰, 王思雨, 楊 朵, 符漢文, 廖粵峰

(鄭州大學(xué) 電氣與信息工程學(xué)院,河南 鄭州 450001)

為了實現(xiàn)“碳達(dá)峰”和“碳中和”戰(zhàn)略目標(biāo),構(gòu)建新能源占比逐步提高的能源系統(tǒng)成為未來重大發(fā)展方向。在交通領(lǐng)域,燃料電池汽車代替?zhèn)鹘y(tǒng)內(nèi)燃機汽車成為實現(xiàn)這一戰(zhàn)略目標(biāo)的有效途徑[1]。

然而,燃料電池在汽車行業(yè)的應(yīng)用也存在一些問題。燃料電池的動態(tài)響應(yīng)比較緩慢,且無法回收車輛制動產(chǎn)生的能量,因此,將燃料電池和其他儲能元件混合使用成為更好的選擇[2]。常見的混合能源有“燃料電池+鋰電池”、“燃料電池+超級電容+鋰電池”以及“鋰電池+超級電容”[3]。混合動力系統(tǒng)的關(guān)鍵問題在于如何分配不同能源之間的能量。目前,國內(nèi)外諸多科研機構(gòu)與研究團(tuán)隊對燃料電池的能量管理策略(energy management strategy, EMS)進(jìn)行了深入的研究,其內(nèi)容大致分為兩類,一類是基于規(guī)則的EMS,另一類是基于優(yōu)化的EMS。基于規(guī)則的EMS能夠根據(jù)專家經(jīng)驗和操作知識,設(shè)計功率分配規(guī)則,使得燃料電池盡可能在高效率區(qū)間運行,主要包括模糊邏輯[4-5]、小波變換[6]、有限狀態(tài)機[7]等,但在未知道路環(huán)境缺乏適應(yīng)性。基于優(yōu)化的EMS將氫耗和電池耐久性等多項指標(biāo)作為目標(biāo)函數(shù),通過優(yōu)化算法對目標(biāo)進(jìn)行優(yōu)化,進(jìn)而達(dá)到較優(yōu)的功率分配性能,可分為全局優(yōu)化和瞬時優(yōu)化。全局優(yōu)化方法主要包括動態(tài)規(guī)劃法(DP)[8-9]、遺傳算法[10-11]、粒子群優(yōu)化[12]等一些其他的元啟發(fā)式算法。例如,Hassan等[13]提出了改進(jìn)的白鯨算法,將其應(yīng)用于大規(guī)模電力系統(tǒng)的經(jīng)濟(jì)負(fù)荷調(diào)度問題。Pan等[14]提出了基于模糊邏輯和灰狼算法的EMS,通過分析駕駛行為和環(huán)境因素來預(yù)測未來的駕駛情況。然而,基于全局優(yōu)化的EMS存在計算量大、難以實際應(yīng)用等問題。瞬時優(yōu)化方法能夠在采樣周期內(nèi)進(jìn)行實時尋優(yōu),相比于全局優(yōu)化方法具有計算量較小、實時性更高等優(yōu)點。Zhang等[15]提出了一種基于等效氫耗量最小原則的功率分配策略,能夠有效優(yōu)化駕駛性能,提高經(jīng)濟(jì)性。Shen等[16]和Nie等[17]采用模型預(yù)測控制方法進(jìn)行混合動力系統(tǒng)的能量調(diào)度,驗證了算法的經(jīng)濟(jì)性能。混合動力系統(tǒng)的性能受制于復(fù)雜隨機的環(huán)境工況,因此,實時功率分配策略的設(shè)計難點在于如何針對不同的負(fù)載場景,提升算法的自適應(yīng)能力,并實時、快速地給出最佳分配規(guī)則。

為了解決上述問題,本文將規(guī)則策略與優(yōu)化算法相結(jié)合,提出了一種混合型的優(yōu)化策略來解決多目標(biāo)多約束下的能量管理問題。本文的主要研究貢獻(xiàn)如下。

(1)根據(jù)燃料電池的效率特性,提出了一種基于規(guī)則的多模式能量管理策略,該策略能夠使燃料電池長時間運行在高效率區(qū)。

(2)為了降低系統(tǒng)的氫耗量并且延長燃料電池使用壽命,基于多目標(biāo)白鯨優(yōu)化算法(MOBWO),對規(guī)則策略的控制參數(shù)進(jìn)行優(yōu)化。多目標(biāo)白鯨優(yōu)化算法是一種新型的基于群體的元啟發(fā)式算法,相較于其他常用的多目標(biāo)優(yōu)化算法[18-19],在開發(fā)性能、探索能力及避免局部最優(yōu)方面更加優(yōu)異[20]。

(3)提出了一種數(shù)據(jù)驅(qū)動的道路工況分類方法。利用典型路況數(shù)據(jù)集和長短期記憶網(wǎng)絡(luò)(LSTM)對駕駛路況進(jìn)行分類。

(4)對測試路況進(jìn)行實時分類,根據(jù)路況種類進(jìn)行實時功率分配,并通過實驗對比驗證了所提方法的優(yōu)越性。

1 系統(tǒng)結(jié)構(gòu)和建模

1.1 系統(tǒng)拓?fù)浣Y(jié)構(gòu)

本文采用的是最常見的半主動式的混合能源拓?fù)浣Y(jié)構(gòu),如圖1所示[21]。鋰電池直接與母線相連,減少中間能量的損失。此類結(jié)構(gòu)使鋰電池電壓與母線電壓保持一致,又能通過單向DC/DC變換器控制燃料電池的輸出電流。

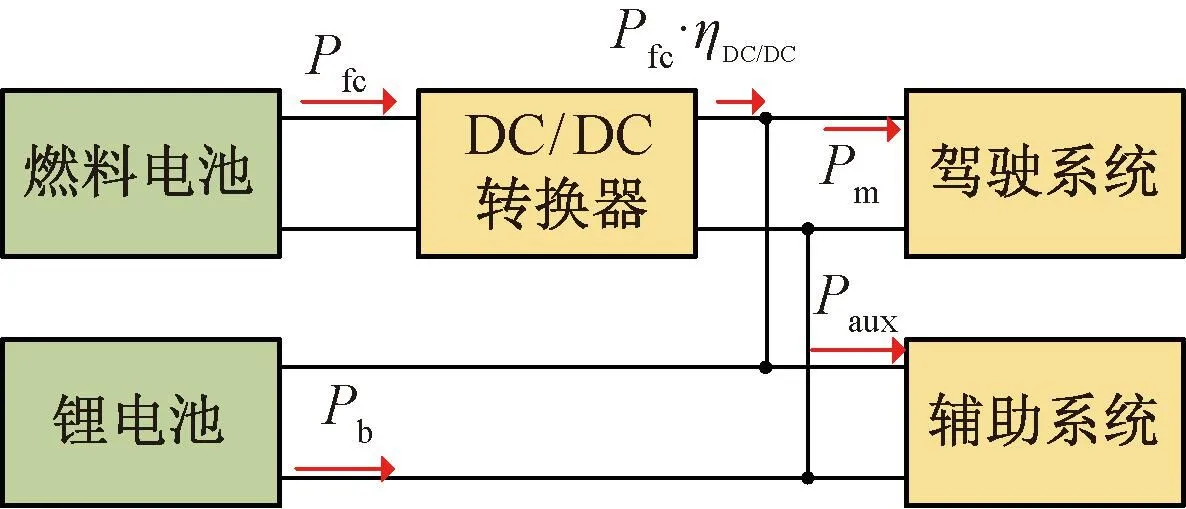
圖1 半主動式拓?fù)浣Y(jié)構(gòu)

1.2 車輛動力學(xué)模型

基于車輛的縱向動力學(xué)模型,車輛牽引力Ft通過式(1)計算:

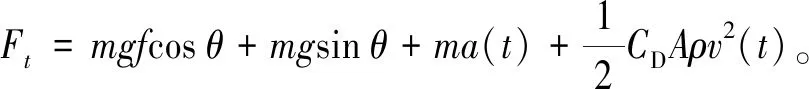
(1)

式中:m為車輛質(zhì)量,kg;f為車輛與地面的滑動摩擦力系數(shù);a(t)為行駛時的加速度,m/s2;v為車輛速度,m/s;θ為道路坡度;CD為迎風(fēng)阻力系數(shù);A為迎風(fēng)面面積,m2。模型參數(shù)及取值如表1所示[22]。

表1 車輛模型參數(shù)

總線上的負(fù)載功率與牽引力和車輛速度相關(guān):

Pm=ηFt·v。

(2)

式中:η為車輛傳動系統(tǒng)的效率。總線負(fù)載需求、燃料電池功率及鋰電池功率關(guān)系如下所示:

Pm=Pfc·ηDC/DC+Pb。

(3)

式中:Pfc為燃料電池輸出功率,W;ηDC/DC為DC/DC轉(zhuǎn)換器效率,取0.95;Pb為鋰電池輸出功率,W。

1.3 燃料電池模型

本文采用的是由330個質(zhì)子交換膜燃料電池單體串聯(lián)而成的燃料電池系統(tǒng),最大輸出功率為50 kW。由于燃料電池在整個運行系統(tǒng)中提供穩(wěn)定的輸出功率,進(jìn)而忽略燃料電池的動態(tài)響應(yīng),只考慮用靜態(tài)模型來描述燃料電池特性。其電堆功率與系統(tǒng)的輸出功率有如下關(guān)系:

Pfc=Pst-Paux。

(4)

式中:Pfc為燃料電池系統(tǒng)的凈功率,W;Pst為燃料電池電堆產(chǎn)生的功率,W;Paux為輔助系統(tǒng)消耗的總功率,包括空氣壓縮機、水泵等,W。

燃料電池的氫氣消耗量與電流成正比。如式(5)所示:

(5)

式中:N為燃料電池的數(shù)量;MH2為氫氣的摩爾質(zhì)量,g/mol;n為反應(yīng)時轉(zhuǎn)移的電子數(shù)量;F為法拉第常數(shù)。

此外,凈輸出功率與氫氣產(chǎn)生的總功率的比值可以用來定義燃料電池系統(tǒng)的輸出效率:

(6)

式中:LHV表示氫氣的低熱值。燃料電池的效率和凈功率關(guān)系如圖2所示。

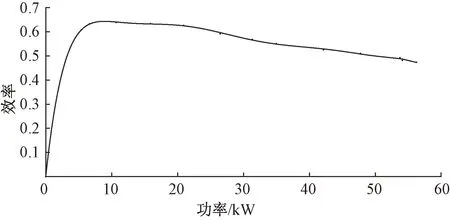
圖2 燃料電池功率-效率圖

燃料電池在使用過程中會逐步老化,根本原因是電池內(nèi)部的溫度、濕度和壓力的變化,進(jìn)而導(dǎo)致催化劑失活、膜老化、電解質(zhì)受污染和材料腐蝕等。對于混合動力汽車來說,車輛的啟停、負(fù)載變化、怠速及加速都會造成燃料電池不同程度的老化。本文采用Yue等[23]提出的燃料電池老化數(shù)學(xué)模型衡量其老化程度,如式(7)所示:

(7)

式中:p為最大允許衰減比例;kp為修正系數(shù);p1、p2、p3、p4分別為啟停、加速、怠速、負(fù)載變化的衰退速率;n1、n2、t3、t4分別表示啟停次數(shù)、加速次數(shù)、怠速時間、負(fù)載變化時間。各個參數(shù)的值如表2所示。

表2 衰退率參數(shù)

1.4 鋰電池模型

本文采用的是由100節(jié)磷酸鐵鋰動力電池串聯(lián)而成的電池組,端電壓在330 V左右。所采用的模型是高精度的R-int等效電路模型,如圖3(a)所示。其中,鋰電池電流為

(8)

圖3 鋰電池模型

式中:UOCV為鋰電池開路電壓,V;Rb為鋰電池內(nèi)阻,Ω;Pb為燃料電池的輸出功率,W。鋰電池的另一個重要指標(biāo)為鋰電池的荷電狀態(tài)SOC,如式(9)所示:

(9)

式中:Q為鋰電池容量,Ah,本研究中使用的電池容量為10 Ah。鋰電池的SOC和UOCV的關(guān)系如圖3(b)所示。

1.5 等效氫耗模型

本文考慮到燃料電池汽車在行駛途中會向鋰電池輸送能量,如果僅計算燃料電池的氫耗量而不考慮鋰電池在駕駛工況前后SOC的差值,整個混合系統(tǒng)的消耗成本會有誤差。系統(tǒng)的等效氫耗量模型如式(10)和(11)所示:

(10)

mH2=mfc+mb。

(11)

式中:mb為鋰電池的等效氫耗;mH2為整個系統(tǒng)在運行時間內(nèi)的等效氫耗量,g;nb為鋰電池個數(shù);ηfc,avg為燃料電池在工作區(qū)間內(nèi)的平均效率。

2 能量管理策略

2.1 基于規(guī)則的功率分配

本文根據(jù)車輛在駕駛過程中存在的幾種工作模式,設(shè)計了一種基于規(guī)則的功率分配策略。

(1) 啟動模式。需求功率未達(dá)到燃料電池的最小功率,且鋰電池SOC未達(dá)到設(shè)定上限時,燃料電池以最小功率運行,鋰電池吸收多余能量;當(dāng)SOC達(dá)到設(shè)定上限,多余的能量由車輛的制動電阻消耗。

(2) 節(jié)能模式。需求功率未達(dá)到燃料電池的效率最高點且鋰電池SOC未達(dá)到設(shè)定上限時,燃料電池工作在最高效率點,多余的能量由鋰電池吸收;當(dāng)鋰電池的SOC達(dá)到設(shè)定上限后,燃料電池以最小功率運行,鋰電池補充剩余功率。

(3) 低功率模式。設(shè)定燃料電池工作點1。當(dāng)車輛需求功率未達(dá)到工作點1,且鋰電池SOC未達(dá)到設(shè)定下限時,燃料電池工作在工作點1,鋰電池吸收多余能量;當(dāng)SOC隨著充電達(dá)到設(shè)定下限時,燃料電池以最高效率點時的功率與工作點1之和的k倍運行;當(dāng)SOC隨著充電達(dá)到設(shè)定值SOC1時,燃料電池工作在最高效率點;當(dāng)鋰電池的SOC隨著充電達(dá)到設(shè)定上限時,燃料電池以最小功率運行,不足的能量由鋰電池補足。

(4) 中低功率模式。設(shè)定燃料電池工作點2,SOC設(shè)定值SOC2。車輛需求功率未達(dá)到工作點2且SOC未達(dá)到設(shè)定下限時,燃料電池工作在工作點2,工作規(guī)則與低功率模式相同。

(5) 中高功率模式。設(shè)定燃料電池在此模式下工作點為最大功率點,SOC設(shè)定值SOC3。車輛需求功率未達(dá)到燃料電池最大功率且SOC未達(dá)到設(shè)定下限時,燃料電池以最大功率運行,工作規(guī)則與低功率模式相同。

(6) 高功率模式。車輛需求功率達(dá)到燃料電池的最大功率,鋰電池SOC達(dá)到設(shè)定下限時,燃料電池以最大功率運行,鋰電池不提供能量,此時提供的能量不足以滿足需求功率;當(dāng)SOC未達(dá)到設(shè)定下限時,燃料電池以功率點2與最大功率之和的k倍運行,不足的能量由鋰電池提供;當(dāng)SOC達(dá)到設(shè)定上限時,燃料電池以最小功率運行。

工作流程如圖4所示。根據(jù)圖4計算出燃料電池的輸出功率,進(jìn)而通過式(3)推出鋰電池所需輸出功率。

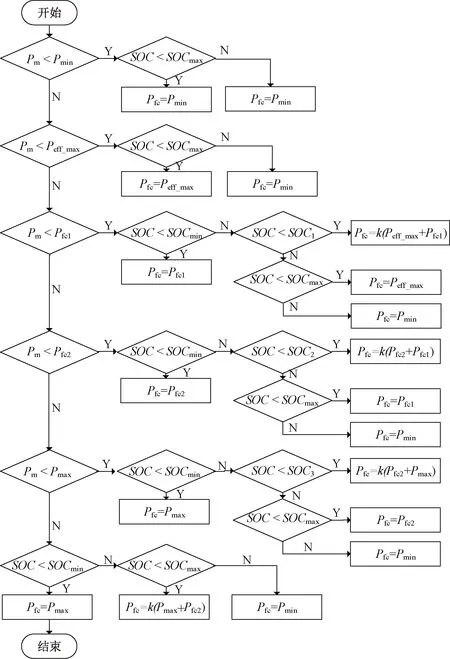
圖4 基于規(guī)則的功率分配策略流程圖

在該策略下,燃料電池有多個工作點。當(dāng)SOC值處于正常區(qū)間且較小時,燃料電池提供盡可能多的能量,以應(yīng)對后續(xù)可能會出現(xiàn)的大功率階段。當(dāng)SOC值處于正常區(qū)間且較大時,鋰電池提供盡可能多的能量,以防止后續(xù)可能會出現(xiàn)的制動狀態(tài),導(dǎo)致鋰電池過飽和。此外,燃料電池輸出功率的變化率對其壽命有著非常重要的影響,因此,本研究將燃料電池的最大變化率設(shè)定為5 kW/s,以降低燃料電池的壽命損耗。

2.2 多目標(biāo)白鯨優(yōu)化算法

為了降低系統(tǒng)氫耗并延長燃料電池壽命,用MOBWO進(jìn)行EMS參數(shù)優(yōu)化。該算法受到白鯨行為啟發(fā),建立了探索、開發(fā)及鯨魚墜落3個階段。

探索階段是通過人類飼養(yǎng)白鯨的行為記錄建立的。2只白鯨可以以同步或者鏡像的方式游泳。因此,白鯨的位置更新為

(12)

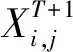
開發(fā)階段受到白鯨捕食行為的啟發(fā),白鯨通過分享彼此的位置信息來捕食,同時考慮捕食的最佳位置信息和其他白鯨位置信息。在開發(fā)階段引入了Levy飛行策略,以便于增強收斂性。其數(shù)學(xué)模型為

(13)

式中:r3、r4為(0,1)內(nèi)的隨機數(shù);C1為衡量Levy飛行強度的隨機跳躍強度;LF為Levy飛行函數(shù),其數(shù)學(xué)公式為

(14)

式中:u和v為正態(tài)分布的隨機數(shù);β取1.5;參數(shù)σ為

(15)

鯨落階段是考慮到白鯨在遷徙和覓食的過程中,少數(shù)白鯨收到自然界的威脅而死亡。其數(shù)學(xué)模型為

(16)

式中:r5、r6、r7均為(0,1)內(nèi)的隨機數(shù);Xstep為鯨魚墜落的步長,公式為

Xstep=(ub-lb)exp(C2T/Tmax)。

(17)

式中:C2為步長因子,與鯨魚墜落概率和種群規(guī)模相關(guān);ub和lb分別為變量的上邊界和下邊界。

2.3 基于白鯨優(yōu)化的能量管理策略

本文使用白鯨優(yōu)化算法對2.1節(jié)提到的基于規(guī)則的功率分配策略進(jìn)行參數(shù)優(yōu)化。其中,決策變量Xi=[Pfc1,Pfc2,Pfcmax,SOC1,SOC2,SOC3,k],目標(biāo)函數(shù)分別為等效氫氣消耗量和燃料電池的老化百分比:

(18)

算法中的參數(shù)設(shè)置如表3所示。

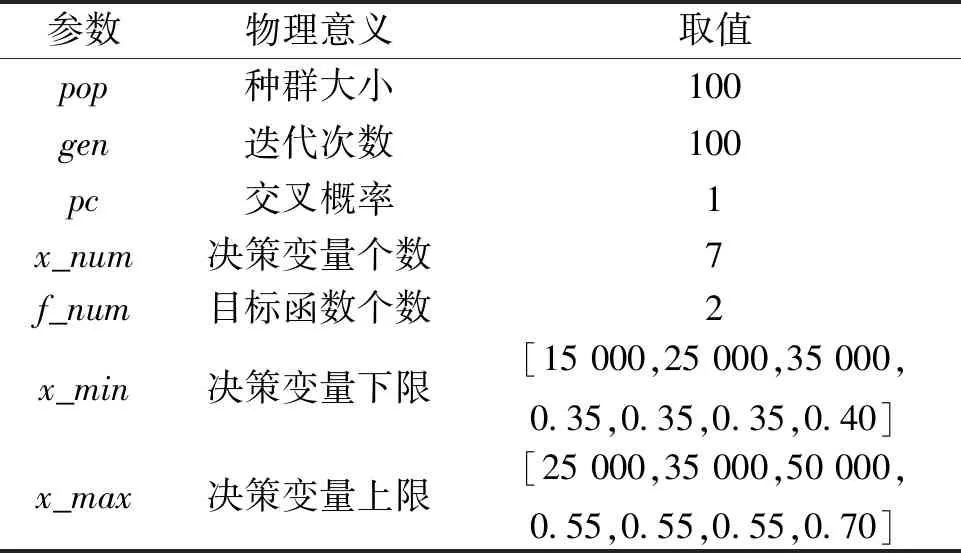
表3 白鯨算法參數(shù)

3 基于LSTM網(wǎng)絡(luò)的實時路況分類

駕駛路況判別是一個典型的分類問題,根據(jù)特定時間段的車速情況,可以將駕駛路況分為高速路況、暢通路況和擁堵路況。為了設(shè)計高精度的分類器,分別使用標(biāo)準(zhǔn)化城市駕駛工況(UDDS)、洛杉磯路況(LA92)及季節(jié)性制冷能效比路況(SC03)作為暢通路況集,曼哈頓城市路況(MANHATTAN)、城市擁堵路況(NYCC)作為擁堵路況集,主干線和高速行駛路況(US06)、未被空調(diào)滿負(fù)荷循環(huán)覆蓋的車輛工況循環(huán)(REP05)及美國乘用車高速公路燃油經(jīng)濟(jì)性測試工況(HWFET)作為高速路況集[24]。

本文使用LSTM神經(jīng)網(wǎng)絡(luò)來訓(xùn)練駕駛路況分類器的模型[25]。LSTM被認(rèn)為是循環(huán)神經(jīng)網(wǎng)絡(luò)(RNN)的變體,一般用來解決時間序列問題。其工作原理如圖5所示,A表示單個LSTM網(wǎng)絡(luò),LSTM將輸入序列x分成若干個時間步,每個時間步輸入一個向量,并根據(jù)當(dāng)前的輸入以及前面所有時間步的狀態(tài),計算出當(dāng)前時間步的輸出y。LSTM中的2個基本單元是記憶單元和門控單元。盡管LSTM比RNN網(wǎng)絡(luò)更加復(fù)雜,但是其門控單元使該網(wǎng)絡(luò)處理時間序列的效果更好。

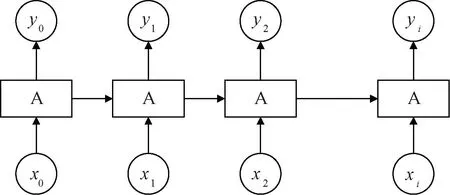
圖5 LSTM工作原理圖

本研究使用窗口大小為60 s的滑動窗口對不同駕駛路況的速度曲線取值,取得的一系列數(shù)據(jù)作為訓(xùn)練集。標(biāo)簽1為暢通路況、標(biāo)簽2為擁堵路況、標(biāo)簽3為高速路況。在對上述3種駕駛路況進(jìn)行LSTM網(wǎng)絡(luò)訓(xùn)練后得到駕駛路況分類器。其訓(xùn)練結(jié)果如圖6所示。由圖6可知,在訓(xùn)練1 000次之后,準(zhǔn)確度收斂至99.5%,滿足使用要求。

圖6 LSTM神經(jīng)網(wǎng)絡(luò)模型訓(xùn)練圖

4 實驗結(jié)果與分析

圖7展示了本文所提的EMS算法框架。首先,對燃料電池和鋰電池進(jìn)行離線測試,從而獲得關(guān)鍵參數(shù)并以此建立數(shù)學(xué)模型。其次,通過大量離線數(shù)據(jù)庫建立多目標(biāo)優(yōu)化策略和路況分類器,所提策略在MATLAB 2021b上實現(xiàn)。最后,通過獲取實時駕駛數(shù)據(jù)來進(jìn)行路況分類,并根據(jù)分類標(biāo)簽更新對應(yīng)的控制參數(shù)。本文算法基于MATLAB/Simulink平臺開發(fā),在優(yōu)化好控制器參數(shù)后,利用硬件在環(huán)仿真平臺進(jìn)行算法驗證,平臺架構(gòu)和設(shè)備參數(shù)如圖8所示。其中,實時仿真設(shè)備用于模擬混合動力系統(tǒng)的實際運行情況,并與EMS控制器進(jìn)行實時通信,在上位機界面監(jiān)控系統(tǒng)運行結(jié)果。

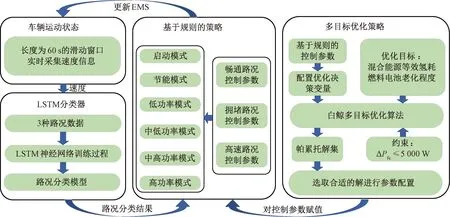
圖7 所提EMS算法框架

圖8 平臺架構(gòu)和設(shè)備參數(shù)圖

4.1 多目標(biāo)優(yōu)化結(jié)果

為了驗證所提策略的有效性,利用3種不同路況數(shù)據(jù)進(jìn)行仿真。經(jīng)過白鯨算法優(yōu)化參數(shù)后得到3組帕累托前沿,如圖9所示。在帕累托解中利用權(quán)重法和可行性法則共同挑選一組合適的最優(yōu)解作為基于功率分配的可變參數(shù),如表4所示。進(jìn)而,在該組參數(shù)下燃料電池與鋰電池的功率分配和SOC變化如圖10所示。由圖10可知,燃料電池能夠較平穩(wěn)地輸出功率。鋰電池提供峰值功率并及時吸收制動產(chǎn)生的能量,鋰電池的SOC在安全范圍內(nèi)波動。

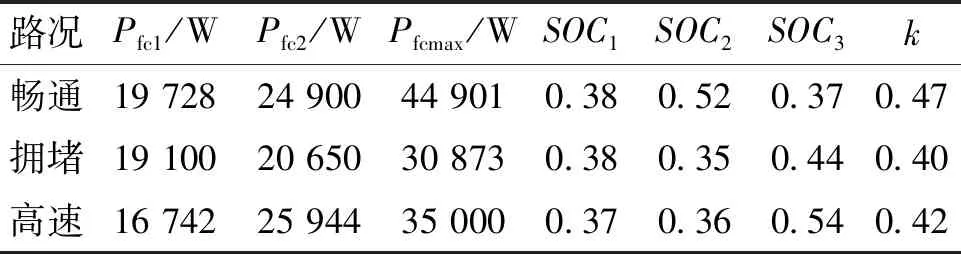
表4 多目標(biāo)白鯨算法優(yōu)化后的參數(shù)值

圖9 3類路況下的帕累托前沿

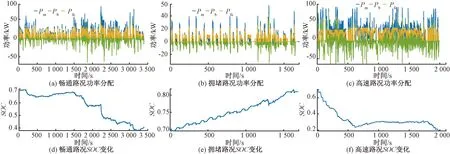
圖10 功率分配圖和SOC變化圖

4.2 基于LSTM分類器的實時功率分配策略

進(jìn)一步,為了研究所提方法的路況適應(yīng)性,利用全球輕型汽車排放測試工況(WLTC)作為測試工況。在每個行駛時刻采用其前60 s的速度值作為LSTM分類器的輸入,輸出則為標(biāo)簽的預(yù)測值。分類結(jié)果如圖11中黑色數(shù)字標(biāo)簽所示,在0～77 s時屬于暢通路況,78～244 s時屬于擁堵路況,245～1 627 s時屬于暢通路況,1 628～1 801 s時屬于高速路況。

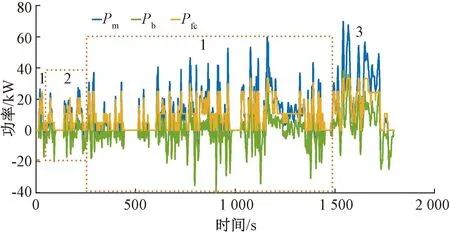
圖11 WLTC功率分配圖

圖11和圖12分別展示了在WLTC路況下的基于多目標(biāo)優(yōu)化和路況分類的功率分配結(jié)果和鋰電池的SOC變化曲線。從圖12中可以看出,基于多目標(biāo)和路況分類的EMS能夠?qū)崟r改變控制參數(shù),以應(yīng)對駕駛路況的改變。

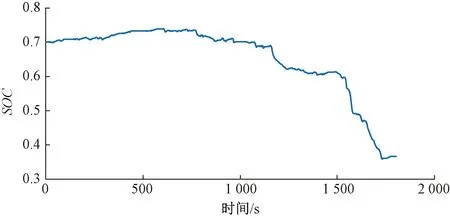
圖12 WLTC工況下的SOC

為了展示所提方法的優(yōu)越性,通過幾組與未優(yōu)化前的EMS結(jié)果進(jìn)行了對比分析,對系統(tǒng)的等效氫耗與燃料電池壽命衰減進(jìn)行了量化計算。表5展示了在WLTC工況下幾種不同EMS的氫氣消耗量和老化程度。其中,基于規(guī)則1、2、3表示根據(jù)設(shè)計者經(jīng)驗選取控制參數(shù)不同時的多模式功率分配策略。其決策變量分別為[12 000 35 000 50 000 0.5 0.5 0.5 0.5]、[12 000 35 000 45 000 0.5 0.4 0.4 0.5]、[20 000 40 000 50 000 0.5 0.5 0.5 0.67]。

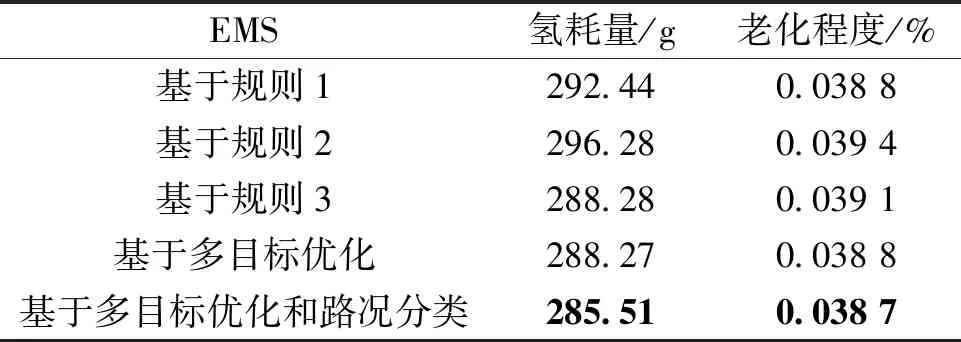
表5 不同EMS的氫耗量和老化程度

從表5可以看出,基于規(guī)則的控制參數(shù)取值的不同決定了EMS性能差異,需要依靠設(shè)計者經(jīng)驗來獲得最好的效果。基于多目標(biāo)優(yōu)化的EMS,針對單一路況能夠依據(jù)對氫氣消耗量和老化程度側(cè)重點的不同而選取最佳參數(shù)值,進(jìn)而得到符合自己預(yù)期的效果,基于多目標(biāo)優(yōu)化與基于規(guī)則1、2、3的均值相比,氫耗量降低了1.4%,老化程度降低了0.77%。基于多目標(biāo)優(yōu)化和路況分類的EMS能夠隨著路況的改變而改變功率分配的控制參數(shù),從而適應(yīng)于不斷變化的路況,基于多目標(biāo)優(yōu)化和路況分類與基于規(guī)則1、2、3的均值相比,氫耗量降低了2.3%,老化程度降低了1.02%。

5 結(jié)論

(1)針對混合動力系統(tǒng)能量管理問題,提出了一種基于多目標(biāo)優(yōu)化和路況分類的EMS。該策略引入等效氫耗模型和燃料電池的老化模型,并使用白鯨多目標(biāo)優(yōu)化算法對功率分配策略的控制參數(shù)進(jìn)行優(yōu)化。為了解決該策略不具有普適性的問題,引入了 LSTM神經(jīng)網(wǎng)絡(luò)對駕駛路況進(jìn)行分類。

(2)通過對3類經(jīng)典路況訓(xùn)練后得到了路況分類模型,用此模型將復(fù)雜測試路況分解成經(jīng)典路況,并在不同路況下實時轉(zhuǎn)換功率分配的控制參數(shù),以達(dá)到最優(yōu)效果。實驗結(jié)果表明,與未加入多目標(biāo)優(yōu)化和路況分類的策略相比,所提出的EMS具有較好的經(jīng)濟(jì)性和耐久性,并且能夠?qū)崟r改變策略以應(yīng)對變化的路況。

(3)混合動力系統(tǒng)的能量管理問題目前仍是一個較難的領(lǐng)域。所提出的EMS雖然表現(xiàn)出了良好性能,但是基于功率分配的EMS的局限性依舊存在。如何平衡車輛的動力性能、燃油經(jīng)濟(jì)性和動力元件的耐久性是未來一個重要的研究方向。