基于二階拋物線近似的結構可靠性分析方法

陳振中， 黃冬宇， 田 嬌， 李曉科， 吳子豪

（1. 東華大學 機械工程學院，上海 201620；2. 鄭州輕工業大學 機電工程學院，河南 鄭州 450002；3. 上海第二工業大學 智能制造與控制工程學院，上海 200135）

傳統的結構設計通常采用安全系數來保證產品達到預期的可靠度[1]。但是，安全系數過小會使結構可靠性過低，導致產品使用壽命不足；安全系數過大會使結構可靠性過高，導致產品生產成本增加。因此，為保證結構設計的合理性，開展可靠性分析是十分有必要的。

結構可靠性分析是指將結構尺寸、材料性能等各種不確定性因素視作隨機變量[2-3]，并根據隨機變量的分布來求解結構的可靠概率或失效概率。常用的可靠性分析方法主要分為2類：數值模擬法和近似解析法。其中，蒙特卡洛仿真（Monte Carlo simulation, MCS）法是最常用的數值模擬法[4-6]。該方法通過仿真、實驗得到大量樣本點對應的結構響應（如位移、載荷等），并統計失效樣本點數量與總樣本點數量的比值來得到設計點的失效概率，求解精度較高。但是，計算機仿真（如有限元仿真、流體仿真）及實驗的計算成本較高。

常用的近似解析法包括一階可靠性方法（first order reliability method, FORM）[7-8]和二階可靠性方法（second order reliability method, SORM）[9-10]。FORM 在最大可能點（most probable point, MPP）處對極限狀態函數進行一階泰勒展開。常用的FORM包括Hasofer等[11]提出的驗算點法和Rackwitz等[12]提出的當量正態化法。目前，FORM 已在眾多工程領域中得到廣泛應用。薛自然等[13]運用一次二階矩（first order second moment, FOSM）法對折臂機構的運動可靠度進行了研究；鄭財等[14]運用FOSM 法分析了三軸數控機床加工精度的可靠性；巴振寧等[15]運用改進的一次二階矩（advanced FOSM, AFOSM）法對埋地管道不同部位的失效概率進行了計算。然而，對于非線性可靠性問題，FORM的求解精度會降低。Chen等[16]在考慮FORM使用時最壞情況的基礎上提出了FORM的精度分析方法。由于極限狀態曲面在MPP處的曲率會對結構可靠性分析產生較大的影響，SORM通過對極限狀態函數進行二階泰勒展開來提高可靠性分析的精度，常用的SORM 為Breitung 方法[17-18]。相比于FORM，SORM 的求解精度得到了很大程度的改善。但Cai等[19]指出，Breitung方法的失效概率求解公式在特定情況下可能存在巨大的誤差，甚至會發生求解錯誤。

綜上，FORM雖然求解效率高，但其在以簡單的超平面代替復雜的極限狀態曲面時會造成精度損失；SORM的求解精度雖有所提高，但其近似公式可能會出現奇異解。為了解決上述問題，筆者擬提出一種基于二階拋物線近似的可靠性分析方法。該方法在SORM的基礎上以MPP作為拋物線頂點，根據極限狀態函數在MPP 處的曲率來構建近似拋物線，并通過求解拋物線極限狀態函數的可靠概率來代替原極限狀態函數的可靠概率，旨在為結構可靠性分析提供新思路。

1 可靠性分析方法基礎理論

1.1 一階可靠性分析方法

根據結構隨機變量的分布情況，結構的失效概率可表示為：

式中：Pf為結構的失效概率；g(x)為極限狀態函數，其中x為隨機變量，為隨機變量的概率密度函數。

在可靠性分析中，須將相關非正態分布的隨機變量x轉換為獨立的標準正態分布的隨機變量u。當利用FORM 計算式(1)時，在標準正態空間中將極限狀態函數g(u)在MPP 處進行一階泰勒展開：

其中：

式中：g(u)為標準正態分布下的極限狀態函數；uMPP為由MPP與坐標原點構成的向量。

極限狀態函數g(u)的可靠度指標β的幾何意義如圖1所示。由圖1可知，β為坐標原點到極限狀態函數的最短距離[20]。在二維可靠性分析中，FORM采用直線方程代替極限狀態函數，則極限狀態函數g(u)的失效概率可表示為：

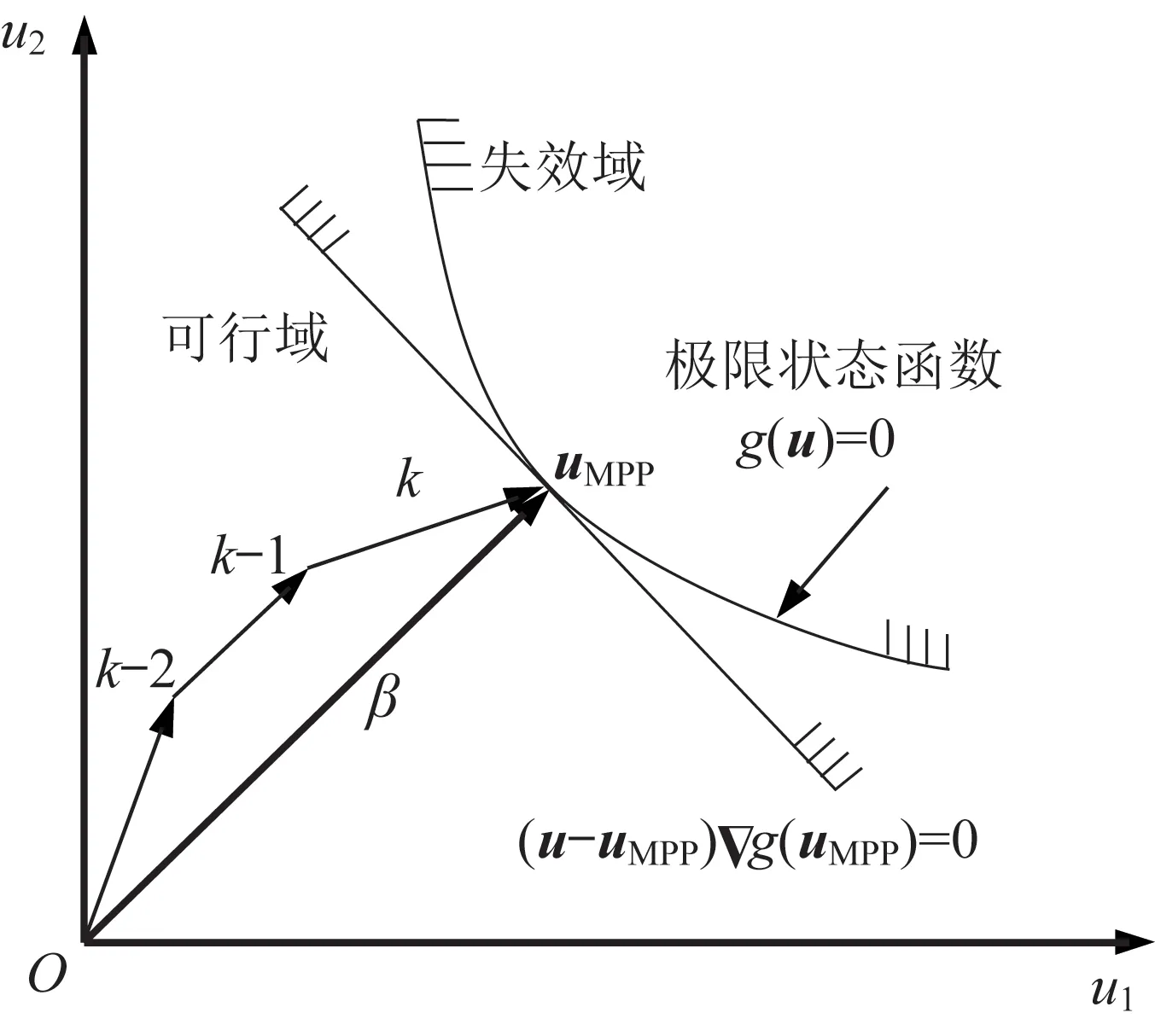
圖1 二維可靠性分析中的可靠度指標與MPPFig.1 Reliability index and MPP in two-dimensional reliability analysis

uMPP通常采用驗算點法來迭代求解，當β滿足精度要求時，最后一次迭代得到的向量uk即為uMPP。由此可得，基于驗算點法的β的迭代過程如下：

式中：βk為第k次迭代后對應的可靠度指標。

當極限狀態函數的非線性程度較低時，上述迭代過程可以穩定收斂；但當極限狀態函數為高度非線性時，迭代過程會因發生振蕩而難以收斂。Yang 等[21]通過引入混沌控制法（chaos control, CC）法來保證迭代過程收斂，即通過嚴格控制迭代步長來實現穩定收斂。引入CC 法后uk的迭代過程可表示為：

式中：λ為步長控制因子，C為單位矩陣。

當極限狀態函數為線性或遠離坐標原點時，利用FORM可以求解得到準確的結果。然而，當極限狀態函數的曲率較大時，FORM的近似值會與真實值產生較大偏差，此時須采用更精確的近似方法進行求解。

1.2 二階可靠性分析方法

SORM對極限狀態函數在MPP處進行二階泰勒展開時考慮了極限狀態函數的非線性程度。二階泰勒展開后的極限狀態函數可表示為：

式中：?2g(uMPP)為MPP處的Hessian矩陣。

令單位向量αu和Q分別為：

利用單位向量αu構造正交矩陣A，使ATA=I。正交矩陣A的表達式如下：

SORM 通過計算Hessian 矩陣來求解極限狀態函數在MPP處的主曲率，從而計算失效概率，具體公式如下：

其中：

式中：κi為第i個方向上的主曲率，eig(·)為矩陣的特征向量，(·)n-1為刪去第n行和第n列的n-1 階矩陣。

通常情況下，SORM在利用式(9)計算失效概率時須滿足βκi＜1，然而實際應用時并非總是滿足該條件。另外，當1-βκi的值過小時，會產生巨大的誤差。

2 基于二階拋物線近似的可靠性分析方法

2.1 拋物線方程的建立

通過上文分析可知，在二維情況下，當極限狀態函數呈高度非線性時，簡單地以直線方程代替極限狀態函數并不能滿足可靠性分析的精度要求，因此本文選擇在MPP處構建拋物線來近似表示極限狀態函數，如圖2所示。

圖2 二維可靠性分析中極限狀態函數的拋物線擬合與旋轉Fig.2 Parabola fitting and rotation of limit state functions in two-dimensional reliability analysis

根據定義，向量uMPP與FORM近似的極限狀態函數相互垂直，故以極限狀態函數的MPP為頂點，以向量uMPP為對稱軸建立拋物線。對于二維可靠性問題，只需1個主曲率即可確定一條拋物線；對于n維問題，則需n-1 個主曲率來確定所需的拋物線方程。如圖2(b)所示，將擬合得到的拋物線旋轉至u1軸上，由于標準正態分布函數具有軸對稱性質，旋轉后的拋物線與原拋物線具有相同的失效概率。由此可得，基于極限狀態函數MPP處曲率近似擬合的拋物線方程可表示為：

式中：ai為拋物線系數，由極限狀態函數在MPP處的主曲率κi確定，兩者的關系為-2ai=κi。

由此可得，最終結構的失效概率可表示為：

式中：φ(ui)為標準正態分布下的概率密度函數。

2.2 失效概率計算

如圖3 所示，在二維情況下，具有相同值的概率密度函數對應的幾何圖形為圓。令圓的半徑為ρ，則可將圓劃分為兩部分：一部分為位于拋物線外的可行域；另一部分為位于拋物線內的失效域。由角度比例可知，整個圓中失效域所占的比例為。則通過極坐標變化，式(11)可轉換為：

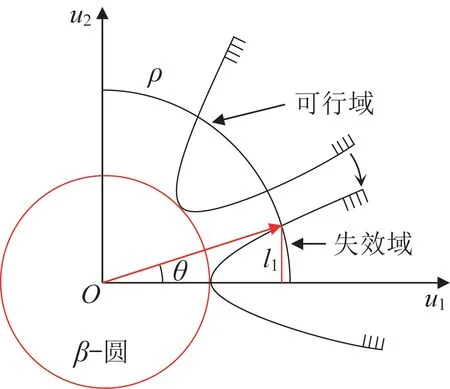
圖3 二維可靠性分析中可行域與失效域劃分示意Fig.3 Schematic of feasible and failure domain division in two-dimensional reliability analysis

其中：

式中：θ為拋物線與圓的相交點與坐標原點構成的向量與坐標軸之間的夾角。

在n維情況下，具有相同值的概率密度函數對應的幾何圖形為超球體。該超球體同樣可分為兩部分：一部分是拋物面外的可行域，另一部分是拋物面內的失效域。失效域的面積S可通過球面積分來求解，其表達式為：

式中：fui為f對ui的一階導數，其中f為超球面方程，f2+u21+u22+…+u2n-1=ρ2；V為投影區域，其為n-1維的超橢球體。

將式(14)轉換為以下形式：

基于坐標變換可將V從n-1維橢球體變為n-1維超球面，則式(15)可進一步轉換為：

在極坐標中，ui與ζi的轉換關系如下：

其中：

式中：l1、l2、…、ln-1為對應橢球體的短半徑。

根據計算得到的超球體與拋物面相交區域的失效域面積S，失效概率可視作失效區域面積與超球體面積的比值，即：

其中：

式中：Ss為超球體的面積。

3 實際算例

為了驗證本文所提出的基于二階拋物線近似的可靠性分析方法（下文簡稱為本文方法）的可行性以及準確性，結合3 個數值算例和1 個工程算例進行對比分析。采用本文方法對各算例進行可靠性分析，并與其他可靠性分析方法進行比較，包括FORM（選用CC法）、SORM（選用Breitung方法）和MCS法。

除了算例2 外，本文以MCS 法（樣本數為1×106個）直接仿真模擬計算得到的值作為精確值，再分別采用FORM、SORM和本文方法計算可靠概率Pr（Pr=1-Pf）并進行對比。

3.1 算例1

算例1中的非線性極限狀態函數g1(u)為：

式中：c、b為未知系數、參數。

極限狀態函數g1(u)中的變量u1、u2均服從標準正態分布且相互獨立，即u1～N(0,12),u2～N(0, 12)。極限狀態函數g1(u)的圖像如圖4所示。當g1(u)=0時，極限狀態函數g1(u)在標準坐標系下的圖形為拋物線，且所有拋物線均經過相同的頂點(b, 0)，拋物線頂點是與坐標原點距離最近的點，故β=b。

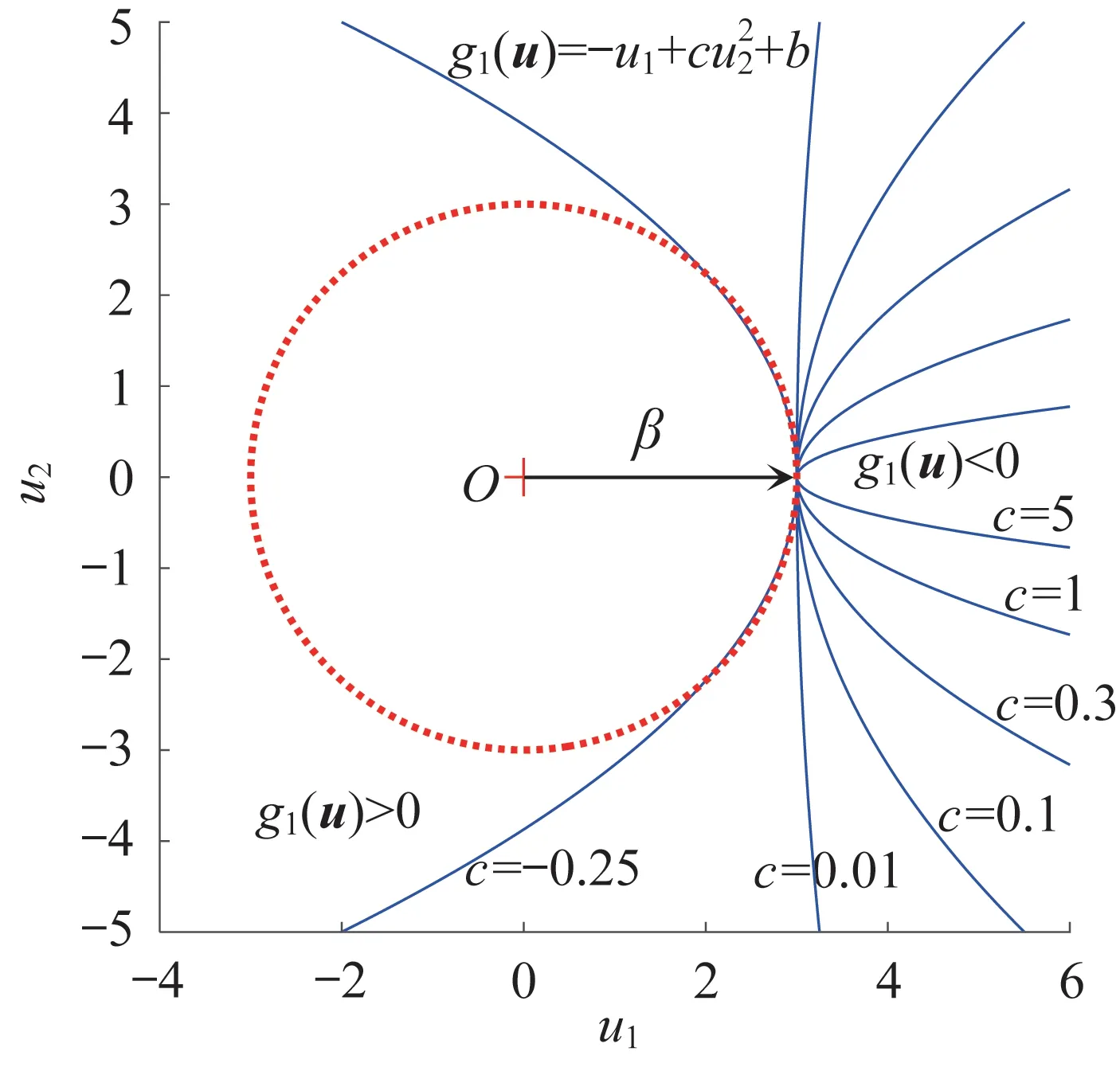
圖4 算例1的極限狀態函數Fig.4 Limit state function of example 1

需要注意的是，隨著極限狀態函數中系數c和參數b的改變，FORM 對極限狀態函數的近似結果始終為過拋物線頂點且與以b為半徑的圓相切的一條直線，不隨系數c的變化而變化；而SORM 對極限狀態函數的近似結果為過頂點(b, 0)的曲線，會隨著系數c的變化而變化。基于不同方法的算例1的可靠性分析結果如表1所示。由表1可知，在參數b相同、系數c不同的情況下，FORM 求解的可靠概率始終保持不變：當b=2 時，Pr=0.977 250；當b=3時，Pr=0.998 650。顯然，該結果對于不同的極限狀態函數來說是不合理的。當拋物線的非線性程度較高時，FORM與MCS法的可靠性求解結果的誤差較大。對于不同的系數，本文方法求解得到的可靠概率比SORM的精確，且與精確解幾乎一致。當取c=-0.25，b=2，3時，FORM 與MCS法的求解結果存在較大誤差。當取c=- 0.25，b= 3 時，由于曲率過大，使得βκ1≥1，因此采用SORM 的近似公式求解可靠概率時，產生了虛數解，導致求解發生錯誤；當取c=- 0.25，b= 2 時，由于βκi=1，SORM求解得到的可靠概率為無窮大，同樣發生求解錯誤。而本文方法在每種情況下均未發生求解錯誤，且求解得到的可靠概率與MCS法的求解結果相近，誤差較小。

表1 算例1的可靠性分析結果Table 1 Reliability analysis results of example 1

3.2 算例2

算例2為圓軸在隨機力矩下的可靠性分析。如圖5所示，圓軸的一端處于固定狀態，另一端受到外部力矩My、Mz（My、Mz的合力矩為M，M與y軸的夾角為ω）和扭矩T的作用。假設上述3個隨機變量服從相互獨立的標準正態分布， 即：My～N(μ1,δ21)，Mz～N(μ2,δ22)，T～N(μ3,δ23)，其中μi為隨機變量的均值，δi為隨機變量的標準方差。假設拉應力和剪應力（σx為x方向的拉應力，τxy′為xy′面的剪應力）在圓軸固定端A處達到最大。根據最大剪應力準則，可得極限狀態方程：

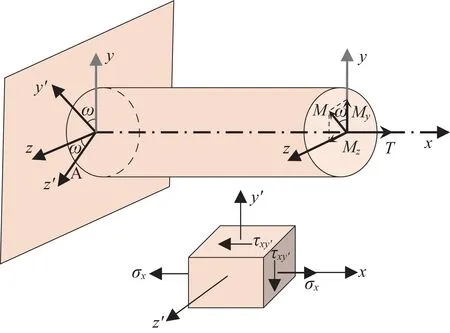
圖5 隨機力矩下的圓軸示意Fig.5 Schematic of circular axis under random torque

式中：Meq為作用在圓軸上的等效彎矩，[M]為許用彎矩，[σ]為許用應力。

假設上述3 個隨機變量的標準方差滿足δ1=δ2=δ3=δ，則可將外部力矩My、Mz和扭矩T標準正態化為變量u1、u2和u3，則式(23)可以轉化為：

由式(24)可知，g2(u)服從三自由度的非中心卡方分布，其非中心參數，故算例2 無需采用MCS 法進行仿真。根據非中心卡方分布的性質，可直接得到g2(u)的可靠概率Pr的真實解析解：

其中：

利用解析公式(25)、FORM、SORM 和本文方法對隨機力矩下的圓軸進行可靠性分析，結果如圖6所示。由圖6可知，隨著η的逐漸減小，SORM求解得到的可靠概率Pr與真實解析解之間的誤差逐漸增大，其求解精度甚至低于FORM，還出現了奇異解，因此不具有普適性。當采用本文方法求解可靠概率時，在η=2.5～3的情況下，其求解精度優于FORM和SORM，且本文方法在η≥3的情況下也能保證理想的精度。由此可知，本文方法在進行可靠性分析時更為穩定。

3.3 算例3

在算例3中，非線性極限狀態函數g3(x)為：

極限狀態函數g3(x)中各隨機變量的分布如表2所示。

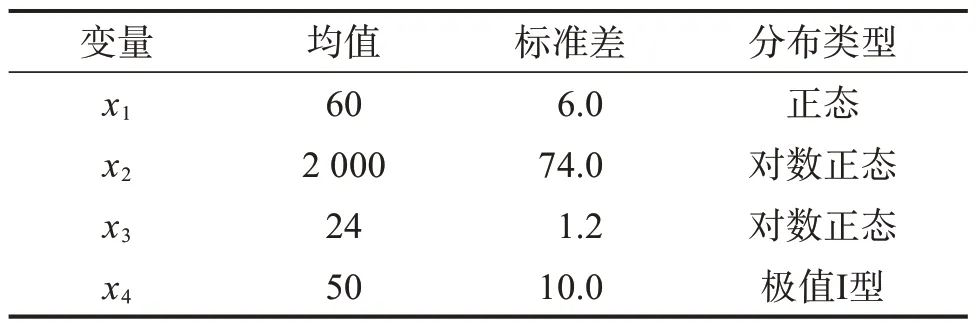
表2 算例3中隨機變量的分布情況Table 2 Random variables distribution of example 3

算例3中的隨機變量服從正態、對數正態和極值Ⅰ型分布，其可靠性分析結果如表3所示。由表3可知，與MCS 法相比，FORM 求解得到的可靠概率的誤差較大；SORM 求解時未發生錯誤，求解精度較高，SORM 求解的可靠概率與MCS 法的精確解之間的相對誤差為0.073 2%；當面向非正態分布的隨機變量時，本文方法的求解精度仍較高，與SORM 相比，本文方法求解得到的可靠概率的精度更高， 其與精確解的相對誤差僅為0.001 0%。

表3 算例3的可靠性分析結果Table 3 Reliability analysis results of example 3

3.4 算例4

算例4 為一個工程算例。如圖7 所示，該算例所分析的對象為一個對稱的屋頂桁架結構，其上桿為AD、DC、CF、FB，壓桿為DE、FG，底部桿為AE、EG、GB，張力桿為CE、CG。假設屋頂桁架的框架上承受了1個均勻分布的載荷q，將載荷q轉換為節點載荷。根據結構力學，節點C處桁架的垂直撓度W可表示為：

圖7 屋頂桁架結構示意Fig.7 Schematic of roof truss structure

式中：L為底部桿AE、EG、GB的總長度，Ac和As分別為鋼筋混凝土和鋼的橫截面積，Ec和Es分別為鋼筋混凝土和鋼的彈性模量。

鑒于W應滿足W≤0.03 m，則該屋頂桁架結構撓度的極限狀態函數可表示為：

式中：x=[qLAsAcEsEc]，所有隨機變量相互獨立，其分布如表4所示

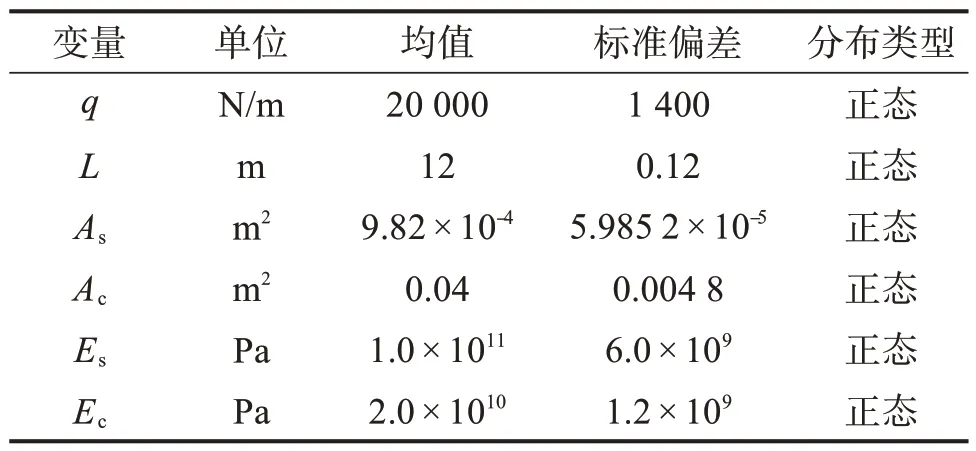
表4 算例4中隨機變量的分布情況Table 4 Random variables distribution of example 4

基于不同方法的算例4的可靠性分析結果如表5所示。由表5 可知，FORM 的求解誤差較大；本文方法的求解精度較高，優于SORM，由此驗證了該方法的可行性。

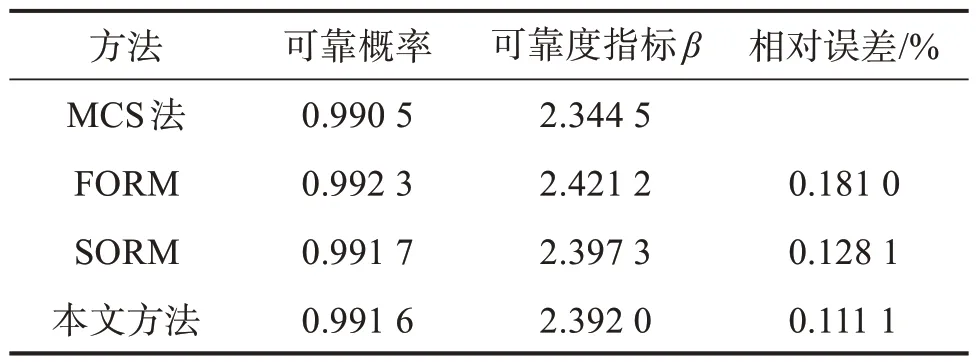
表5 算例4的可靠性分析結果Table 5 Reliability analysis results of example 4

4 結 論

1）本文利用CC法迭代求解了極限狀態函數的MPP，并根據極限狀態函數在MPP處各方向上的曲率來構建拋物線方程，以近似表示原極限狀態函數。結果表明，所構建的拋物線能夠很好地反映極限狀態函數在MPP處的邊界區域。

2）FORM 在求解非線性程度較高的極限狀態函數的可靠性時精度較低，SORM在特殊情況下會發生求解錯誤。通過3個數值算例和1個工程實例來比較FORM、SORM與本文基于二階拋物線近似的可靠性分析方法，對比結果驗證了所提出方法的有效性和可行性。

3）本文基于二階拋物線近似的可靠性分析方法要求解極限狀態函數的二階導數，計算量較大，具有一定的局限性。在下一階段，將進一步深入研究如何在減少計算量的同時提高可靠性的求解精度。