高中物理電學知識的解題技巧分析

陳小麗

(福建省三明市清流縣第一中學,福建 三明 365300)

高中物理電學部分的內容,具有實踐性與知識性雙線并進的特點,要求學生能夠熟練地掌握相關規律概念,并具有較強的電路分析能力.同時電學部分的考點較多且考查形式靈活,學生在解題時需要一定的解題技巧才能有效地提升做題速度與準確率.下面就高中物理教學中學生電學部分的易錯題型進行分析,并提出相對應的解題思路與技巧.

1 高中物理電學部分易錯題型

1.1 帶電粒子在電場中的運動問題

帶電粒子在電場中的運動相關題目的考查對學生來說是常見的易錯點,因為此類題目是一個綜合電場力和電勢能的力學問題,而且對學生來說做題難度比較大,且屬于易錯題型.

例1 某靜電場中的電場線如圖1所示,帶電粒子在電場中僅受電場力作用,其運動軌跡如圖1中虛線所示,由M運動到N,以下說法正確的是( ).

A.粒子可能是負電荷

B.粒子在M點的加速度大于它在N點的加速度

C.粒子在M點的電勢能大于它在N點的電勢能

D.由M運動到N的過程中電場力對該粒子做負功

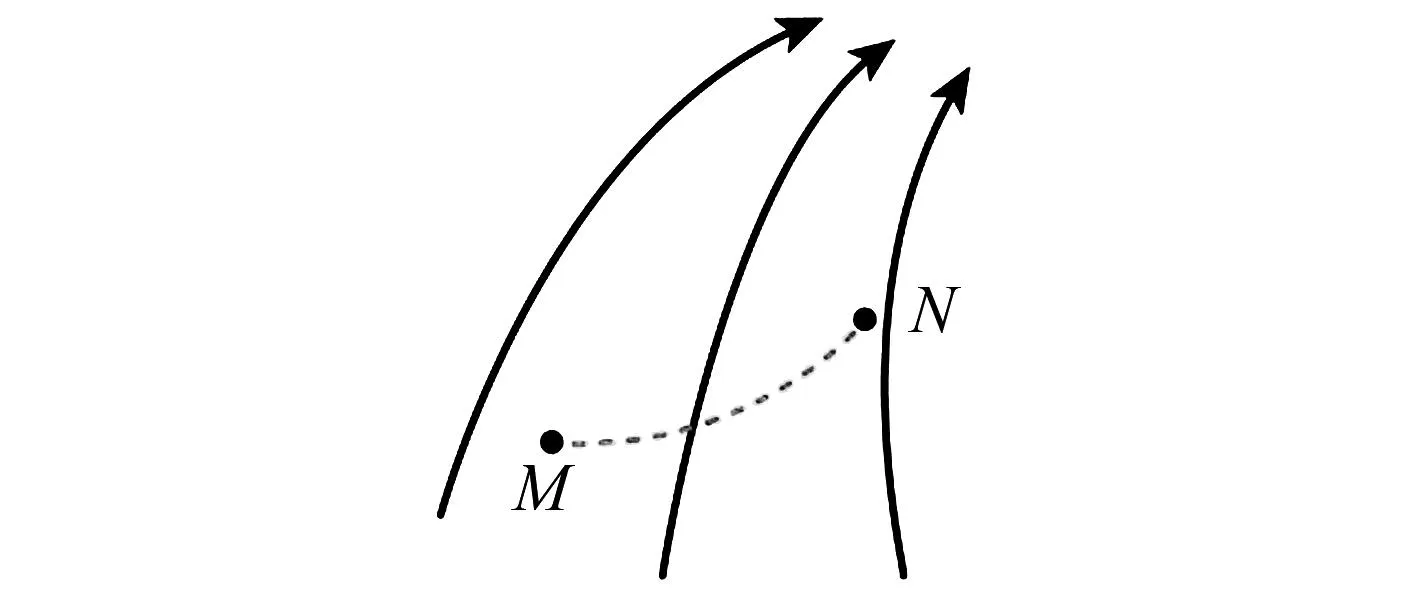
圖1 帶電粒子在電場中的運動軌跡

答案:C

1.2 磁場相關問題

在磁場相關問題中,學生容易混淆磁場強度和磁感應強度的概念,導致做題錯誤.

例2 如圖2所示,某時刻LC振蕩電路自感線圈L中電流產生的磁場的磁感應強度方向如圖2所示.下列說法正確的是( ).

A.若電容器正在放電,電容器上極板帶正電

B.若電容器正在充電,線圈中的磁感應強度也在增大

C.若磁場正在增強,電容器兩極板間的電場強度也在增大

D.若磁場正在減弱,則電場能也在減小

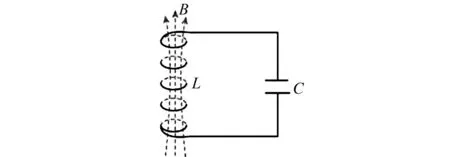
圖2 LC振蕩電路圖

本題考查磁場能轉化為電場能,線圈中的磁感應強度在減小,電容器正在充電.若磁場正在減弱,磁場能轉化為電場能,則電場能在增大.因此,對選項進行分析,A.若電容器正在放電,電路中電流減小,線圈中磁通量減小,根據磁感應強度的方向可知,回路中的電流為逆時針方向,則電容器上極板帶正電,A符合題意.

在解決這類問題時,學生需要明確兩者的概念“磁場強度是指單位磁極所受的磁場力,而磁感應強度是指單位面積垂直于磁場方向的磁通量.”并根據具體情況選擇合適的公式進行計算.此外,學生還容易忽略洛倫茲力的方向,導致計算結果錯誤.

1.3 以電磁感應為核心的綜合應用問題

在以電磁感應為核心的綜合應用問題中,學生容易忽略法拉第電磁感應定律的應用,導致解題出現錯誤.

例3 如圖3所示是法拉第研究電磁感應現象的實驗裝置,將兩個線圈繞在同一個鐵環上,線圈A與直流電源和開關S組成回路,線圈B與電流計組成閉合回路.當開關S接通的瞬間,電流計中有沒有電流通過?當開關S閉合,電路穩定后,電流計中有沒有電流通過?

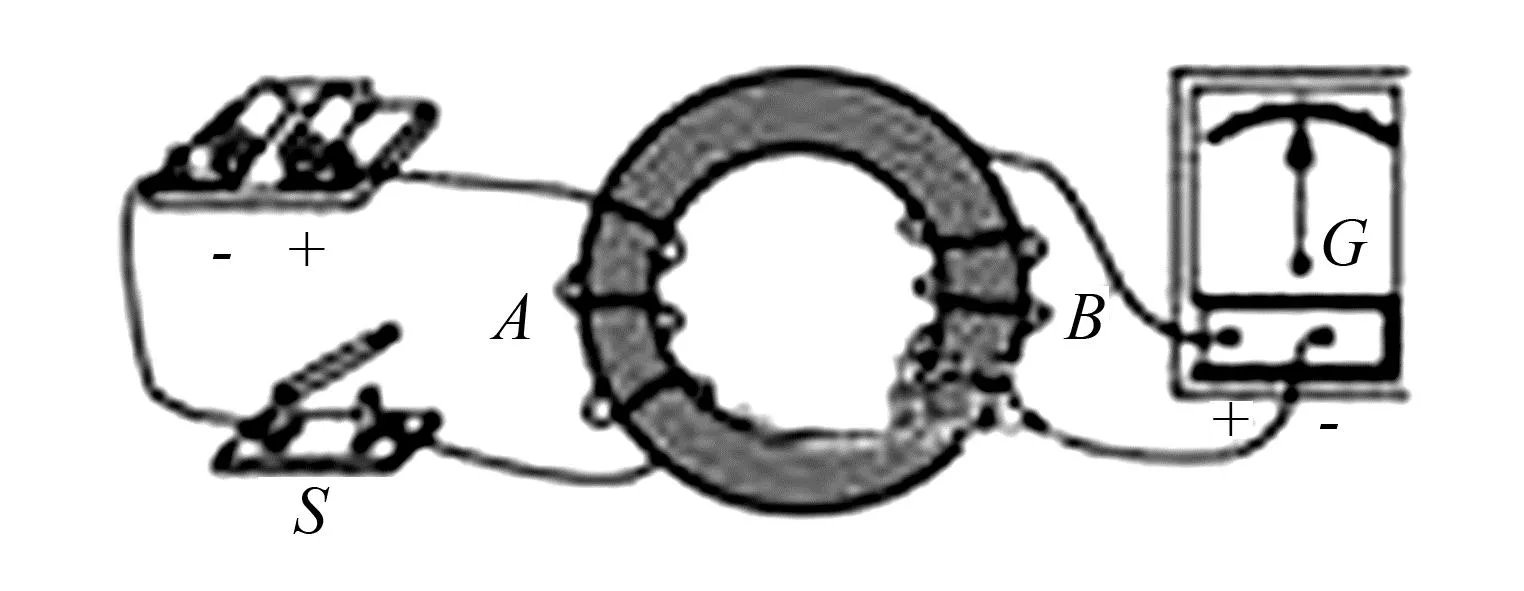
圖3 探究電磁感應現象實驗

本題考查的知識點是利用磁通量的變化可以判斷感應電流產生的條件.在本題中,當開關S接通的瞬間,A線圈中電流從無到有, 穿過B線圈中的磁通量發生變化,產生感應電流,根據楞次定律可知,感應電流從負極流入,指針向左偏.開關閉合穩定后,線圈B中磁通量不發生變化,不產生感應電流.

2 高中物理電學知識解題技巧研究

2.1 模型法解題技巧

模型法是一種化難為易解題方法.在解決電學問題時,學生能夠利用題目條件將復雜的電路轉化為簡單的電路模型[1],從而簡化問題的求解過程.此技巧的核心是通過審題將復雜的物理問題轉化為一個或多個自己熟悉的理想化物理模型,然后再運用自己熟悉的物理原理與規律解答題目.模型法的解題步驟為審題→分析→再現→建模→運算.

例4 如圖4所示,均勻帶電的圓弧AB帶電量為Q,其圓弧對應圓心角為240°.若已知其在圓心O點產生的場強為E0,若將其沿對稱軸切掉一半,只留下AC部分,則AC部分在圓心O點產生的電場強度大小為( ).

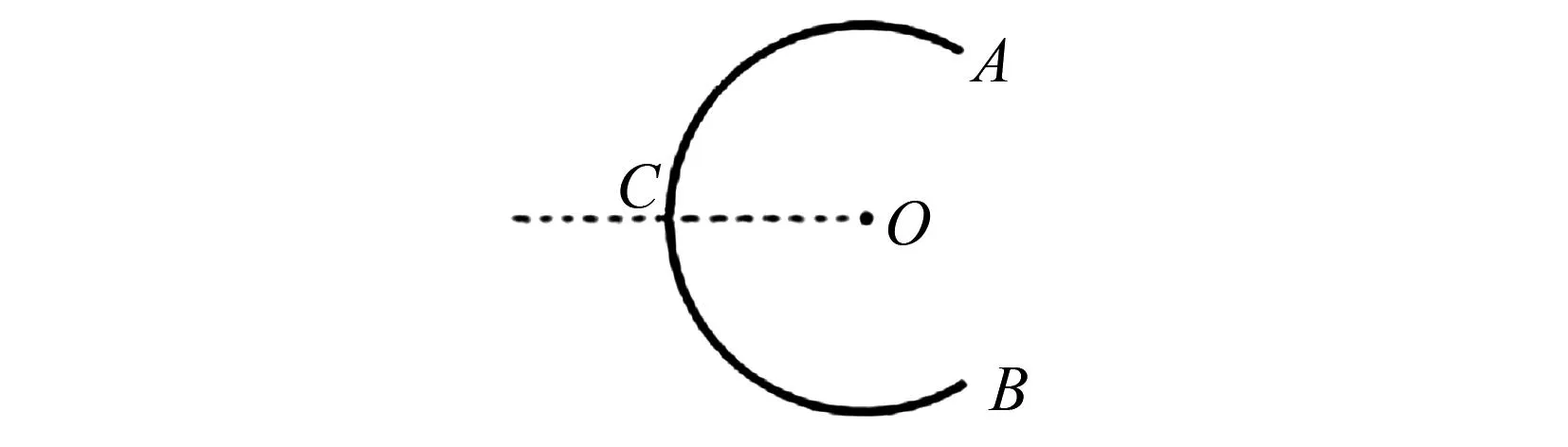
圖4 不規則帶電體

A.E0B.E0/2 C.E0/4 D.2E0/3

本題的難點是其形狀是一個圓弧,并非學生熟知的模型,因此在解題時通過審題觀察,學生可以采用模型法將題目構建成理想模型.具體來說,學生可以將圓環補全:即在AB之間補足一個圓心角為120°的均勻帶電圓弧,此時形成一整個圓.由于對稱性我們知道圓心O點的場強必定為0 ,再根據場強疊加原理我們知道補全部分在圓心的場強為-E0.(大小相等,方向相反).且巧妙的是,補全的部分恰好就是圓弧AB切掉一半以后的樣子,即補全部分與AC部分完全一致,所以AC部分產生的場強實際上就是E0,因此得出答案為A選項.

2.2 圖像法解題技巧

圖像法是一種通過圖像來解決問題的解題方法.比如,在解決電學問題時,可以通過畫出電路圖或者場線圖來幫助理解問題,從而更好地解決問題.在日常的做題中,教師可以引導學生適當的使用圖像法提升解題效率,在做題中從題目所給的圖像中提取有效條件,補充題目信息,提高做題準確率.

例5 如圖5(a)所示,電源的電動勢為E,內阻為r,R為電阻箱.圖5(b)為電源的輸出功率P與電流表示數I的關系圖像,電流表為理想電表,其中電流為I1、I2時對應的外電阻分別為R1、R2,電源的效率分別為η1、η2,輸出功率均為P0.下列說法中正確的是( ).

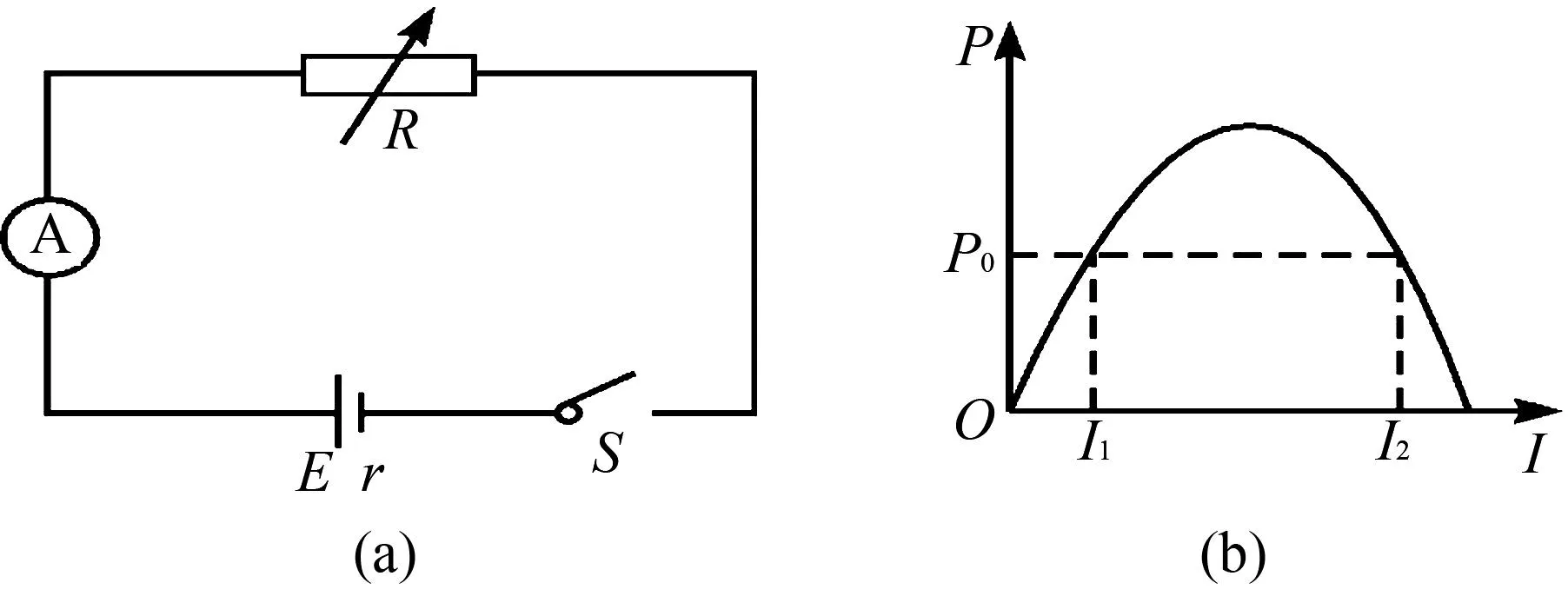
圖5 功率隨電流變化關系

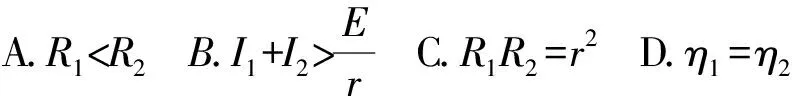
答案:C.

2.3 對稱法解題技巧

對稱法是一種通過對稱性來解決問題的方法,這種解題方法能夠有效地拓寬學生思路,讓復雜的問題變得更加簡潔.在解決電學問題時,可以通過電路的對稱性或者場的對稱性來簡化問題的求解過程.在實際的運用中,對稱法可以迅速準確地求解電場強度、帶電粒子在電場中的運動、帶電粒子在磁場中的運動、對稱電路等類型問題.在使用對稱法解題時,學生要注意審題,分析研究對象的屬性、運動規律、運動特點,尋找研究對象的對稱性特點,并依照物理規律進行求解[2].

例6 如圖6所示,帶電量為+q的點電荷與均勻帶電薄板相距為2d,點電荷到帶電薄板的垂線通過板的幾何中心.若圖中a點處的電場強度為零,根據對稱性,帶電薄板在圖中b點處產生的電場強度大小為____,方向____.(靜電力恒量為k).

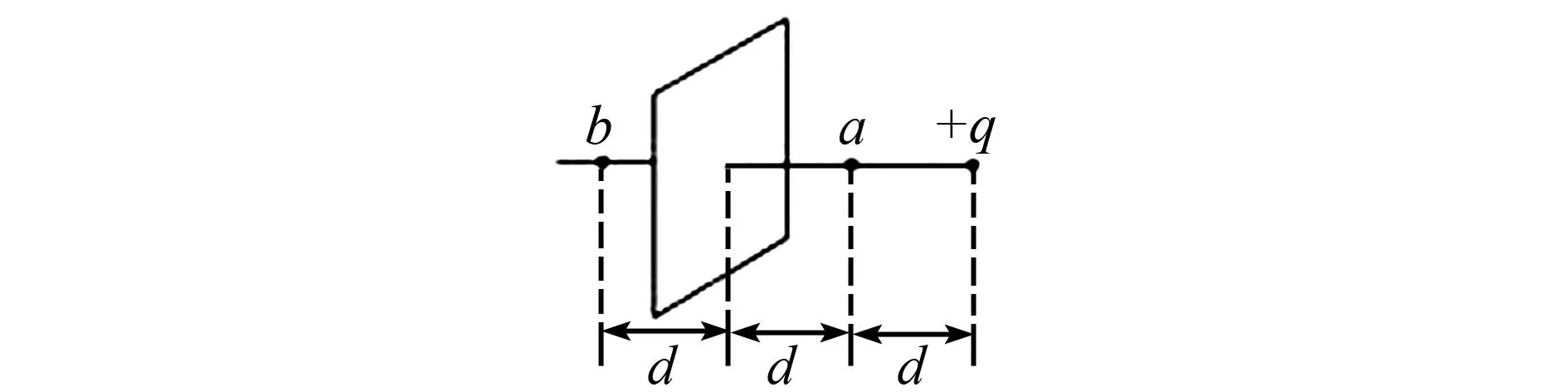
圖6 均勻帶電薄板的場強對稱性原理

本題主要考查的知識點為電場強度和電場線的相關內容,在解題時學生可以利用對稱法進行解題.本題的解題思路是利用電場強度的疊加結合對稱性去判別場強的大小和方向[3].因此,可以得出q在a點形成的電場強度的大小為E1=kq/d2, 方向向左,且因a點場強為零,故薄板在a點的場強方向向右,大小也為kq/d2,再由對稱性可知薄板在b點的場強是kq/d2,方向向左.

2.4 等效法解題技巧

在解決電學問題時,等效法可以將復雜電路轉化為等效電路,從而簡化問題的求解過程.在做題時,學生要明確題目中由哪些條件與范圍可以進行等效轉換.等效法解題一般涉及物理等效、物理模型等效、物理過程等效三種,靈活利用等效法解題技巧有利于提升學生的變通意識、明確解題思路.

3 結束語

總之,在高中電學部分的教學中,教師可以采用模型法、圖像法、等效法、對稱法、極端法等解題技巧幫助學生解題,讓電學部分較為抽象的知識點變得較為容易理解,逐步提升高中生解題水平.