學(xué)會(huì)思考 把握本質(zhì)
——以2023年高考數(shù)學(xué)全國(guó)乙卷理科第11題為例*

姚愛亮

(江蘇省鹽城市第一中學(xué) 224005)

2023年全國(guó)乙卷理科第11題是一道圓錐曲線中點(diǎn)弦問題,條件簡(jiǎn)潔,背景熟悉,主要涉及直線與雙曲線相交、弦中點(diǎn)等,解決的方法往往采用數(shù)形結(jié)合思想、點(diǎn)差法、“設(shè)而不求”的方法和韋達(dá)定理.

1 試題呈現(xiàn)

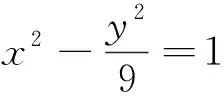
A．(1,1) B．(-1,2)

C．(1,3) D．(-1,-4)

2 試題解析

解法1——“小題大做”[1]

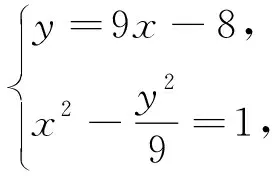
對(duì)于選項(xiàng)C,可得kOM=3,kAB=3,則直線AB的方程為y=3x,而雙曲線的漸近線為y=±3x,所以直線AB與雙曲線沒有交點(diǎn),故C錯(cuò)誤．

顯然“小題大做”運(yùn)算大,耗時(shí)長(zhǎng),而且容易出錯(cuò),在考場(chǎng)上應(yīng)謹(jǐn)慎使用．

解法2——“小題小做”

學(xué)生對(duì)圓錐曲線中弦的斜率與弦中點(diǎn)之間的關(guān)系是熟悉的,解法2借助雙曲線漸近線這一幾何特征線,抓住直線與雙曲線相交時(shí)直線的斜率與漸近線斜率之間的大小關(guān)系,進(jìn)而得到弦坐標(biāo)中點(diǎn)的條件,從而很快鎖定正確選項(xiàng)．

3 回溯本源

解(1)當(dāng)過點(diǎn)P的直線l的斜率不存在時(shí),若l與雙曲線相交于A,B兩點(diǎn),且點(diǎn)P為弦AB的中點(diǎn),根據(jù)雙曲線的對(duì)稱性可知,顯然只有點(diǎn)P在x軸上,此時(shí)以點(diǎn)P(x0,0)(x0>a,x0<-a)為中點(diǎn)的弦AB所在的直線l是唯一存在的．

圖1

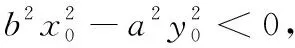
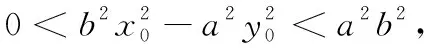
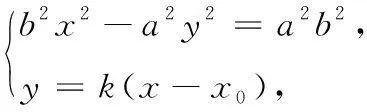
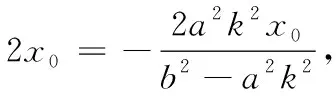
在教科書中也可以找到類似的問題:

4 結(jié)束語

2023年,教育部考試中心命制的六套高考數(shù)學(xué)試卷難度較去年均有所降低,但保持試題靈活性不變、創(chuàng)新性不變,突出強(qiáng)調(diào)對(duì)基礎(chǔ)知識(shí)和基本概念的深入理解和靈活掌握,注重考查學(xué)科知識(shí)的綜合應(yīng)用能力,科學(xué)引導(dǎo)中學(xué)教學(xué),促進(jìn)考教銜接.作為一名數(shù)學(xué)教師,課堂教學(xué)中應(yīng)注重知識(shí) 產(chǎn)生的過程,注重?cái)?shù)學(xué)學(xué)科的本性原法,教會(huì)學(xué)生如何思考問題,促使學(xué)生將知識(shí)和方法內(nèi)化為自身的知識(shí)結(jié)構(gòu),把握問題本質(zhì),以不變應(yīng)萬變, 以使學(xué)生在高考考場(chǎng)上能迅速找到解決問題的突破口[4].