帶有刪失函數型協變量的非參數模型的估計研究
李 響,王純杰,盧哲昕,徐 萍
隨著技術的進步,函數型數據分析在越來越多的領域中發揮著重要作用,如醫學、生物學、經濟學等領域.由于觀測對象在試驗中需要長期隨訪,因此,每個觀測對象的生理指標的測量結果通常被記錄為曲線的形式,并且由于觀測對象加入試驗、退出試驗的時間不一致或者中途退出導致的差別、觀測時間的局限性或客觀條件的限制等因素的影響,人們通常不能得到完整的觀測曲線.例如在醫學研究中許多數據集是通過患者定期檢查并記錄下來,然而患者忘記檢查或者醫療設備的損壞都可能產生刪失函數型數據.目前對于刪失函數型數據已經有學者進行了研究,例如DELAIGLE 等[1]使用曲線擴展算法對刪失函數型數據進行擴展.DELAIGLE 等[2]提出使用馬爾科夫鏈的方法對刪失函數型數據進行擴展.KRAUS 等[3]提出正則化方法對不完整的函數型數據進行分類.DELAIGLE 等[4]通過計算張量級數的方法得到協方差函數并且得到近似完整的函數型數據.DESCARY等[5]對規則密集的數據提出使用矩陣補全方法重新構造協方差函數.LIN 等[6]針對刪失函數型難以計算非對角線區域的信息問題,使用基函數展開的方法估計協方差函數.LIN等[7]把協方差函數分解為方差函數分量和相關函數分量來解決刪失函數型的協方差函數不好估計的問題.趙志文等[8]在缺失數據下使用均值補充法、條件均值補充法研究了區間自回歸模型的參數估計問題.
非參數回歸模型具有回歸函數形式靈活、適應性廣泛的優勢.FERRATY 等[9]在非參數模型下把核估計應用于函數型數據和時間序列數據.RACHDI 等[10]對非參數模型估計中的帶寬選擇進行研究.MOHAMMED 等[11]在非參數模型下針對函數型協變量,使用核估計方法解決魯棒回歸問題.FLORENT 等[12]提出使用k近鄰方法估計非參數模型.王景樂[13]在刪失指標隨機缺失下研究回歸函數的非參數估計.孟書宇[14]使用k近鄰方法估計相依函數型非參數模型.程彥茹[15]使用k近鄰方法估計隨機缺失函數型非參數模型.
本文研究具有刪失函數型協變量的非參數模型的估計問題.使用曲線擴展算法把刪失函數型數據擴展至完整數據.通過建立非參數模型,可以得到函數型協變量對標量響應變量的預測.通過模擬研究驗證該方法的有效性,并應用到肝硬化數據集.
1 模型與估計
在實驗過程中人們往往以函數型數據的形式來記錄試驗結果,但由于各種因素不能觀測到函數型數據的全部過程,因此產生刪失函數型數據.假設觀測數據為Xi(t) ≡Xi,i=1,…,n,每條觀測數據Xi(t) 只能在部分區間Ii=[ai,bi]可被觀測到,且Ii?I0,其中ai和bi分別表示第i個樣本的左端點和右端點,I0表示完整觀測的區間.例如文獻[1]研究了8 歲到25 歲四個種族群體(亞洲人、黑人、西班牙人和白人)脊柱骨密度分類問題,其中對每個個體只能進行2 次到4 次的測量,只觀測到部分區間內的部分函數型數據.像這種觀測次數不同、觀測時間不同的函數型數據,不經過處理很難建立模型.本文將介紹一種非參數的方法對刪失函數型數據進行擴展,并建立非參數模型.非參數模型定義為:
式中:Yi為標量響應變量,r(?)為未知的非線性算子,εi為滿足E(εi|Xi)=0 的隨機誤差,Xi為刪失函數型數據.
在建立模型前需要通過曲線擴展算法把刪失函數型數據進行處理.本文使用的方法為文獻[8]中的函數型核估計方法,公式如下:
式中:wn,h(?,?)為權重函數,可以表示為:
式中:K(?)為核函數,d(?,?)為半度量,h為窗寬,在進行估計時需要對核函數、半度量和窗寬h進行選擇.
2 刪失函數型數據擴展算法
本文使用文獻[1]提出的基于垂直距離將刪失函數型數據擴展為完整函數型數據的方法.該方法具有計算快、精確度高、靈活性高、非參數等優勢.具體過程為,假設觀測到的樣本為在區間Ishort=[ashort,bshort]上的函數型數據Xshort,其中ashort和bshort分別表示需要擴展的函數型數據的左端點和右端點,使用區間Ilong=[along,blong]?Ishort上的數據Xi,i=1,…,n估計Xshort未觀測到的部分,并且Ishort?Ilong?其中along和blong分別表示長于數據Xshort的左端點和右端點.從bshort的右邊來構造擴展數據Xext的具體算法步驟如下:
步驟1:設置對于所有的t∈[ashort,bshort],使Xext(t)=Xshort(t)且j=1,j為擴展的次數,bext,j=bshort.
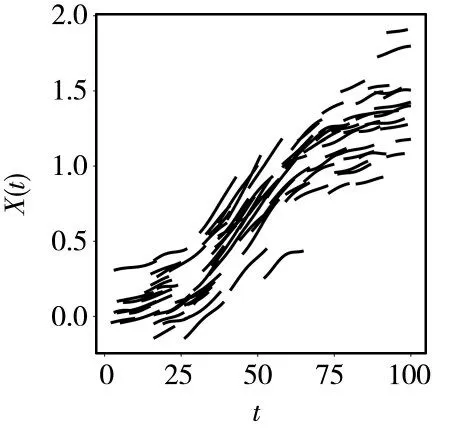
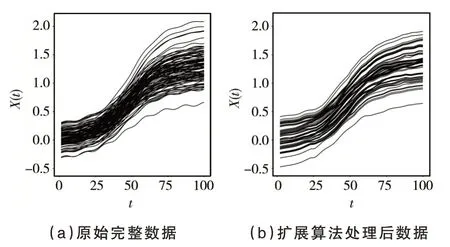
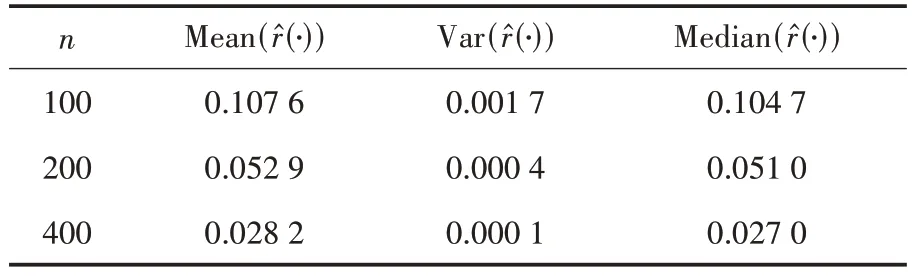
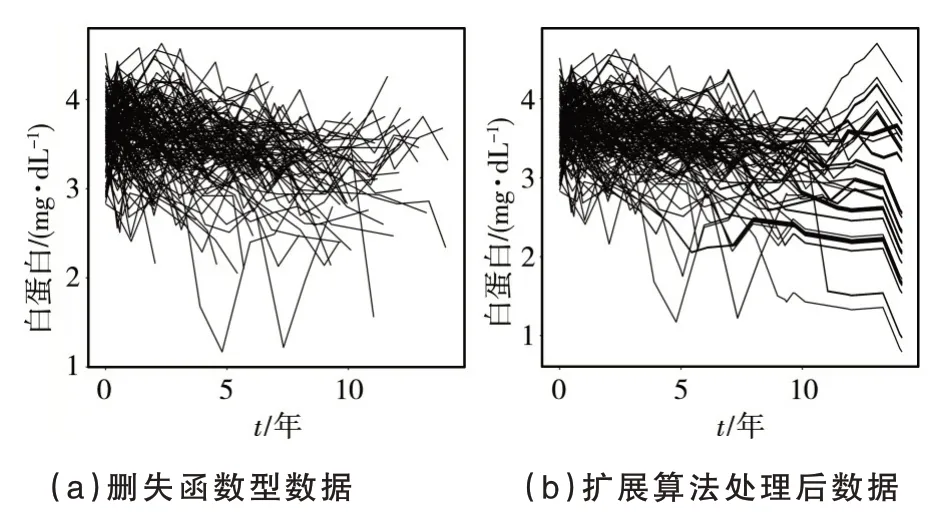
步驟2:對于j=1,2,…,重復以下步驟直到bext,j (1)找到所有滿足ai≤bext,j和bi>bext,j的函數型數據Xi,選擇它們其中的一個命名為Xi*,Xi*被觀測在Ii*=[ai*,bi*],其中ai*和bi*分別表示函數型數據Xi*的左端點和右端點. (2)擴展出的右端點bext,j+1=min(bi*,blong,bext,j+Δ),其中Δ >0 是調優參數. (3)對于每個t∈[bext,j,bext,j+1],使Xext(t)=Xi*(t) ?Xi*(bext,j)+Xext(bext,j). 在實踐中,該算法需要在步驟2 的(2)中對調優參數Δ 進行選擇,Δ 的作用是為了防止擴展過長的函數型數據片段使擴展函數型數據產生較大的誤差.為了擴展數據片段Xext足夠短,并且擴展的數據片段盡可能包含I0上出現的特征模態、凹凸度變化的小片段.可以設置Δ=|I0|/10,其中|I0|表示I0的長度.如果函數型數據具有快速變化的特征,Δ 可以取的更小. 算法中還需要在步驟2 的(1)中選擇確定函數型數據Xi*.假設在步驟2 的(1)中有cj個滿 足ai≤bext,j和bi>bext,j的函數型數據Xi,i=c1,…,cj.以下是選擇函數型數據Xi*的兩個方法. 方法一是在cj個碎片中隨機獲得函數型數據Xi*,每一個被選擇的概率為pij=1/cj.當數據Xi*與來自總體的完整函數型數據的樣本具有相同的主要屬性時,可以使用這個方法.方法二是當一組函數型數據有明顯的形狀相似時,每條函數型數據的形狀在局部與附近數據的形狀相似.在這種情況下,可以通過選擇使用最近的刪失函數型數據的方式.更具體地說,假設感興趣的是在bext,j的右邊擴展數據Xext,讓D(Xi,Xext;bext,j) 表 示Xi和Xext在點bext,j的距離.刪失函數型數據的形狀取決于它們局部垂直軸上的位置距離,讓D(Xi,Xext;bext,j)=|Xi(bext,j)?Xext(bext,j)|,可以得到 同樣的算法可以應用在函數型數據的左側,通過與上面相同的方式從右向左每次擴展一小段.使用這種非參數的方法可以把刪失函數型數據擴展為完整的函數型數據. 下面將通過數值模擬來驗證文中所給模型與算法的可行性.定義非參數模型為: 設置εi~N(0,1),函數型協變量為: 設置每條刪失函數型數據只有在區間Ii=[Ai,Bi]上可以被觀測到,其中Ai=[Ui],Bi=min(Ai+[Vi],100),Ui~U[1,95],Vi~U[7,15].上述設置模擬100 個刪失函數型樣本數據圖如圖1 所示. 圖1 刪失函數型數據 圖1 中隨機生成的100 個刪失函數型數據原始完整數據與擴展算法處理后數據的對比圖如圖2 所示.使用垂直距離最小的方法將刪失函數型數據盡可能表現出完整數據的特征,其中圖2(a)為原始完整數據,圖2(b)為使用曲線擴展算法補充后的數據,設置調優參數Δ=10. 圖2 刪失函數型數據原始完整數據與擴展算法處理后數據對比圖 從圖2 可以看出,使用該算法處理過的函數型數據可以近似地表現出原始函數型數據的特征. 在估計非參數模型時,選擇半度量為 使用正態核函數和Nadaraya?Watson 類型的窗寬并且通過廣義交叉驗證程序選擇最優窗寬為s=2.通過使用計算的均方誤差的均值、中位數、方差對進行評價的均方誤差表示為: 在上述設置下循環200 次,樣本量分別為100、200、400,非線性算子的均方誤差的均值(Mean())、方 差(Var())、中位數(Median())評價指標如表1 所示. 表1 非線性算子均方誤差的均值、方差、中位數 表1 非線性算子均方誤差的均值、方差、中位數 下面采用非參數模型對原發性膽汁肝硬化數據進行分析,由于不可控制的因素,所以每位患者的觀測時間和觀測次數都不同.本實例使用觀測樣本n=150 進行建模,研究白蛋白對血清膽紅素的影響.設置調優參數Δ=1.5,使得刪失指標白蛋白擴展至區間[0,14]. 設置模型血清膽紅素為響應變量Yi,i=1,…,150,白蛋白為函數型協變量且Yi=r(Xi)+εi,i=1,…,150. 在估計時采用半度量d2(Xi,Xj)=采用正態核函數和Nadaraya?Watson 類型的窗寬h,并通過廣義交叉驗證得分來進行選擇最優窗寬.具體如圖3所示. 圖3 刪失函數型數據與使用擴展算法處理后數據對比圖 從圖3 可以看出,肝硬化患者隨著患病時間的延長,白蛋白會呈現下降趨勢. 圖4 的分布情況 本文通過曲線擴展算法可以將刪失函數型數據擴展至完整函數型數據,在建模時避免了刪失函數型數據對模型的影響.通過對非參數模型中非參數算子的估計,驗證估計值的相合性和穩定性.本文通過模擬數據和實例數據驗證曲線擴展算法的實用性和準確性. 在曲線擴展實踐中,當樣本量n很小時,曲線會擴展到越來越大的區間,誤差也會變大,所以曲線擴展算法樣本量不能太小,并且在算法中需要曲線Xi,i=1,…,n覆蓋I0大部分區間,如果在I0出現數據曲線沒有覆蓋到的地方,程序將無法運行.如果Xi在某一小部分區間刪失的數據比較少,在數據擴展時會將大量的擴展數據集中使得誤差變大,這也是后續要改進的問題.在曲線擴展中需要對參數Δ 進行選取,如果參數Δ 過大會使擴展后的曲線不能展示出I0上曲線的特征;如果參數Δ 過小首先會出現的問題是影響數據曲線整體的走勢形態,其次是會極大增加不必要的計算量,運行速度降低.因此,調優參數Δ 的精確選取有待進一步研究.3 數值模擬
4 實例分析
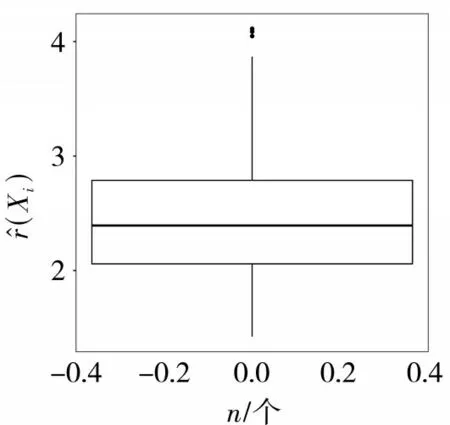
5 結語

