等腰三角形的存在性問題探究

摘? 要：等腰三角形是初中數學中常見的一類特殊三角形，其與拋物線相結合的存在性問題是中考的熱點問題，也是難點問題，具有一定的選拔功能.在初中數學教學中，可借助網絡畫板進行實驗探究，讓點動起來，讓學生在形象且直觀的現實情境中理清已知條件與所求結論之間的邏輯關系，然后引導學生利用所學知識給出問題的求解方法.

關鍵詞：等腰三角形；拋物線；動點；存在性問題

中圖分類號：G632??? 文獻標識碼：A??? 文章編號：1008-0333（2024）02-0011-03

收稿日期：2023-10-15

作者簡介：郎春林（1982.2-），男，江蘇省揚州人，本科，中學二級教師，從事初中數學教學研究.

存在性問題是指根據數學問題所給定的已知條件，探究是否存在符合要求的結論.存在性問題是探索型數學問題中一種非常典型的問題，其探索的方向是明確的，探索的結論有兩種，即存在或不存在．與等腰三角形有關的存在性問題倍受命題者的青睞，等腰三角形與拋物線相結合的存在性問題在中考試題中經常出現，其具有一定的難度，“兩圓一線定位置，邊角相等分類列”是解決這類問題的基本思路與方法.本文以2017年貴州省安順市中考的拋物線試題為例，呈現這類問題的求解思路，以期提高學生的解題能力.

1 問題呈現

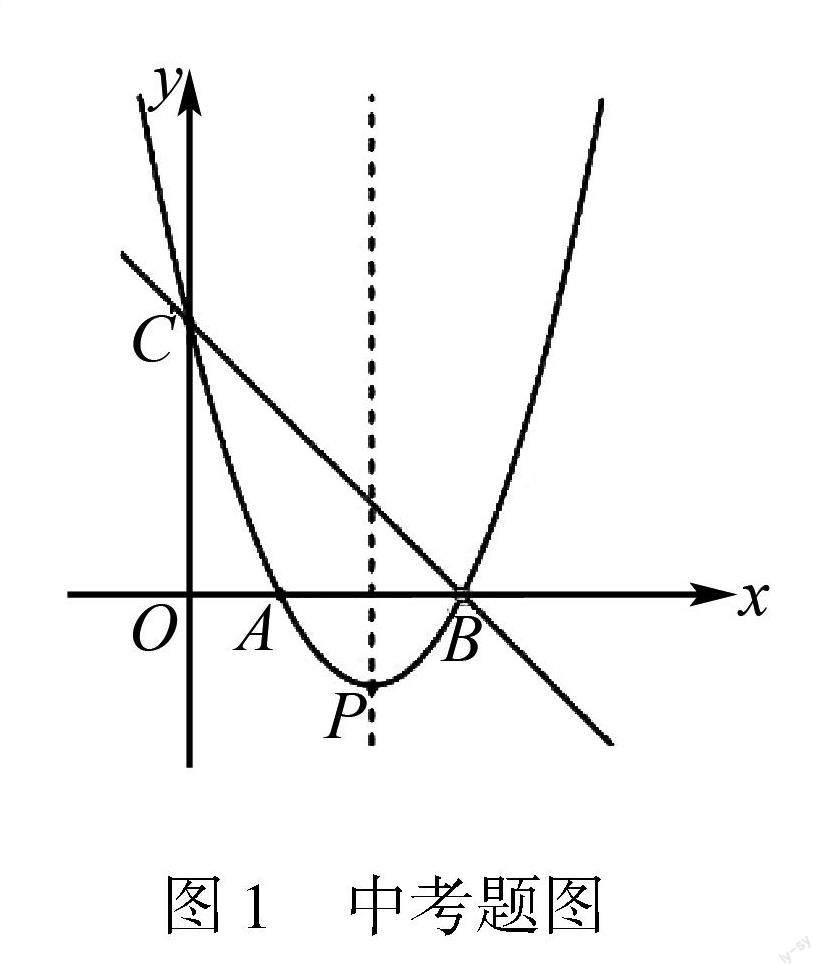
（2017年貴州省安順市中考數學第26題）如圖1，直線y=-x+3與x軸、y軸分別交于B，C兩點，經過B，C兩點的拋物線y=x2+bx+c與x軸的另一個交點為A，頂點為P.

（1）求該拋物線的解析式.（2）在該拋物線的對稱軸上是否存在點M，使以C，P，M為頂點的三角形為等腰三角形？若存在，請直接寫出所有符合條件的點M的坐標；若不存在，請說明理由.

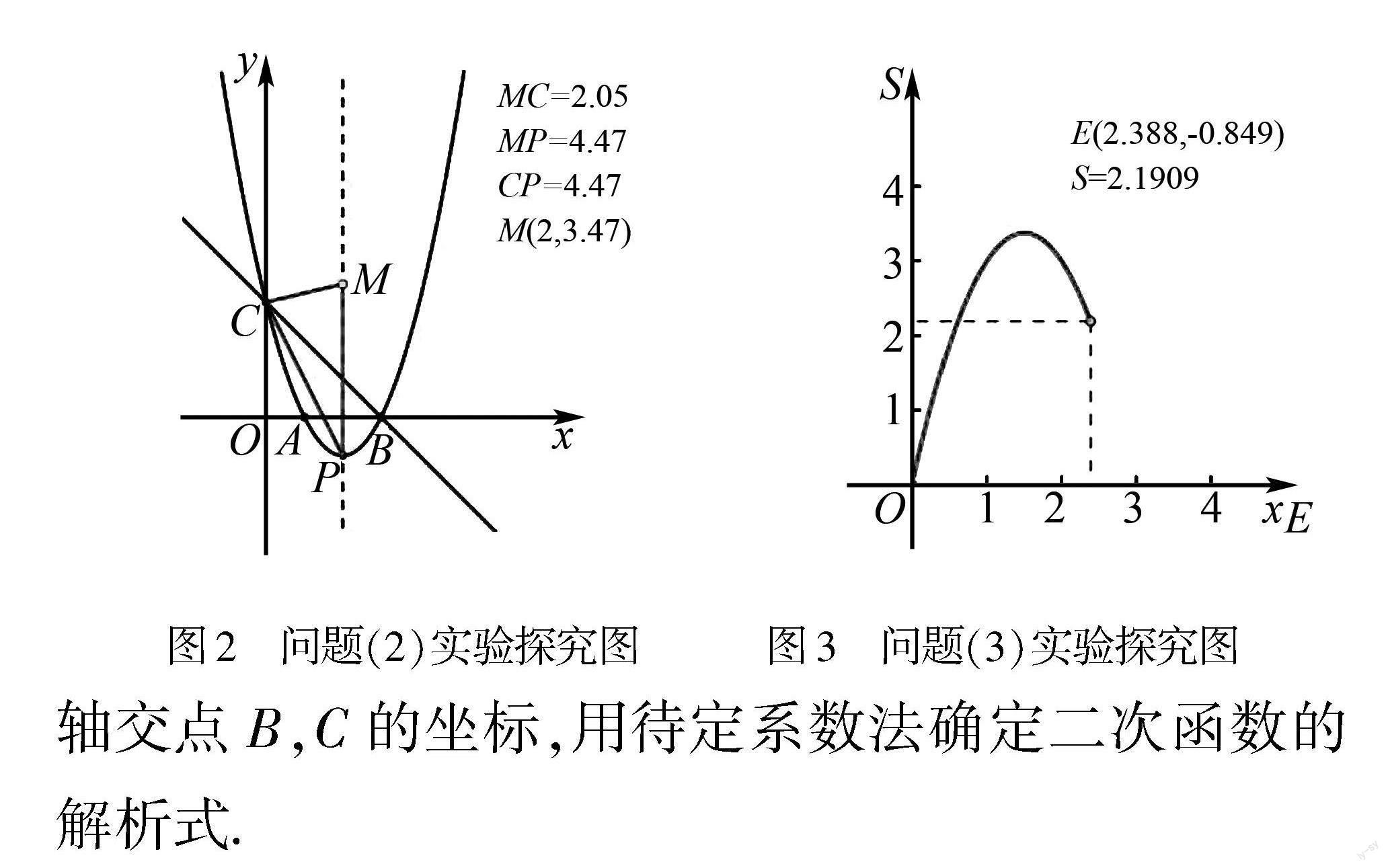
（3）當0

2 探究實驗

對于問題（2），如圖2所示，拖動點M，觀察△PCM三邊長度的變化，是否存在等腰三角形的情形？ 有幾種情況？

對于問題（3），如圖3所示，拖動點E，觀察△CBE的面積S和點E的橫坐標xE變化關系的圖象，猜測S是xE的什么函數.

3 思路分析

對于問題（1），求出直線y=-x+3與x軸、y軸交點B，C的坐標，用待定系數法確定二次函數的解析式.

對于問題（2），可用兩種不同方法求解.

方法1（幾何法）：由題意知，PC長度確定，PM，CM長度是變化的，并未說明PC是腰或底，因此需分MC=MP，CM=CP，PM=PC三種情況討論.動點M在對稱軸直線x=2上. 用“兩圓一線”法確定點M的位置，即作出線段PC的垂直平分線，或分別以點C，P為圓心，PC長為半徑作圓，與拋物線對稱軸交于點M1，M2，M3，M4，如圖4所示，所以滿足條件的點M只有4個，再結合條件求出點M的坐標.

方法2（代數法）：設M（2，m），根據勾股定理，可利用含m的代數式表示出三角形三邊的長，需分MC=MP，CM=CP，PM=PC三種情況列方程，可求得M點的坐標.

對于問題（3），過點E作x軸的垂線FE，交直線BC于點F，設點F（x，-x+3），Ex，x2-4x+3，用“寬高公式”表示出△CBE的面積，然后根據二次函數的性質即可求出面積的最大值.

4 解法探究

根據以上思路，可給出問題的具體求解過程.

（1）解? 因為直線y=-x+3與x軸、y軸分別交于點B，C，易知B（3，0），C（0，3）.從而易求得該拋物線的解析式為y=x2-4x+3.

（2）解法1? （幾何法）存在點M.因為y=x2-4x+3=（x-2）2-1，所以該拋物線對稱軸為直線x=2，頂點為P（2，-1）.

①如圖5，當MC=MP時，過PC中點D作直線l⊥PC于點D，交直線x=2于點M1，過點P作PE⊥y軸于點E，則PC=42+22=25，所以PD=5.因為M1P∥y軸，所以∠PCE=∠DPM1，所以

cos∠PCE=cos∠DPM1，即CEPC=PDPM1=425=5PM1，所以PM1=2.5，所以M12，1.5.

②如圖6所示，當PM=PC時，易求得M2（2，25-1），M3（2，-25-1）.

③如圖7所示，當MC=PC時，過點C作CF⊥PM4于點F，過點P作PE⊥y軸于點E，所以四邊形CEPF是矩形，則PF=CE=4，易求得M4（2，7）.

綜上可知，存在滿足條件的點M，其坐標為2，1.5或（2，7）或（2，-1+25）或（2，-1-25）.

解法2? （幾何法）存在點M.

①如圖8所示，作PC的垂直平分線交PC于點D，交拋物線的對稱軸于點M1，則CM1=PM1，所以△PCM1是等腰三角形，所以點M1為所求.過點D作y軸的平行線，過點C作x軸的平行線，兩直線相交于點E，過點M1作y軸的垂線交ED于點F.

因為P（2，-1），C（0，3），點D是PC的中點，所以D（1，1）.因為拋物線的對稱軸為直線x=2，所以CE=1，FM1=1，DE=2.易知△CED∽△DFM1.所以CEED=DFFM1，易知DF=0.5.從而可知M12，1.5.

②如圖9所示，以P為圓心，PC長為半徑作⊙P，交拋物線的對稱軸于點M2，M3，連接CM2，CM3，則PC=PM2=PM3，所以△PCM2，△PCM3都是等腰三角形.

過點M2作y軸的垂線，垂足為E，延長CP交⊙P于點D，過點D作x軸的垂線交EM2的延長線于點F，連接M2D.易知△ECM2∽△FM2D，所以ECEM2=FM2FD.易知m-32=2m+5，所以m=-25-1或m=25-1，所以點M2（2，25-1），M3（2，-25-1）.

③如圖10所示，以C為圓心，PC長為半徑作⊙C，交拋物線的對稱軸于點M4，連接CM4，則PC=CM4.延長PC交⊙C于點D，連接DM4，則△PCM4是等腰三角形.易知M4（2，7）.

綜上可知，存在滿足條件的點M，其坐標為2，1.5或（2，7）或（2，-1+25）或（2，-1-25）.

解法 3（代數法）： 因為y=x2-4x+3=（x-2）2-1，所以拋物線對稱軸為直線x=2，頂點為P（2，-1）.設M（2，m），又C（0，3），所以MC2=22+（m-3）2=m2-6m+13，MP2=（m+1）2，PC2=22+（-1-3）2=20，因為△CPM為等腰三角形，因此分三種情況討論：

①當MC=MP時，則有m2-6m+13=（m+1）2，解得m=1.5，此時M2，1.5；

②當MC=PC時，有m2-6m+13=20，解得m=-1（與P點重合，舍去） 或m=7，此時M（2，7）；

③當MP=PC時，則有（m+1）2=20，易得

M（2，-1+25）或（2，-1-25）.

綜上可知，存在滿足條件的點M，其坐標為2，1.5或（2，7）或（2，-1+25）或（2，-1-25）.

（3）當0

5 結束語

對于等腰三角形與拋物線相結合的存在性問題，可以把解題方法總結為“兩圓一線定位置，邊角相等分類列”.這里的“兩圓一線”法是已知等腰三角形一邊長度確定（這邊的端點至少有一個是定點），可以根據等腰三角形的性質作兩個輔助圓，或已知邊上的垂直平分線確定點的大致位置或解的個數，借助代數法求解，或利用定長線段所在直徑所對的圓周角是直角構造“一線三等角”相似模型的求解方法.

通過探究這類問題的求解方法，能有效提高學生分析問題和解決問題的能力.

參考文獻：［1］ 鄭利年，陳國玉.用角的關系，求動點的坐標［J］.中學數學研究（華南師范大學版），2023（14）：33-35.

［責任編輯：李? 璟］