基于數學抽象的高中數學教材分析與比較

趙健瀅 張怡文

摘要：數學抽象是高中階段的六個數學學科核心素養之一.本文中從數學抽象的視角對人教A版教材和蘇教版教材中“三角函數”一章的內容進行分析和比較，探尋教材落實發展學生數學抽象素養的要求以及兩版教材在這一方面的區別，以期為教師教學提供參考.

關鍵詞：數學抽象；人教A版；蘇教版；三角函數

1 研究問題

數學抽象主要包括從數量與數量關系、圖形與圖形關系中抽象出數學概念及概念之間的關系，從事物的具體背景中抽象出一般規律和結構，并用數學語言予以表征［1］.《普通高中數學課程標準（2017年版2020年修訂）》中將數學抽象置于六個核心素養之首，這表明了數學抽象素養的重要地位.

教材是教與學的重要材料.教師只有仔細研讀教材才能用好教材，充分發揮教材的價值.教材是如何將發展學生的數學抽象素養融入到教學內容之中？對此不同版本教材之間存在哪些區別？“獲得數學概念和規則，提出數學命題和模型，形成數學方法與思想，認識數學結構與體系”是數學抽象的四種表現［1］.這四種表現可視為數學學習中的四個過程，這些過程有賴于數學抽象的參與，因此有助于發展學生的數學抽象素養.“三角函數”一章內容豐富，是發展學生數學抽象素養的良好載體.為此，本文中選取高中數學人教A版教材（2019）和蘇教版教材（2020）（以下簡稱“人教A版教材”和“蘇教版教材”）中“三角函數”一章，以數學抽象的四種表現為分析維度嘗試回答上述兩個問題，以期為教師教學提供參考.

2 研究內容

2.1 獲得數學概念和規則

數學抽象的一個重要表現是獲得數學概念和規則.數學概念的獲得往往源于數學問題，而數學問題是抽象概念的源頭.具體到概念獲得的過程，有概念形成和概念同化兩種方式.概念形成模式包括“具體例子—觀察共性—抽象本質—形成定義—強化概念—概念應用”，概念同化模式包括“先行組織者—定義概念—強化概念—概念應用”［2］.“三角函數”一章中最重要的概念是三角函數的概念，對于三角函數概念的獲得，兩版教材都采用了概念形成的方式.此外，蘇教版教材還安排了對正弦、余弦、正切概念的學習，并用概念同化的方式獲得這三個概念.基于以上說明，下面按照獲得概念的順序從“提出問題”“抽象本質”“強化概念”三個方面對兩版教材中的相關內容展開分析.

（1）提出問題

三角函數在近代數學中的快速發展得益于其與圓周運動等周期現象的緊密聯系，兩版教材都注重向學生滲透這種聯系，提出用數學模型刻畫圓周上一點的運動情況，如表1所示.此外，蘇教版教材引導學生對這個問題進行初步分析后，將問題進一步明確為用模型刻畫兩種表示方法的關系.

（2）抽象本質

抽象本質是概念形成的重要環節.承接前面的問題，兩版教材中對三角函數概念本質的抽象過程如表2所示.蘇教版教材中，三角函數概念的建立需要借助任意角的正弦、余弦、正切概念.對于這三個概念的獲得，教材是在銳角的正弦、余弦、正切概念的基礎上直接給出定義.在這個過程中，蘇教版教材將初中和高中階段學習的正弦、余弦、正切的概念進行銜接，利于學生在舊知的基礎上學習新知.但是對學生而言，在經歷從銳角到任意角這一思維跨越時，他們是根據兩個定義之間形式上的相似而非本質上的相通來理解的.三角函數不以“代數運算”為媒介，是幾何量（角與有向線段）之間的直接對應，這是一個學習難點［3］.人教A版教材從角與坐標之間唯一確定的關系中抽象出正弦函數的概念，直接展示了正弦函數中幾何量之間的對應，利于突破這一難點.蘇教版教材從角與正弦值之間唯一確定的關系中抽象出正弦函數的概念，實際上正弦值是由坐標計算得來的，因此建立的也是幾何量之間的對應.但是學生在理解時，需要借助正弦值的概念才能“看到”這種對應，這可能會增加理解正弦函數對應關系的難度.

①當α為銳角時，由初中階段所學“銳角的正弦、余弦、正切”，有sin α=yr，cos α=xr，tan α=yx.一般地，將銳角推廣到任意角，在角終邊上任意取一點（異于原點），由形式上的相似給出任意角的正弦、余弦、正切的概念.

②當α=0，π6，π3，π2，……，11π6，2π時，計算sin α的值.把α的值看作橫坐標，對應的sin α的值看作縱坐標，在平面直角坐標系中描出點（α，sin α）.

③從以上計算過程和所畫的圖中可以得到：對于每一個實數α，都有唯一實數sin α與之對應，故sin α是α的函數.

（3）強化概念

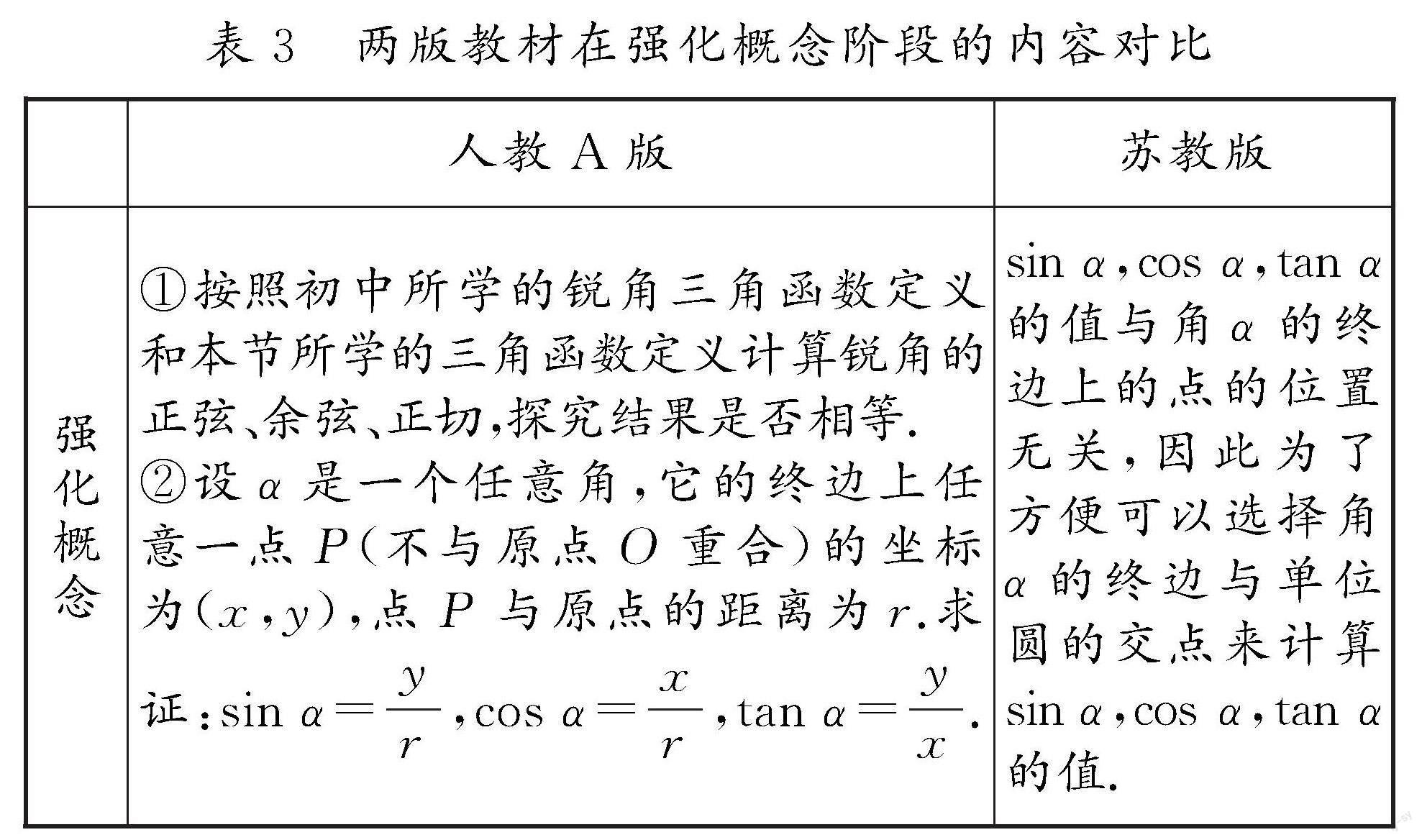
在強化概念環節中，學生將加深對概念的理解.選取人教A版教材對三角函數概念與蘇教版教材對正弦、余弦、正切概念的強化內容，具體見表3.下面圍繞其中的兩點區別進行分析.第一，關于對銳角三角函數與任意角的三角函數關系的處理，人教A版教材在得到任意角的三角函數后，再通過探究活動讓學生思考二者之間的關聯，進而認識到銳角三角函數與任意角的三角函數雖然來自不同的背景，但是存在聯系.蘇教版教材在銳角三角函數的基礎上得到任意角的三角函數，這樣的內容安排再現了歷史上由銳角三角函數再到任意角三角函數的發展歷程，但是學生可能會據此認為任意角的三角函數是由銳角三角函數推廣而來.第二，人教A版教材與蘇教版教材分別用“角終邊與單位圓交點的坐標”“角終邊上任意一點（異于原點）的坐標比”來定義三角函數，這是三角函數的兩種定義方式.在強化概念階段，兩版教材雖然沒有直接點明另外一種定義方式，但是對其有所滲透.人教A版教材引導學生通過證明認識到，由角α終邊上任意一點（不與原點O重合）的坐標都可求得角α的各個三角函數值.蘇教版教材在計算正弦、余弦、正切值的例題后指出：可以選擇角α的終邊與單位圓的交點計算角α的正弦、余弦、正切值.

2.2 提出數學命題和模型

（1）提出數學命題

“三角函數”一章中的數學命題主要有誘導公式.誘導公式的抽象過程是將圖形的對稱性用數學語言表達成三角函數的對稱性的過程.以公式sin（π+α）=－sin α為例，分析兩版教材中抽象出誘導公式的過程，其他誘導公式與此類似.

人教A版教材以“利用圓的對稱性研究三角函數的對稱性”導入.如圖1，任意角α的終邊與單位圓交于點P1，作P1關于原點的對稱點P2，以OP2為終邊的角記作β.如圖2，從點P1，P2的對稱關系出發，一方面得到角α，β終邊的對稱關系，進而得出兩角的關系為β=2kπ+（π+α）（k∈Z）.另一方面由單位圓的中心對稱性可知，點P2就在圓上，因此角α，β的終邊與單位圓的交點即為點P1，P2，進而利用這兩個點的對稱關系可以得到坐標的關系.由前者確定角的關系，由后者確定對應的正弦值的關系，兩相結合就得到誘導公式.

蘇教版教材以“終邊具有對稱關系的兩個角的三角函數值之間有什么關系”導入.已知角α的終邊與角β的終邊關于原點O對稱，且分別與單位圓交于點P，P′.如圖3，從角α，β終邊的對稱關系出發，由單位圓的中心對稱性得到交點P，P′的對稱關系，由此可得到它們坐標的關系，進而得到角α，β正弦值的關系為sin β=－sin α.最后將角β特殊化，因為角π+α與角α的終邊關于原點O對稱，所以用角π+α代替角β即得到誘導公式.

角α的終邊與角β的終邊關于原點對稱

單位圓的對稱性

角α，β的終邊與單位圓的交點P，P′關于原點對稱

點P，P′的坐標之間的關系

sin β=-sin α

角π+α與角α的終邊關于原點對稱

誘導公式

（2）提出數學模型

數學抽象的一個表現是“提出數學模型”，這也體現了數學抽象與數學建模兩種素養之間的聯系：通過數學抽象建立數學模型，在數學建模過程中發展數學抽象.“三角函數”一章主要涉及用函數y=Asin（ωx+φ）刻畫的勻速圓周運動模型和一般的周期運動模型.人教A版教材以“用數學模型刻畫勻速圓周運動”為問題，選取我國古代的筒車作為問題情境，用符號表示筒車運動過程中的若干物理量，分析這些量之間的關系，進而抽象出函數y=Asin（ωx+φ），回答了開始的問題.蘇教版教材由“確定時刻t時，摩天輪上一點P距離地面的高度”引入，通過分析與點P高度有關的物理量得到函數y=Asin（ωx+φ），再點明它的模型作用——描述勻速圓周運動.最后，兩版教材都以函數y=Asin（ωx+φ）為基礎，通過確定其中的參數建立了刻畫簡諧運動等一般周期運動的數學模型.

2.3 形成數學方法與思想

通過數學抽象可以挖掘出數學知識背后隱含的數學方法與思想，揭示知識的本質.除概念形成過程中從特殊到一般的思想，以及函數研究中常用的數形結合思想外，教材在三角函數這一章的內容設計還有助于學生形成以下數學方法與思想.兩版教材都從對稱的角度引入和推導誘導公式，另外人教A版教材從旋轉的角度推導兩角差的余弦公式，分別向學生滲透了對稱變換思想和旋轉變換思想.兩版教材中都只對誘導公式二給出了詳細的推導過程，公式三和公式四則仿照公式二的證明方式得到，在這個過程中學生可以領悟到類比推理思想.得到前四組誘導公式后，兩版教材都設置了求三角函數值的例題，引導學生發現利用這四組公式可以將任意角的三角函數轉化為區間0，π2內的角的三角函數.此外，人教A版教材在得到公式五和公式六后，指出利用它們實現正弦函數與余弦函數的相互轉化.這些都利于學生形成轉化與化歸思想.人教A版教材在研究正切函數時，采用了“周期性和奇偶性—圖象—其他性質”的方式.蘇教版教材在研究正弦函數、正切函數時，采用了“周期性—圖象—其他性質”的方式.兩版教材的內容雖然在具體安排上略有差別，但是正如蘇教版教材在“本章回顧”中指出的“依性作圖，以圖識性”，都能體現出圖象與性質之間的相互關系，強化圖象與性質之間“雙向研究”的方法.

2.4 認識數學結構與體系

認識數學結構與體系是數學抽象的一個較高水平的表現.三角函數是一類具體的函數，遵循函數研究的一般規律的“概念－性質－應用”，兩版教材的章節結構都體現了這一規律，這可以看成是這一章結構體系的“明線”.除此以外，兩版教材在內容中都設置了“暗線”.人教A版教材將單位圓作為暗線貫穿本章的主要內容，如圖4所示.蘇教版教材將三角函數線作為暗線貫穿三角函數值的幾何表示—誘導公式六—三角函數的圖象—三角函數的性質.

數學抽象素養內涵豐富，本文中以“三角函數”一章為例，從數學抽象的四種表現解讀了人教A版教材和蘇教版教材是如何發展學生數學抽象素養的，并揭示了兩版教材在這一方面各自的特點.實際教學中，教師應把握所用教材的特點，借鑒其中的先進理念，將發展學生的數學抽象素養真正地落實到課堂中.

參考文獻：

［1］中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）［S］.北京：人民教育出版社，2020：4-5.

［2］喻平.數學教學心理學［M］.2版.北京：北京師范大學出版社，2018：242-245.

［3］章建躍.用幾何直觀和代數運算的方法研究三角函數［J］.數學通報，2020，59（11）：4-13，57.