基于SSA-BGOMP的滾動軸承振動信號壓縮重構方法

羅國慶，胡東，趙仲勇a，廖潤，謝菊芳

（1.西南大學 a.工程技術學院；b.智能電網及裝備新技術國際研發中心，重慶 400715；2.中國南方工業集團軍品部，北京 100089）

近年來，隨著工業化的發展，傳感器在大型機械設備上的檢測與采樣愈發復雜，依據傳統奈奎斯特采樣定理進行采樣得到的數據量巨大，數據的實時采集、存儲困難，而且會引發傳感器功耗激增、續航過短等問題。壓縮感知理論提出稀疏信號可以用遠低于奈奎斯特采樣定理要求的采樣頻率進行采樣［1］，為處理海量數據提供了新的思路，因此被廣泛應用于壓縮成像［2］、語音信號處理［3］、雷達探測［4］等領域。

壓縮感知要求信號本身稀疏或在某個變換域上稀疏。最常見的變換域是正交基完備稀疏字典，但其靈活性較差，處理具備復雜特性的軸承振動信號時稀疏性較差，信號重構效果不佳［5］。基于字典學習算法的字典可以更好地適應軸承振動信號自身的特性，K?奇異值分解（K?Singular Value Decomposition，K?SVD）算法在最優向量法［6］的基礎上優化了順序更新列［7］，其生成的過完備字典與原信號的匹配度高，稀疏效果好［8］。文獻［9?10］在不同振動信號的壓縮感知過程中利用K?SVD 訓練過完備字典稀疏信號，有效提升了振動信號的壓縮感知性能。然而，常見的重構算法在K?SVD 過完備字典上恢復振動信號的應用效果并不理想［11］，重構效果仍有待提升。

傳統的信號重構算法有以正交匹配追蹤算法（Orthogonal Matching Pursuit，OMP）［12］為代表的貪婪算法和以基追蹤算法（Basis Pursuit，BP）［13］為代表的凸優化算法。貪婪算法的重構效率高，但易陷入局部最優；凸優化算法的精度高，但計算復雜度過高，不符合實際應用要求。廣義正交匹配追蹤算法（Generalized Orthogonal Matching Pursuit，GOMP）［14］在OMP 基礎上改變了原子選擇方式，通過每次選擇多個原子加快了收斂速度，但其無法剔除每次迭代中的錯誤原子，重構精度不佳。文獻［15］在GOMP 迭代后對系數施加約束，提出了基于約束的廣義正交匹配追蹤算法，抗噪性有所提升，但仍無法在迭代中剔除錯誤原子。文獻［16］引用子空間追蹤（Subspace Pursuit，SP）思想提出了基于子空間的廣義正交匹配追蹤算法，其在糾正原子時選擇絕對值最大的k項作為原始信號最終估計值，而實際應用中的信號相對k是稀疏的，因此該算法在實際應用中的重構誤差較大，細節信息丟失嚴重［17?18］。

針對上述問題，本文提出基于麻雀搜索算法?回溯廣義正交匹配追蹤（Sparrow Search Algo?rithm ?Back GOMP，SSA?BGOMP）的軸承振動信號壓縮感知方法，利用高斯隨機矩陣對軸承振動信號進行壓縮采樣，利用K?SVD 訓練樣本信號得到稀疏字典，在GOMP 基礎上引入改進的回溯機制，通過SSA［19］自適應設置閾值的方式對支撐集原子進行二次回溯篩選，降低錯誤原子與噪聲分量被選入支撐集的概率，提升算法的抗噪性以及重構效果。

1 壓縮感知與降噪

壓縮感知理論提出，當信號稀疏或其在某個變換域上稀疏，就可以用一個與變換基不相關的觀測矩陣將高維信號投影到一個低維空間上，得到一個遠小于信號長度的觀測值，通過優化求解就能夠從相對少的投影中構造出一個近似原信號的重構信號。

設f為有限實值離散空間，壓縮感知要求f的信號是稀疏的，其數學模型為

式中：f為原始信號；Ψ為正交基矩陣，Ψ=(φ1，φ2，…，φN)；α為原始信號f在正交基矩陣Ψ上的稀疏投影。設α有k(k＜＜n)個非零系數。k為稀疏度，是衡量原始信號f在Ψ上稀疏效果的指標。

獨立同分布的高斯隨機變量形成的觀測矩陣與任意正交基矩陣Ψ具有較強的不相關性［20］，而且高斯隨機矩陣與Ψ形成的感知矩陣滿足有限等條件（Restricted Isometry Property，RIP）且約束等距常數δk較小［21］，則觀測值y可表示為

聯立（1），（2）式可得

式中：Φ為觀測矩陣；Θ為感知矩陣。

上述問題轉換為從觀測值y中恢復原始信號f，需從觀測值y中求解稀疏投影α，即求解如下的最優化問題

最小L0范數可在一定條件下轉換為最小L1范數以找到最稀疏的解，則（4）式可轉換為

設原始信號f由純凈信號x與噪聲信號n構成，即f=x+n，將其在正交基矩陣Ψ展開可得

與（3）式聯立可得

式中：αx，αn分別為x和n在Ψ上的稀疏投影。設αx，αn的稀疏度分別為kx和kn，由于n不具備稀疏性，而x可以被正交基矩陣Ψ稀疏，則有kn＜＜kx。因此，可以從原始信號f中較好的重構出純凈信號x，噪聲信號n則很難重構，即壓縮感知可以在重構過程中過濾噪聲。

2 SSA?BGOMP

當α是稀疏度為k的稀疏投影時，其內部會存在大量的0 元素。感知矩陣Θ中對應α為0 位置的列不會影響壓縮感知重構，只有α非0位置的列才會影響壓縮感知重構。對于感知矩陣Θ，將對應α為0 位置的列合并為無效支撐集I，對應α非0位置的列合并為有效支撐集E，即

則由壓縮感知理論可得

壓縮感知的支撐集原子選擇過程就是尋找有效支撐集E中全部原子的過程。GOMP 算法每次選擇S個原子（默認值為k/4），雖然增加了選入有效支撐集原子的概率，但也增加了選入無效支撐集原子的概率，而且無法剔除無效支撐集原子。因此，本文在GOMP 算法中引入回溯思想降低錯誤原子選入支撐集的可能性。在迭代過程中，通過SSA 自動設置閾值過濾無效支撐集原子，降低錯誤原子被選入支撐集的概率，從而更好地重構原始信號的細節信息，并提升壓縮感知重構效果及其降噪能力。SSA?BGOMP 算法流程如圖1 所示，算法具體描述如下。

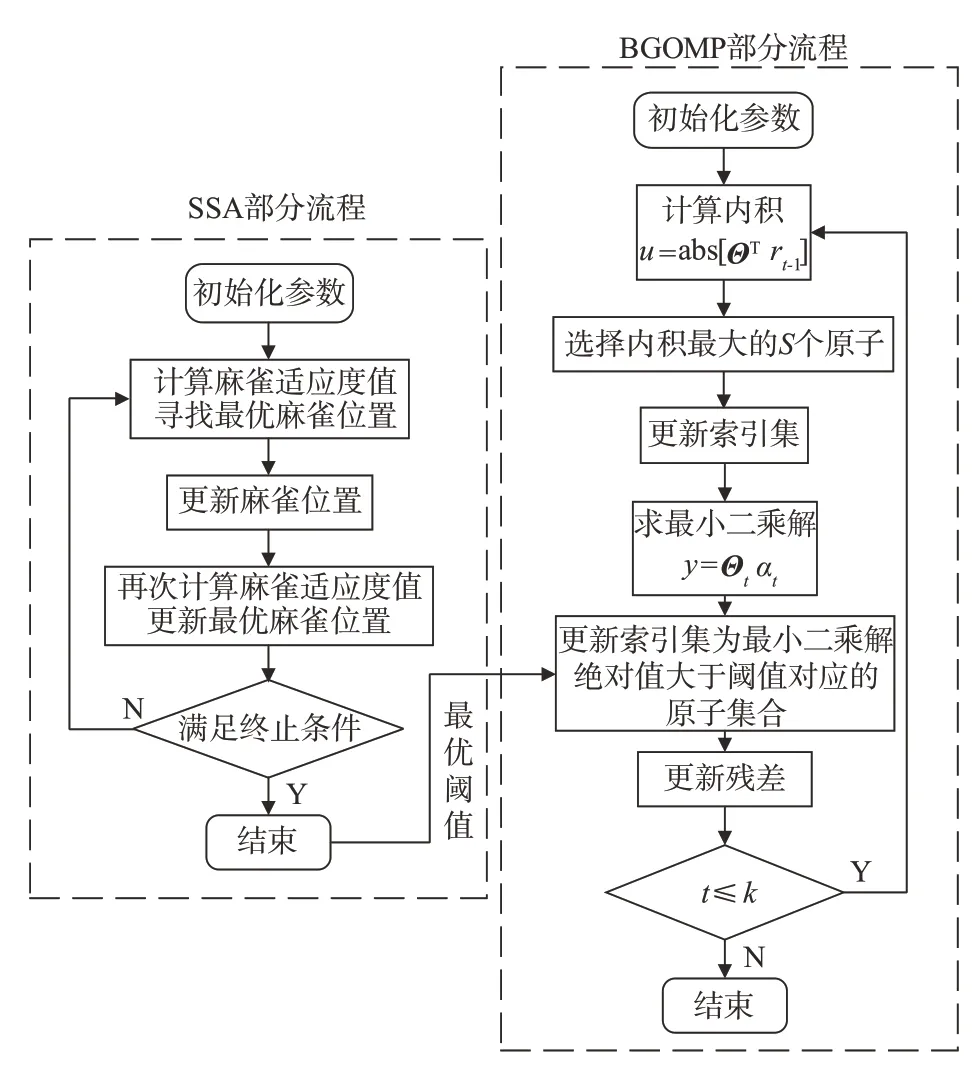
圖1 SSA?BGOMP算法流程圖Fig.1 Flow chart of SSA?BGOMP algorithm

輸入：觀測值y；感知矩陣Θ=ΦΨ；稀疏度k；每次選擇原子的個數S，默認值k/4，若k＜4 則取N= 1；

初始化：r0=y，Λ0= ?，t= 1；設定SSA 的參數，當滿足終止條件后得到最優閾值μ；

Fort= 1：k

（a）更新索引集：求u= abs[ΘTrt?1]，取值最大的S個并將其對應ΘT中的列序號j構成一個列序號集合J0；令Λt=Λt?1∪J0，Θt=Θt?1∪θj(for allj∈J0)；

（b）求最小二乘解：求y=Θtαt的最小二乘解α?t；

（c）篩選索引集原子：更新Λt為最小二乘解絕對值大于閾值μ對應的原子集合；

（d）更新殘差：rt=y?

End

3 仿真分析

為驗證SSA?BGOMP 算法重構信號的效果，選用長度為256 的高斯隨機信號作為仿真信號，與OMP，壓縮采樣匹配追蹤（Compressive Sampling Matching Pursuit，CSMP），SP，GOMP，SSA?BGOMP 算法進行對比分析。仿真信號的稀疏度k以5為步長從5增至50，觀測矩陣為100×256的高斯隨機矩陣，壓縮率為60%；SSA?BGOMP與GOMP每次選擇的原子數取默認值，SSA的參數設置見表1。相對誤差小于0.1%時記為重構成功，試驗重復運行100次并記錄成功次數，成功重構率及其相對誤差如圖2所示：SSA?BGOMP算法重構信號的成功率隨稀疏度的增加下降的最慢，在k為35時成功率仍大于70%，遠高于其他算法，而且其重構信號的相對誤差最小，重構信號比其他算法更接近原始信號。

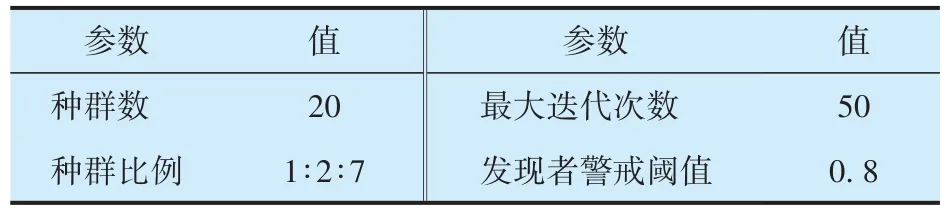
表1 SSA參數設置Tab.1 Parameter settings of SSA

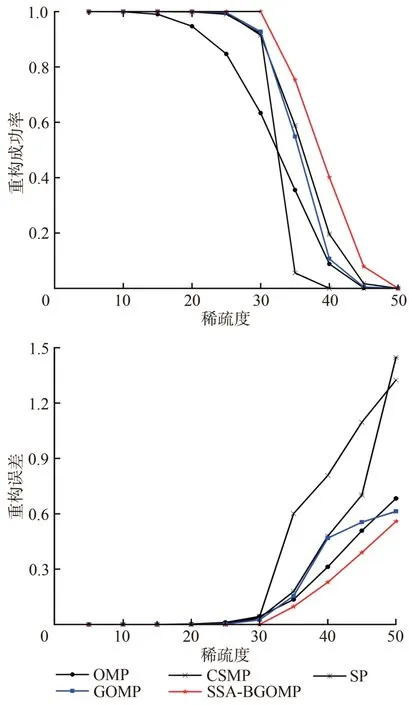
圖2 不同算法重構信號的成功率及其相對誤差Fig.2 Successful rates and relative errors of reconstructed signals by different algorithms

向仿真信號中加入信噪比30 dB 的高斯白噪聲，在其他條件不變的工況下對比不同算法的峰值信噪比（Peak Signal To Noise Ratio，PSNR），試驗重復運行100 次以驗證SSA?BGOMP 算法的抗噪性，結果如圖3所示；另外，將仿真信號的稀疏度k設為25，在其他條件不變的工況下對比不同算法的運行時間，試驗重復運行10 次以驗證SSA?BGOMP算法的計算效率，結果如圖4所示。由圖3、圖4可知：SSA?BGOMP 算法重構信號的峰值信噪比最高，重構信號所需時間也低于OMP，CSMP 和SP 算法，抗噪性良好的同時在計算效率上也具備一定優勢。

圖3 不同算法重構信號的信噪比Fig.3 SNR of reconstructed signals by different algorithms

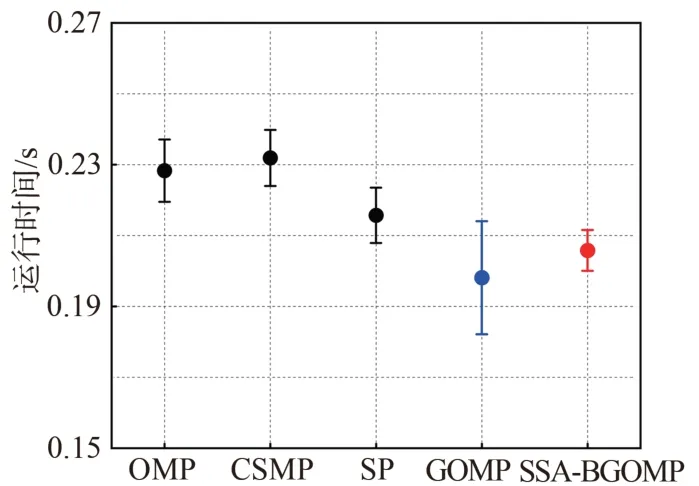
圖4 不同算法重構信號所需時間Fig.4 Time required for reconstructed signals by different algorithms

仿真分析表明，引入回溯思想后，SSA?BGOMP 算法不僅保留了GOMP 算法運行時間低的優勢，而且重構效果明顯提升，其綜合重構性能優于其他算法。

4 試驗驗證

4.1 試驗數據

選用凱斯西儲大學（CWRU）以及西安交通大學（XJTU?SY）軸承數據集進行試驗。CWRU 數據集包含驅動端軸承的正常信號以及鋼球、外圈、內圈故障信號，XJTU?SY 數據集則包含外圈、內圈故障信號。其中，N 表示正常信號，B，OR，IR 分別表示鋼球、外圈、內圈故障信號。信號采樣點數取1024，CWRU 數據集中4 種原始信號的時域波形如圖5所示。

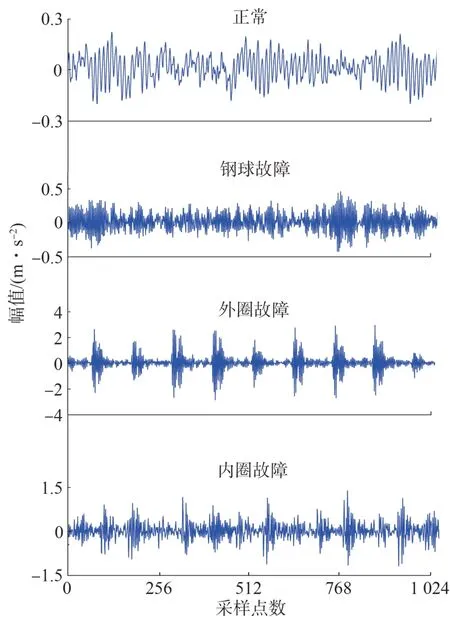
圖5 CWRU數據集的4種原始信號Fig.5 Four initial signals in CWRU dataset

4.2 評價指標

使用相對誤差σ以及峰值信噪比PPSNR共同衡量軸承振動信號壓縮重構效果，其定義為

式中：σ為相對誤差；f為原始信號；為恢復信號；EMES為均方根誤差。σ越小，說明壓縮感知效果越好；PPSNR越大，說明壓縮感知降噪效果越好。

另外，使用壓縮率r表示軸承振動信號的壓縮程度，即

式中：n為原始信號的長度；m為觀測值的長度。壓縮率越大，說明信號的壓縮程度越高。

4.3 信號重構

為驗證SSA?BGOMP 算法對實際信號的重構效果，分別選擇OMP，CSMP，SP，GOMP，SSA?BGOMP 算法對軸承振動信號在DCT 完備字典上進行壓縮率為0.5 ～ 0.7 的壓縮感知重構，每組試驗重復100次取平均值，記錄相對誤差以及峰值信噪比，結果見表2：信號類別、壓縮比共同影響信號的壓縮重構效果，當壓縮觀測條件相同時，SSA?BGOMP 算法在CWRU 與XJTU?SY 軸承數據集中均取得了比其他貪婪算法更低的相對誤差以及更高的峰值信噪比。其中，SSA?BGOMP 比GOMP 的相對誤差降低2% ～ 12%，比SP算法的相對誤差降低3% ～ 9%。

4.4 對比試驗

為驗證本文方法對實際信號的重構效果，對CWRU 軸承振動信號分別選擇OMP，CSMP，SP，GOMP，SSA?BGOMP 共5 種貪婪算法，在圖5 信號訓練的K?SVD 字典上，進行壓縮率為0.5 ～ 0.7的壓縮感知重構，并記錄相對誤差以及峰值信噪比。

K?SVD 算法生成過完備字典的參數依據文獻［5］選擇，字典長度為1024×1920，稀疏表示時最多線性組合原子數為10，訓練迭代次數為10，選用樣本信號自身原子進行訓練。每組試驗重復100次取平均值，不同重構算法對CWRU軸承振動信號在K?SVD 字典上的相對誤差和峰值信噪比見表3：在K?SVD 字典上重構軸承振動信號時，SSA?BGOMP 的重構相對誤差依然最低，效果最穩定，比GOMP 的相對誤差降低3% ～ 13%，比SP 的相對誤差降低5% ～ 20%，說明其更適用于軸承振動信號的壓縮感知重構。

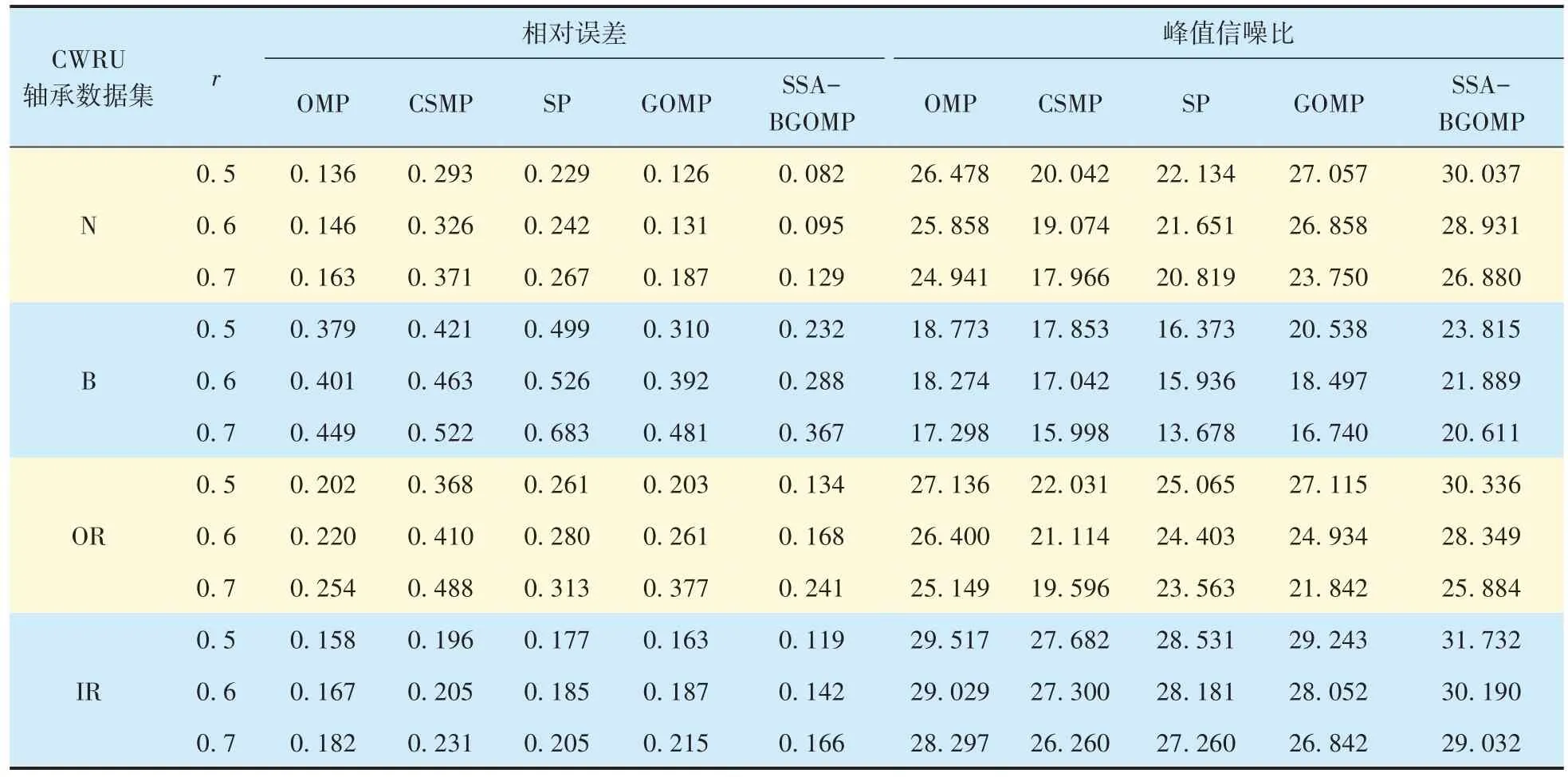
表3 K?SVD過完備字典上各重構算法在不同壓縮率下的相對誤差和峰值信噪比Tab.3 Relative errors and PSNR of different reconstruction algorithms on K?SVD overcomplete dictionary under different compression rates

對比表2、表3 可知：K?SVD 過完備字典對CWRU 滾動軸承振動信號壓縮重構效果提升顯著，正常與內、外圈故障信號在K?SVD 過完備字典上的重構效果較好，鋼球故障信號的稀疏表示效果欠佳，在壓縮率過高時相對誤差較大。壓縮感知過程中，壓縮率越大，壓縮觀測后的數據量越少，但壓縮率過高會導致數據丟失，因此在進行壓縮觀測時壓縮率不易過高。

在壓縮率為0.6的情況下，應用本文方法對圖5所示軸承振動信號進行重構，重構信號的時頻域波形如圖6 所示：正常和內、外圈故障信號在壓縮重構后仍保留了原始信號的全部信息；鋼球故障信號壓縮重構后在時域上有輕微偏差，但頻域分布趨勢基本一致，關鍵信息得到了保留；結果表明，軸承振動信號經本文方法壓縮重構后可以保持原有趨勢不變，而且能保留關鍵特征信息，可用于后續的數據分析。

圖6 CWRU軸承數據集原始信號重構后的時頻域波形Fig.6 Time?frequency domain waveform reconstructed from original signals of CWRU bearing dataset

4.5 本文方法對故障特征提取的影響

為進一步驗證本文方法壓縮重構后的振動信號能否用于后續數據分析，以CWRU 軸承數據集的軸承外圈故障信號為例進行分析，采樣頻率為12 kHz，數據長度為12000，計算可得外圈故障特征頻率為107.4 Hz。

外圈故障原始信號及其希爾伯特包絡譜如圖7 所示，可以清晰觀察到109 Hz 的外圈故障特征頻率及其倍頻。

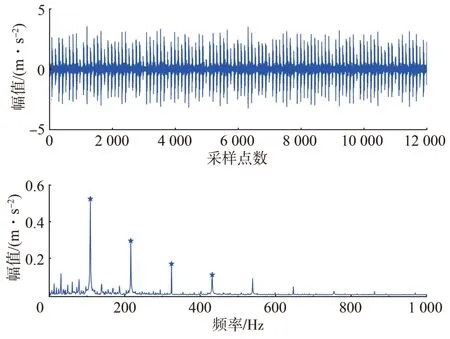
圖7 外圈故障原始信號特征分析Fig.7 Analysis on original signal characteristics of outer ring fault

為驗證重構后的恢復信號能否保留原信號特征，在壓縮率為0.8的情況下，應用本文方法對外圈故障原始信號進行壓縮重構。重構信號及其希爾伯特包絡譜如圖8所示，重構信號僅幅值發生輕微偏差，仍可清晰分辨外圈故障特征頻率及其倍頻。

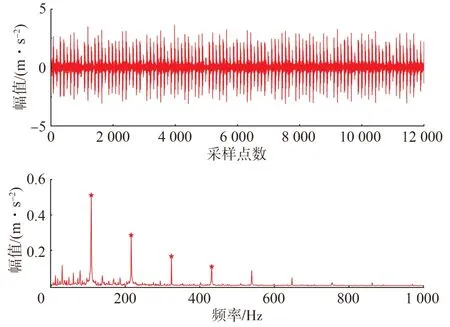
圖8 外圈故障重構信號特征分析Fig.8 Analysis on reconstructed signal characteristics of outer ring fault

5 結束語

為改善軸承振動信號的壓縮感知效果，針對GOMP 算法在迭代過程中無法剔除錯誤原子的問題，提出了基于SSA?BGOMP的滾動軸承振動信號壓縮感知方法。該方法具有一定的自適應性，在提升壓縮感知恢復效果的同時并未添加新的人工選擇參數，可以有效緩解數據量過多為數據處理帶來的壓力。仿真與試驗分析表明，本文方法對比其他貪婪算法具有明顯優勢，可以有效改善軸承振動信號的壓縮感知效果。經過本文方法壓縮重構后的恢復信號，數據特征參量能夠被完整保存，可應用于后續數據處理。