邊坡在不同坡度下的穩定性研究

◇聊城大學建筑工程學院 段兆岢 劉 瑞 殷志偉 侯奉展 王仕豪

由于降雨入滲、地震破壞以及地質構造變化等因素，往往造成邊坡巖土體在自身重力的作用下沿滑動面整體下滑，出現失穩坍塌、滑坡等現象。并且邊坡失穩造成的地質災害嚴重危害工程建設和人民生命財產安全，所以必須加強對邊坡穩定性的研究分析。本文基于Midas-GTS/NX有限元軟件建立三維模型，通過改變邊坡坡度，對邊坡在自然狀態與降雨工況下的穩定性進行模擬分析。隨著邊坡坡度的增大，其模擬結果顯示：自然狀態下邊坡沿X軸方向的位移量變大；降雨工況下邊坡孔隙水壓力增大，土體抗剪強度降低；邊坡坡度越大，邊坡的安全系數越小，邊坡越不穩定。同時，三種邊坡在降雨工況下的安全系數均低于自然工況下的安全系數。通過對不同工況下的邊坡穩定性進行數值模擬，根據位移量、剪應力、應變、孔隙水壓力、安全系數等對邊坡進行穩定性分析，旨在對其他關于邊坡的穩定性研究提供參考。

隨著我國經濟實力的日益增長，人們對美好生活的需要也越來越強烈，這加速著建設工程的發展，類似于公路、鐵路等大量基礎設施開始在全國范圍內建設。基礎設施建設工程中，路基邊坡、填筑邊坡等邊坡數量也在快速增長，但與此同時邊坡滑坡、崩塌等現象經常發生，嚴重危害著人們的生產生活和生命安全。據統計我國平均每年發生滑坡和泥石流地質災害2萬余起、傷亡1千余人、受災人口90多萬，直接經濟損失20-60億元[1]，所以在邊坡工程中，邊坡的安全問題尤為重要。造成邊坡滑坡、崩塌的因素包括內部因素和外部因素兩大類，其中邊坡坡度和降雨入滲對邊坡穩定性有著一定的影響。

目前在建模時一般選用四類典型邊坡：均質邊坡、填方邊坡、二元結構邊坡、含軟弱夾層邊坡進行分析。本文選用二元結構邊坡，二元結構邊坡是比較常見的結構形式，即在山地表層為上覆松散堆積土層，下部為堅硬的基巖，控制性結構面是土巖層的交界面[2]。本文基于Midas-GTS/NX有限元軟件通過對30°邊坡、45°邊坡、60°邊坡在自然、降雨兩種不同工況下進行穩定性分析。

1 計算方法及有限元模型的相關參數

1.1 強度折減法（SRM）

在使用Midas-GTS/NX有限元軟件進行邊坡穩定性分析時，巖土層本構模型采用摩爾-庫侖本構模型，并運用基于有限單元法的強度折減法（SRM）進行分析。強度折減法（SRM）是土層黏聚力C同折減系數F的比值，土體內摩擦角同安全系數的比值[3]。在迭代計算過程中，抗剪強度的參數C值和值不斷減小，最終計算至邊坡達到失穩破壞狀態，此刻的折減系數F值便成為邊坡穩定的安全系數。迭代計算方程如下：

1.2 模型尺寸

在本文的數值模擬模型建立中，設置了30°、45°、60°三種邊坡角度，三種坡度的邊坡高度均為30m，坡體寬度均為12m，其中坡度為30°邊坡的坡體長64.64m，坡度為45°邊坡的坡體長50m，坡度為60°邊坡的坡體長41.5m，如圖1所示。

圖2 X軸方向位移云圖

圖3 最大剪應力云圖

圖4 塑性應變云圖

圖5 X軸方向位移云圖

圖6 最大剪應力云圖

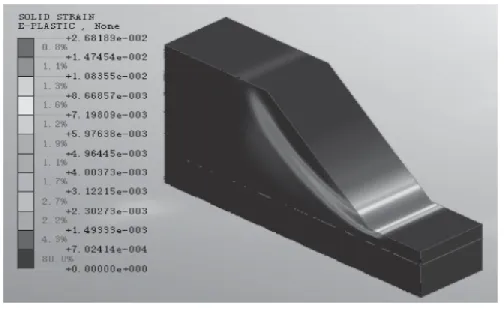
圖7 塑性應變云圖

圖8 X軸方向位移云圖

圖9 最大剪應力云圖

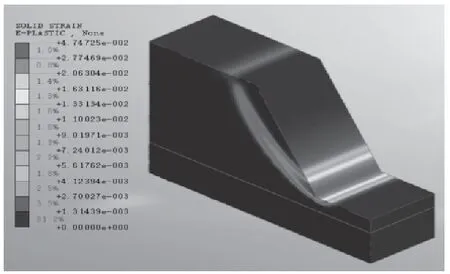
圖10 塑性應變云圖

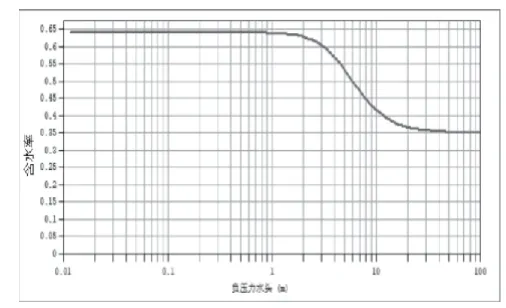
圖11 水土特征曲線

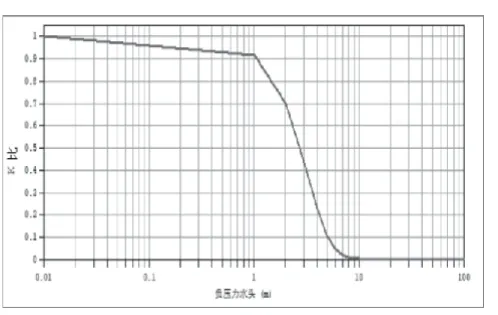
圖12 滲透曲線

圖13 30°邊坡孔隙水壓力云圖

圖14 45°邊坡孔隙水壓力云圖

圖15 60°邊坡孔隙水壓力云圖

1.3 巖土體基本參數

運用Midas-GTS/NX有限元軟件進行邊坡模型建立時，需要考慮巖土體的物理力學參數。根據工程地質勘察數據以及實地取樣進行室內三軸等試驗[4]，得出巖土體的容重γ、粘聚力、摩擦角、泊松比、彈性模量E等參數（表1）。由此保證模型的各巖土層盡量符合實際工程地質，同時保證邊坡穩定性分析數據的準確性以及真實性。

表1 巖土體基本參數

2 自然工況下邊坡穩定性分析

2.1 邊坡計算模型

劃分網格時，根據邊坡巖土體物理力學參數表添加土層材料，建立土層材料屬性，并選擇摩爾-庫倫本構模型。在邊坡分析施加荷載、邊界條件時，選擇軟件邊界屬性中的自動約束功能，對自然狀態下不同坡度的邊坡施加邊界約束，同時荷載僅選擇自身重力。最后，通過選擇分析工況中邊坡穩定（SRM）這一求解類型來進行模擬計算，求得自然工況下的邊坡安全系數。經查GB50330-2013《建筑邊坡工程技術規范》[5]知邊坡穩定狀態劃分標準，見表2。

表2 邊坡穩定狀態劃分標準表

2.2 30°邊坡模型結果分析

如圖所示，自然狀態下30°邊坡在邊界約束與自身重力加載作用下，邊坡沿X軸方向的位移大部分出現在邊坡坡面上，并且最大位移量為0.051m，而邊坡內部的位移量相對較小。同時由最大剪應力云圖可見，30°邊坡未出現應力集中區。根據塑性應變云圖可以看出塑性區的最大值為0.022m，發生坡災害的潛在危險低。模擬計算結果顯示30°邊坡的安全系Fs=1.724，結合邊坡穩定狀態劃分標準（表2）可判斷，30°邊坡處于穩定狀態。

2.3 45°邊坡模型結果分析

由沿X軸方向的位移云圖可見，45°的邊坡的位移量也集中在邊坡坡面上，隨著邊坡角度的增大，坡面上部位移量減小，同時其最大位移量出現在高12.3m處，最大位移量為0.064m。通過最大剪應力云圖、塑性應變云圖發現，45°邊坡未出現剪應力集中區，并且45°邊坡塑性區最大值位于坡腳處，最大值為0.027m。數值模擬結果顯示45°邊坡的安全系數=1.241≥1.15，所以45°邊坡處于穩定狀態。

2.4 60°邊坡模型結果分析

由圖可知60°邊坡沿X軸方向最大位移量為0.109m，未出現剪應力集中區，60°邊坡的塑性區最大值達到0.047m。數值模擬結果顯示60°邊坡的安全系數=0.965＜1.00，所以根據邊坡穩定狀態劃分標準（表2）判斷，60°邊坡處于不穩定狀態。

3 降雨工況下邊坡穩定性分析

3.1 降雨工況設計

本文降雨工況設計選擇的降雨強度為特大暴雨，降雨量為300mm/d，持續時間為10小時。并且在模型左側施加17m的初始左側水頭，右側施加5m的初始右側水頭。

3.2 土壤持水曲線

滲透性函數和含水率函數選擇的函數類型為vanGenuchten，該土壤持水曲線vanGenuchten模型的表達式[6]為：

3.3 模型結果分析

在降雨過程中，由于雨水入滲角和地表徑流的存在，邊坡坡度會對雨水的入滲量產生直接影響[7]。在保持相同的降雨強度、時間的條件下，通過改變邊坡角度，對比分析30°、45°、60°邊坡的孔隙水壓力以及其安全系數，總結降雨前后的邊坡穩定性變化。

（1）孔隙水壓力分析。

截取三種邊坡降雨時間0h、5h的邊坡孔隙水壓力云圖，通過觀察發現：隨著雨水不斷滲入巖土體，和降雨0h的邊坡孔隙水壓力云圖相比，降雨5h時邊坡頂部的孔隙水壓力值有明顯的增大，邊坡坡腳處的孔隙水壓力等值線略有彎曲，但坡底后緣處孔隙水壓力變化不大。同時模型的模擬結果顯示，降雨10h時30°、45°、60°邊坡的最大孔隙水壓力分別為182.7kPa、166.9kPa、154kPa，隨著邊坡角度的增大，邊坡的孔隙水壓力值變小。

（2）安全系數分析。

如圖16所示，降雨10h后的三種坡度邊坡的安全系數分別為1.542、1.051、0.824。當邊坡坡度越大時，邊坡安全系數越小，從而邊坡的穩定性越差。在30°～45°范圍內，邊坡安全系數變化比率較大，由此說明在該坡度范圍內，雨水入滲速度較快，影響邊坡穩定性程度大。

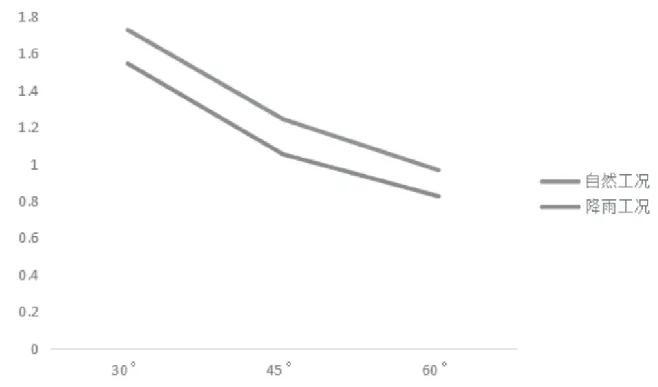
圖16 不同角度邊坡降雨前后安全系數

4 結論

本文通過Midas-GTS/NX軟件的數值模擬，結合相關巖土體物理力學參數建立邊坡三維模型，對三種不同角度的邊坡進行對比分析，以下是得到的結論。

（1）在自然工況條件下，邊坡坡度越大，其X方向的位移量越大，邊坡安全系數越小。

（2）在降雨工況條件下，邊坡坡度越大，坡面雨水在地表徑流的流速越快，同時雨水入滲量也增大。在雨水入滲后，坡頂的基質吸力開始下降，土體內孔隙水壓力增大，使得邊坡土體抗剪強度降低，邊坡更容易失穩。

（3）在兩種工況下，三種坡度邊坡的安全系數皆隨坡度的增大而減小。同時降雨工況下三種坡度邊坡的安全系數均低于自然工況下的安全系數。