Cahn-Hilliard方程的一個超緊致有限差分格式

栗雪娟，王丹

(西安建筑科技大學 理學院，陜西 西安 710055)

本文考慮的四階Cahn-Hilliard方程為

(1)

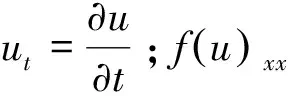
1958年,Cahn和Hilliard提出Cahn-Hilliard方程,該方程最早被用來描述在溫度降低時兩種均勻的混合物所發生的相分離現象。隨著學者對該方程的研究越來越深入,該方程的應用也越來越廣泛,特別是在材料科學和物理學等領域中有廣泛的應用[1-3]。

Cahn-Hilliard方程的數值解法目前已有很多研究,文獻[4]使用了全離散有限元方法,文獻[5]使用了一類二階穩定的Crank-Nicolson/Adams-Bashforth離散化的一致性有限元逼近方法,文獻[6-7]使用了有限元方法,文獻[8]使用了不連續伽遼金有限元方法,文獻[9]使用了Cahn-Hilliard方程的完全離散譜格式,文獻[10]使用了高階超緊致有限差分方法,文獻[11]使用了高階優化組合型緊致有限差分方法。

綜上所述,本文擬對Cahn-Hilliard方程構造一種新的超緊致差分格式,將空間組合型超緊致差分方法和修正的時間四階Runge-Kutta方法相結合,求解Cahn-Hilliard方程的數值解,得到相對于現有廣義格式精度更高的數值求解格式,并對組合型超緊致差分格式進行誤差估計,最后通過數值算例驗證該方法的可行性。

1 高階精度數值求解方法

1.1 空間組合型超緊致差分格式

早期的緊致差分格式是在Hermite多項式的基礎上構造而來的,Hermite多項式中連續三個節點的一階導數、二階導數和函數值的數值關系可以表示為

(2)

1998年,Krishnan提出如下緊致差分格式:

(3)

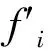
式(2)對應f(x)展開以xi為鄰域的泰勒級數為

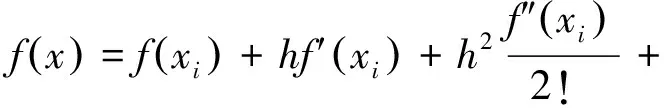
(4)

差分格式的各項系數由式(3)決定,可得到如下的三點六階超緊致差分格式:

(5)

為優化三點六階緊致差分格式,并保持較好的數值頻散,將迎風機制[12]引入式(5),構造出如下三點五階迎風型超緊致差分格式:

(6)

左右邊界可達到三階精度緊致格式:

(7)

(8)

上述組合型超緊致差分格式只需要相鄰的三個節點便可以同時求得一階導數和二階導數的五階精度近似值,比普通差分格式的節點更少,降低了計算量。

為便于編程計算,將上述構造的組合型超緊致差分格式重寫為矩陣表達形式。假設U為位移矩陣,其大小為m×n,則求一階導數和二階導數的離散過程可以用矩陣運算表示為

AF=BU,

(9)

結合內點的三點五階迎風型超緊致差分格式和邊界點的三點三階差分格式,組成式(9)中等式左邊的矩陣A和等式右邊的矩陣B,大小分別為2m×2n和2m×n;F為奇數行為空間一階導數和偶數行為空間二階導數組成的矩陣,大小為2m×n。以上矩陣分別為:

(10)

(11)

(12)

(13)

由式(9)可得

F=A-1BU。

(14)

解線性代數方程組(9)可得Cahn-Hilliard方程的空間一階導數和二階導數。對于四階導數,可將已求得的二階導數替代式(14)中的U,再次使用式(14)進行求取。

1.2 時間離散格式

在對很多偏微分方程的數值求解中不僅需要高精度的空間離散格式,同時還需要高精度的時間離散格式。普通的一階精度時間離散格式顯然滿足不了高精度計算要求,因此本文選用時間四階Runge-Kutta格式進行時間離散。Runge-Kutta方法是基于歐拉方法改進后的求解偏微分方程的常用方法,這種方法不僅計算效率高,而且穩定性好。格式的推算過程如下:

假設求解方程為

(15)

式中F是對空間變量的微分算子,則修正的四階Runge-Kutta格式為

(16)

1.3 誤差估計

(17)

將式(17)代入式(6),所求得組合型超緊致差分格式的一階導數及二階導數對應的截斷誤差為:

(18)

(19)

使用組合型超緊致差分格式的好處是在每一個網格點上存在一個一階和二階連續導數的多項式。本文比較了組合型超緊致差分格式和現有廣義格式的一階導數和二階導數的截斷誤差:

(20)

式中參數α,β,a,b,c在各種格式中取不同的值(表1,表2)。本文發現在各種方案中,組合型超緊致差分格式的截斷誤差最小。

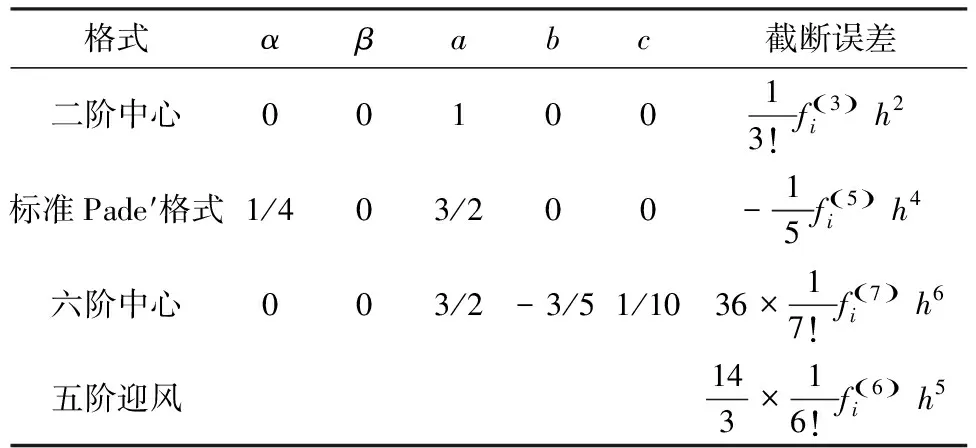
表1 不同格式一階導數的截斷誤差

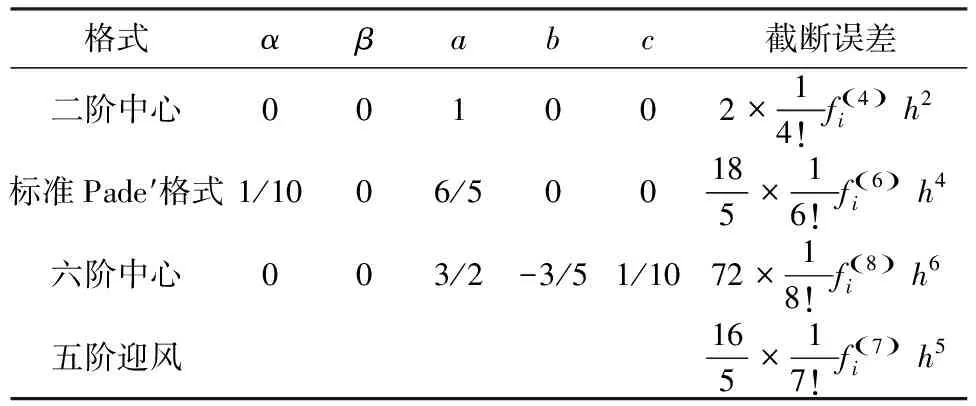
表2 不同格式二階導數的截斷誤差

2 數值算例

誤差范數L1和L2的定義為:

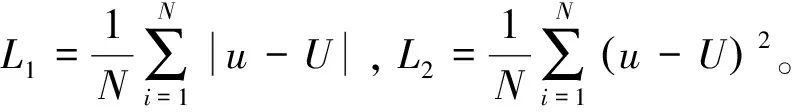
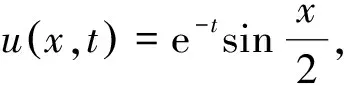
對給出的數值算例,計算誤差范數L1和L2,并采用四種方法進行數值模擬,對其數值結果進行誤差分析和對比,結果見表3,本文所使用方法效果最佳,由此證明所提方法的有效性和可行性。

表3 0.5 s時刻精確度測試結果(N=10)

用本文提出的式(6)—式(8)和式(16)計算算例, 圖1—圖3給出了不同時刻數值解與精確解的對比圖,可以看出,數值解與精確解吻合很好,表明本文給出的數值格式是可行的,并且精度較高。

(a)精確解(b)數值解圖2 0.5 s的精確解與數值解

(a)精確解(b)數值解圖3 1 s的精確解與數值解

3 結論

本文研究了組合型超緊致差分方法和四階Runge-Kutta方法,并將其運用于四階Cahn-Hilliard方程的數值求解,通過研究與分析,得到如下結論:

1)使用泰勒級數展開鎖定差分格式系數,得到本文的組合型超緊致差分格式精度更高,誤差更小。

2)在邊界點處有效地達到了降階,并提高了精度。

3)通過數值算例驗證了數值格式的有效性。

4)預估該方法可應用于高階偏微分方程的數值求解。