基于GWO-XGBoost 的工業污水水質關鍵數據預測算法

牛景輝

（天津石油職業技術學院，天津 301607）

在工業污水處理領域，對水質指標的變化進行預測能更好地優化工業污水設施管理水平〔1-3〕。以實際工業污水處理過程的pH 和濁度為例，進出水水質的預測任務對污水處理工藝控制非常關鍵。對污水指標預測的相關理論研究近年來獲得了國內外高度關注。預測工業污水數據的方法主要分成兩大類，一類是基于水質處理過程建模的方法〔4-5〕，另一類是數據驅動預測方法〔6-7〕。水質處理的機理建模存在較多的非線性參數，機理數學建模過程復雜繁瑣，預測精度容易受到數據噪聲的干擾影響，且一般只能針對特定污水處理工藝過程進行，遷移性具有很大的限制。隨著污水處理的計算機自動化控制技術的發展，數據信息化積累了大量的污水處理監測數據。如何有效地利用污水處理的監測數據是亟需解決的問題。有許多數據驅動類方法被引入污水處理數據的預測中，如：回歸統計、時間序列分析、BP 神經網絡、長短時回憶網絡等方法可以對數據做到較為準確的預測。N. BHOJ 等〔8〕提出了融合深度學習算法的時間序列預測方法，該方法可識別數據特征和異常情況，能夠較準確地預測數據變化趨勢，并指出利用優化算法提升預測算法效果具有很大空間。Fenghua YANG 等〔9〕將提出了基于長短時回憶神經網絡算法預測水質的方法，該方法用于預測水質處理藥劑的投加量，提升了污水處理的運行管理水平。K. BANERJ 等〔10〕研究了使用SVM 回歸等多種機器學習算法，該方法結合了多種水質數據變量，實現了較為準確的水質數據變化預測。唐亦舜等〔11〕將非線性自回歸算法用于神經網絡模型進行優化，實現了對污水pH 和DO 等水質數據良好的預測效果，但是調整參數比較繁瑣。何丹等〔12〕通過粒子群算法改進BP 神經網絡進行污水處理過程的預測，使神經網絡預測算法的收斂速度進一步提升，跳出局部極值點，實現了算法預測效果的優化。王立輝等〔13〕基于灰狼優化（Grey Wolf Optimizer，GWO）算法改進的循環神經網絡能夠減少參數調整的復雜程度進而執行數據預測，在水流量預測中發現具有良好的效果。王春玲等〔14〕對水質的COD數據采用了XGboost 構建預測算法模型，并且利用了主成分分析算法進行了數據預處理，提升了算法訓練速度和水質預測精度，與多種機器學習算法對照，表明XGBoost 算法預測效果最優。

因此，筆者提出了通過XGBoost 模型構建污水的關鍵水質數據預測算法，另外針對其需要調整參數較多的問題，采用了灰狼優化算法進行模型參數的優化調整。此外考慮到水質數據的復雜隨機非線性特征，數據經過預處理后，預測算法能夠更好地提取水質數據的特征，最后通過與默認參數的XGBoost、LSTM 算法進行預測對照，檢驗了該算法的穩定性和能達到預期效果的能力。

1 預測模型方法

1.1 灰狼優化原理

狼群有其獨特的狩獵方式，GWO 通過研究其行為模式進行了數學建模。借由模仿狼群的移動模式來實現目標的最優化。在種群內部，個體有α、β、δ3 個等級，分別是頭狼、第二級別、第三級別。其圍獵過程如下：

第一步是包圍獵物：

式中：t——當前的代數；

A、C——協同系數向量；

Xp——獵物的位置向量；

X——灰狼的位置向量；

D——灰狼與獵物之間的坐標距離。

A、C的計算方法如下：

式中，a是收斂因數，伴隨迭代次數變多，從2 線性降低到0；r1、r2是［0，1］的隨機數向量。

第二步是抓捕獵物：由于獵物的坐標未知，可以知道目標的最優值也未知。采用以下思路：假定α是最接近獵物的，β、δ其次，用式（5）～式（7）測算α、β、δ與獵物的距離。伴隨著不斷更新α、β、δ狼的坐標〔式（8）～式（10）〕來召喚其他灰狼不斷接近獵物〔式（11）〕，最后認定α狼的坐標就是獵物的坐標。為增加隨機性，減小陷入局部極值的概率，在位置迭代計算公式上增加了隨機項rand。因本研究中所有的參數被歸一化到［0，1］區間內，所以隨機項為［0.01，0.1］之間的隨機數。其計算式如下：

式中，Xα（t）、Xβ（t）、Xδ（t）分別為t代時α、β、δ的位置。

1.2 XGBoost 算法原理

XGBoost 即極端決策提升樹算法，由GBDT 提升樹算法模型演變改造優化而來〔15-16〕，通過反向疊加算法，集成Boost 策略改進多個弱學習算法融合成1 個高度精確的學習預測算法，將多個學習器結合與預測實際值進行評估誤差疊加加權求和不斷迭代，改進了回歸分類決策樹的結構，從而最終實現提升模型的預測效果。XGBoost 算法最重要的核心問題是決策樹疊加融合評估誤差的目標函數：

式中，Loss是實際值與預測值偏差的損失函數，yj是預測數據的實際值，y?i是上一個決策樹算法的結果，x是輸入數據，從而擬合多個決策樹的算法結果，而fm是決策樹所采用的近似函數，γ是對決策數的結果正則化改進懲罰系數項，而基本的決策樹近似求取函數為：

XGBoost 模型優化調整的主要問題是以所需要預測數據樣本的特征為輸入，訓練改進各項函數的系數調整取值，并且最優化的數據預測結果為目標，建立最優化的XGBoost 模型算法預測所需數據的結果。在XGBoost 模型中，通常對模型預測表現影響較大的超參數有：最大生成樹計數、學習率、樹的最大深度和最小葉子節點樣本權重之和。為降低在參數調優過程中產生計算工作量過大的風險，僅使用GWO 優化以上4個參數。

2 工業污水水質關鍵數據GWO-XGBoost預測算法構建

XGBoost模型超參數多，難以同時優化。通過GWO優化模型超參數的取值方法進一步增強XGBoost 模型的預測能力。在XGBoost 模型參數優化階段，狼群種群個體的適應度函數為該個體參數下XGBoost 模型的預測結果與真實數據的均方根誤差（RMSE）。當RMSE達到全局最小值時，認為GWO 已經尋找到了XGBoost的最佳參數組合。

使用GWO 優化XGBoost 算法流程示意如圖1所示。

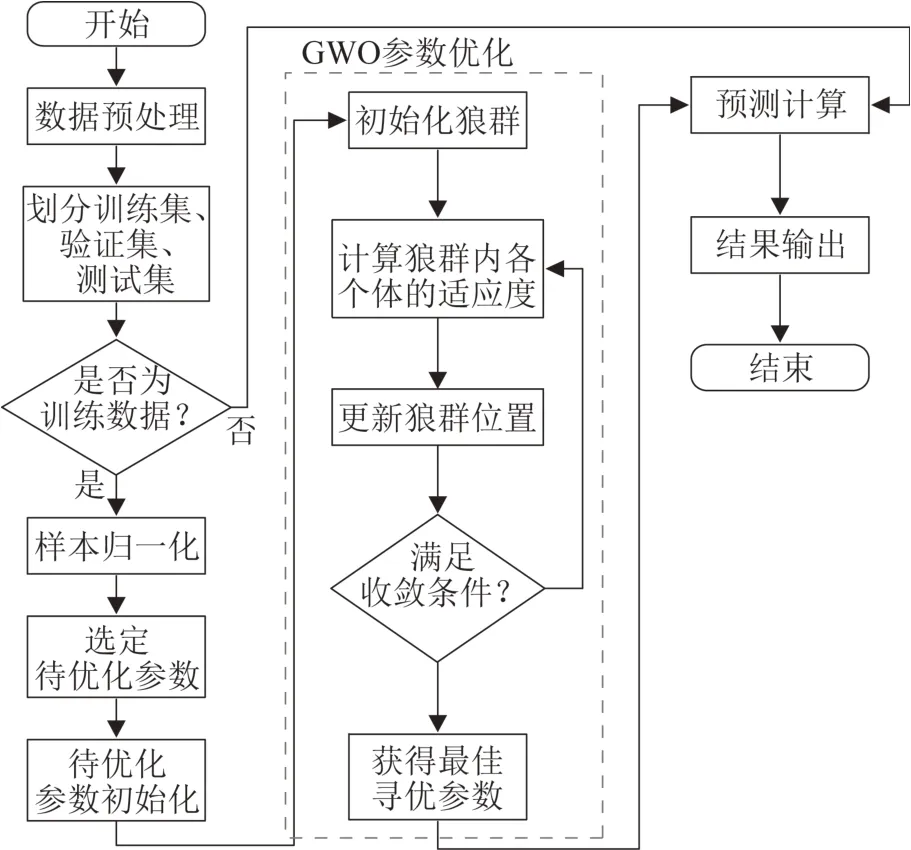
圖1 使用GWO 優化XGBoost 算法流程示意Fig.1 Using GWO to optimize the XGBoost algorithm process

首先隨機初始化GWO算法的種群，確定搜索范圍。把當前輪的種群所指代的參數數據按照順序導入XGBoost 模型，通過對XGBoost 模型的訓練，獲得XGBoost 模型的計算結果。再使用驗證集對此次完成訓練的模型進行求證，最后獲得適應度函數。以適應度函數的大小評估種群內部各個體的水平，并計算得到下一輪的迭代種群內各個體的移動方向。如果滿足算法收斂條件，則停止迭代，輸出XGBoost 優化后的參數。若不滿足收斂條件，則按照迭代規則，更新種群內部各個個體的位置，重復上一輪操作。

在啟動GWO 算法前，首先確定XGBoost 參數的取值范圍，其中最大生成樹數目，取值范圍為100～1 500；學習率默認值初始設置為0.30，取數區間最小值為0.01、最大值為0.5；樹的最大深度一般初始值設定為6，取數區間最小值為3、最大值為12；最小葉子節點樣本權重和一般默認數值設定為1，取數區間最小值為1，最大值為10；確定取數區間后，將所有參數進行Min-Max歸一化，即種群的所有個體為四維空間內的向量。同時設置狼群數量為20，最大迭代次數為200 次。

3 數據處理與數據集的構建

為驗證所提算法的有效性，選取了某處水體斷面的部分關鍵水質監測數據。選區的樣本數據時間跨度從2019 年1 月1 日到2019 年8 月9 日，總共221 個自然日合計2 652 個時間點，采樣間隔為120 min。在數據預處理環節使用了四分位距法移除了異常數值點，并采用多項式插值法（二階）補齊了缺失數據。數據包含了pH、溶解氧、濁度、總磷和總氮等各項指標記錄13 260條。訓練集為前2 232 個時間點的數據（186個自然日），驗證集包括了288 個時間點的數據（24 個自然日），測試集為最后120 個時間點的數據（10 個自然日）。

對所有的原始數據采用滑動窗口的方式進行構造訓練集、驗證集與測試集。本研究中，數據滑窗寬度取l=12，滑窗步長取s=1。訓練集數據和驗證集、測試集數據分別進行了均值方差歸一化（化為均值為0，方差為1 的數據）與最值歸一化（數據被映射到［0，1］區間）。

4 預測算法對比分析

本次優化XGBoost模型的4個重要超參數，分別是：最大生成樹數目（n estimator）、學習率（learning rate）、樹的最大深度（max depth）和最小葉子節點樣本權重和（min child weight）。最大生成樹數目取數區間最小值為100，最大值為1 500，默認值為500；學習率默認值為0.30，取數區間最小為0.01，最大為0.5；樹的最大深度默認值為6，取數區間最小為3，最大為12；最小葉子節點樣本權重和默認值為1，取數區間最小為1，最大值為10。

首先對XGBoost 上述4 個超參數進行初步手動調參，得到手動調參后的初始值如表1 所示，其余超參數則采用默認值。同樣地，對于對照組LSTM 也進行了手動調參，得到的參數值如表1 所示。為了驗證GWO對XGBoost 預測表現的提升效果，在測試部分與手動調優后的XGBoost、LSTM 相比較，將三者分別用于預測同一水質指標的變化。使用GWO 優化XGBoost 的初始超參數與手動調優后的XGBoost 相同。

表1 各算法初始參數Table 1 Initial parameters of each algorithm

測試集的數據時間跨度從2019 年7 月30 日開始到8 月9 日為止，共計10 個自然日（包括了用于預測7月31 日指標的輸入數據）。GWO-XGBoost、XGBoost與LSTM 分別用于預測pH、溶解氧、濁度、總磷和總氮的預測結果如圖2～圖6 所示，各算法的RMSE 與決定因數（R2）如表2 所示。

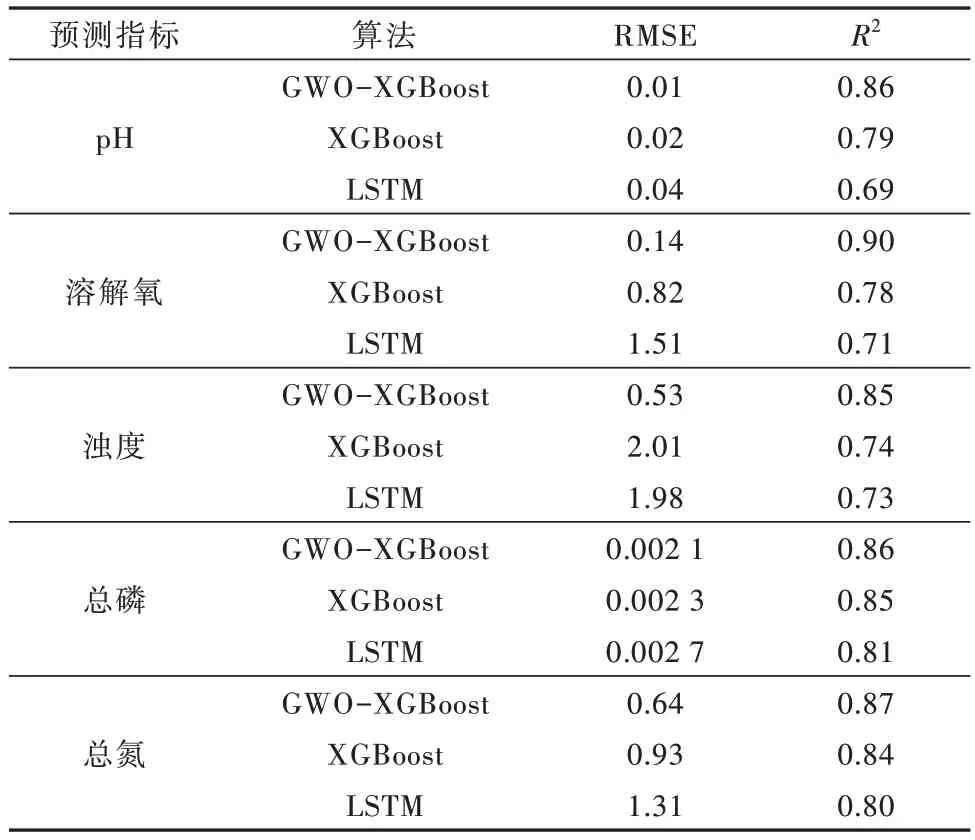
表2 各算法在不同水質指標下的預測表現比較Table 2 Comparison of the prediction performance of the algorithms for different water quality indicators

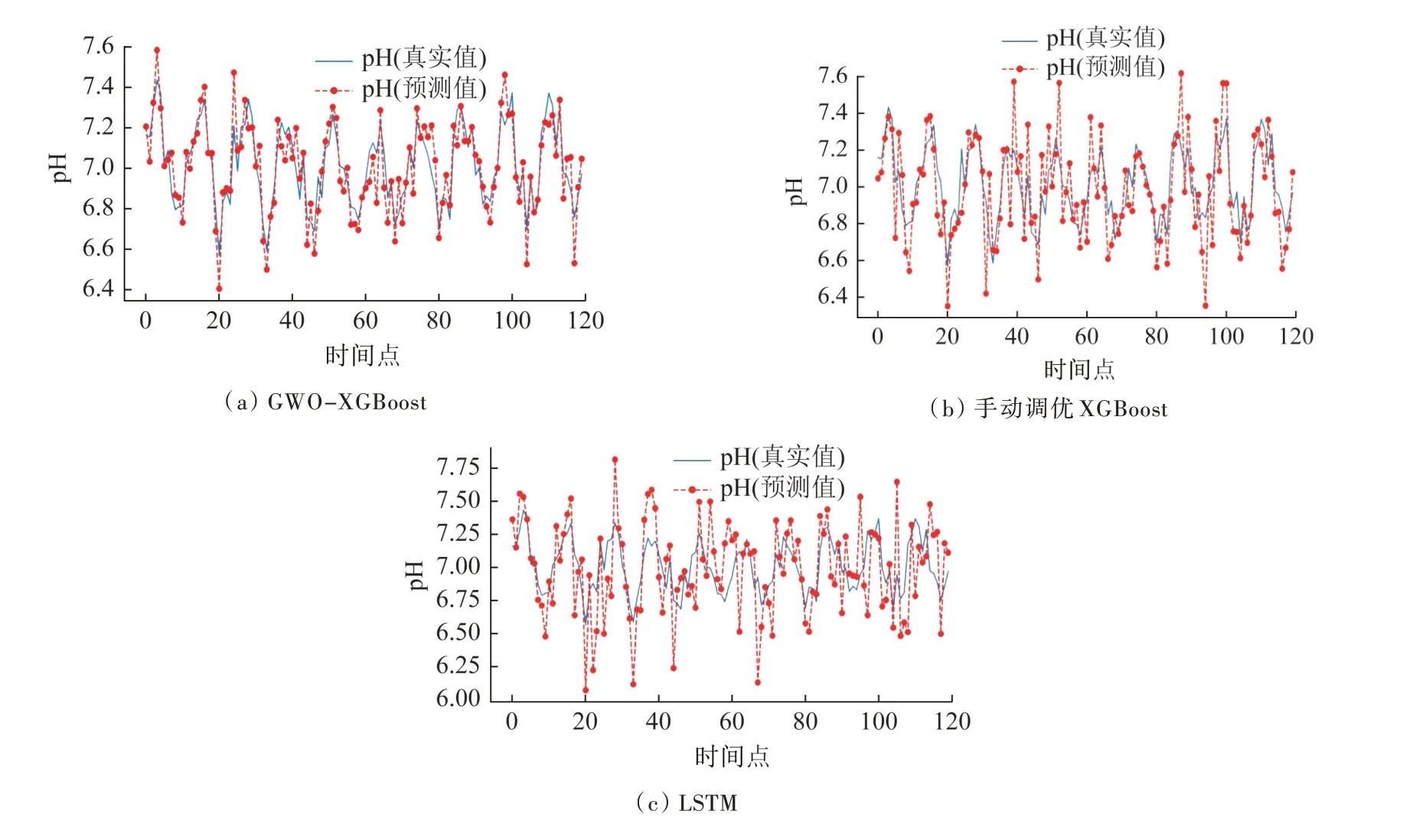
圖2 用于pH 指標的預測結果Fig.2 Prediction results for pH

由實測結果可知，目標斷面pH 在7.0～7.5 之間波動。預測結果如圖2 所示。GWO-XGBoost、XGBoost與LSTM 的R2分別是0.86、0.79 和0.69，RMSE 分別為0.01、0.02 和0.04。

在預測斷面的溶解氧數值時，目標斷面溶解氧在5.1～9.5 mg/L 之間波動。預測結果如圖3 所示，GWOXGBoost、XGBoost 與LSTM 的R2分別為0.90、0.78 和0.71，RMSE 分別為0.14、0.82 和1.51。

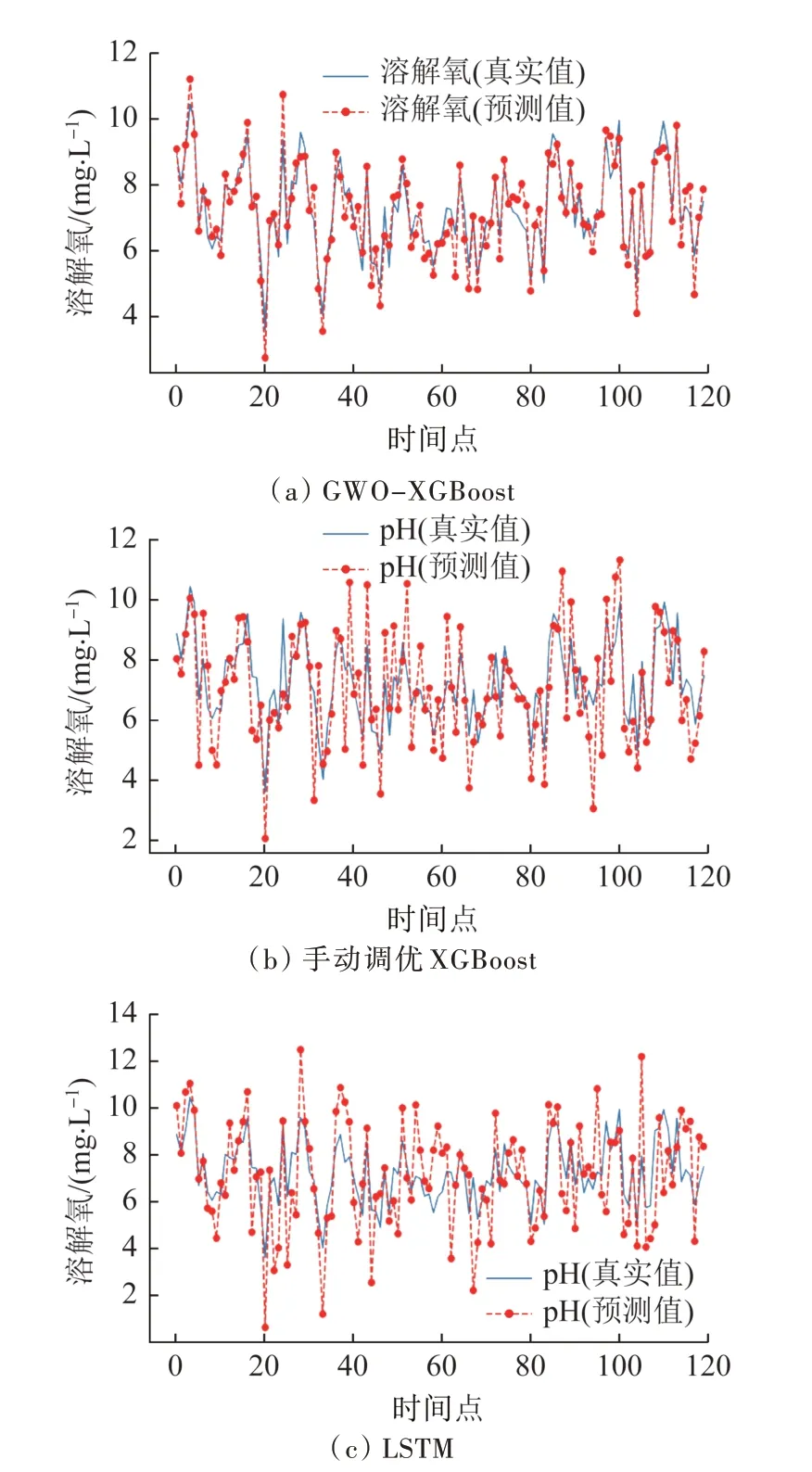
圖3 用于溶解氧指標的預測結果Fig.3 Prediction results for dissolve oxygen

在預測斷面的濁度數值時，目標值在1.1～12.2 NTU之間波動。預測結果如圖4 所示，GWO-XGBoost、XGBoost 與LSTM 的R2分別為0.85、0.74 和0.73，RMSE分別為0.53、2.01 和1.98。

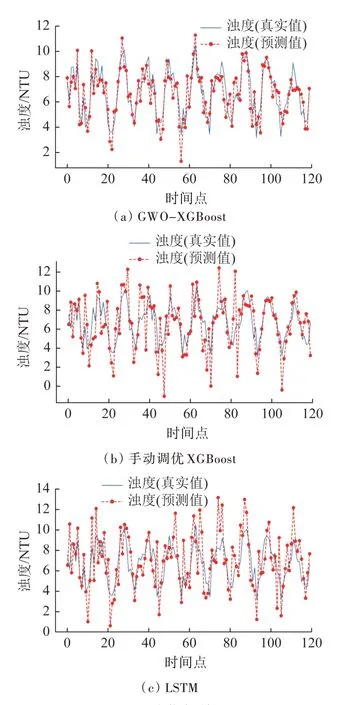
圖4 用于濁度指標的預測結果Fig.4 Prediction results for NTU

在預測斷面的總磷數值時，目標斷面總磷在0.009～0.053 mg/L 之間波動。預測結果如圖5 所示，GWO-XGBoost、XGBoost 與LSTM 的R2分別為0.86、0.85和0.81，RMSE分別為0.001 9、0.002 3和0.002 7。

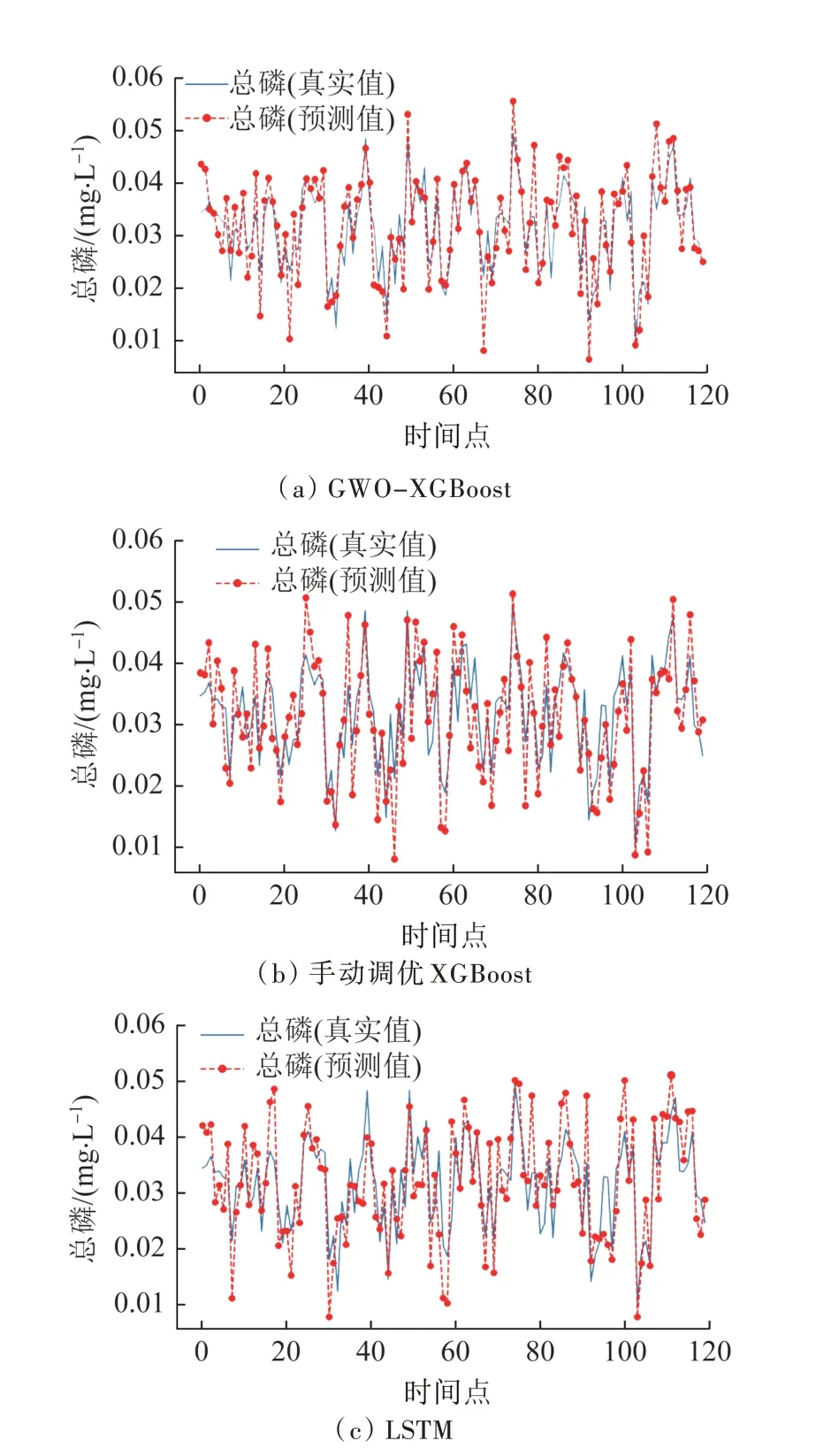
圖5 用于總磷指標的預測結果Fig.5 Prediction results for TP

在預測斷面的總氮數值時，目標斷面總氮質量濃度在2.2～12.3 mg/L 之間波動。預測結果如圖6 所示，GWO-XGBoost、XGBoost 與LSTM 的R2分別為0.87、0.84 和0.80，RMSE 分別為0.64、0.93 和1.31。

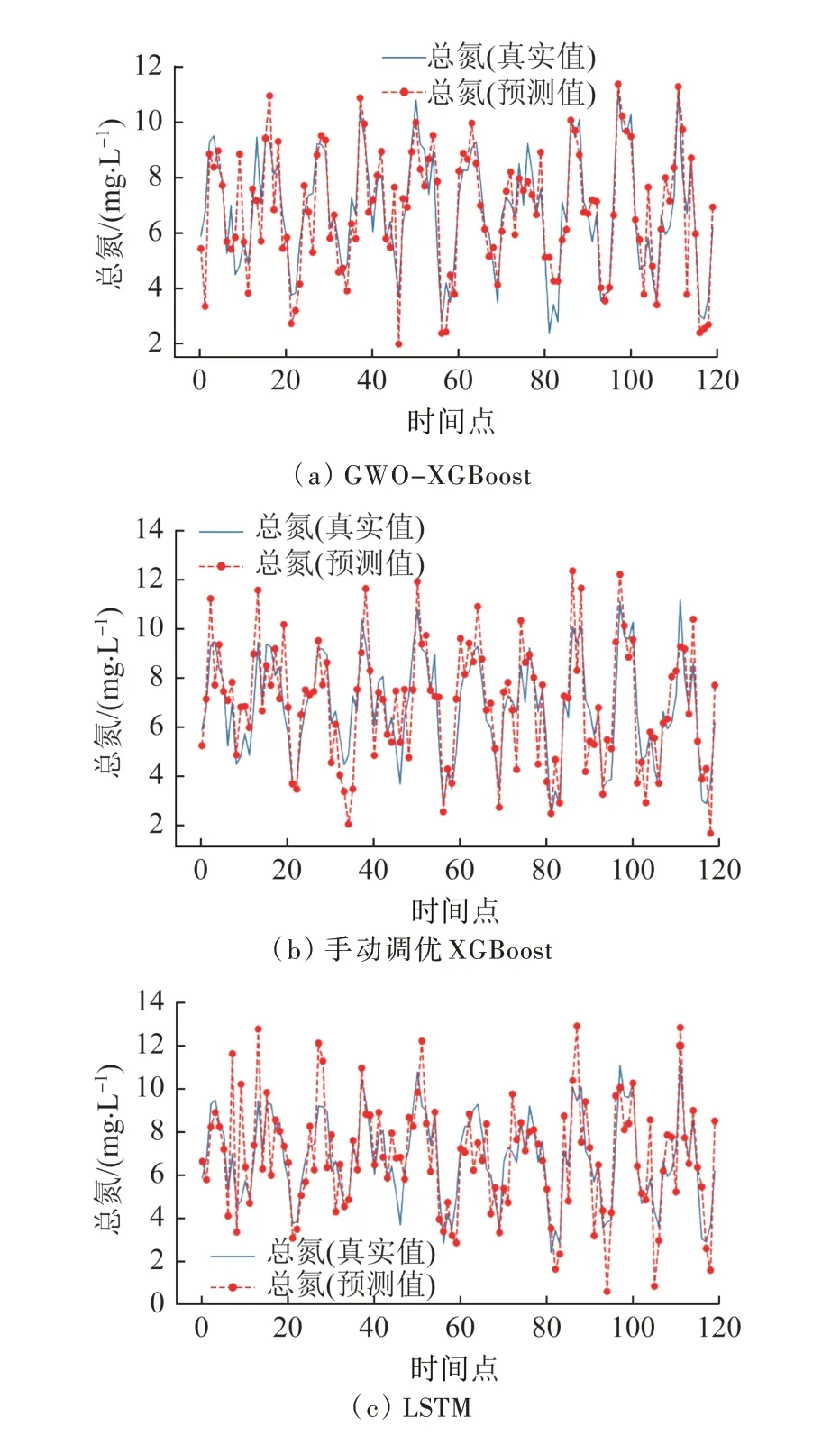
圖6 用于總氮指標的預測結果Fig.6 Prediction results for TN

由圖2～圖6、表2 可知，基于GWO 算法優化的XGBoost 模型對目標斷面的pH、溶解氧、濁度、總磷和總氮的預測值與實測值的變化趨勢基本保持一致，并且R2均達到0.71以上。在預測斷面的pH時，結合RMSE值可知：與默認參數的XGBoost 模型相比，經過超參數優化后，基于GWO 算法優化的XGBoost 模型的預測精度和自相關檢驗通過率均得到顯著改善；各時間序列預測結果出現的差異主要是由原始時間序列的波動和量級的影響所致。

5 結論

污水水質數據具有很強的隨機性和非線性特征，一般的預測算法難以實現高精度的預測，但是更高精度的預測模型對優化污水處理運行管理有重要指導作用。本研究利用灰狼算法優化后的XGBoost模型對污水的關鍵水質數據進行了預測。首先，對GWO 進行了簡化，降低了計算復雜性，同時強化了隨機性，降低了GWO 在迭代過程中容易陷入局部最優區域的風險。其次，將水質時間序列數據進行了預處理，選取了其中部分對XGBoost模型表現影響大的參數，并使用GWO 進行了優化。最后，由GWO 優化后的XGBoost模型與手動調參的XGBoost、LSTM 進行了對比，證明由GWO 優化后的XGBoost模型有著更高的預測精度和更強的泛化能力。與手動調參的XGBoost模型相比，由GWO 優化過的XGBoost模型在預測pH、溶解氧、濁度、總磷和總氮的決定因數R2分別提高了8.86%、15.38%、14.86%、1.18%和3.57%，實現了較為準確的水質關鍵數據預測。