基于自抗擾控制器的永磁同步電機直接轉矩控制

李少朋,謝源,張凱,賀耀庭

(上海電機學院 電氣學院, 上海 201306)

0 引 言

永磁同步電機擁有響應速度快、效率高、輸出轉矩大以及調速范圍廣的特點[1-2]。對于永磁同步電機的控制策略,目前較為常用的是矢量控制和直接轉矩控制。矢量控制策略就是對變流器的電流、電壓進行控制,獲得理想的電壓、電流,使得永磁同步電機按照需求得到控制,直接轉矩控制策略是對轉矩和磁鏈進行直接控制,控制結構簡單[3-4]。對比兩種控制策略,直接轉矩控制結構簡單,動態響應快,控制效果突出,優于矢量控制。但是直接轉矩控制存在轉矩及磁鏈脈動較大的問題,使得其應用受到了一定的限制。

針對這些問題,需要對傳統的DTC做一些優化,來提高DTC的控制性能。傳統的DTC策略由于滯環控制的影響,對于轉矩的波動影響很大。為了解決這問題,提出了一種復合轉矩調節器[5],通過設計新的磁滯帶與恒定磁滯帶相結合形成一種復合控制策略,減少了轉矩的偏差和時間延遲,降低了轉矩的脈動。但文獻[6-7]中摒棄了傳統的開關表和滯環控制器,對于輸出的電壓矢量使用空間矢量調制合成,保證了開關頻率的固定。基于空間矢量條件的控制策略,雖然保證了開關頻率的穩定性,但是整個系統還是基于PI控制,PI控制器對于PMSM系統的非線性要求還不能很好地滿足。在外部干擾下,PI控制器對于系統的快速變化不能有很快的響應,系統的魯棒性較差。當前對于PI控制器的改進也有許多的方法,如將PI控制器替換為滑模控制器或者在PI的控制基礎上引入PI參數的在線調節以此來優化PI控制器。文獻[8-9]提出了基于二階滑模的直接轉矩控制策略并證明其控制性能的穩定,結合空間矢量調制技術,在一定程度上改善了PI控制器魯棒性差的缺陷,也保證了開關頻率的穩定。雖然滑模控制結構魯棒性較強,但其本身的抖動特性并未完全消除。

為了保證PID控制器的優點,并使其滿足非線性系統的控制要求,中國科學院韓京清研究員在PID經典控制器的基礎上,深入研究現代控制理論提出了自抗擾控制器[10]。ADRC由于是在PID控制器為基礎發展而來,保留了PID控制器的優點并且結合了非線性要求,從而提出一種新型的、非線性的實用控制策略。自抗擾控制技術不依賴被控對象的精確數學模型,可以通過對系統狀態的觀測,得到系統擾動并加以補償消除誤差,使得控制量得到精確的控制[11]。

文中研究對象為PMSM,提出一種基于自抗擾控制的直接轉矩控制策略。為了改善PI控制器的缺陷,文中采用ADRC取代PI控制器,設計基于ADRC的轉速環和磁鏈環以及轉矩環,并結合空間矢量調制技術,在滿足系統的非線性要求下,還保證了開關頻率的穩定。實驗結果表明：采用自抗擾控制的直接轉矩控制方法有很好的跟蹤性能,抗負載擾動能力,使得轉矩和磁鏈脈動大大降低,并且消除了轉速的超調。

1 永磁同步電機的數學模型

以三相表貼式永磁同步電機(SPMSM)為研究對象,采用文獻[5]中的永磁同步電機的d-q軸的數學模型,永磁同步電機的d-q軸數學模型為：

定子電壓方程：

(1)

定子磁鏈方程：

(2)

式中ud、uq為定子電壓在d-q軸上的分量;id、iq為定子電流在d-q軸的電流分量;ψd、ψq為定子磁鏈在d-q軸上磁鏈分量;ωe為電角度,R為定子電阻。永磁同步電機的數學模型中忽略了電動機的鐵芯飽和、磁滯、渦流損耗等影響因素[6]。

將式(2)帶入到式(1),可得定子電壓方程為：

(3)

電磁轉矩方程：

Te=1.5pniq[id(Ld-Lq)+ψf]

(4)

式(3)中Ld、Lq為定子電感在d-q軸分量,式(4)中ψf為轉子磁鏈,pn為極對數,ωr為轉速,B為摩擦常數。其中式(4)是針對三相內置式永磁同步電機建立的數學模型,而對于三相表貼式的永磁同步電機,定子電感滿足Ld=Lq=Ls的條件,則此表貼式永磁同步電機模型的電磁轉矩方程為：

Te=1.5pnψfiq

(5)

2 基于ADRC控制器設計

2.1 ADRC控制理論

ADRC由跟蹤-微分器(TD)、擴張狀態觀測器(ESO)以及非線性狀態誤差反饋控制率(NLSEF)三部分組成,其中ESO是ADRC的核心組成部分[11]。系統的控制效果取決于ESO總擾動的觀測和NLSEF的補償。

以一階系統為例,假定一階系統的狀態方程如下：

(6)

式中w(t)為外擾作用;f(y,w(t),t)為綜合了外擾和內擾的總擾動;u為控制量,b為控制量的補償因子。令x=y,將式(6)轉換成狀態方程：

(7)

ADRC控制的目的是將式(6)變成形如y=u0的線性積分串聯標準型,使得控制更加簡單。式(7)狀態方程經過TD過程,得到的數學模型為：

(8)

式中v1為給定轉速的跟蹤值,v為系統給定的參考信號。將跟蹤值和給定參考值的誤差經過fhan函數的處理得到v的近似微分信號。

式(8)中非線性函數fhan(x,r,h)定義如下：

(9)

(10)

式中r為TD中跟蹤速度因子。r值越大跟蹤速度越快,反之越慢,但是r大小要根據過渡過程的快慢及系統的承受能力來決定。h為函數中的濾波因子,對于控制過程中的噪聲起過濾作用,其取值大小與系統的采樣周期有關。

式(11)中所示一階系統的ESO數學模型為：

(11)

式中z1為系統輸出y的跟蹤信號;z2為ESO對系統擾動的估計值,其中包括系統的外擾動和內擾動。ESO的觀測值和擾動估計值的準確性對于自抗擾控制器的控制性能有決定性作用。α1、α2為非線性因子,取值規律為α1=0.5α2,由這個取值特點進行參數的調節;δ為濾波因子,δ>0;β01、β02為可調參數;e為TD跟蹤信號與z1觀測信號誤差值。Fal(e,α,δ)為非線性函數,函數表達式定義如下：

(12)

式(7)所示的一階系統的NLSEF的數學模型如下：

(13)

式中β1為可調參數,δ1為濾波因子,α3為非線性因子。NLSEF中的三個可調參數與ESO中的可調參數相互獨立,可以分別整定。

(14)

式(14)中對于NLSEF輸出量u給出了兩種不同的控制結構。其中b=1時的控制結構,可以針對歸一化后的對象,即串聯積分器的形式,增益為1。式中b≠1時的控制結構,是對于當前的增益有相對精確的判斷,并且其增益不是1。對于控制量輸出結構的劃分,目的是對于系統的控制有一個整體的把握,提高控制精度和控制性能。

2.2 ADRC控制器設計

由永磁同步電機的運動方程可得：

(15)

由式(15)可以得出對系統外部干擾的影響量為TL,TL的變動為系統的外擾;B、J為系統建模過程中的不確定項,即為內擾。這些擾動會對系統的控制精度,系統的響應速度產生影響。基于ADRC原理,將系統受到的擾動和記為：

(16)

基于電機的運動方程,轉速環控制輸出的信號為電磁轉矩的參考信號,得出速度控制環的控制律為：

(17)

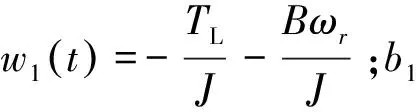
基于ADRC理論,擾動項通過ESO估計出來,不需要辨識其本身的數學表達式,只要通過ESO實時的估計出擾動量,并將其進行精確地補償,就可以使得系統得到相應的控制。

當定子磁鏈的矢量方向與d軸方向一致時,磁鏈幅值ψr可以表示為：

(18)

根據速度環的控制方式得到磁鏈環的控制規律為：

(19)

式中的w2(t)為磁鏈環控制中的擾動項,w2(t)=-Rsid。

文中在磁鏈控制律中加入了補償因子b2,所以最終的磁鏈環控制律為：

(20)

式中的補償因子b2是根據系統運行中的反饋情況以及工程經驗進行整定,用來補償系統建模的不準確度以及在實際運行過程中的不確定影響。

假定定子磁鏈的幅值為一常數,此時電磁轉矩的微分形式如下：

(21)

將式(3)帶入到式(21)中,可得：

(22)

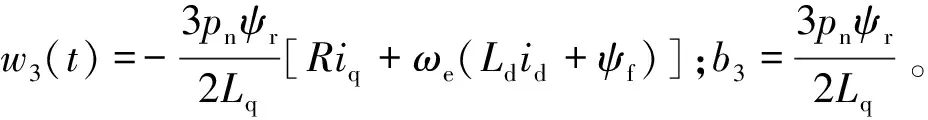
(23)

3 實驗仿真及結果分析

為驗證上述理論的正確性及控制方法的有效性,在MATLAB/Simulink仿真軟件環境下,對系統進行了建模與仿真分析研究,圖1為控制框圖。

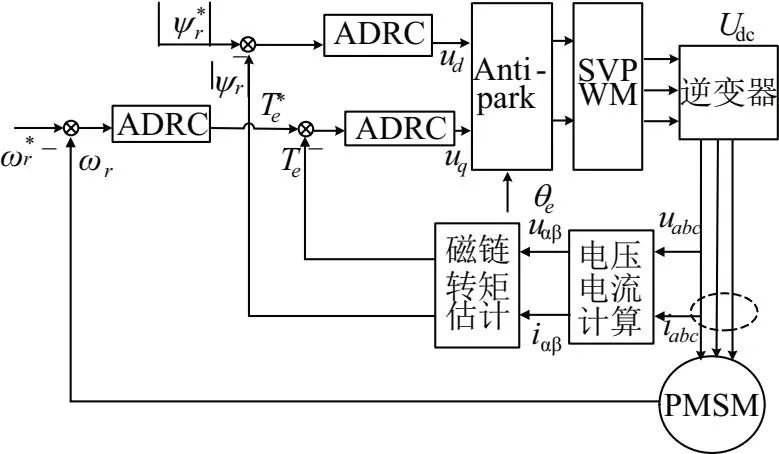
圖1 基于ADRC的直接轉矩控制框圖

為了驗證上述控制策略的有效性,文中基于加拿大Opal—RT公司開發的一套工業級的仿真軟件RT-LAB搭建了半實物仿真平臺。MATLAB/Simulink中搭建PMSM模型和逆變器模型,下載到RT-LAB中進行實時的仿真;控制部分采用DSP開發套件TM320F28335進行相應信號的采集。半實物平臺搭建如圖2所示。

圖2 半實物仿真平臺

電機參數如下：極對數np=4,定子電感Ld=Lq=8.5 mH,定子電阻R=12.9 Ω,永磁磁鏈ψf=0.66 Wb,轉動慣量J=0.0008 kg· m2,粘滯摩擦系數B=0.001 N· m· s,額定轉速為750 rad/min,額定電磁轉矩TN=3 N·m,額定電壓UN=380 V。

為了驗證磁鏈控制器和轉矩控制器的跟蹤精度、抗負載擾動能力和負載擾動后的恢復能力,做了如下實驗：給定轉速n=600 r/min,電機在初始負載轉矩為0 N· m,0.2 s后果負載轉矩為1.5 N·m。

圖3為ADRC_DTC策略和傳統PI_DTC控制策略的轉速對比仿真波形。由圖3可知,ADRC_DTC策略系統響應與PI_DTC策略響應時間大致相同,但是ADRC_DTC策略沒有超調并且很快跟隨系統,動態性能好。突加負載時,轉速有極小的波動,波動范圍在600 r/min～599.2 r/min之間。傳統PI_DTC策略,響應過程有超調并且超調較大,并且其跟隨系統的動態性能低于ADRC_DTC策略,達到穩定運行狀態所需時間長。突加負載時,轉速有較大幅度波動,轉速波動范圍在600 r/min到590 r/min之間,轉速波動遠大于ADRC_DTC策略。由此也說明了ADRC_DTC的動態性能好,對于系統的穩定性和抗干擾性有了很大的提高。圖4為上述控制策略的轉速實驗波形,圖4(a)為ADRC_DTC策略的轉速實驗波形,圖4(b)為PI_DTC策略的轉速實驗波形。從這兩種策略的實驗波形中可以看出,轉速的響應以及抗干擾的變化與仿真結果吻合,證明了所提出的控制策略具有很好的可行性。

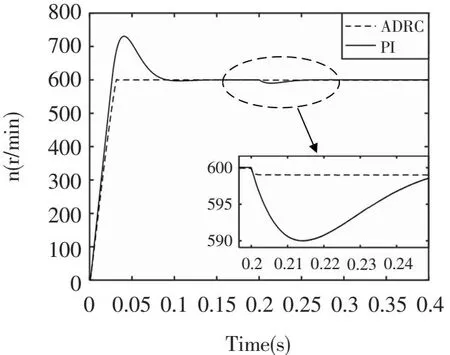
圖3 ADRC_DTC和傳統PI_DTC轉速仿真圖

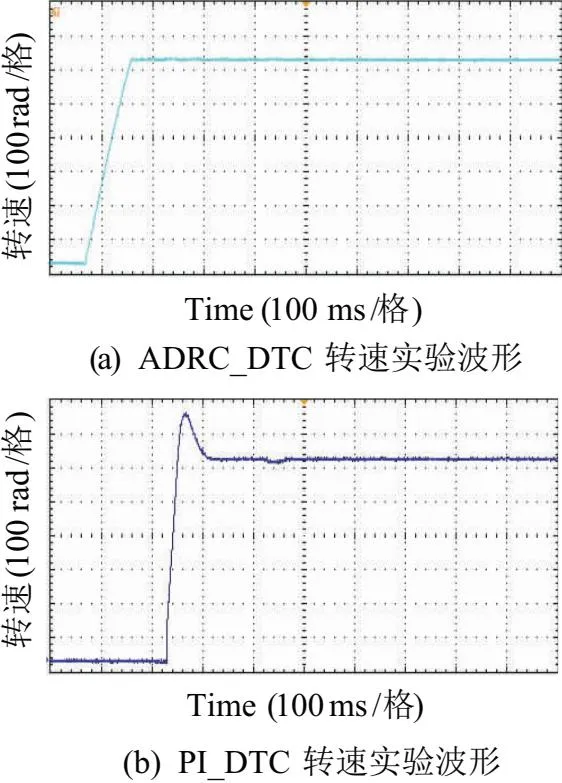
圖4 ADRC_ DTC策略和傳統PI_DTC策略轉速實驗波形圖

圖5為ADRC_DTC策略和傳統PI_DTC控制策略的轉矩對比仿真波形。從圖5的整體走向中可以看出,ADRC_DTC策略響應快,并且可以很快達到穩定;PI_DTC策略響應過程中有較大的波動,穩定時間長,并且在受到外部干擾時達到穩定的時間長于ADRC_DTC策略。

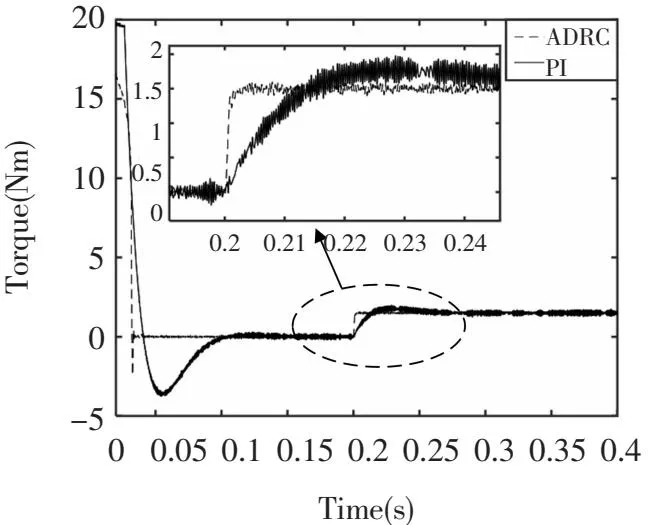
圖5 ADRC_DTC和傳統PI_DTC轉矩仿真圖

從圖5中的波形放大部分可以看出,在0.2 s時突加負載擾動,ADRC_DTC策略轉矩波動小并且迅速穩定達到所給定的轉距值,從波形放大部分可以得到轉矩大致波動范圍是1.4 N· m～1.6 N· m。PI_DTC策略,在0.2 s時加負載轉矩擾動,轉矩波動較大,并且達到穩定的時間較長。從波形放大部分可以看出轉矩波動的大致范圍為1.98 N· m到1.3 N· m,波動幅值很大。通過對兩種控制策略的轉矩仿真結果的分析,可以看出ADRC_DTC策略可以極大地降低轉矩脈動,并且在受到外部負載轉矩擾動時可以迅速地到達穩定,提高了系統的控制精度和系統的穩定性,ADRC對電磁轉矩脈動的抑制效果明顯。

圖6為上述控制策略的轉矩實驗波形,圖6(a)為ADRC_DTC策略的轉矩實驗波形,圖6(b)為PI_DTC策略的轉矩實驗波形。從這兩種策略的實驗波形中可以看出,轉矩的響應以及抗干擾的變化與仿真結果吻合。

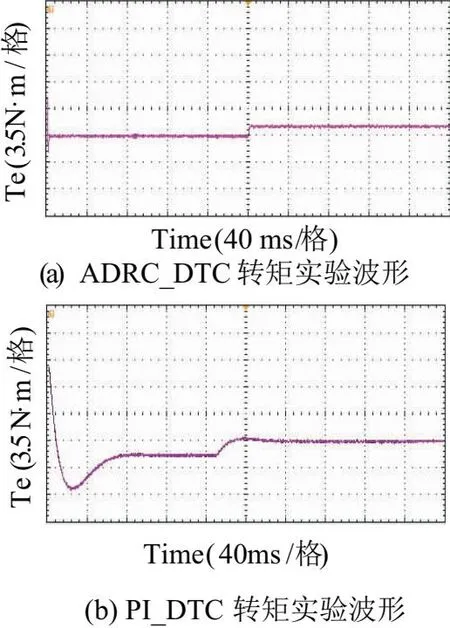
圖6 ADRC_ DTC策略和傳統PI_DTC策略轉矩實驗波形圖

圖7為ADRC_DTC策略和傳統PI_DTC控制策略的磁鏈對比仿真波形。從圖7中的整體磁鏈波形可以看出ADRC_DTC策略的磁鏈響應和磁鏈脈動幅值均優于PI_DTC策略。

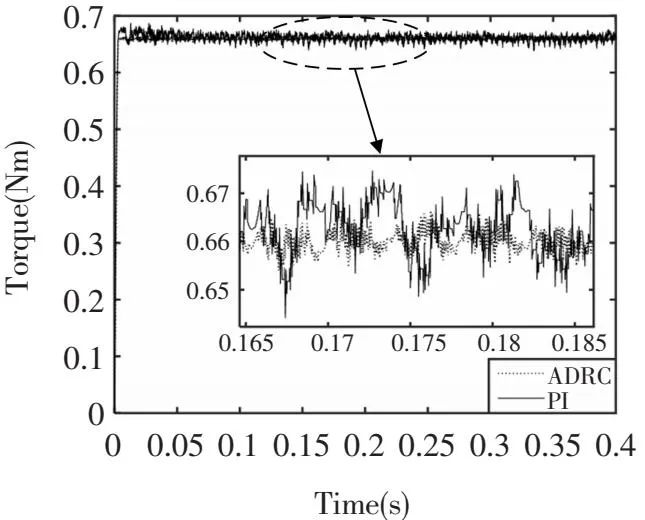
圖7 ADRC_DTC和傳統PI_DTC磁鏈仿真圖

從圖7中的波形放大部分可以看出,ADRC_DTC策略磁鏈的波動范圍值為0.664 Wb到0.654 Wb之間,波動大小為0.01 Wb。從圖7中的波形放大部分,可以看出PI_DTC策略的磁鏈波動范圍是0.671 Wb到0.639 Wb之間,波動大小為0.032 Wb。

圖8為上述控制策略的轉矩實驗波形,圖8(a)為ADRC_DTC策略的磁鏈實驗波形,圖8(b)為PI_DTC策略的磁鏈實驗波形。從這兩種策略的實驗波形中可以看出,磁鏈的響應仿真結果吻合。

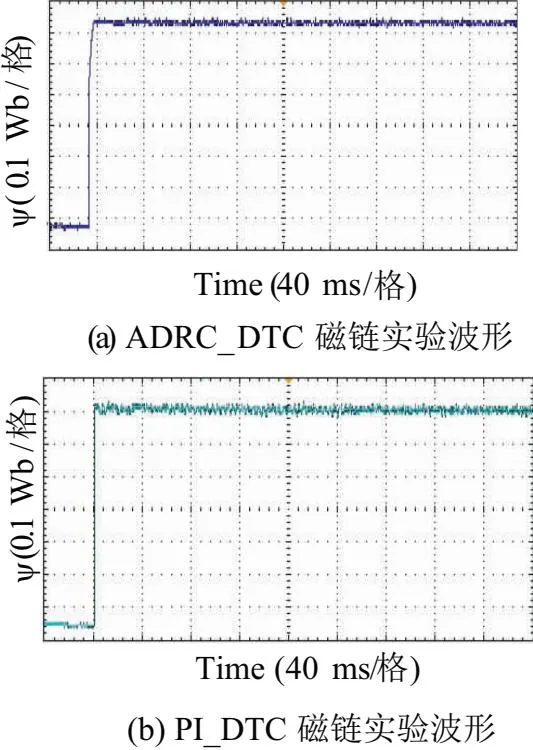
圖8 ADRC_DTC策略和傳統PI_DTC策略磁鏈實驗波形圖

4 結束語

針對傳統PI_DTC策略中轉矩脈動大和磁鏈脈動大、轉速超調等缺點,提出了一種基于自抗擾控制器的直接轉矩控制方法。通過搭建半實物仿真平臺驗證了所提出的控制策略的可行性和有效性,并且得出以下結論：

1)針對PI控制器不能滿足永磁同步電機控制過程中的非線性要求,將PI控制器全部替換為非線性的自抗擾控制器;

2)ADRC_DTC策略降低了控制過程中轉矩和磁鏈的脈動。相對與傳統PI_DTC,提出的控制方法轉矩脈動減少了70.59%,磁鏈脈動減少了68.75%,證明了所提出方法的優越性;

3)ADRC_DTC策略完全沒有超調量,可以平穩且快速地跟蹤上參考轉速。傳統的PI_DTC策略中的轉速超調到達730 r/min,所提出的控制策略對于其超調量有了極大的改善。