一類仙人掌圖的D(2)-點(diǎn)可區(qū)別全染色

汪銀芳, 李沐春, 王國興

(1. 蘭州交通大學(xué) 應(yīng)用數(shù)學(xué)研究所, 蘭州 730070; 2. 蘭州財(cái)經(jīng)大學(xué) 信息工程學(xué)院, 蘭州 730020)

0 引 言

本文所考慮的圖均為簡單無向連通圖. 設(shè)G=(V,E)是一個(gè)圖, 其中V(G)表示圖G的頂點(diǎn)集,E(G)表示圖G的邊集.對(duì)?v∈V(G), 記d(u)為頂點(diǎn)v的度,Δ(G)=max{d(u)|u∈V(G)}稱為點(diǎn)u的最大度.特別地, 當(dāng)d(u)=1時(shí), 點(diǎn)u稱為圖G的懸掛點(diǎn), 與u關(guān)聯(lián)的邊稱為懸掛邊.設(shè)d(u,v)=min{d(u,v)|u,v∈V(G)}為圖G中點(diǎn)u到點(diǎn)v的距離.若G可以分解成恰好有一個(gè)公共頂點(diǎn)v的兩個(gè)非空子圖G1和G2, 則點(diǎn)v稱為圖G的分離點(diǎn).不包含分離點(diǎn)的連通圖稱為塊.仙人掌圖[1]是一個(gè)每個(gè)塊均為圈或邊的連通圖, 簡記為GT.圈圖Cp(p≥3)的每個(gè)點(diǎn)添加一條懸掛邊所得到的圖稱為太陽圖, 記作Sn, 顯然n=2p.設(shè)仙人掌圖G的每個(gè)塊所構(gòu)成的集合為B={B1,B2,…,Bm}, 分離點(diǎn)所構(gòu)成的集合為X={u1,u2,…,un}, 每個(gè)塊收縮成點(diǎn)所構(gòu)成的頂點(diǎn)集為Y={y1,y2,…,ym}.以X和Y構(gòu)造二部圖B(G)=(X,Y), 對(duì)任意的1≤i≤n, 1≤j≤m,ui與yj相鄰當(dāng)且僅當(dāng)分離點(diǎn)ui與塊Bj關(guān)聯(lián), 此時(shí)B(G)稱為圖G的塊樹[2].此外, 塊樹中度為1的頂點(diǎn)對(duì)應(yīng)原圖中的塊稱為端塊[2].如圖1所示, 仙人掌圖GT的分離點(diǎn)為{u1,u2,u3}, 組成仙人掌圖GT的塊為{B1,B2,B3,B4,B5}, 每個(gè)塊對(duì)應(yīng)收縮成的點(diǎn)集為{y1,y2,y3,y4,y5}, 構(gòu)成了塊樹B(GT).

圖1 仙人掌圖GT及其對(duì)應(yīng)的塊樹B(GT)Fig.1 Cactus graph GT and its corresponding block tree B(GT)

目前, 關(guān)于圖染色問題的研究已有很多結(jié)果.例如: Burris[3]首次提出了圖的點(diǎn)可區(qū)別邊染色; Zhang等[4]在點(diǎn)可區(qū)別邊染色的概念上, 通過限制頂點(diǎn)的距離提出了圖鄰點(diǎn)可區(qū)別邊染色的概念, 即對(duì)于一個(gè)正常邊染色滿足相鄰點(diǎn)的色集合不相同時(shí)稱為圖的鄰點(diǎn)可區(qū)別邊染色(也稱為圖的鄰強(qiáng)邊染色); 張忠輔等[5]在正常全染色的基礎(chǔ)上, 提出了D(β)-點(diǎn)可區(qū)別全染色, 并給出了路、 圈、 完全圖以及一些聯(lián)圖等的D(2)-點(diǎn)可區(qū)別全色數(shù).下面給出圖的D(β)-點(diǎn)可區(qū)別全染色的概念.

定義1[5]若圖G的一個(gè)正常k-全染色f滿足?u,v∈V且1≤d(u,v)≤β時(shí)均有C(u)≠C(v), 則f稱為G的一個(gè)k-D(β)-點(diǎn)可區(qū)別全染色(簡記為k-D(β)-VDTC), 其中C(u)={f(u)}∪{f(uv)|uv∈E(G)}.將圖G進(jìn)行D(β)-點(diǎn)可區(qū)別全染色所需顏色的最小值稱為G的D(β)-點(diǎn)可區(qū)別全色數(shù), 簡記為χβvt(G).顯然χβvt(G)=min{k|G具有一個(gè)k-D(β)-點(diǎn)可區(qū)別全染色}.

特別地, 當(dāng)β=2時(shí),D(β)-點(diǎn)可區(qū)別全染色稱為D(2)-點(diǎn)可區(qū)別全染色.

猜想1[4-5]對(duì)于階至少為2的連通圖G, 有χ2vt(G)≤μ2(G)+1, 其中μG為圖G的2-距離以內(nèi)的組合全度.

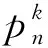
1 預(yù)備知識(shí)

引理1[5]設(shè)Pn(n≥3)是n階的路, 則

引理2[5]設(shè)圖Cn是階數(shù)為n(n≥3)的圈, 則有

引理3[5]對(duì)于圖G, 有χ2vt(G)≥Δ+1; 若G中存在距離不超過2的兩個(gè)最大度點(diǎn), 則χ2vt(G)≥Δ+2.

設(shè)f是圖G的一個(gè)正常k-全染色, 對(duì)?u,v∈V(G), 如果C(u)≠C(v), 則稱u和v在f下是可區(qū)別的.顯然如下命題成立.

命題1設(shè)f是圖G的一個(gè)正常k-全染色, 若d(u)≠d(v), 則u和v在f下是可區(qū)別的.

引理4設(shè)圖Sn(n≥3)是太陽圖, 則χ2vt(Sn)=5.

證明: 設(shè)Cg=v1v2…vgv1(g≥3)為太陽圖Sn的基本圈, 圈上每個(gè)點(diǎn)vi關(guān)聯(lián)的懸掛邊為vixi, 其中懸掛點(diǎn)為xi(1≤i≤g).由引理3可知χ2vt(Sn)≥5.下證Sn有一個(gè)5-D(2)-VDTC.令f為V(Sn)∪E(Sn)→{1,2,3,4,5}的一個(gè)映射.

當(dāng)g=3,4,5時(shí), 其染色方案如圖2所示.

圖2 太陽圖的圈長為3,4,5的D(2)-點(diǎn)可區(qū)別全染色Fig.2 D(2)-VDTC of solar graph with cycle lengths of 3,4,5

當(dāng)g≥6時(shí), 分以下4種情形討論:

情形1) 當(dāng)g≡0(mod 4)時(shí), 染色方案如下: 對(duì)于Cg的點(diǎn)vk和邊vkvk+1, 若k≡1(mod 4), 則令f(vk)=1,f(vkvk+1)=4; 若k≡2(mod 4), 則令f(vk)=2,f(vkvk+1)=1; 若k≡3(mod 4), 則令f(vk)=3,f(vkvk+1)=2; 若k≡0(mod 4), 則令f(vk)=4,f(vkvk+1)=3; 對(duì)于懸掛邊和懸掛點(diǎn), 設(shè)f(vixi)=5,f(xi)=f(vivi+1), 其中1≤i,k≤g.

情形2) 當(dāng)g≡1(mod 4)時(shí), 染色方案如下: 對(duì)于Cg的點(diǎn)vk和邊vkvk+1, 若k≡1(mod 4), 則令f(vk)=1,f(vkvk+1)=4; 若k≡2(mod 4), 則令f(vk)=2,f(vkvk+1)=1; 若k≡3(mod 4), 則令f(vk)=3,f(vkvk+1)=2; 若k≡0(mod 4), 則令f(vk)=4,f(vkvk+1)=3.其中1≤k≤g-5.而f(vg-4)=1,f(vg-3)=2,f(vg-2)=4,f(vg-1)=1,f(vg)=4;f(vg-4vg-3)=4,f(vg-3vg-2)=1,f(vg-2vg-1)=3,f(vg-1vg)=2,f(vgv1)=3.對(duì)于懸掛邊和懸掛點(diǎn),f(vg-2xg-2)=2,f(vixi)=5(i≠g-2);f(xi)=f(vivi+1), 其中1≤i≤g.

情形3) 當(dāng)g≡2(mod 4)時(shí), 染色方案如下: 對(duì)于Cg的點(diǎn)vk和邊vkvk+1, 若k≡1(mod 4), 則令f(vk)=1,f(vkvk+1)=4; 若k≡2(mod 4), 則令f(vk)=2,f(vkvk+1)=1; 若k≡3(mod 4), 則令f(vk)=3,f(vkvk+1)=2; 若k≡0(mod 4), 則令f(vk)=4,f(vkvk+1)=3.其中1≤k≤g-2.而f(vg-1)=2,f(vg)=5,f(vg-2vg-1)=1,f(vg-1vg)=3.對(duì)于懸掛邊和懸掛點(diǎn), 當(dāng)1≤i≤g-2時(shí),f(vixi)=5,f(vg-1xg-1)=4,f(vgxg)=2;f(xi)=f(vivi+1)(1≤i≤g).

情形4) 當(dāng)g≡3(mod 4)時(shí), 染色方案如下: 對(duì)于Cg的點(diǎn)vk和邊vkvk+1, 若k≡1(mod 4), 則令f(vk)=1,f(vkvk+1)=4; 若k≡2(mod 4), 則令f(vk)=2,f(vkvk+1)=1; 若k≡3(mod 4), 則令f(vk)=3,f(vkvk+1)=2; 若k≡0(mod 4), 則令f(vk)=4,f(vkvk+1)=3.其中1≤k≤g-3.而f(vg-2)=1,f(vg-1)=3,f(vg)=4,f(vg-2vg-1)=4,f(vg-1vg)=2,f(vgv1)=3.對(duì)于懸掛邊和懸掛點(diǎn),f(vg-1xg-1)=1,f(vixi)=5(i≠g-1);f(xi)=f(vivi+1)(1≤i≤g).

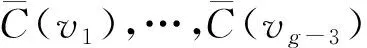
綜上,χ2vt(Sn)=5, 結(jié)論成立.

注1在引理4的證明中, 至少存在一個(gè)懸掛點(diǎn)與它鄰點(diǎn)在圈上的某條關(guān)聯(lián)邊染同色; 染色函數(shù)f是Sn的基本圈Cg的一個(gè)5-D(2)-VDTC.

p階圈圖Cp(p≥3)的點(diǎn)上任意添加懸掛邊所得到的圖稱為破太陽圖.特別地,Cp的每個(gè)點(diǎn)上都添加懸掛邊即為太陽圖.記破太陽圖的基本圈為Cp=v1v2…vpv1(p≥3), 圈圖的部分點(diǎn)上添加的懸掛邊為vixi, 其中懸掛點(diǎn)記為xi,i∈{1,2,…,p}.

引理5設(shè)圖G是一個(gè)破太陽圖, 則有χ2vt(G)≤5.

證明: 設(shè)G*是G添加懸掛邊后得到的太陽圖, 顯然,G是G*的一個(gè)子圖.由引理4可知,G*存在一個(gè)5-D(2)-VDTCf, 同時(shí)也是G*的基本圈的一個(gè)5-D(2)-VDTC.因此,f|G為G的一個(gè)5-D(2)-VDTC.

2 主要結(jié)果

定理1設(shè)GT為最大度為3的仙人掌圖, 則χ2vt(GT)≤6.

證明: 對(duì)仙人掌圖GT的塊數(shù)t進(jìn)行歸納.

顯然t≥2(由于t=1不存在最大度為3的仙人掌圖).當(dāng)t=2時(shí), 僅有圈上關(guān)聯(lián)一條懸掛邊的圖滿足最大度為3, 不妨記該仙人掌圖GT上的圈為Cn=u1u2…unu1, 懸掛邊為u1x1, 其中u1是GT的分離點(diǎn).先給圈Cn著色, 由引理2知, 圈Cn存在一個(gè)5-D(2)-VDTCf′, 再從集合{1,2,3,4,5}{f′(u1),f′(u1u2),f′(u1un)}中任選一種顏色染給邊u1x1, 令點(diǎn)x1與邊u1u2染同色, 從而得到圖GT的一個(gè)著色方案f.在f中, 圈上的2度點(diǎn)均為D(2)-點(diǎn)可區(qū)別的.注意到d(x1)≠d(ui), 其中i=1,2,…,n.由命題1知點(diǎn)x1和點(diǎn)u1與2-距離以內(nèi)所有點(diǎn)的色集合不同, 因此f是圖GT的一個(gè)5-D(2)-VDTC.

假設(shè)結(jié)論對(duì)塊數(shù)小于t的仙人掌圖GT都成立.下面考慮GT中t≥3的情形, 設(shè)GT的塊樹中最長路為P, 對(duì)路P的端點(diǎn)對(duì)應(yīng)GT中的端塊是邊或者是圈, 分以下兩種情形討論.

情形1) 存在一條路P的某個(gè)端點(diǎn)對(duì)應(yīng)GT中的端塊是邊.

設(shè)該邊為uv, 其中u為分離點(diǎn), 由歸納假設(shè)知GT-uv存在一個(gè)6-D(2)-VDTCf′, 在f′的基礎(chǔ)上給邊uv及點(diǎn)v進(jìn)行染色, 將f′延拓為圖GT的一個(gè)6-D(2)-VDTCf.對(duì)點(diǎn)u的除v外的任意一個(gè)鄰點(diǎn)x, 再分兩種情形討論.

① 點(diǎn)x不屬于路P的某個(gè)端點(diǎn)對(duì)應(yīng)GT中的塊.

u除v外至多有兩個(gè)鄰點(diǎn), 不妨設(shè)為點(diǎn)x1和x2(如果存在), 其中x1屬于路P中某個(gè)端點(diǎn)對(duì)應(yīng)GT中的塊,x2不屬于路P中某個(gè)端點(diǎn)所對(duì)應(yīng)GT中的塊, 且點(diǎn)x2不能再關(guān)聯(lián)其他塊, 否則與邊uv屬于路P最后一個(gè)端點(diǎn)對(duì)應(yīng)GT中的塊矛盾, 如圖3所示.記x1除u外的其他鄰點(diǎn)為點(diǎn)y1和y2(如果存在).若給點(diǎn)u重染色不改變x1和x2的色集合, 則可以給u重染色.因?yàn)閒(u)≠f(ux1),f(u)≠f(x1),f(u)≠f(ux2),f(u)≠f(x2), 故點(diǎn)u可用色至少有6-4=2種; 因?yàn)閒(uv)≠f(u),f(uv)≠f(ux),f(uv)≠f(ux1), 故邊uv的可用色至少有6-3=3種.從而u至少有2×3=6種可用色集合.為區(qū)分u的色集合與至多3個(gè)同度點(diǎn)x1,y1,y2的色集合, 可從u的至少6種可用色集合中除去可能與x1,y1,y2的色集合相同的至多3種, 從余下至少3種色集合中任選一種分配給點(diǎn)u及邊uv.因?yàn)閐(u)≠d(x2),d(u)≠d(v), 故由命題1知u的色集合與點(diǎn)v,x2的色集合可區(qū)別.又因?yàn)閒(v)≠f(uv),f(v)≠f(u), 故點(diǎn)v的可用色有6-2=4種,d(v)=d(x2)=1, 從v的可用色集合中除去可能與x2的色集合相同的那種, 再從余下的至少3種可用色集合中任選一種分配給點(diǎn)v, 則點(diǎn)v與2-距離的同度點(diǎn)x2的色集合可區(qū)別, 于是有χ2vt(GT)≤6.

圖3 x2不屬于最長路Fig.3 x2 does not belong to the longest path

② 點(diǎn)x屬于路P中某個(gè)端點(diǎn)對(duì)應(yīng)GT中的塊.

此時(shí), 與點(diǎn)u相鄰的點(diǎn)x至多有2個(gè).

(i)x的個(gè)數(shù)為1.

此時(shí), 根據(jù)d(u)=2或3, 以及d(x)=2或3分3種情形, 其中點(diǎn)u在2-距離內(nèi)至多有2個(gè)同度點(diǎn), 如圖4所示.由于f(uv)≠f(u),f(uv)≠f(ux), 所以邊uv可用色有6-2=4種, 從uv的4種可用色中除去使得點(diǎn)u與至多2個(gè)同度點(diǎn)色集合相同的那2種色, 再從剩下的至少2種可用色中任選一種分配給邊uv, 再從集合{1,2,3,4,5,6}{f(uv),f(u)}中任選一種染給點(diǎn)v.d(v)≠d(u),d(v)≠d(x), 由命題1知點(diǎn)v與2-距離內(nèi)的點(diǎn)的色集合都不同.

圖4 x∈P且有1個(gè)xFig.4 x∈P and has one x

(ii)x的個(gè)數(shù)為2, 如圖5所示.

圖5 x∈P且有2個(gè)xFig.5 x∈P and has two x

此時(shí)d(u)=3,u的除v外的2個(gè)鄰點(diǎn)記為x1,x2, 記點(diǎn)x1,x2在圈上除點(diǎn)u外的鄰點(diǎn)為y1,y2.點(diǎn)x1,x2,y1,y2可以關(guān)聯(lián)其他的塊, 但是都至多只能關(guān)聯(lián)一個(gè)塊, 否則uv所在塊樹的路就不是最長路; 且點(diǎn)x1,x2,y1,y2關(guān)聯(lián)的塊只能是邊, 否則Δ>3.

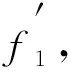
為證明GT是6色可染的, 只需驗(yàn)證G1和G2在上述染色方案不變的前提下粘合邊w3w后仍滿足2-距離之內(nèi)的點(diǎn)的色集合不同即可.記構(gòu)造得到的GT全染色為

(1)

情形2) 任意一條路P的某個(gè)端點(diǎn)對(duì)應(yīng)GT中的端塊是圈.

如圖6所示, 由于Δ=3, 故與最后一個(gè)圈關(guān)聯(lián)的塊只能為邊.設(shè)u1為塊樹中某一條最長路的最后一個(gè)分離點(diǎn),Cm=u1u2…umu1(m≥3)是GT的塊樹中最長路的某端點(diǎn)對(duì)應(yīng)的端塊, 點(diǎn)u1的除u2和um的鄰點(diǎn)記為y, 點(diǎn)y除鄰點(diǎn)u1外, 至多還有2個(gè)鄰點(diǎn)不妨設(shè)為y1和y2.

圖6 最后一個(gè)塊為圈Fig.6 The last block is cycle

為證明GT是6色可染的, 只需驗(yàn)證G1和G2在上述染色方案不變的前提下粘合邊zw后仍滿足2-距離之內(nèi)的點(diǎn)的色集合不同即可.記構(gòu)造得到的GT的全染色為式(1).