網絡攻擊下電力系統的離散遲滯量化控制

謝佳杰, 宋公飛, 杜 鵬

(1.南京信息工程大學 自動化學院,江蘇 南京 210044; 2.南京信息工程大學 江蘇省大氣環境與裝備技術協同創新中心,江蘇 南京 210044)

量化控制作為控制工程領域的前沿熱點問題,受到廣大科研工作者的關注。在網絡控制的應用中,系統設備之間的信息通過通信網絡在離散時間使用數據包傳輸,這個過程通常占用大量的網絡資源,例如網絡帶寬、計算能力等[1]。因此量化控制在網絡控制中扮演著舉足輕重的角色,其作用是通過量化器將接收到的連續信號近似為有限多個離散值,從而減少控制器接收信號所包含的信息,但是又不使輸入信號失真[2]。因此將量化控制應用于網絡系統的想法順其自然地產生了。然而隨著網絡化系統的應用與發展,單獨的量化控制并不能完全滿足信息傳輸的要求,因此,考慮在量化控制的基礎上對系統進行離散化處理,進一步減少網絡系統中傳輸信號所包含的非必要信息,從而降低網絡通信壓力。

近年來網絡系統抵抗網絡攻擊的能力,即網絡系統的穩定性成為研究的熱點[3]。為了使系統穩定并且盡可能降低網絡通信壓力,許多學者選擇設計量化反饋控制器,取得了很多有意義的成果。例如文獻[4]研究了當網絡系統遭到欺騙攻擊時系統的預測控制并且給出了系統穩定的條件。文獻[5]研究了隨機非線性系統在遭到網絡欺騙攻擊時基于離散觀測的安全控制問題,建立了矩陣不等式形式的充分條件,保證了預先確定的概率安全性。文獻[6]提出了一種對數量化反饋控制器的幾何設計方法,此方法適用于處理一類非線性系統。文獻[7]在網絡系統中應用對數量化器對傳輸信號進行量化并且考慮了系統受到網絡欺騙攻擊時是否能夠保證穩定的問題。對數量化器易產生抖震現象,不利于系統的穩定,因此文獻[7]給出了一個新的遲滯量化器,利用自適應控制反步法研究一類具有量化輸入的非線性不確定系統。文獻[8]同樣運用反步法設計了控制器,但是其提出文獻[7]設計的穩定條件具有特殊性。因此,為了解決這一問題,文獻[9]針對具有遲滯量化輸入的嚴格反饋系統,研究了一種基于反推的自適應穩定方法。但是文獻[7]和文獻[8]都是基于不確定的非線性是已知函數,其參數未知并且對于這些已知函數是線性的,同時非線性函數滿足全局Lipschitz條件。文獻[10]和文獻[11]提出了一種具有量化輸入信號的隨機嚴格反饋非線性系統的模糊自適應方法,文獻[11]同時考慮了不確定非線性和未知的隨機擾動,并且對量化輸入提出一種新的非線性分解,建立了控制信號與量化信號之間的關系。隨著對遲滯量化器的深入研究,在網絡控制以及非線性自適應控制方面取得了顯著進步,其中利用反步控制算法設計自適應控制器的策略更是成為解決非線性系統控制問題的一個突出方向[11-13]。此外,文獻[14]研究了受多面體類型不確定性影響的離散時間馬爾可夫鏈驅動的系統和受時滯影響的非線性隨機系統,同時提出了線性矩陣不等式理論來設計反饋控制器。文獻[15]提出了基于離散狀態和模式觀測的混合隨機系統加以魯棒量化控制的方法,從而減少網絡通信的負擔,降低信號傳輸的丟包率。結合以上文獻,在網絡混雜隨機系統中,采用基于狀態和模態離散觀測的遲滯量化反饋控制,能夠進一步提高網絡通信效率并保證系統的穩定性。

由于電力系統十分重要并且具有實際意義,因此針對電力系統研究出了許多控制方法。例如文獻[16]針對艦船綜合電力系統,利用改進蝙蝠算法優化控制器的模糊規則,加快自適應控制速度。文獻[17] 設計了一種基于邏輯開關控制的切換控制器并從理論上證明了切換控制器與被控系統組成的閉環系統的穩定性。以上控制并不能有效解決網絡通信過程中數據過多的問題,因此,本文設計的離散遲滯量化器能夠降低網絡通信壓力。

本文的主要創新點如下:

① 在網絡系統中首次采用遲滯量化反饋控制,建立了網絡欺騙攻擊下隨機網絡系統的數學模型,其中發生與未發生網絡欺騙攻擊的數學模型通過伯努利隨機變量組合在一起。

② 將遲滯量化反饋控制器應用于離散觀測系統中,進一步降低了控制成本,節約了通信資源,并且通過應用遲滯量化器,消除了對數量化器帶來的抖震現象。

③ 將離散觀測應用于網絡系統中,減少了網絡節點接收的信號,同時又保證接收到的信號不失真,從而提高了網絡資源的利用率、減輕了網絡信號傳輸時的通信壓力。

1 系統描述及預備知識

1.1 系統描述

考慮如下具有不確定結構的電力系統隨機網絡控制模型:

dx(t)=[(A(r(t))+ΔA(t,r(t)))x(t)+u(x([t/τ]τ),

r([t/τ]τ))+C(r(t))g(x(t),r(t))]dt+

(1)

式中:x(t)為狀態變量;r(t),t≥0為概率空間上的右連續馬爾可夫鏈,取有限狀態空間S={1,2,…,N}中的值;ω(t)=[ω1(t)ω2(t) …ωn(t)]為m維布朗運動;u(x([t/τ]τ),r([t/τ]τ))為控制輸入,控制輸入以如下形式表現:

u(x([t/τ]τ),r([t/τ]τ))=
E(r(t))qr(t)(K(r([t/τ]τ))x([t/τ]τ))

式中:E(·),K(·)為給定的具有適當維數的參數矩陣;qr(t)為模態相關的遲滯量化器;生成元Γ=(γij)N×N由下式得:

ΔA(t,i)=LaFa(t)NAi, ΔBk(t,i)=LbFb(t)NBki

(2)

式中:La,Lb,NAi,NBki為已知實常數矩陣并且Fa(t),Fb(t):R+→Rs×t為實值時變矩陣滿足:

Fa(t)TFa(t)≤I,Fb(t)TFb(t)≤I

(3)

式中:I為單位矩陣。

通過文獻[1]的啟示,考慮網絡攻擊模型為

(4)

式中:φ(t)=[t/τ]τ,[t/τ]τ是t/τ的整數部分;0≤ψ(t)≤1是隨機分布的伯努利變量;fi(x(φ(t)))為網絡欺騙攻擊信號,滿足[18]:

‖fi(x(t))‖≤‖Yx(t)‖

(5)

式中:Y為一個已知正定矩陣。

因此,可以得到控制輸入為

(6)

系統中的g(x(t),r(t))gi(x(t)):Rn×S→Rn為可微非線性函數,并有如下假設。

假設1[18]:假設gi(x(t))是關于x(t)的全局Lipschitz函數,如果|gi(0)|=0并且:

|gi(x1(t))-gi(x2(t))|≤ζ|x1(t)-x2(t)|

(7)

式中:ζ>0稱為Lipschitz條件,則具有離散控制器的系統(1)可以表示為

dx(t)=[(A(r(t))+ΔA(t,r(t)))x(t)+

E(r(t))qr(t)(K(r([t/τ]τ))×

(ψ(t)fi(x(φ(t)))+(1-ψ(t))x(φ(t))))+

ΔBk(t,r(t))]x(t)dωk(t)

(8)

式中[19]:

(9)

(10)

式中:Di、Mi、Tgi、Tchi、σi、Ri分別為區域i內的阻尼系數、慣性常數、調速器的時間常數、渦輪常數、頻率偏置常數、跌落特性。

1.2 遲滯量化器

本文中采用遲滯量化器來避免抖震現象。抖震是一種高頻振蕩,在對數量化器中,假設控制信號u在量化邊沿Q附近發生振蕩(以先減小后增大再減小為例),如圖1所示,q(u)將在量化級別RM和PQ之間高頻振蕩,即R→Q→R,從而引發了抖振現象。

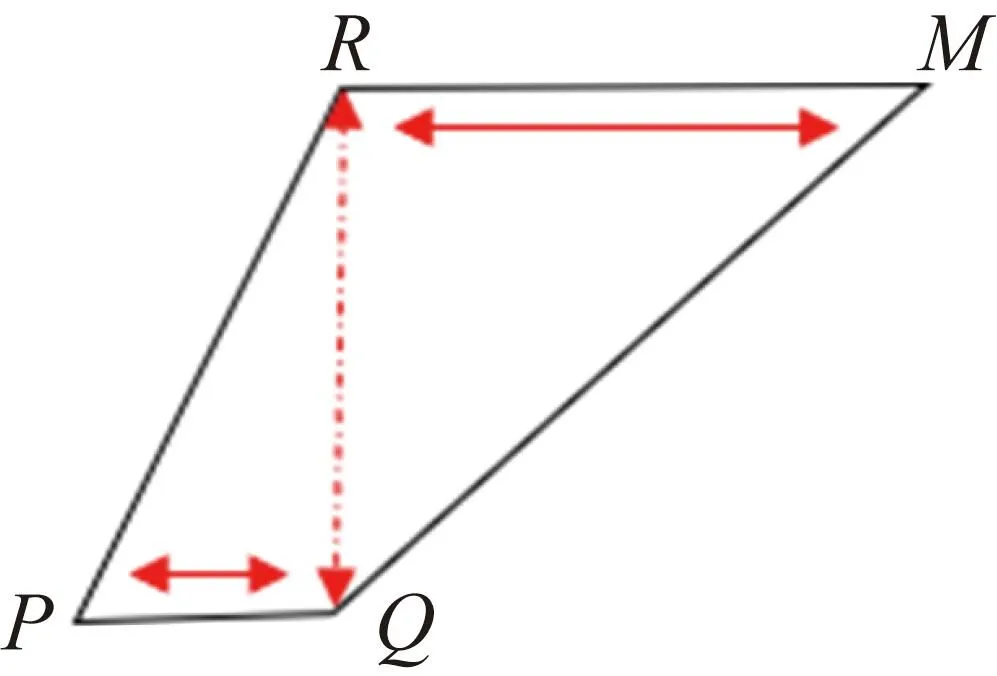
圖1 對數量化局部曲線

為了避免抖振現象,采用遲滯量化器的量化方法。遲滯量化器采用2個量化密度相同但量化值不同的量化器,分別為量化器1和量化器2。同一時間只有一個量化器在工作,當量化器切換時,量化值變化。

在遲滯量化器中,假設控制信號u在量化邊沿R附近發生振蕩(以先減小后增大再減小為例),如圖2所示,開始時量化信號q(u)位于量化器1的量化級別RM的Rc上,當u減小到小于量化邊沿R時,q(u)從量化器1的量化級別RM上切換到量化器2的量化級別NJ并處在Nb上;當u增大時,q(u)從量化器2的量化級別NJ切換到量化器1的量化級別PQ并處在aQ上;當u增大到大于量化邊沿Q時,q(u)從量化器1的量化級別PQ切換到量化器2的量化級別NJ并處在bJ上;當u再次減小時,q(u)從量化器2的量化級別NJ切換到量化器1的量化級別RM并處在Rc上,回到量化邊沿R處。整個過程即Rc→Nb→aQ→bJ→Rc。

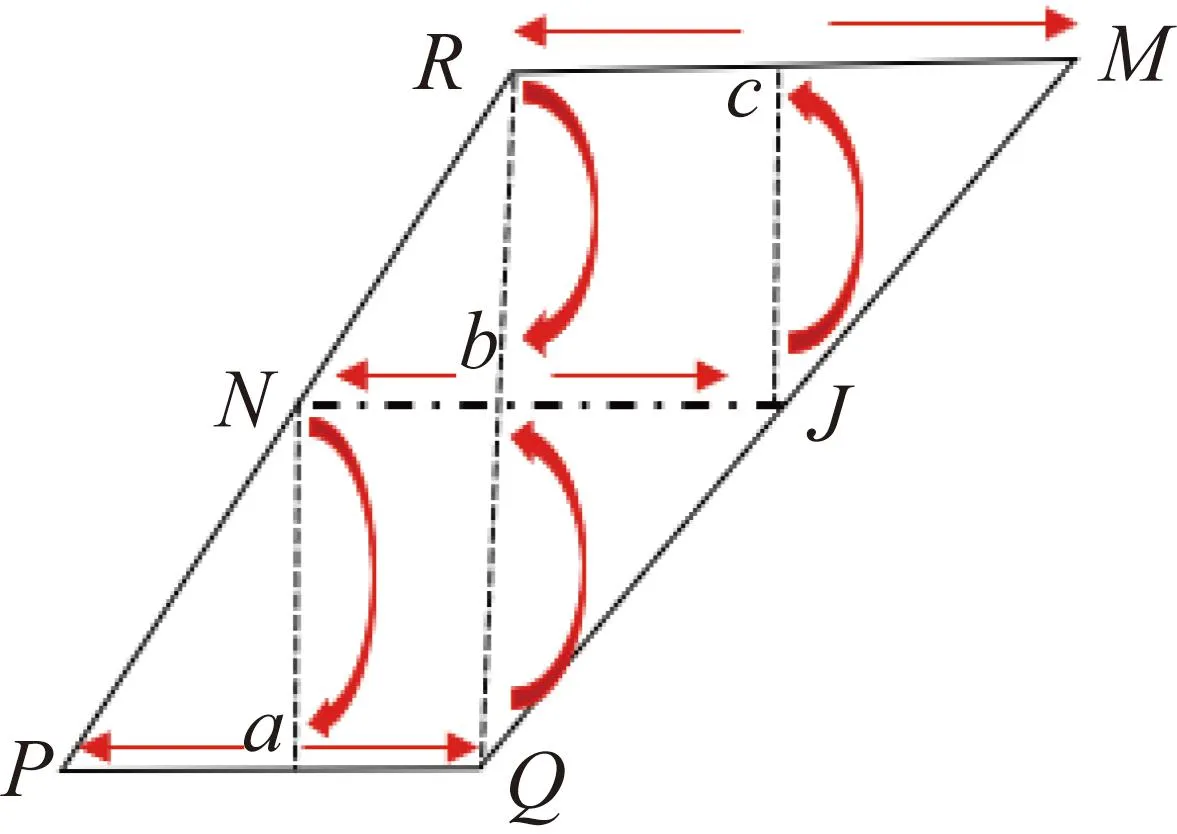
圖2 遲滯量化局部曲線

對比對數量化器和遲滯量化器在u發生振蕩時,對數量化器的量化值是2個值直接變化,而遲滯量化器的量化值歷經多個值的變化,這種變化為量化值q(u)的變化提供了停留時間,可以看作是為量化器添加滯后的方法,避免了抖振現象。

遲滯量化器在文獻[20]中被首次提出。模態相關的遲滯量化器形式如下:

(11)

量化器qi(u(t))以類似于文獻[8]和文獻[21]的形式表示遲滯量化器:

(12)

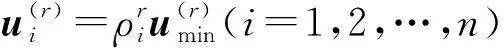
引理1[22]:為了達到應用遲滯量化器控制的目的,將遲滯量化器分為線性部分與非線性部分,表達形式如下:

q(u)=u(t)+D(t)

(13)

式中:D(t)=qi(u(t))-u(t)∈?1。

非線性部分D(t)滿足以下不等式:

(14)

(15)

2 控制器設計

在繼續推導之前,給出如下引理,這些引理將用于證明系統(1)是均方指數穩定的。

引理2[15]:對任意的t≥0,v>0和i∈S,滿足:

(16)

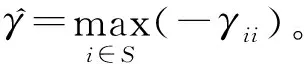
引理3:設x(t)為系統(1)的解。

并且定義:

h(τ)=(8τ2Ma+8τ2ζ2+8τMb+4τ2Y2MK)×

e8τ2Ma+8τ2ζ2+8τMb,τ>0

(17)

H(τ)=(8τ2Ma+8τ2ζ2+8τMb+4τ2MK)×

e8τ2Ma+8τ2ζ2+8τMb,τ>0

(18)

F(τ)=64τ2Mu(τ2Ma+τ2ζ2+τMb)

e8τ2Ma+8τ2ζ2+8τMb,τ>0

(19)

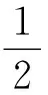
(20)

(21)

(22)

下文繼續討論基于離散時間狀態和模式觀測的遲滯量化反饋控制器位于控制器到執行器側時,系統(1)的穩定性問題。

定理1:當發生網絡攻擊時,假設存在矩陣Ki>0、Qi>0以及正定標量βi,ε,ζ,β2i,ηi(i∈s)使下列式子

(23)

如果τ足夠小,滿足:

(24)

那么系統(1)滿足:當u(s)≥umin,ψ(t)=1時,

(25)

即被控系統(1)在受到網絡攻擊時是均方指數穩定的。

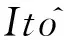
dV(x(t),r(t))=LV(x(t),r(t))dt+dM1(t)

式中:M1(t)為滿足M1(0)=0的鞅并且:

LV(x(t),i)=2x(t)TQi[(Ai+ΔAi(t))x(t)+

通過假設1可得:

2x(t)TQi[(Ai+ΔAi(t))x(t)+

2x(t)TQiEiD(t)

(26)

推論1:當系統(1)遭遇網絡攻擊并且輸入信號大于死區,即當u(s)≥umin,ψ(t)=1時,

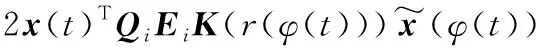
(27)

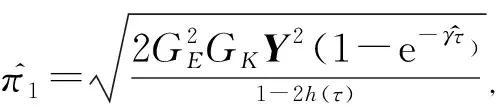
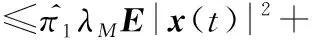
(28)

同式(27),可將2x(t)TQiEiD(t)項放縮為

(29)

(30)

通過計算可得:

我們發現，為加強與離院后病人的溝通聯系，朋友和直系親屬的姓名、地址，而非目前家庭的信息，對于保持與病人的聯系是十分有價值的。

(31)

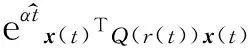
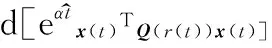
(32)

=λME|x(0)|2

(33)

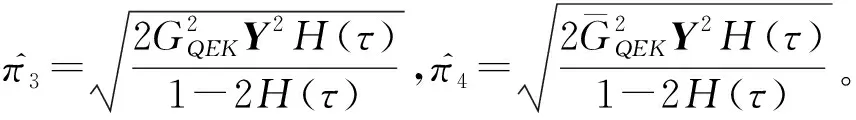
定理2:當沒有發生網絡攻擊時,假設存在矩陣Ki,Qi>0以及正定標量βi,ε,ζ,β2i,ηi(i∈s)使下列兩式:

(34)

(35)

(36)

(37)

那么系統(1)滿足:當u(s)≥umin,ψ(t)=0時,

(38)

當u(s)≤umin時,

(39)

即被控系統(1)在未受到網絡攻擊時是均方指數穩定的。

2x(t)TQiEiK(r(φ(t)))x(φ(t))
≤x(t)T(Sym{QiEiKi})x(t)+
2GQEK|x(t)|×|x(t)-x(φ(t))|-
2x(t)TQiEi(Ki-K(r(φ(t))))x(φ(t))

(40)

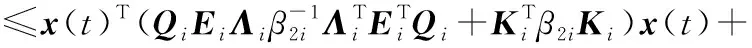
(41)

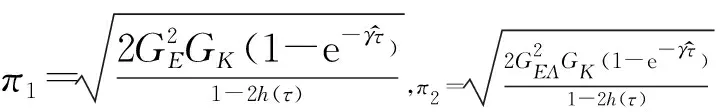
-2E[x(t)TQiEi(Ki-K(r(φ(t))))x(φ(t))]
≤2π1λME|x(t)|2

(42)

(43)

同定理1可得:

d[eαtx(t)TQ(r(t))x(t)]=eαt(αx(t)TQ(r(t))x(t)+

LV(x(t),r(t)))dt+dM3(t)

(44)

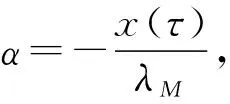
eαtE[x(t)TQ(r(t))x(t)]≤λME|x(0)|2

(45)

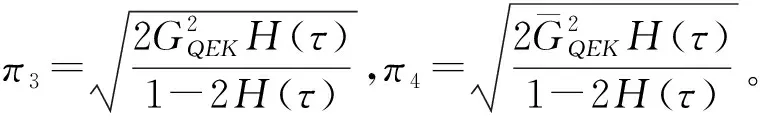
同樣的方法可以推導得出式(39)成立。因此,綜合定理1與定理2可得,被控系統(1)無論是否遭遇網絡攻擊都是均方指數穩定的。

3 仿真實驗

考慮網絡攻擊下電力系統(8)具有以下參數[24]:

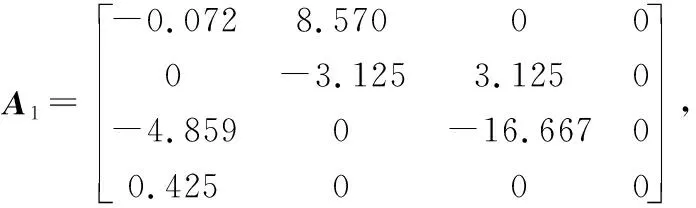
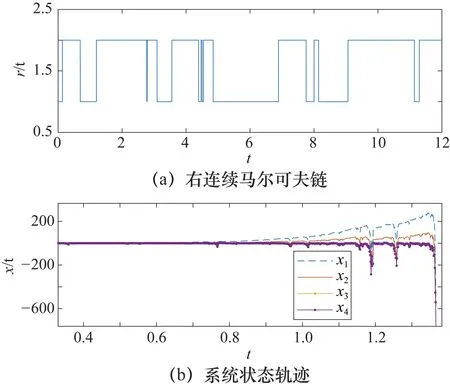
圖3 開環系統的軌跡

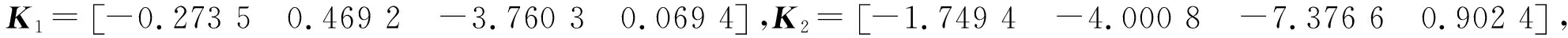
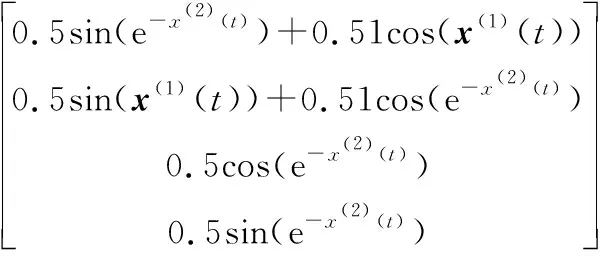
當閉環系統(1)遇到網絡欺騙攻擊時閉環系統的軌跡如圖4所示。

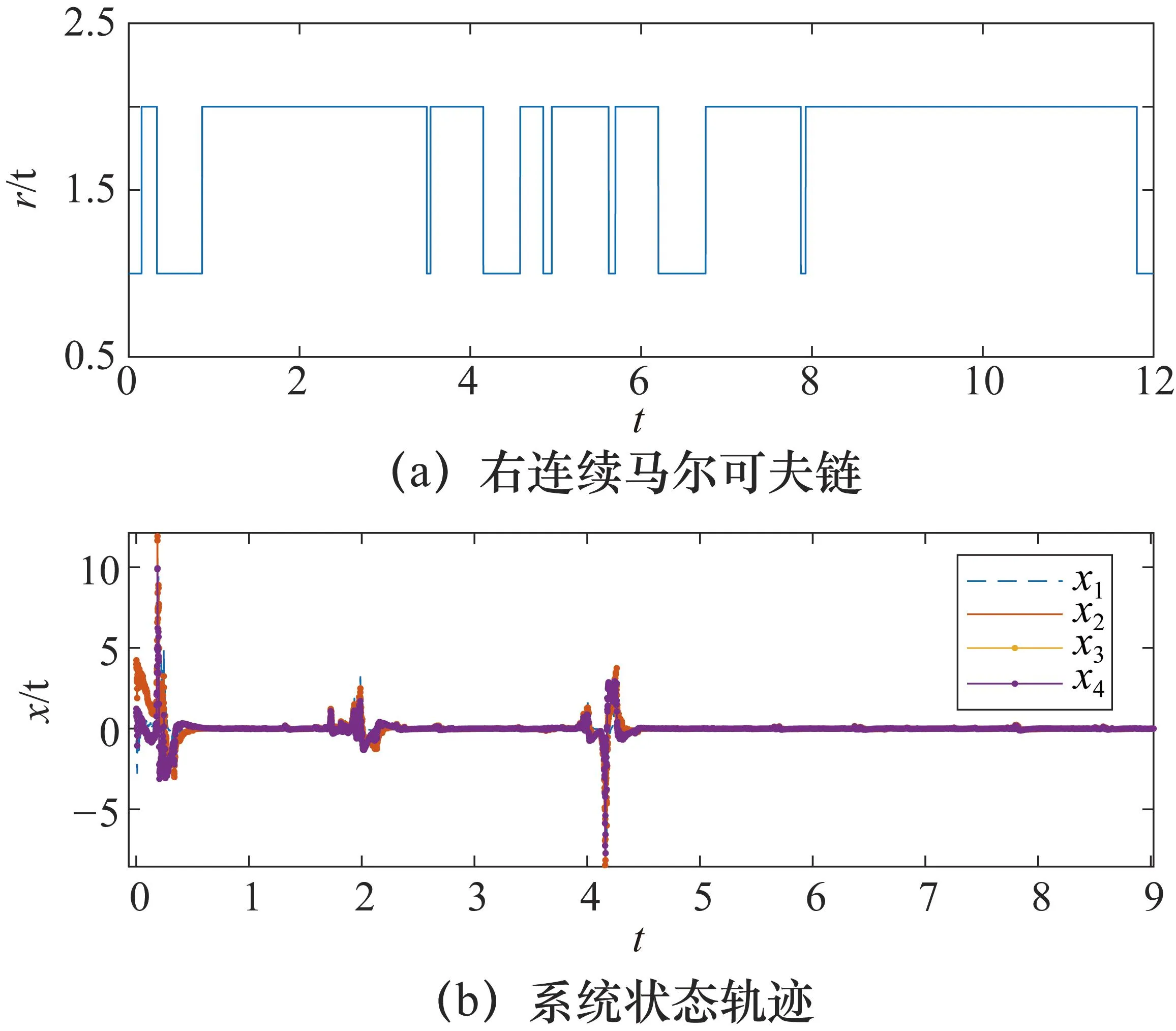
圖4 欺騙攻擊發生時閉環系統的軌跡

由圖4可以看出當網絡系統遭到網絡欺騙攻擊時,基于離散觀測狀態和模態的遲滯量化控制器仍然能夠保證隨機網絡系統的穩定性。

閉環系統(1)未受到網絡欺騙攻擊時的仿真結果如圖5所示。

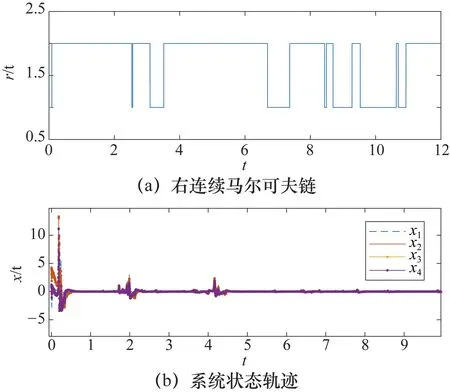
圖5 狀態反饋:閉環系統的軌跡

由圖5可以看出無網絡欺騙攻擊時,閉環系統在遭到隨機網絡波動時,仍然能夠保證系統的穩定性。

4 結束語

針對隨機網絡系統,研究了狀態和模態離散的遲滯量化反饋控制問題。設計的控制器能夠保證被控系統無論是否受到網絡欺騙攻擊都是均方指數穩定的。仿真結果也表明本文提出的控制方案是有效的。接下來的工作主要有兩個方向:首先網絡攻擊是隨機發生的,在保證無網絡攻擊時系統穩定的條件下,可以考慮將事件觸發機制加入,研究網絡攻擊下離散狀態的隨機網絡控制系統的事件觸發控制,通過該方法進一步節約隨機網絡控制資源;其次考慮網絡受到欺騙攻擊與拒絕服務攻擊時,如何增加系統的普適性。