渦扇發動機性能換算參數的溫度修正機理分析

姜繁生, 程榮輝, 賈琳淵, 張志舒, 夏 禹

(1.中國航發沈陽發動機研究所,遼寧 沈陽 110015; 2.西北工業大學 動力與能源學院,陜西 西安 710119)

渦扇發動機的性能參數隨發動機進口條件和發動機轉速變化。為了對比不同進氣條件下發動機的性能,通常根據相似原理將其性能參數換算至標況下。由無熱交換黏性可壓縮氣體的三元非定常流動的相似條件[1]可知,實現發動機工況的絕對相似是幾乎不可能的,但是可以在忽略一些次要影響因素(如雷諾數和物性參數)的條件下,使發動機近似地滿足相似條件,從而通過性能參數的相似換算便捷地將試驗數據換算至同一基準條件下。為了進一步消除被忽略的次要因素導致的相似換算參數誤差,工程上引入不同的修正系數(如雷諾數修正、濕度修正和溫度修正)對相似換算參數進行修正,從而盡可能地提高性能換算參數精度。在無特殊說明的情況下,本文所說的修正系數均指溫度修正系數。

國軍標中對發動機性能換算參數的溫度修正系數計算和驗證做出了明確的規定。GJB 378-87《渦噴渦扇發動機性能的溫度修正規范》[2]中給出了性能相似換算參數的溫度修正系數的計算方法。GJB 241A-2010《航空渦輪噴氣和渦輪風扇發動機通用規范》[3]中規定“當使用修正系數把發動機性能數據換算為標準狀態時,應在必需的環境條件范圍內進行海平面和高空試驗,以驗證性能修正系數的準確度。”

研究人員在發動機性能相似換算和溫度修正方法方面,也開展了研究和應用工作。Nyakayev[1]對N-S方程進行無量綱化處理后得到了渦輪發動機中無熱交換黏性可壓縮氣體的三元非定常流動的5個相似準則數(施特勞哈爾準則、弗勞德準則、馬赫數準則、泊松準則和雷諾準則)。廉筱純等[4]推導了發動機相似換算參數的計算公式。陳玉春等[5]介紹了發動機相似原理和組合相似參數并將其應用到渦輪發動機特性獲取的地面試車試驗中。駱廣琦等[6]介紹了發動機性能參數的換算方法和溫度修正系數的計算方法。陳大光等[7]通過對燃氣渦輪發動機在不同進氣溫度下的變比熱特性計算,分析了按相似理論導出的常規性能換算公式的誤差,并提出了較精確而實用的換算方法。賈琳淵[8]研究了相似原理在變循環發動機中的應用,并依據相似原理描述了變循環發動機節流狀態控制規律。蒲寧等[9]介紹了渦軸發動機軸功率不滿足相似原理的原因,并提出了軸功率的溫度修正方法。馬前容等[10]針對渦軸發動機高空臺試驗因素模擬偏差帶來的性能差異問題,通過某渦軸發動機數值仿真計算和試驗研究,提出了相似換算和小偏差分析相結合的試驗性能修正方法。魯峰等[11]根據試驗數據修正了相似換算參數的指數,用于提升故障診斷基線模型的精度。盧希榮等[12]利用因次分析法推導了渦扇發動機的換算參數,并以此為基礎給出了渦扇發動機飛機性能換算方法。王朝蓬等[13]通過對比高原試驗中的相似換算參數,得到了不同狀態、引氣構型和起飛方式對民用渦扇發動機性能的影響。張紅濤等[14]提出了一種考慮使用因素的渦扇發動機排氣溫度換算方法,所獲得的修正系數與試車試驗數據的相對誤差小于1.3%,有效解決了排氣溫度廠內驗收合格而外場地面開車不合格的問題。原和朋等[15]通過研究渦噴、渦扇發動機換算轉速的大氣溫度修正方法,針對航空發動機的換算轉速溫度修正偏離實際值的故障,通過大量試車試驗數據對航空發動機的換算轉速溫度修正曲線重新進行了修正,給出了較為真實的換算轉速大氣溫度修正系數。黃浩等[16]提出一種基于神經網絡的渦軸發動機性能參數換算方法,研究了相似換算公式的指數修正方法,通過修正相似換算公式的指數,提高大氣溫度和壓力影響的性能參數換算精度,在此基礎上乘以濕度修正系數以修正大氣濕度對性能參數的影響,提高了渦軸發動機性能參數換算的精度。

綜上所述,發動機性能參數的相似換算方法以及溫度修正系數的計算和驗證方法已經明確,并在學術研究和工程型號研制中廣泛應用。但是,溫度修正系數對相似換算參數的影響機理并未被闡明,亦或溫度變化時具體由哪幾個因素導致發動機不相似,以及不同因素對相似換算參數的影響量級的數值尚未被闡明。

本文以渦扇發動機變比熱性能計算程序為工具,研究不同溫度下發動機性能相似換算參數的修正系數變化情況,并定量分析不同因素對溫度修正系數的影響。

1 溫度修正系數的獲取方法

1.1 溫度修正系數的定義

發動機進口溫度為T2時,溫度特性計算結果中某參數X對應的溫度修正系數定義為KX,T2,其計算公式如下:

(1)

式中:XCOR,288.15為T2=288.15 K時參數X的換算參數;XCOR,T2為T2溫度下參數X的換算參數。

通常使用文獻[2]中的方法計算各性能換算參數的溫度修正系數曲線,具體做法是首先設定大氣壓力為101 325 Pa,溫度變化范圍為-35～40 ℃,計算間隔5 ℃,然后利用基于變比熱的發動機性能計算程序得到發動機的溫度特性,接著按照傳統的換算公式[4]將發動機的性能參數換算至海平面標準大氣條件下。標記其中288.15 K對應的換算參數為XCOR,288.15,其余溫度對應的換算參數為XCOR,T2。如此,即可按照式(1)計算各性能換算參數的溫度修正系數。為了提高總體性能計算的精度,本文所使用的程序采用文獻[17]中的自適應修正方法進行了修正。

按照文獻[3]中的規定開展溫度修正系數的驗證試驗,對計算獲得的溫度修正系數進行驗證。使用時,首先按照性能參數的相似換算方法[4,6]計算獲得當前溫度下的換算參數XCOR,T2,然后根據當前工作溫度T2在溫度修正系數曲線上插值獲得參數X的溫度修正系數KX,T2,最后,代入式(1)計算獲得XCOR,288.15。

1.2 溫度修正系數的驗證

按照GJB 378-87《渦噴渦扇發動機性能的溫度修正規范》給出的方法,計算了某型渦扇發動機中間狀態性能參數的溫度修正系數。并通過高空模擬試驗對計算獲得的溫度修正系數曲線進行了驗證,完成了進氣溫度為-17.8 ℃、-8.9 ℃、15.0 ℃、20.9 ℃、29.9 ℃條件下的溫度修正系數驗證試驗。

圖1給出了推力、發動機進口空氣流量和耗油率的溫度修正系數計算結果與高空臺試驗數據。由圖1可知,換算推力修正系數KFzj、換算空氣流量修正系數KWzj、換算耗油率修正系數Ksfczj的試驗數據與計算出的溫度修正系數曲線基本一致,各系數的最大偏差分別小于0.42%、0.41%和0.40%。可見,溫度修正系數的計算結果與試驗數據的一致性較好,滿足工程使用的需求。

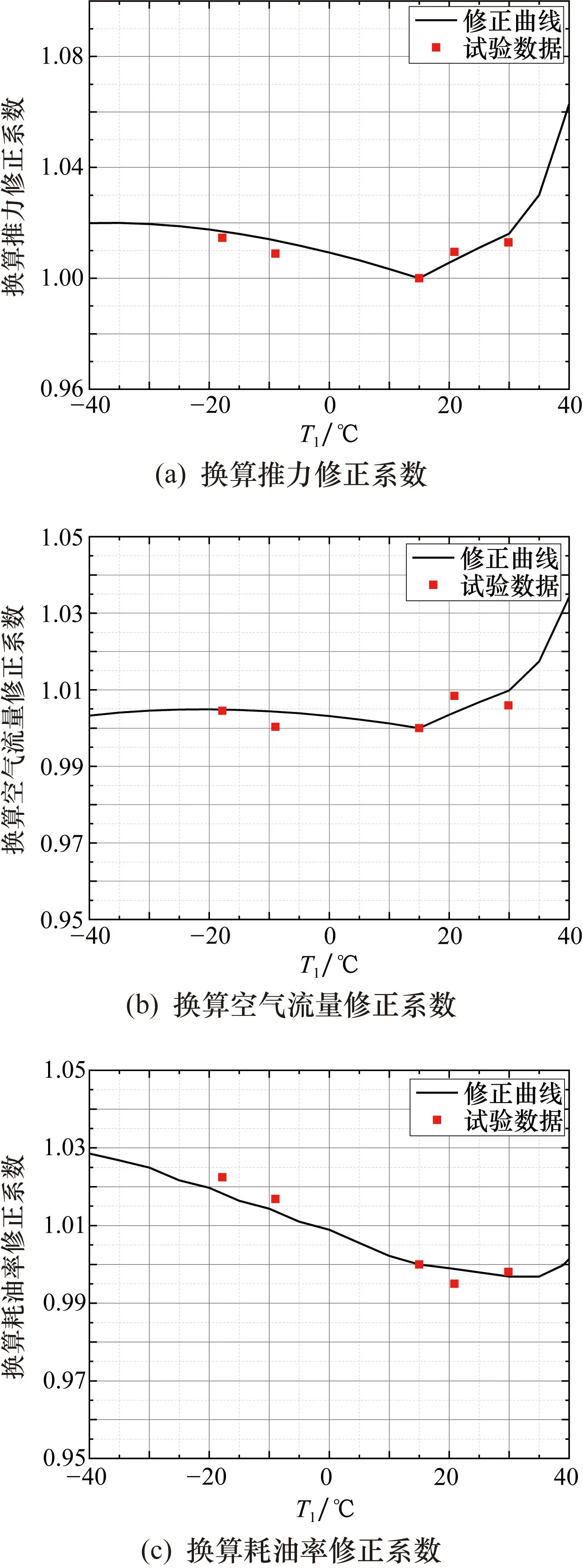
圖1 渦扇發動機中間狀態性能參數的溫度修正系數

在發動機進口總溫小于288.15 K時,該發動機中間狀態采用等發動機風扇換算轉速n1r的控制規律,按照發動機相似換算原理,在定換算轉速的情況下,發動機的換算參數應保持不變。但發動機溫度特性計算結果表明,進口總溫小于288.15 K時,發動機的換算參數會有微小差異,其表現為換算參數的修正系數不為1.0。其原因將在第2節中進行詳細討論。

2 影響溫度修正系數的因素

可從推導發動機性能相似換算參數時的假設條件[4,6]入手展開溫度修正系數影響因素的分析,這些假設條件包括但不限于:忽略雷諾數效應和發動機出口氣流中燃油的質量、工質的物性參數不受溫度影響、燃油的熱值保持不變。雷諾數效應的影響在地面臺架條件下可忽略不計,工質物性參數和燃油熱值的影響是本文分析的重點。同時,在等換算轉速段,發動機n1控制規律通常采用兩點線性插值,換算轉速并不嚴格相等,也會帶來微小的誤差。

下面通過發動機整機氣動熱力計算,定量分析上述因素對各換算參數的溫度修正系數的影響。

2.1 工質物性參數的影響

為了進一步定量分析不同因素對換算參數差異的貢獻情況,利用發動機整機性能計算程序開展評估計算。計算的思路是開發一套“基于定比熱的性能計算程序”,并將定比熱計算結果與變比熱程序計算結果進行對比。

開發“基于定比熱的性能計算程序”的方法是修改程序中的氣動熱力參數計算模塊,將定壓比熱容Cp、比熱容比k分別給定為1 062 J/(kg·K)和1.37,且不隨溫度和油氣比變化,同時相應更新焓、熵函數、音速等參數,并采用基于定比熱的氣動熱力計算子函數進行發動機整機性能計算。

在海平面靜止、等風扇換算轉速n1r條件下,在標準天到-40 ℃冷天區間內,對不同換算參數的修正系數進行分析。對比了基于定比熱和變比熱的換算參數的修正系數計算結果,具體如圖2所示。表1對比了兩種條件下,-40 ℃溫度修正系數相對變化量。

表1 -40 ℃溫度修正系數相對變化量對比

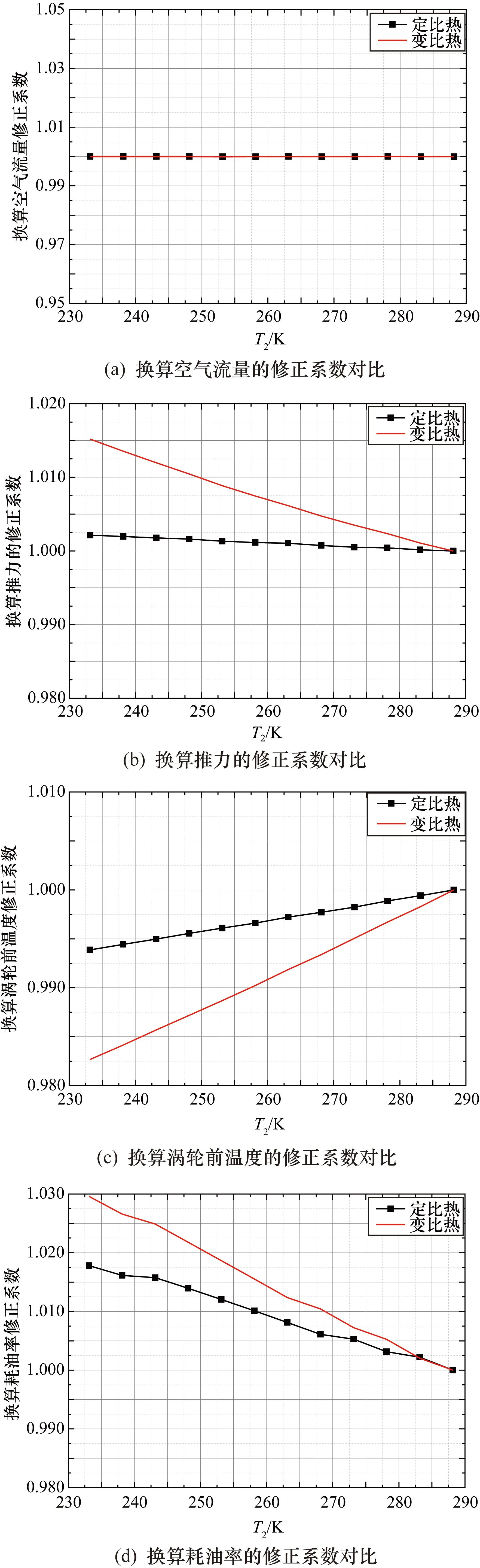
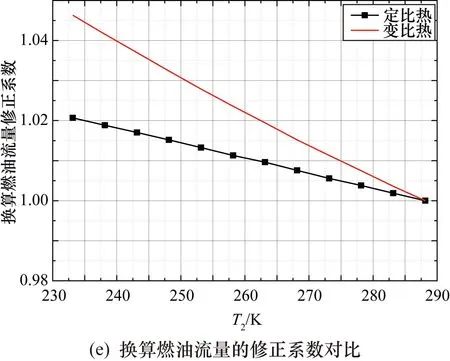
圖2 變比熱與定比熱不同換算參數的修正系數對比

可見,在定比熱情況下各換算參數的溫度修正系數更接近于1.0,表明工質物性參數是影響溫度修正系數的重要因素。其中變比熱計算發動機主要部件的Cp和k值如圖3所示。由以上分析可得如下結論。

圖3 Cp和k隨溫度的變化情況

① 換算空氣流量的修正系數始終為1.0,表明該換算參數不受大氣溫度的影響。

② 發動機推力取決于空氣流量和發動機單位推力(由發動機壓比(Engine Pressure Ratio,EPR)決定),在空氣流量一定的情況下,推力由EPR決定。圖2中換算推力修正系數的變化趨勢均與EPR修正系數的變化趨勢(圖4)相同,且在定比熱的情況下,二者的修正系數始終保持接近1.0,恰好驗證了上述論斷。這表明溫度變化時,工質物性參數變化引起EPR的修正系數產生變化,最終導致推力修正系數也產生變化。

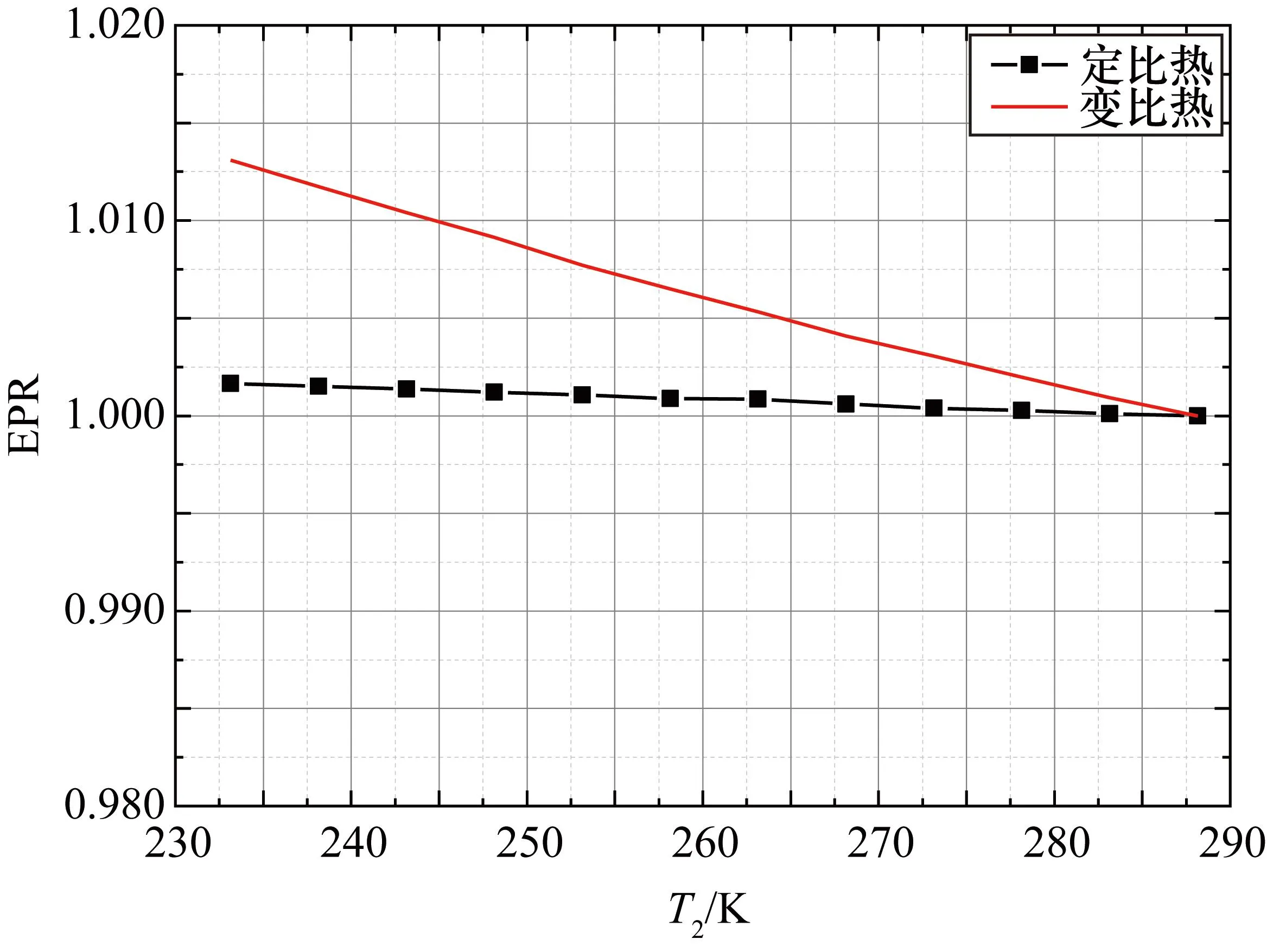
圖4 EPR修正系數變化情況

③ 在定比熱的情況下,燃油流量和耗油率的修正系數也大于1.0,在-40 ℃時修正系數約為1.02,這主要是因為低溫下燃油熱值升高所致,具體的量化分析過程將在下文中作詳細介紹。

2.2 燃油熱值的影響

上文的分析表明,在定比熱情況下,換算燃油流量和換算耗油率參數的修正系數與變比熱相比雖有所減小,但是仍不為1.0,在-40 ℃時,二者的修正系數約為1.02。其原因可從換算燃油流量(Wf)的推導過程進行分析。渦扇發動機主燃燒室簡化的能量平衡方程為

(2)

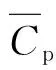
(3)

可見,燃油低熱值Hu為定值是燃油流量相似的條件之一。圖5展示了定換算轉速的情況下,燃油低熱值和有效熱值隨發動機進口總溫的變化情況。由圖5可知,燃油的等效熱值和低熱值均隨發動機進口溫度的降低而升高,這也正是定比熱條件下換算燃油流量的修正系數不為1的原因。

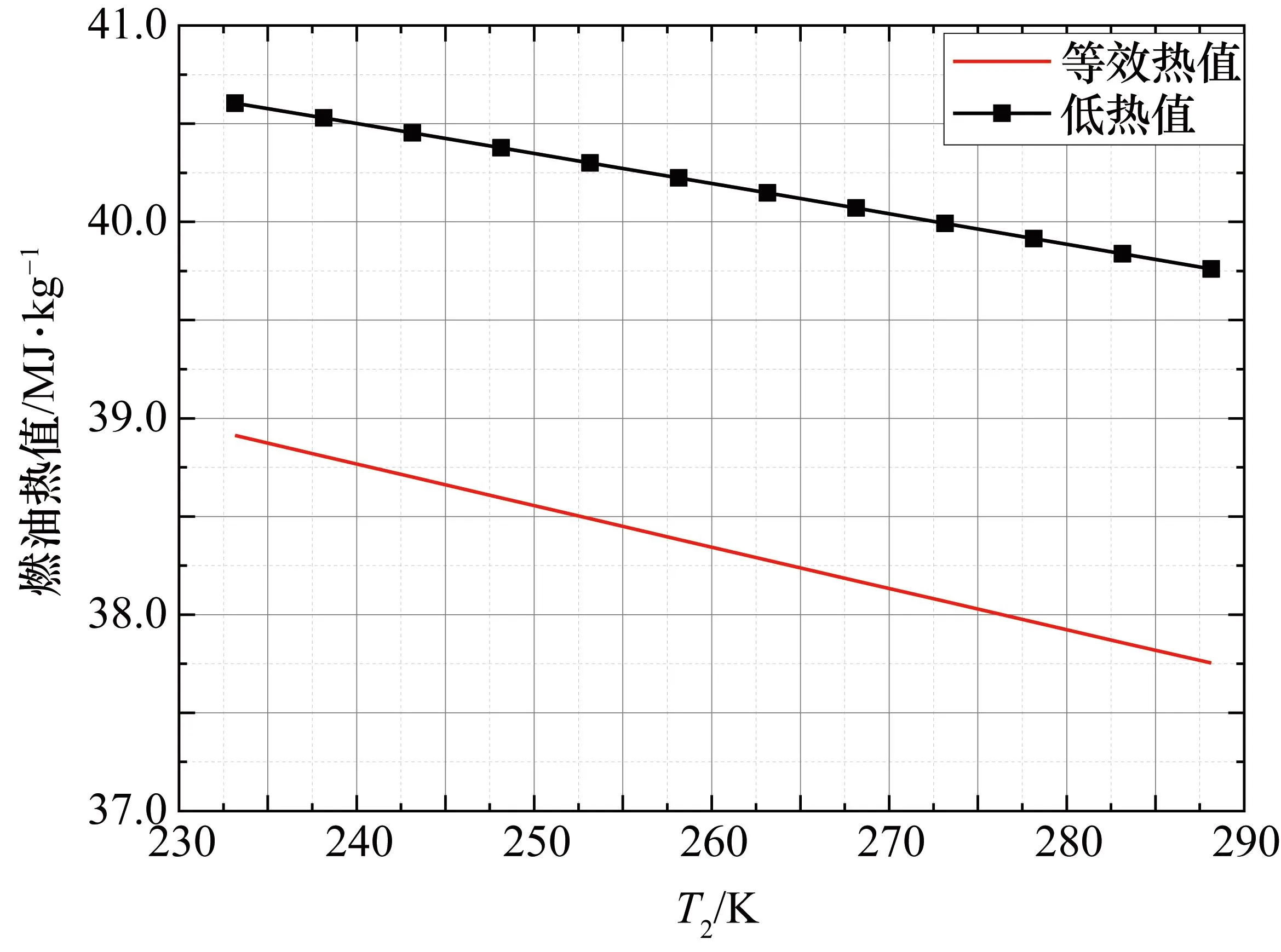
圖5 燃油熱值變化情況(定比熱)

為驗證上述結論,進一步固定燃油的低熱值,研究了發動機溫度特性,具體如圖6所示。需要注意的是發動機性能計算程序中為了簡化計算流程,使用了等效熱值的概念,而等效熱值為定值時,低熱值并不為定值。故需要進行迭代計算以確保燃油的低熱值為定值。

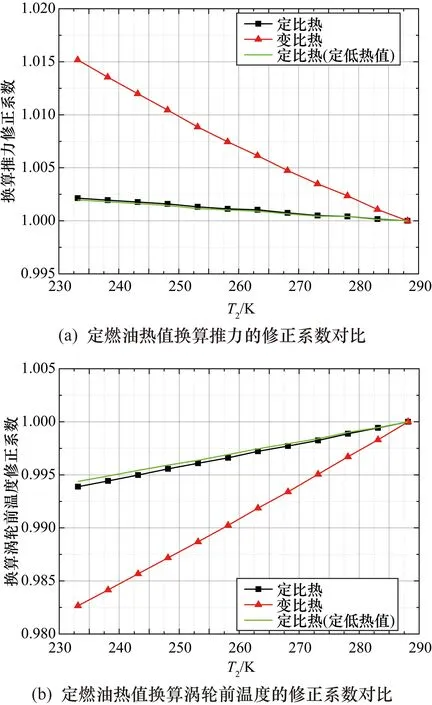
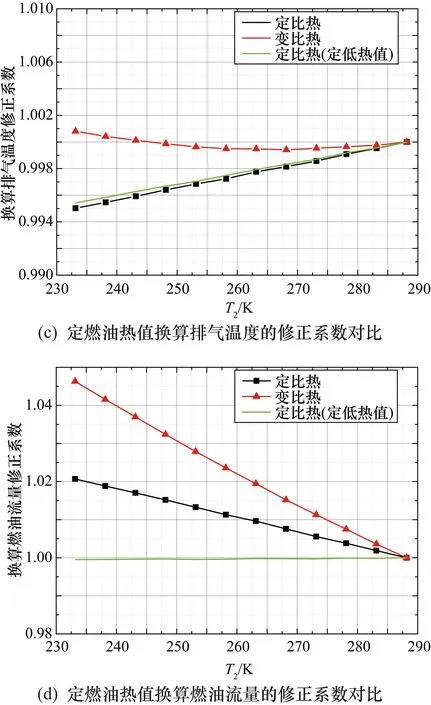
圖6 考慮定燃油熱值后變比熱與定比熱的修正系數對比

由圖6可見,在定比熱基礎上將燃油低熱值設置為定值后,溫度從標準天降低至-40 ℃時,換算燃油流量的修正系數始終維持在1.0。與燃油低熱值不為定值的情況對比:換算渦輪前溫度的修正系數變化減少約0.1%;換算推力的修正系數幾乎無變化。

在定比熱基礎上將燃油熱值設置為定值后,各修正系數在所研究的溫度范圍內的變化量分別為:換算推力約為0.2%,換算渦輪前溫度T4約為0.5%,換算燃油流量保持不變。部分參數的修正系數仍不為1,這可能與發動機性能計算程序的固有誤差引起的工作點的微小變化(見表2)以及換算參數推導過程中忽略油氣比的變化有關。從表2中的數據來看,風扇和壓氣機壓比稍有降低,喘振裕度增加,同時,風扇、壓氣機和高低壓渦輪的效率均略有降低(四大部件效率總共下降約0.1%)。而尾噴管進口油氣比Far7從0.017 1降低至0.013 9,在空氣流量保持不變的情況下,相當于噴管出口燃氣流量減少了約0.32%,在性能換算推導的過程中,Far7的變化被忽略。

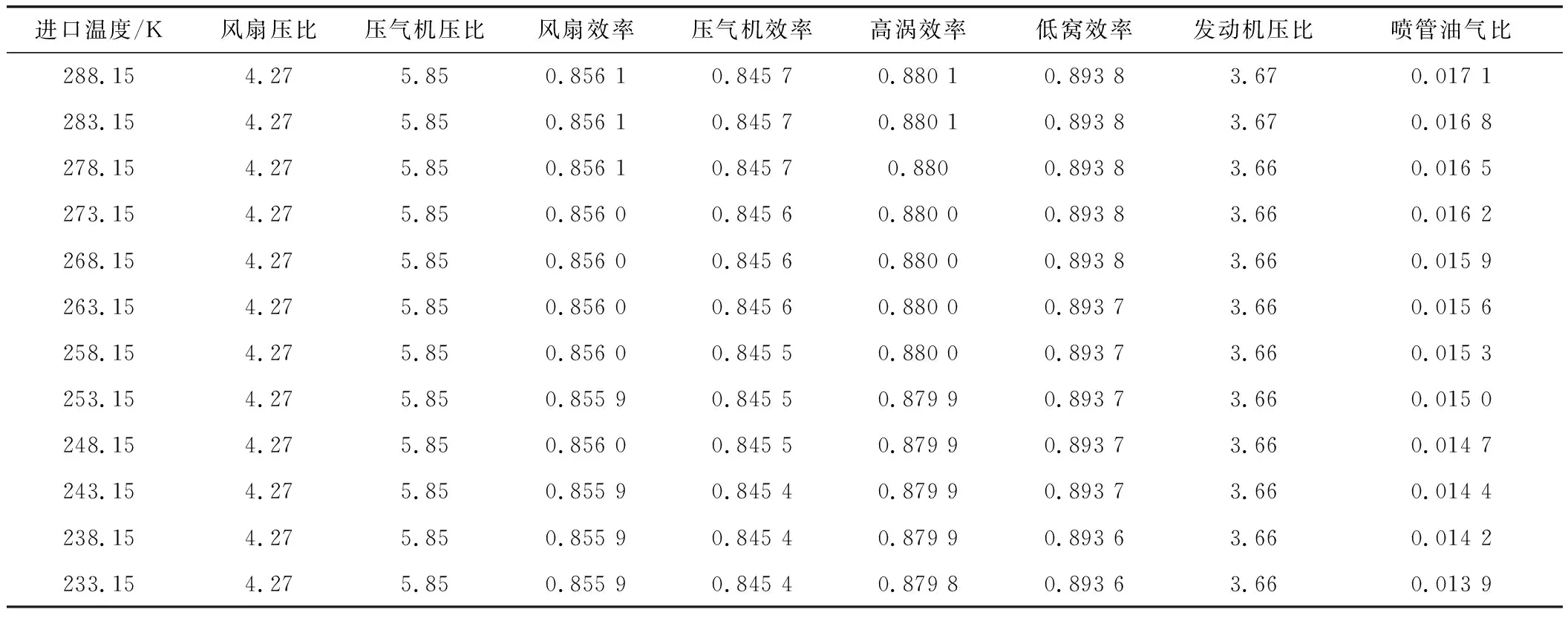
表2 主要部件參數變化情況(定比熱且定熱值)

2.3 控制規律插值誤差的影響

為了研究n1控制規律插值誤差導致的換算修正系數變化情況,對比了按照n1控制規律插值和固定n1r=1.0兩種情況下計算的換算推力修正系數,具體如圖7所示。可見,采用n1控制規律兩點插值的情況下將導致n1r小于1.0,最大下降量為0.22%,換算轉速偏低導致各換算修正系數的變化情況如下:

圖7 n1控制規律插值誤差對修正系數的影響

① 換算推力的修正系數比固定換算轉速的情況高(最大約1%);

② 換算燃油流量的修正系數比固定換算轉速的情況高(最大約1.1%);

③ 由于換算推力和換算燃油流量的修正系數均增加,因而換算耗油率的修正系數變化較小,僅比固定換算轉速的情況高約0.2%(溫度范圍內最大值);

④ 換算排氣溫度的修正系數比固定換算轉速的情況高(最大約0.4%)。

可見采用兩點插值的n1控制規律將顯著影響低溫天推力和燃油流量的換算參數,通過增加低溫天n1控制規律數據點可改善低溫天發動機性能狀態的一致性。

3 結論

通過本文的計算分析可得以下結論。

(1) 本文定量分析表明工質物性參數、燃油熱值和n1控制規律插值誤差是影響修正系數的主要因素。

(2) 在-40 ℃低溫天的情況下:

① 換算推力的修正系數主要受工質物性參數的影響,其次受n1規律插值誤差的影響;

② 風扇換算流量的修正系數始終為1,表明該換算參數不受大氣溫度的影響,唯一的誤差來源是n1控制規律插值誤差;

③ 換算排氣溫度和換算渦輪前溫度的修正系數誤差主要來自于物性參數的變化,其次受n1規律插值誤差的影響;

④ 換算燃油流量的修正系數主要受燃油熱值、物性參數的影響,其次受n1規律插值誤差的影響。

(3) 通過增加低溫天n1控制規律數據點可改善低溫天發動機性能狀態的一致性。