基于改進布谷鳥算法的機器人位置精度性能提升方法研究

李慰萱, 李 凱, 邢志勇

(上海寶冶集團有限公司,上海 201908)

隨著機器人技術的快速發展,工業機器人逐漸被應用于航天工業、衛星制造等高端制造領域[1-2]。“十三五”規劃期間的“智能機器人”重點專項指出,工業機器人應用于高端制造領域時,其絕對定位精度應優于0.05 mm。目前工業機器人的絕對定位精度仍僅為毫米級,尚無法滿足高端制造領域的精度要求。

引起工業機器人定位誤差的因素較多,而運動學參數誤差是影響工業機器人定位精度的主要誤差源之一[3]。機器人運動學參數誤差的標定步驟主要包含參數誤差模型建立、機器人誤差測量、誤差參數辨識和機器人誤差補償4個基本步驟。目前工業機器人廣泛使用DH模型、POE模型等,而在建立機器人運動學參數誤差模型時,還有ZRM模型、CPC模型等[4]。機器人誤差測量主要采用激光跟蹤儀、多拉線傳感器、立體視覺測量系統等。其中,激光跟蹤儀是目前機器人標定過程中最常用的測量設備[5]。但根據測量靶標的不同,能夠測量的機器人誤差數據分為位置誤差和姿態誤差。根據測量誤差數據的不同,可以建立位置誤差模型、距離誤差模型和位姿誤差模型[6]。由于當前工業現場對于位置精度要求較高,因此目前機器人標定技術中常用位置誤差模型除運動學參數誤差以外,還有柔性參數誤差和關節參數誤差等影響機器人精度性能的誤差[7]。在關節參數誤差中,減速比和耦合比參數誤差也會導致機器人精度的下降。

通過忽略高階項可以對誤差模型進行線性化,但所得到的誤差模型仍然是一個多參數的優化求解問題。傳統的最小二乘法、LM算法都受到目標函數的雅可比矩陣奇異性的影響,從而導致算法優化效果不穩定。除了傳統的優化算法以外,譬如粒子群優化算法、遺傳算法等智能算法能夠很好地避免雅可比矩陣奇異性的問題。溫秀蘭等[8]利用改進烏鴉優化算法實現Staubli TX60機器人的運動學參數誤差辨識,將該機器人位姿精度提升了70%。房立金等[9]基于量子粒子群算法實現了并聯機器人的運動學參數標定,將該并聯機器人的誤差從0.091 2 mm降低到0.010 8 mm。Liu[10]利用遺傳算法實現六自由度串聯機器人的運動學參數標定,將該機器人的位置誤差從8.72 mm降低到0.427 mm。喬貴方等[11]基于 BAS-PSO優化算法實現機器人的運動學參數辨識,將機器人的平均綜合位置誤差從0.312 0 mm降低為0.093 8 mm。以上文獻僅考慮了運動學參數誤差對機器人精度性能的影響,忽略了減速比參數等。為進一步提高機器人的標定效果,本文針對串聯機器人標定技術開展研究。首先建立了運動學參數和減速比參數的統一誤差模型,其次提出了一種改進布谷鳥搜索算法(Cuckoo Search Algorithm,CSA)以實現多參數的精確辨識,最后通過實驗驗證了該統一模型和改進布谷鳥算法的有效性。

1 串聯機器人誤差模型構建

1.1 運動學模型構建

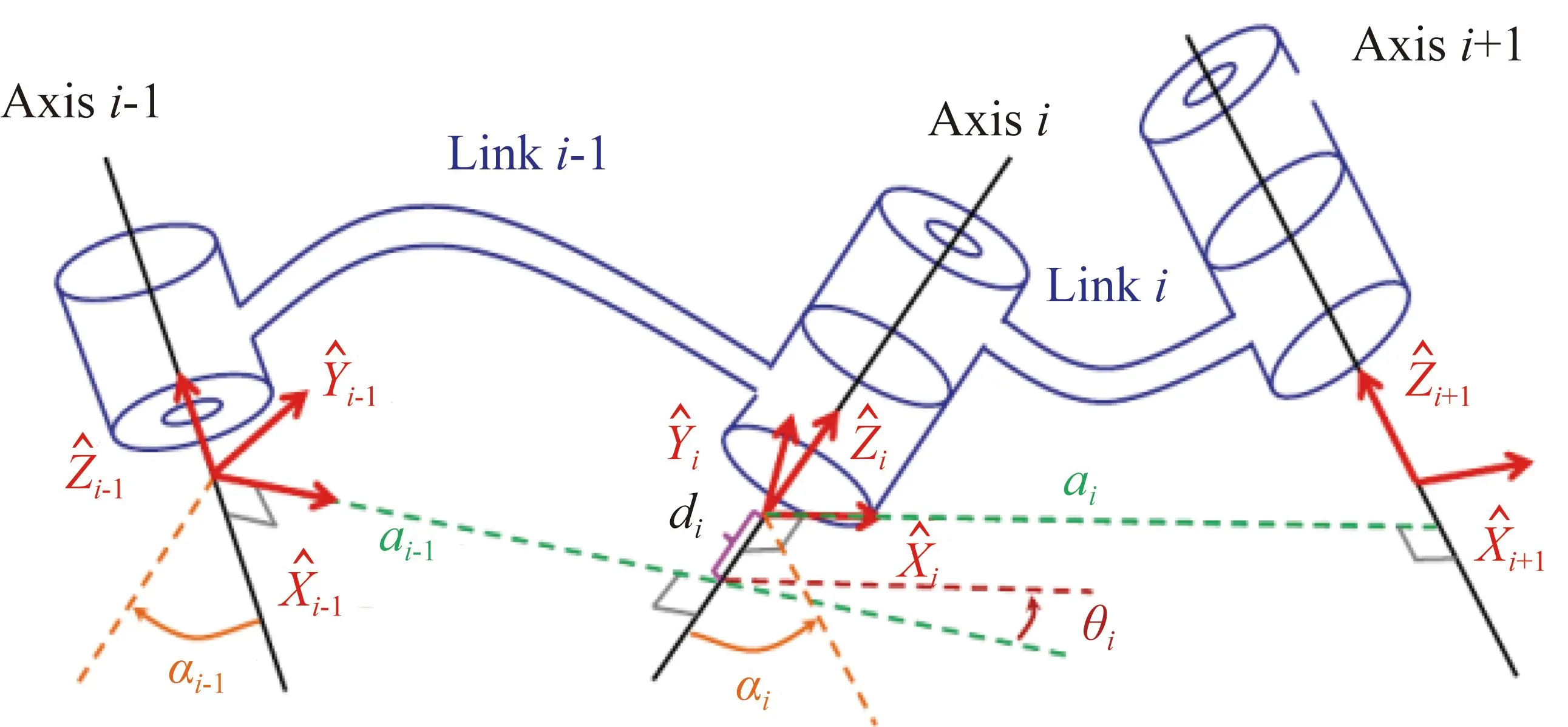
圖1 DH模型中的坐標系轉換

(1)

式中:i=1,2,…,6為自由度,即關節點;n為該轉換矩陣代入名義運動學參數值,即模型基座到機械手的矩陣量作乘。

而當相鄰兩軸平行或接近平行時,則存在奇異性問題。MDH模型在相鄰平行關節的描述參數上增加了角度參數βi[11],如式(2)所示。

(2)

1.2 減速比及耦合比參數誤差

減速比是指機器人關節減速機的傳動比值,一般關節編碼器安裝在伺服電機的末端,減速機安裝在伺服電機的輸出端,關節編碼器的值無法精確反饋機器人關節位置。因此,機器人關節每轉動一定角度都會造成一定比例的關節角度偏差,因此,本文在運動學模型的基礎上加入減速比ki和耦合比h兩個參數,其中減速比ki與關節角度名義值θni、關節角度實際值θri之間的關系如式(3)所示。

θri=kiθni

(3)

耦合比h僅存在于關節6中,該參數表示關節5對關節6的影響,h與關節角度名義值θn5、θn6和減速比k5和k6之間的關系如式(4)所示。

θr6=k6θn6+hk5θn5

(4)

將式(3)和式(4)代入運動學模型矩陣(2)中可以得到包含運動學參數、減速比參數和耦合比參數的統一模型表達式。

1.3 基于微分變換的位置誤差模型

機器人的名義末端位姿Tn矩陣可表示為

(5)

式中:Rn和Pn分別為名義旋轉矩陣和名義位置向量。

而實際情況中機器人的運動學模型參數ai、di、αi、θi、βi,減速比ki和耦合比h存在一定誤差Δai、Δdi、Δαi、Δθi、Δβi、Δki、Δh。因此,機器人實際末端位姿矩陣Tr可表示為

藜麥購買于沽源縣天然園農場；辛/癸酸甘油酯（MCT），印度尼西亞Britz Networks Sdn. Bhd.；尼羅紅，阿拉丁試劑有限公司，其它化學試劑均為國產分析純，實驗所用水為二級蒸餾水。

(6)

式中:Rr和Pr分別為實際旋轉矩陣和實際位置向量。

本文所采用的測量設備在能夠測量機器人末端位置的情況下,通過對Pn的每一列運動學參數進行微分,可以得到機器人的位姿誤差模型,如式(7)所示。

dP=Pr-Pn=HpΔη

(7)

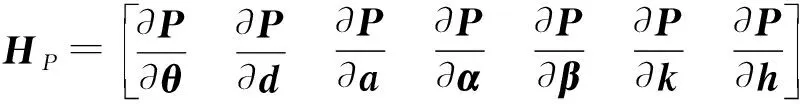
2 基于改進CSA的運動學參數辨識

2.1 改進CSA優化算法

CSA[12]是劍橋大學Yang教授提出的一種啟發算法。CSA是一種通過模擬布谷鳥的寄生育雛來求解最優問題的算法,該算法采用Levy飛行搜索機制,有效地提升了CSA的效率。典型的CSA算法流程如下所示。

① 隨機產生初始化種群,n個鳥巢位置;

② 根據目標函數計算適應度,計算并保留最好的鳥巢位置;

③ 根據Levy飛行更新鳥巢位置;

④ 計算新位置的適應度,并同原鳥巢的適應度對比,擇優保留;

⑤ 將發現概率Pc與代表外來鳥蛋被發現概率的隨機數作比較,若發現概率Pc較大,則重新隨機生成一個新鳥巢位置并計算適應度;

⑥ 若滿足終止條件,輸出最好的鳥巢位置,否則回到步驟③。

CSA的尋優效率受限于Levy搜索策略,Levy搜索步長和方向的隨機性很大,如圖2所示。基于Levy搜索的CSA收斂速度慢,求解精度低,易陷入局部最優。為了提高算法求解效率和精度,本文引入對數調整系數修正Levy搜索步長,從而提高算法的全局收斂性和收斂速度。在迭代前期,對數調整的系數曲線下降更快,從而有利于全局探索、快速定位最優解的大致范圍;在迭代后期,對數調整的系數曲線下降平緩,有利于局部精細搜索,進而找到全局最優解。因此,本文采用的對數調整系數如式(8)所示。

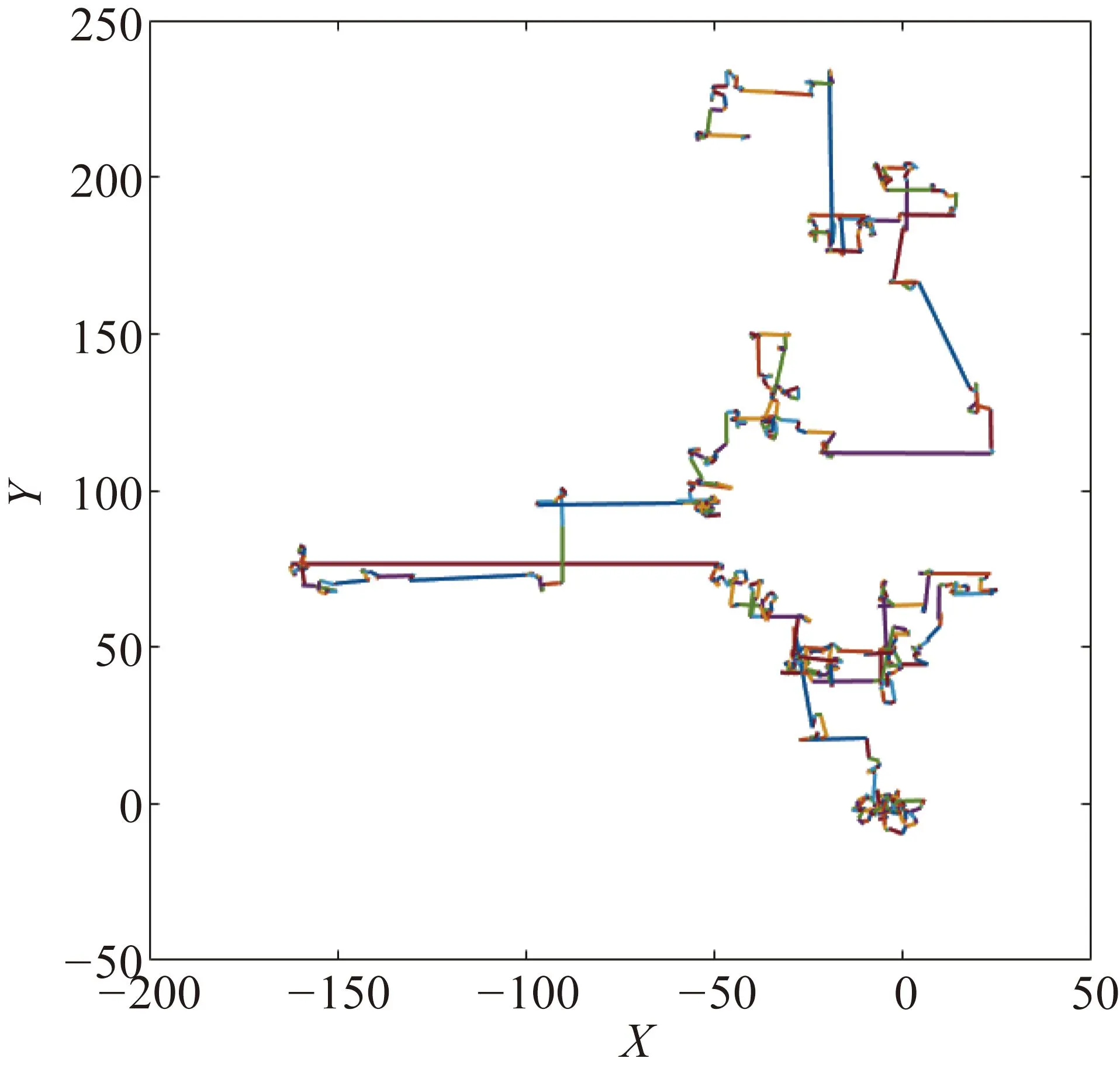
圖2 CSA中Levy維飛行軌跡

(8)

式中:Xi為第i維迭代參數;t為當前迭代次數;κmax,κmin為κ的初值和終值;η為對數調整系數;max_number為最大迭代次數。本文設定κmax=0.9,κmin=0.4,η=1,max_number=1 000。

2.2 機器人參數辨識的適應度函數

采用改進CSA優化計算機器人誤差參數誤差時,其適應度函數如式(9)所示。該適應度函數是運動學參數、減速比參數和耦合比參數誤差集(Δai,Δdi,Δαi,Δθi,Δβi,Δki,Δh)的函數,通過改進CSA優化算法搜索誤差參數,使適應度函數f為最小。在優化過程中搜索誤差參數的取值范圍定為[-1,1]。

(9)

式中:N為標定點數目,一般為50。

3 運動學參數誤差標定實驗

本文所搭建的機器人標定試驗系統使用Leica AT930激光跟蹤儀和Staubli TX60工業機器人,如圖3所示。相關數據處理軟件是Spatial Analyzer和MATLAB。本文待標定的Staubli TX60工業機器人的重復定位精度為±0.02 mm,額定負載為3 kg。所涉及的測量過程均符合GB/T 12642-2013《工業機器人 性能規范及其試驗方法》標準[13]。實驗中以機器人的基坐標系為參考坐標系,在Staubli TX60工業機器人前方的正方體空間內隨機選擇160個測量點,并且保證測量點能夠盡可能地分布在立方體的空間內,其中110個測量點作為參數辨識數據集,50個點作為模型參數驗證數據集。為評價機器人精度性能參數的提升效果,本文定義了平均綜合位置誤差如式(10)所示。

圖3 工業機器人標定實驗系統

(10)

式中:M為數據集中的測試點個數。

本文待標定的機器人參數名義值如表1所示,利用改進CSA優化算法辨識機器人的運動學參數誤差如表2所示。具體辨識數據集和驗證數據集的處理結果如圖4所示。辨識點集中的Staubli TX60機器人的平均綜合位置誤差從0.648 5 mm降低為0.062 9 mm,機器人的位置精度性能提升了90.3%,驗證點集中的Staubli TX60機器人的平均綜合位置誤差從0.646 4 mm降低為0.085 9 mm,機器人的位置精度性能提升了86.7%。從而說明,經過改進CSA算法辨識得到的機器人運動學參數誤差、減速比參數誤差以及耦合比參數誤差值更符合機器人實際結構參數。同時也驗證了本文提出的運動學參數、減速比參數和耦合比參數的統一建模,能夠有效地提升機器人的精度性能。

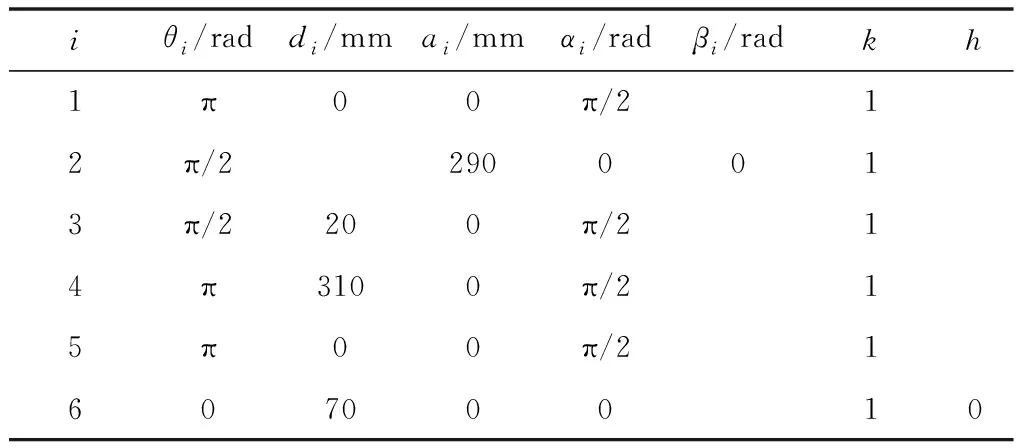
表1 Staubli TX60機器人的名義參數

表2 待標定機器人的參數辨識誤差值

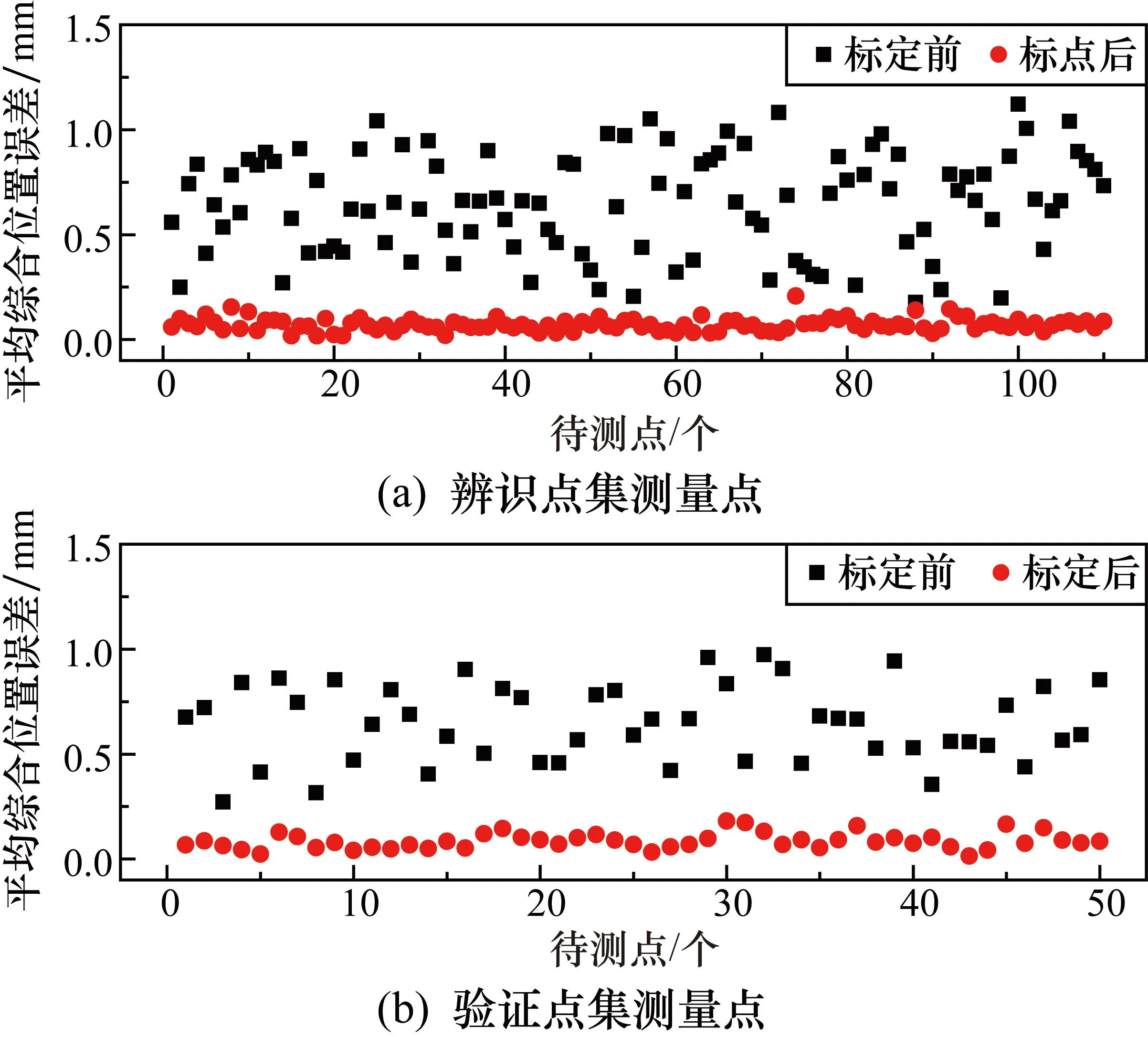
圖4 Staubli TX60機器人標定前后的實驗結果對比

4 結束語

本文首先闡述了工業機器人關節誤差和運動學誤差的統一建模方法,將關節的減速比參數和耦合比參數與運動學參數進行統一建模;其次提出了一種改進CSA優化算法的多參數辨識方法,采用對數調整系數修正Levy搜索步長,提升了算法的收斂性和精確性。為了驗證以上模型和辨識方法的有效性,本文構建了串聯型工業機器人標定實驗系統。通過在Staubli TX60機器人的運動空間內測量160個測量點,分別構成辨識點集和驗證點集。實驗結果表明,利用本文提出的誤差模型和辨識方法,能夠將機器人位置誤差降低86.7%以上,能夠將辨識點集中的Staubli TX60機器人的平均綜合位置誤差從0.648 5 mm降低為0.062 9 mm,相較于優化前機器人位置誤差降低為0.072 2 mm,模型定位誤差進一步降低了12.9%;同樣,利用本文提出的誤差模型和辨識方法,驗證點集中的Staubli TX60機器人的平均綜合位置誤差從0.646 4 mm降低為0.085 9 mm,相較于優化前機器人位置誤差降低為0.090 2 mm,模型定位誤差進一步降低了4.77%。本文提出的改進CSA優化算法能夠較好地提升工業機器人的精度性能。