基于RRT 森林算法的高層消防多無人機室內協同路徑規劃

陳錦濤 李鴻一 任鴻儒 魯仁全

隨著城市化進程加速,高層建筑數量急劇增加,而高層建筑火災事故給現有的消防救援技術與設備帶來了新的挑戰[1-2].現有的消防舉高設備通常無法觸及高于18 層的起火樓層,消防官兵負重登樓代價大[3-4],建筑內部環境復雜,充滿高溫煙塵,人員疏散極其困難[5].此時,基于多無人機 (Multi-unmanned aerial vehicles,Multi-UAVs) 協同控制技術的高層消防救援方法,在高層建筑消防滅火中的應用愈發廣泛[6-8].多無人機可通過破窗,迅速進入高層火災現場,嘗試撲滅初期火災[9];在室內飛行時實現自主避障、自主探測火點及被困人員;可通過揚聲器、照明燈等輔助設備協助被困人員撤離[10].多無人機協同控制現已成為控制領域的研究熱點[11].在高層火災現場的室內環境進行多無人機協同路徑規劃、協同救援的研究,其難點在于規劃空間小、避障裕度低、限制條件多[12]等.

無人機路徑規劃算法主要有可視圖法、柵格法、快速遍歷隨機樹法(Rapidly-exploring random tree,RRT)等[13].其中,RRT 算法因不需要對環境進行精確建模,搜索性較強,以及對時變環境適應性良好等優勢[14],在路徑規劃領域中有著廣泛的應用.對于RRT 算法及其改進型算法,文獻[15]在前人的研究成果上對RRT 算法進行了總結,主要包括雙向RRT (Bidirectional RRT,Bi-RRT)、偏向目標RRT (RRT-Goalbiasing) 以及RRT-Connect 算法,并以此為基礎提出了基于人工勢場法的改進RRT 算法,一定程度上提高了算法的路徑規劃效率,減少了路徑規劃時間.文獻[16-17]研究了動態步長RRT 路徑規劃算法,提高了隨機樹擴展的效率.然而,上述改進算法為提高到達終點的速度,傾向于采用降低搜索廣度的方法對RRT 算法進行優化,這樣的優化對于復雜的高層室內火災環境來講是難以適用的.有學者[18-21]曾提出在確定的位置上增加少量隨機樹以解決此問題,但該方法更傾向于通過人工干預的形式選擇輔助隨機樹根節點的位置,不適合根據高層火災室內環境變化頻繁重規劃.針對以上問題,本文提出一種改進的插入隨機中間樹的多樹RRT 算法,下稱RRT 森林算法.

考慮路徑的可行性,現有的RRT 算法普遍存在路徑與障礙物距離過近的問題.目前常見的解決方法是把地圖進行膨脹處理再進行路徑規劃[22],但對于需要實時進行路徑規劃的復雜高層消防環境,對地圖進行預處理會降低規劃效率.文獻[23]提出一種人工勢場優化的RRT 算法,但這種方法需要計算地圖中的勢場,需要反復計算微分,運算效率仍不高.因此,研究一種能確保無人機與障礙物之間保持安全距離的碰撞檢測程序十分有意義.

此外,RRT 算法得到的路徑通常不是最優路徑[15],而是一條有冗余點的路徑.在文獻[24]中,Jeong 等提出Quick-RRT*算法,在每一次產生子節點時都在給定的深度范圍內,尋找無障礙物相隔的父節點進行連接,減少冗余點的產生,但其路徑受制于RRT 生成的節點,易出現不合理的拐角.針對這一問題,本文提出兩次動態規劃(Dynamic programming,DP)對路徑進行優化的方法,采取“規劃-插值-規劃”的策略取得可行性更高的路徑.

基于對上述國內外研究現狀的調研與分析,綜合考慮高層消防多無人機路徑規劃時間緊迫、環境復雜、需要頻繁對未執行的局部路徑進行重規劃[25],以及需要同時規劃多條路徑的特性,本文提出RRT森林算法,并通過改進的障礙物接近檢測方法,以及動態規劃的兩次優化,提高算法的可行性.主要工作歸納如下.

1 ) 提出RRT 森林算法.通過提升隨機樹森林的搜索廣度,提升算法搜索效率.與文獻[18-21]不同,RRT 森林算法以樹間連接優先的策略,降低搜索后期節點數量對遍歷效率的影響,從而適應高層火災救援任務中頻繁的路徑重規劃;同時,RRT 森林算法通過多樹連接進行尋路的設計,實現多起點多終點的多無人機協同路徑規劃.

2 ) 提出障礙物接近檢測方法.通過檢測包絡線控制點以及包絡線內部的隨機點,考慮無人機的體積,使得路徑更遠離障礙物.

3 ) 提出基于動態規劃的冗余點移除方法.通過對路徑中的節點以最優的方式重新連接,刪除其中的冗余點,分離多無人機重合的路徑,并得到節點稀疏且路程最短的路徑.

本文算法流程如圖1 所示.第1 節分析了基本RRT 算法及雙向RRT 算法的優缺點;第2 節和第3 節分別闡述了RRT 森林算法和基于動態規劃的冗余點移除方法;第4 節為RRT 森林算法的仿真研究;第5 節為結論.

1 RRT 算法及其改進

為滿足高層消防多無人機協同路徑規劃中的時間緊迫性要求,本文提出RRT 森林算法.RRT 森林算法通過增加隨機樹的數量達到提升搜索廣度的目的,從而提升算法在復雜環境下的路徑搜索效率.在闡述RRT 森林算法之前,首先對基本RRT 算法與雙向RRT 算法進行簡單的描述.

1.1 基本RRT 算法

RRT 算法是由Lavalle 于1998 年提出的一種基于隨機采樣的快速路徑規劃算法,是一種概率完備算法[15,26].該算法的優點是節點擴展不需要進行預處理,根據當前的環境信息快速搜索可行路徑,可用于無人機路徑規劃上.

RRT 算法的基本思想是: 以起點為根節點,通過在地圖上隨機采樣,并以最近的節點為父節點,產生相應的子節點,使隨機樹不斷擴展.當隨機樹接近終點并與終點連接,即完成路徑搜索.隨機樹的采樣及搜索過程如圖2 所示.

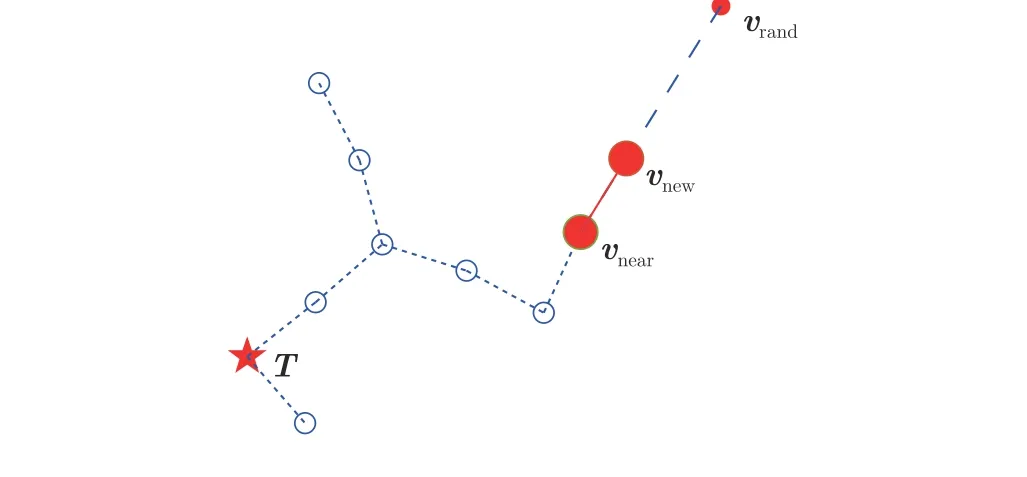
圖2 基本RRT 算法采樣及搜索過程Fig.2 Sampling and exploring process of basic RRT

基本RRT 算法的優點在于不需要對環境模型進行復雜處理,即可進行路徑規劃.但傳統RRT 算法的缺點主要有:

1 ) 由于RRT 算法是通過隨機采樣驅動尋找路徑,得到的路徑曲折,通常不是最優路徑;

2 ) RRT 算法在隨機采樣后需要遍歷隨機樹上現有的節點,之后選擇最近的節點vnear,方能在vnear附近朝著采樣點vrand的方向前進一小步到達vnew.然而,在復雜環境下,路徑搜索之初,隨機樹上節點少,覆蓋范圍小,生成vnew的成功率顯著降低,隨機樹在小范圍內重復搜索,會導致路徑規劃收斂緩慢.

高層建筑火災的室內環境往往是復雜時變環境,需要頻繁重規劃路徑的環境,因此我們需要解決傳統RRT 算法前期搜索效率低的問題,使之能夠高效完成復雜環境下的路徑搜索.

1.2 雙向RRT 算法

雙向RRT 算法與基本RRT 算法不同之處在于,以起點和終點為兩個根節點,分別建立隨機樹進行搜索,直到雙方節點彼此接近,最終將兩棵樹最接近的子節點連接[26].雙向RRT 兩棵樹連接示意圖如圖3 所示.

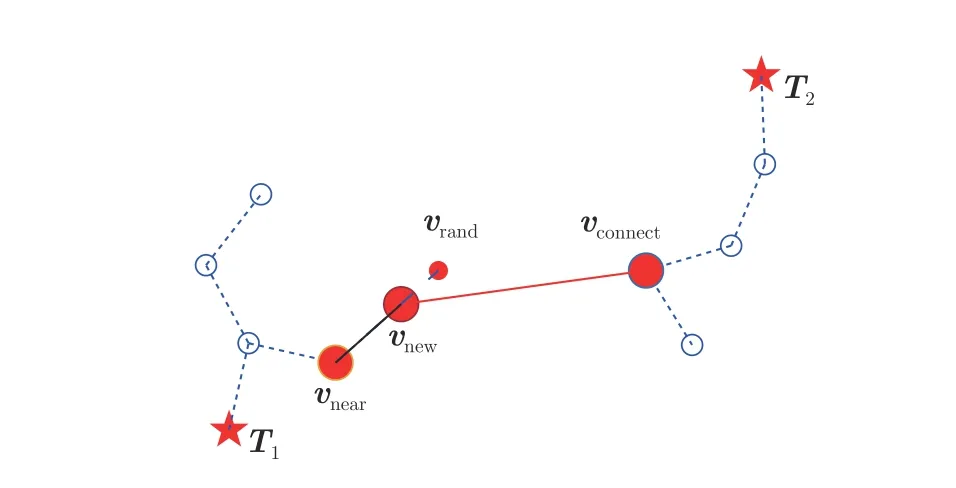
圖3 雙向RRT 連接過程Fig.3 Connecting process of bidirection-RRT

與基本RRT 算法相比,雙向RRT 算法在終點處增加一隨機樹,從起點和終點同時搜索路徑,在搜索速度上具有一定優勢,一定程度上增大了搜索初期的搜索廣度.但隨著環境復雜度的提高,雙向RRT 的兩個隨機樹,在搜索初期仍會被局限在小范圍內,不能滿足高層消防救援中頻繁進行路徑重規劃的需求.

2 RRT 森林算法

為提升RRT 算法在高層火災現場內部的路徑搜索效率,適應高層消防救援中頻繁進行路徑重規劃的任務需求,本文提出RRT 森林算法,在可行區域內隨機選點生成隨機樹,并與其他隨機樹相連接,從而得出多組路徑.

通過多樹優化的RRT 算法的思路并非首次提出,受雙向RRT 算法增加隨機樹提升搜索廣度的啟發,鐘建冬[18]提出可以將RRT 算法從兩棵隨機樹進一步擴展為三棵樹,直至多樹.Devaurs 等[20]利用多樹的特性對Transition-RRT 進行優化,通過給定根節點的方式在地圖中生成多個隨機樹,提升了搜索效率.然而,上述文獻中的多樹RRT 算法為隨機樹擴展優先的形式,這會導致在搜索連接對象時遍歷量較大.對此,本文提出的RRT 森林算法采用樹間連接優先策略,能夠有效減少遍歷量,進而提升搜索效率.另外,針對文獻[20]中導出路徑需要經過所有隨機樹的根節點、路徑合理性較差的問題,本文通過設計一種適用于多樹RRT 的路徑導出方法予以解決.綜上所述,本文所提出的RRT森林算法具有以下特點: 1)隨機樹連接優先,通過檢查vnear判斷是否可以與其他隨機樹連接,一旦進行連接,則不再擴展隨機樹;2) 利用多隨機樹的特點進行多起點多終點的路徑規劃;3)導出路徑不必經過每棵樹的根節點,因此能夠取得節點更少的路徑.

RRT 森林算法的主要工作原理是: 在地圖中增加隨機點,并以這些隨機點以及原有的起點和終點為根節點,各自生成隨機樹.隨著隨機樹的生長,地圖上可行的區域會迅速被隨機樹覆蓋,就像一片森林,因此稱這種算法為RRT 森林算法.基于該算法的特性,隨機樹之間可以通過樹枝與其他樹相互連接,最終將起點與終點連通,從而完成路徑搜索.RRT 森林算法分為搜索過程、隨機樹之間的連接與合并過程以及路徑導出過程三個部分.

2.1 RRT 森林算法搜索過程

定義一個由k架無人機完成的多起點多終點的高層消防多無人機協同路徑規劃任務,記地圖為M.設需要規劃n(n ≥k) 條路徑,記第i條路徑的起點、終點分別為,其中,i=1,2,···,n,,并滿足以下假設:

假設 1.考慮到多無人機路徑可能出現交叉的問題,每架無人機之間以及無人機與地面之間至少需保持α米距離.無人機的高度隨地面起伏而變化,當需要改變高度時,無人機會加強對附近無人機的監測.

注 1.若地圖中某處v∈M可行高度范圍為[v.floor,v.ceil],暫且假設該范圍足夠讓n架無人機在不同高度同時飛行,k架無人機從低到高排列時,第j(j=1,2,···,k) 架無人機在v點的飛行高度vj.z可表示為

而第j架無人機設定的距地面高度則等于 (j+1)α.另外,由式(1)可得到k架無人機飛行所需垂直空間條件為

滿足條件(2)方可保證多無人機能同時通過該點.因此,路徑規劃使用的灰度地圖中,不滿足條件(2)的區域視作不可行區域.

現用RRT 森林算法搜索n條路徑,其過程如下:

2 ) 開始隨機搜索.搜索過程采用樹間連接優先的策略.對于隨機樹集合T,在每次迭代中逐一進行搜索.首先,對于當前活動樹Tme采樣得到隨機點vrand,并查找節點vnear∈Tme,使得vrand與vnear距離最短;其次,先判斷vnear在給定范圍內是否有非活動隨機樹的節點vconnect,并確定vnear與vconnect之間有無障礙物,若存在連接無障礙的vconnect,則連接vnear與vconnect,并結束對當前樹的搜索;反之,按照基本RRT 的方式沿vnear到vrand方向,以步長s,嘗試在Tme上新建一個子節點vnew,并結束對當前樹的搜索.RRT 森林算法搜索路徑分為連接和生長兩種工作模式,其工作原理如圖4所示,其中圖4(a)為隨機樹之間的連接過程,圖4(b)為隨機樹的生長過程.

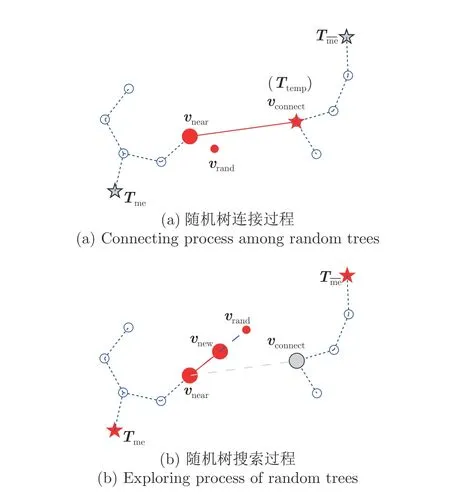
圖4 RRT 森林算法兩種工作模式Fig.4 Two working modes of RRT-forest algorithm

3 ) 當所有隨機樹均嘗試進行一次搜索后,逐一判斷樹Tk ∈T是否已經包含所有起點與終點,若已全部包含,則搜索完成,否則繼續進行下一次迭代.若算法一直無法達到搜索完成條件,則迭代會在迭代次數達到最大迭代次數m時停止并顯示錯誤信息.RRT 森林算法隨機樹搜索過程偽代碼如算法1 所示.

算法 1.RRT 森林算法隨機樹搜索過程

2.2 多隨機樹的連接與合并

對比于雙向RRT 的連接方式,多隨機樹之間的連接方式增加了合并步驟,以防止節點連接關系混亂.由于RRT 森林算法中每棵隨機樹需要進行多次連接,因此不得不考慮隨機樹被連成閉環的問題.從路徑規劃的角度看,一旦隨機樹被連接成環,在結束搜索后,導出路徑時會陷入死循環.而從隨機樹的樹狀結構看,隨機樹連接成環將會破壞樹狀結構,導致部分節點連接關系混亂.

為了避免多隨機樹連接成環狀造成路徑規劃出錯的問題,在連接的同時將兩棵隨機樹合并,從而防止兩棵樹之間多次連接.此外,兩棵隨機樹的合并需要重新選擇父節點.根據隨機樹的樹狀結構,可以將任意節點定義為新的根節點,但需要先調整新根節點到原根節點之間各段的連接關系,再對其他節點重新建立連接關系.隨機樹之間的連接過程如圖4(a)所示,具體操作如下:

2.3 多路徑的導出

多無人機協同執行高層消防任務時,往往需要為多架無人機分別導出路徑,本文結合RRT 森林算法的特點,設計了一種導出RRT 多路徑的方法.主要工作原理如圖5 和算法2 所示.

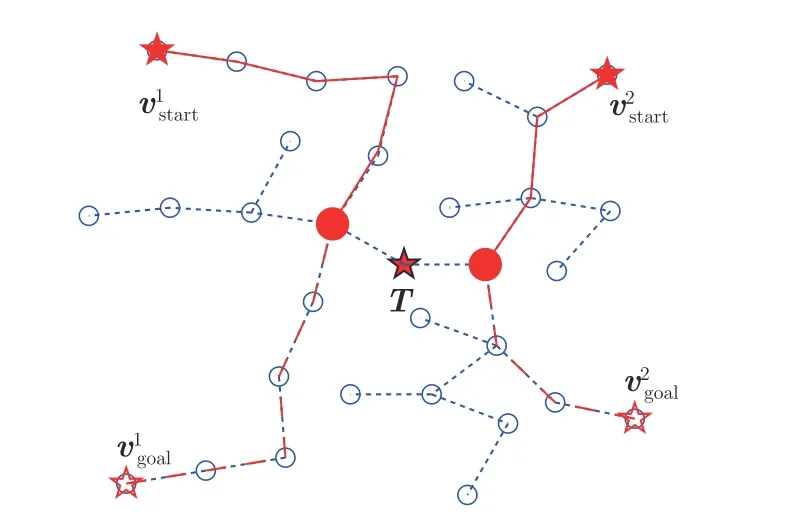
圖5 多路徑的導出方法Fig.5 Export method for multiple paths

由于存在多條路徑,因此每條路徑是分別確定的.而相較于文獻[20]所述的方法,本文所導出的路徑可不經過全部根節點.具體工作原理為: 對于第i架無人機,其起點為,終點為,所在隨機樹被提取,記為T*.

定義序列Rfrom和Rto,分別從起點和終點開始,向T*的根節點的方向,不斷尋找父節點并記錄,直到Rfrom和Rto出現重復元素.然后令R=Rfrom∪Rto,即完成路徑導出.路徑導出過程的偽代碼如算法2 所示.

算法 2.路徑導出過程

注 2.在程序實現的過程中,Rfrom和Rto記錄的是各節點在樹T*上的編碼,因此,需要在樹T*上根據R中的編碼查出具體的路徑坐標并組合成序列Pi,即為第i架無人機的路徑.

2.4 改進的障礙物接近檢測方法

RRT 算法常用的碰撞檢測是通過檢測地圖中某點的灰度值判斷該點是否在障礙物上,對于線段的碰撞檢測,則從起點到終點逐個點檢測是否在障礙物上,一旦發現線段上某個點在障礙物上,則判斷線段存在碰撞.特別地,對于變步距RRT,可以通過碰撞檢測程序反饋推薦步長進行變步距搜索,一定程度上提高了RRT 的搜索效率.然而,由于碰撞檢測未能考慮無人機的體積,加之地圖可能存在誤差,在實際執行中,無人機存在與障礙物剮蹭的風險.對于這個問題,常用的解決方法多是通過圖像處理技術對圖像中障礙物進行膨脹處理,這需要花費時間對圖像進行預處理,對于需要頻繁進行部分路徑重規劃的高層消防多無人機系統來說是難以實現的.基于上述情況,本文提出一種改進的障礙物接近檢測方法,其思想是將單點檢測轉化為一種對包絡線外緣主要控制點的檢測,在考慮無人機體積的同時,盡可能減少路徑規劃速率的損失.

待測點vtest在灰度地圖M上判斷是否可行步驟如下: 首先,地圖M以深色表示不可行區域,定義安全距離r;然后,取無人機包絡線的頂點,以及在這些頂點所圍成的區域內,根據計算機算力,隨機選取測試點=1,2,···,k,加上待測點vtest自身;最后通過分析在M上這些測試點的取值,判定待測點vtest是否可行.當且僅當上述點全部位于可行區域時,待測點vtest可行.

改進的障礙物接近檢測圖如圖6 所示,假設采用的是四旋翼無人機,圖中待測點記為vtest,圓表示無人機的旋翼,淺色實線段組成無人機的框架,正方形點表示無人機包絡線的頂點,記為vA,vB,vC,vD,連接這四個點的虛線框為無人機包絡線,中間正方形點表示無人機的中心位置,即vO,而三個“*”號點則是隨機選取的測試點=1,2,3.圖6中,雖然中心點vO為可行點,但vB,vD和一個白色“*”號表示的隨機點位于不可行區域,因此,本例中待測點vtest不可行.

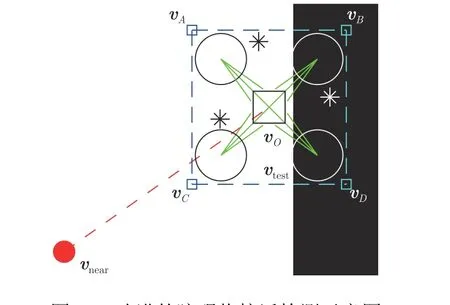
圖6 改進的障礙物接近檢測示意圖Fig.6 Schematic diagram of the improved obstacle proximity detection

對于線段碰撞檢測,從線段的一端向另一端逐步進行上述的障礙物檢測,其中每一步間隔一個安全距離r.當檢測到第k步不可行時即停止檢測,并返回可行步長=r(k-1).

在RRT 森林算法中應用此種障礙物檢測方法,可以在未經膨脹處理的地圖中進行路徑規劃,同時不致使無人機過于接近障礙物而發生碰撞,提高了路徑的可行性.

3 基于動態規劃的冗余點移除方法

在高層火災所造成的未知、時變且復雜的環境中,直接使用RRT 森林算法搜索的多路徑會出現以下問題: 1) 路徑非最優,會造成不必要的時間和能力開銷;2) 路徑會出現重疊,雖然每架無人機以不同的高度飛行,但無人機仍會相互影響.因此,有必要移除路徑中的冗余點,并減少路徑重疊,實現路徑的進一步優化.

3.1 動態規劃

動態規劃是上世紀50 年代美國學者Bellman提出的一種最優化規劃方法[27].動態規劃用一個遞推關系式,使決策過程連續地轉移,并將一個多步最優控制問題轉化為多個一步最優控制問題,從而簡化求解過程.對于N級決策過程,其動態方程為

其中,u(k) 為第k級的容許控制;x(k) 為當前狀態.利用動態規劃解路徑規劃問題,就是要找到決策序列u*(k),使得代價函數

達到最小.

本文將RRT 森林算法搜索到的路徑節點作為容許控制集,通過動態規劃確定在容許控制集中最優的決策序列,從而刪除其余的冗余點,實現對多無人機路徑的優化.

3.2 刪除冗余點和路徑優化

根據三角不等式,任取不共線的三點A,B,C,則三點之間相互連接的線段長度,必然滿足

當且僅當A,B,C共線時,有

RRT 森林算法搜索產生的較曲折的路徑,可以利用上述原理優化.然而,盲目刪除冗余點,未必能得到最優路徑.因此,本文提出基于動態規劃的冗余點移除方法.

定義兩點間指標函數

對于第i條原路徑Pi,將起點到終點之間每一個點獨立作為一級,對每一級計算指標函數,并記錄指標函數極小的上一節點索引.計算完畢后,從終點根據上一節點的索引往前查找,即得優化后的路徑索引序列.根據索引序列查找Pi中對應點的坐標,即得優化后的路徑.動態規劃移除冗余點的偽代碼見算法3.

算法 3.動態規劃移除冗余點

第一次動態規劃是為RRT 森林算法生成的路徑刪除冗余點,優化后的路徑顯著縮短,但仍由原路徑的部分節點連接而成,易出現不必要的繞行以及路徑節點重疊,這需要進一步優化.而經過第一次動態規劃所得的路徑,節點比較稀疏,需要對路徑進行插值處理,得到節點較密集的路徑用于第二次動態規劃.

對于路徑Pi,經過第一次動態規劃共有ni個航段,可擬合成一個分段函數,但由于路徑中x與y不能唯一映射,故采取從起點到該點的里程lj為參數,其中j=1,2,···,ni,將路徑按參數方程的形式擬合成x(l) 與y(l) 如下:

按一定步長 Δl取參數l,代入式(10)和式(11)中分別求得對應的x坐標和y坐標,即得到插值后的路徑.

對于經過插值處理后的路徑,再一次進行動態規劃,即可裁去中不合理的轉角,并解決絕大部分的路徑重合問題.

注 3.在實際高層消防任務中進行路徑規劃時,所取步長 Δl不宜過短,否則會引發動態規劃的維數災難,導致規劃時間過長,無法及時對路徑進行重規劃.

4 仿真研究

本節對上述基于RRT 森林算法的路徑規劃方法進行仿真研究.根據障礙物的復雜程度以及高層消防任務所面臨的實際環境可分為復雜環境和實際簡單環境.復雜環境以迷宮作為地圖,實際環境以實際高層住宅平面圖作為地圖.又根據路徑規劃的起點和終點組合的數量,分為單一路徑規劃和多路徑協同規劃.其中,單一路徑規劃主要以復雜環境下路徑規劃為主;而多路徑規劃是在實際環境中進行3 架無人機飛越5 個航段的協同路徑規劃.

仿真研究共分為三部分: 1)對RRT 森林算法與基本RRT 算法、雙向RRT 算法在復雜環境下的搜索效率進行對比,并給出多起點多終點路徑規劃表現;2)對比RRT 森林算法生成的路徑經過各次動態規劃優化后的效果;3) RRT 森林算法使用改進和未改進的障礙物接近檢測的對比效果.

在仿真圖中,加粗的黑色線條表示結果路徑,通過不同的線型區分多路徑,淺色細實線表示RRT 森林算法產生的隨機樹枝干.圓點為起點,五角星為終點,若兩者重疊,則表示給定的中途點.

4.1 RRT 森林算法與其他RRT 算法搜索效率比較

為了測試RRT 森林算法的路徑規劃效率,本文對不同隨機樹數量的RRT 森林算法與基本RRT 和雙向RRT 在復雜環境下進行比較.其中,隨機樹數量取NTree=1,2,5,10,20,50,隨機樹數量為1 時算法相當于基本RRT,為2 時相當于雙向RRT,其余為RRT 森林算法,其他參數保持一致.考慮到RRT 算法的固有隨機性,對各種算法分別進行不少于1 000 次實驗,通過箱形圖展示測試結果.

圖7 展示了基本RRT 算法、雙向RRT 算法以及NTree=30 的RRT 森林算法在復雜環境中的表現.從圖7(a)和圖7(b)可見,基本RRT 以及雙向RRT 都產生了較多的無效點,且集中在隨機樹的根節點附近,表明搜索被局限在隨機樹現有節點附近.而從圖7(c)中可見,RRT 森林算法則產生較少的無效點,且采點比較均勻.在可行區域內的圓點,表示中間隨機樹初始根節點.這些從隨機點開始搜索的樹,從搜索初期就拓寬了RRT 森林算法的搜索范圍,提升了搜索的廣度,避免了RRT 算法搜索局限在某個范圍內,減少了無效搜索,從而提升了在復雜環境中的搜索效率.

圖7 各算法在復雜環境下的運行結果Fig.7 Performance of algorithms in complex environment

圖8 用箱形圖展示不同隨機樹數量的RRT 森林算法及基本RRT 算法、雙向RRT 算法的實驗數據分布情況.表1 則揭示了圖8(a)中箱形圖的數據.由表1 結合圖8(a)分析可得,基本RRT 算法在復雜環境下的搜索時間中位數為8.00 s,雙向RRT 算法為2.57 s,而RRT 森林算法中,搜索時間與隨機樹的數量呈先顯著下降,再略微增加的趨勢,當NTree=20 時,搜索時間的中位數為0.48 s,與基本RRT 算法相比,節約了94%的搜索時間.另外,根據每種算法的上四分位數與下四分位數之差,可得搜索時間的穩定性與隨機樹數量呈正相關.從圖8(b)可知,路徑搜索所使用的迭代次數隨著隨機樹數量的增加而減少.從圖8(c)可知,生成路徑的路徑點數隨著隨機樹的增多先減少后增加.上述實驗數據表明,在RRT 森林算法的運用中,為避免路徑過于復雜,以及不必要的運算開銷,需要視環境復雜程度選擇合適的隨機樹數量.

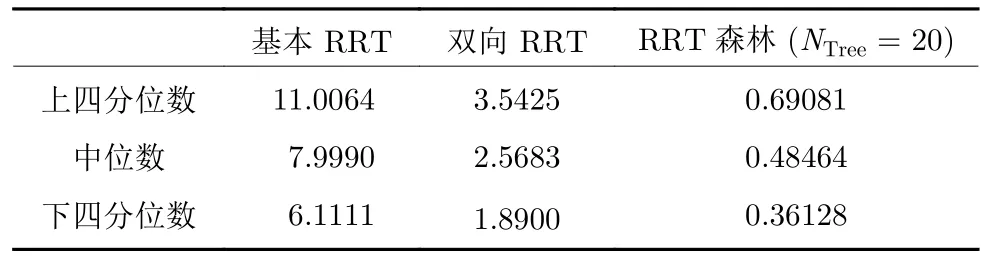
表1 各算法搜索用時數據(s)Table 1 Statistics of time used in exploring of each algorithm (s)

圖8 各算法在復雜環境中的實驗數據Fig.8 Statistics among algorithms in complex environment

注 4.圖8 和表1 所述的搜索用時數據,包括取隨機根節點的時間和路徑搜索時間,不包括動態規劃的運算時間.

RRT 森林算法基于多個隨機樹連接與合并,可支持多路徑規劃,因此可用于多無人機協同路徑規劃.圖9 為RRT 森林算法多路徑規劃的表現.

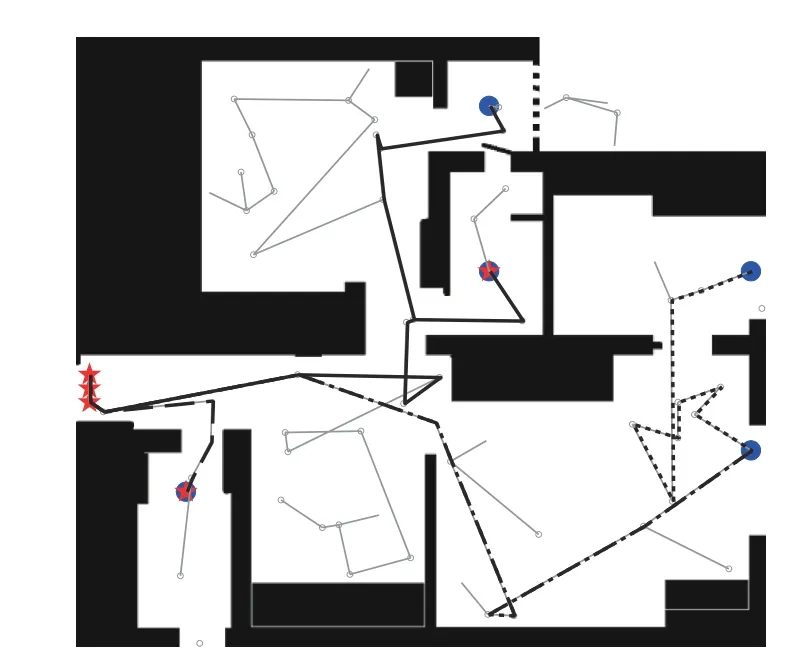
圖9 RRT 森林算法多路徑規劃Fig.9 Multi-path planning by RRT-forest

從圖9 中可見,RRT 森林算法通過將多隨機樹連接合并,達到同時兼顧多起點多終點的路徑規劃目標,最終達到所有起點和終點都被包含在同一個隨機樹上,此時只需按照起點與終點的組合尋找路徑即可.值得注意的是,這些路徑之間往往都存在公共線段,且這些路徑比較曲折,甚至有不必要的繞行,因此無法直接應用于高層消防無人機協同任務當中,需要進行刪除冗余點等路徑優化處理.

4.2 基于動態規劃的路徑優化

為了測試動態規劃對路徑的優化效果,本文分別針對復雜環境下的單路徑和實際環境下的多路徑進行優化處理.

由圖10(a)可知,未經處理的路徑非常曲折,且存在冗余點.對路徑進行第一次動態規劃得到圖10(b),發現許多折線被拉直.顯然,從起點到終點的路程已被縮短,但仍然存在不合理的轉角.將第一次動態規劃的結果進行參數方程擬合并重新采樣,再次進行動態規劃,得到圖10(c).由圖10(c)可見,在轉角處能夠緊貼障礙物邊緣,以取得最短的路徑.

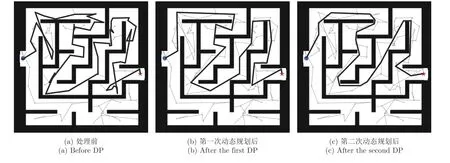
圖10 單路徑優化過程Fig.10 Optimization of single path

針對多條路徑的優化效果,本文進行了實際環境下的多路徑優化實驗.假設3 架無人機以不同高度飛行,且飛行過程中保持高度不變.仿真結果如圖11 所示.由圖9 可發現,處理前的路徑非常曲折,且有路徑重疊的現象.進行第一次動態規劃后的效果如圖11(a)所示,由圖可見,許多不合理的轉角被移除,但仍然存在個別交叉與重疊,部分轉角仍然過大.在圖11(b)中,對各條路徑進行擬合并重新采樣后,再次進行動態規劃,并且按照任務設定將應合并的路徑合并.由圖可見,5 條路徑被合并成3條路徑并完全分開,各段路徑筆直且不存在交點,而重疊的路徑僅存在于同一無人機飛往與飛離中途點的路徑中.

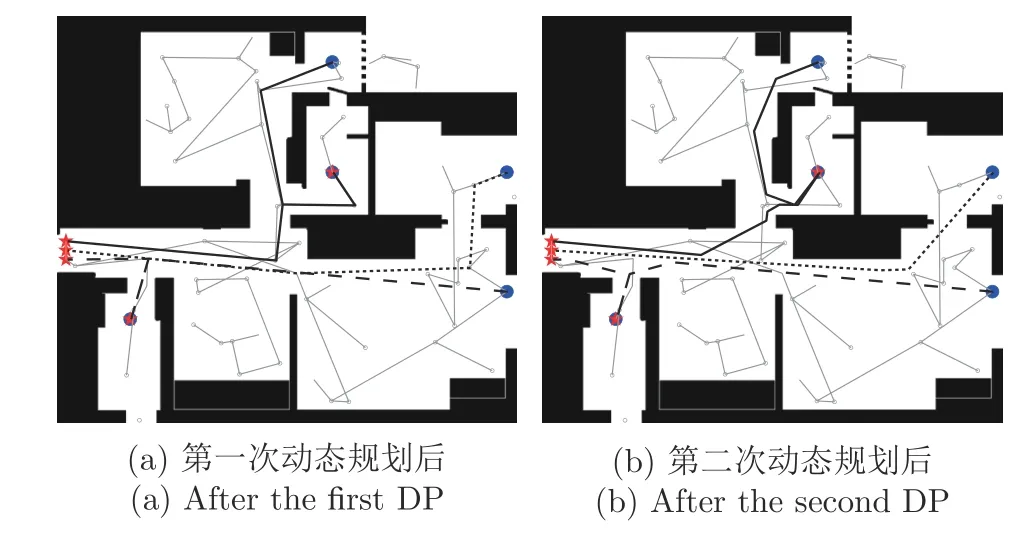
圖11 多路徑優化過程Fig.11 Optimization of multi-paths

4.3 障礙物接近檢測改進

從圖10 可知,經過兩次動態規劃得到的路徑,部分線段是緊貼障礙物的,在多無人機執行高層消防救援任務時,這樣的路徑可行性仍然較差,因此需要在路徑搜索以及動態規劃中,使用改進的障礙物接近檢測代替原碰撞檢測,實現使路徑與障礙物保持一定距離的目標.對此,本文對障礙物接近檢測與原碰撞檢測進行了對比實驗.

注 5.對于迷宮地圖,假設無人機直徑rUAV≤20 cm;對于實際高層建筑地圖,圖上1 個像素代表10 mm,假設無人機直徑rUAV≤30 cm,并為每架無人機分配不同的飛行高度,在飛行中高度將保持不變.

從圖12(a)可見,RRT 森林算法以及動態規劃中使用未改進的碰撞檢測函數時,得到的路徑與障礙物的最小距離為0,這意味著無人機執行這樣的路徑會與障礙物發生剮蹭.而從圖12(b)可見,使用改進的障礙物接近檢測后,設置安全距離為10 cm,得到的路徑與障礙物的距離顯著大于使用原碰撞檢測的算法所生成的路徑.圖12(b)也給出了使用改進障礙物接近檢測方法的RRT 森林算法所得路徑與障礙物的最短距離曲線,可知路徑到障礙物最小距離均大于給定安全距離10 cm.可見,改進的碰撞檢測方法顯著提高了路徑的可行性,使得RRT森林算法在未經膨脹處理的地圖中,通過設置安全距離進行路徑規劃可以得到更可行的路徑.

需要注意的是,當安全距離設置過大時會影響路徑搜索效率,導致搜索失敗率增加,搜索時間變長,因此需要合理設置安全距離.在高層建筑室內,對于無人機仍有比較大的空間,此時可以設置更大的安全裕度.圖13 為一般室內環境下,安全距離為15 cm 的規劃結果及其與障礙物之間的距離曲線,此時總規劃時間大約為1 s.而對于圖12 中的復雜環境,由于空間狹小,當安全距離取10 cm 時會使得可行區域大幅減少,隨機樹生長成功率降低,規劃時間會超過2 s.

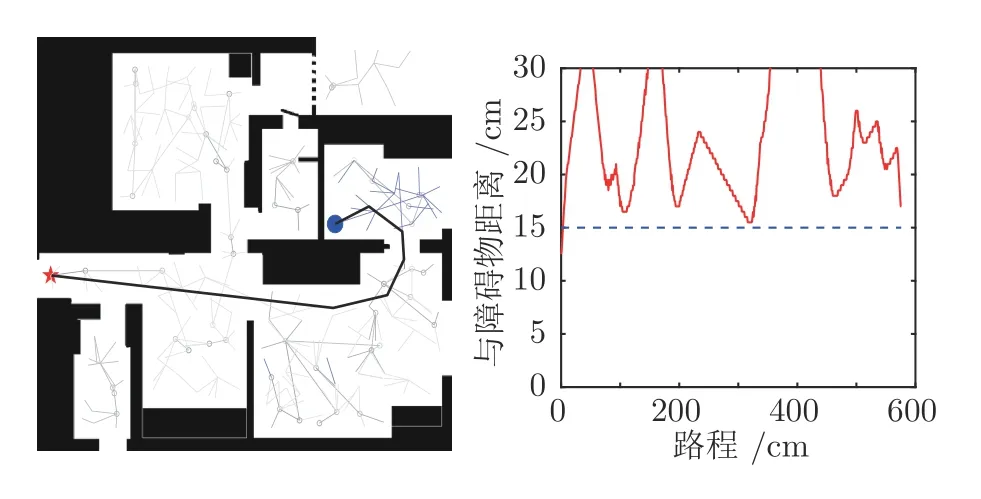
圖13 實際環境下改進碰撞檢測效果Fig.13 Result of novel obstacle checking in practical environment

5 結束語

考慮到多無人機協同執行高層室內消防救援任務時的高度緊迫性,在路徑規劃方面本文提出RRT森林算法,提高了路徑搜索的速度以及結果可行性.通過在RRT 算法中增加中間樹,解決了RRT 算法在前期搜索范圍受限的問題,提高了復雜環境下的路徑搜索效率、搜索速度及魯棒性,并且為多無人機進行協同路徑規劃提供了重要支撐.通過設計新型碰撞檢測算法,使得路徑與障礙物始終保持安全距離.應用兩次動態規劃和參數方程擬合方法,移除了路徑上的冗余節點,增強了規劃結果的實用性.實驗結果表明,RRT 森林算法可實現復雜環境下快速規劃多條安全可行的路徑,并能滿足高層消防救援中路徑頻繁重規劃的需求.

關于高層消防多無人機室內協同路徑規劃,本文提出的RRT 森林算法能在較短時間內得到可行性較高的路徑,但在無人機數量較多、任務分配復雜的情況下,在協同能力方面仍有提升空間.因此將來的工作可以致力于提高多無人機協同路徑規劃的能力.