高速鐵路運營期沉降后擬合調整縱斷面曲線參數

臧傳臻

中國鐵路設計集團有限公司， 天津 300308

我國高速鐵路部分線路途經深厚軟土地帶，區域內沉降具有不均勻、范圍大、一定時期內持續等特點，再加上持續多年的高頻次運營使用，部分地段的線路偏差超出了TB 10621—2014《高速鐵路設計規范》和TG/GW 115—2023《高速鐵路線路維修規則》的限值要求。此外，我國有大量無砟軌道線路，線形調整量較大時需進行揭板重建，實施困難且工作量大。因此，有必要對超限地段進行平縱斷面線形重構，并進行動力學仿真評估，從而在確保行車及下部結構安全性、乘車舒適性的前提下，減少工程投資，為運營期高速鐵路基礎設施沉降的高效整治提供理論依據。

通過增設豎緩和曲線來優化高速鐵路縱斷面線形的意義顯著。一方面，隨著高速鐵路運營速度越來越高，列車與線路之間的動力相互作用顯著增大，高速列車具有較長的振動衰減周期，易發生振動疊加。相比于平面線路同時采用緩和曲線與圓曲線進行過渡，傳統縱斷面線路只以圓形豎曲線連接兩坡段，線路在直圓點和圓直點處會出現曲率突變，從而導致車體垂向加速度產生突變，致使列車受到垂向沖擊。通過在圓形豎曲線與直線坡段之間設置豎緩和曲線，可避免曲率突變，從而提升高速鐵路縱斷面線形的平順性，增強列車運行安全性和舒適性。另一方面，運營期內發生工程沉降變形后，對于沉降變形范圍較大但差異沉降變化速率較小的地段，在扣件可調范圍之內可采用扣件調整方案。為了確保擬合調整曲線更接近實際不均勻沉降曲線，減小軌道結構調整量，在進行縱斷面線形重構時可在縱坡與豎圓曲線之間設置豎緩和曲線。

國內外相關學者目前對傳統縱斷面線形參數做了較多研究。Hodas［1］分析了不同速度條件下縱斷面參數對車輛振動的影響。魏云鵬［2］對比分析了不同縱斷面參數對客貨共線鐵路列車動力響應的影響。帥文忠［3］基于實測軌面高程數據，從動力學角度對普速鐵路既有線縱斷面幾何優化進行了研究。易思蓉等［4］研究確定了客貨共線鐵路不同的隧道長度所對應的最大坡度系數。張夢然［5］對不同縱斷面、不同牽引制動工況條件下重載列車動力學性能和運行能耗進行了研究。王佳［6］研究了不同牽引制動工況下最小坡段長度對列車縱向作用力的影響。汪瑩［7］分析了不同牽引制動工況下坡度同重載鐵路列車行車性能的關系。魏慶朝等［8］研究了縱斷面線路參數和車速對行車動力響應指標的影響規律。國外研究成果對縱斷面參數的研究包含了坡度、坡段長度、豎曲線半徑、車速等方面，對縱斷面內豎緩和曲線的相關研究極少。

本文針對車輛在縱斷面曲線上行駛建立數學分析模型，對比兩種豎緩和曲線的數學特性和動力學特性，并基于此提出列車行駛速度、列車牽引加速度、豎曲線半徑、豎緩和曲線長與運動加速度、加速度時變率之間的關系式；借鑒350 km/h 及以下車速條件下考慮線路參數所進行的動力學響應變量計算思路，并在縱斷面中增加豎緩和曲線因素，建立CRH380B 列車-軌道動力學模型，仿真計算列車行車動力響應變量，驗證豎緩和曲線參數取值的合理性。在已知列車運行工況的情況下，研究成果可為縱斷面線路參數的合理取值提供借鑒。

1 豎緩和曲線函數

規定變坡點為坐標系原點，且線路上某坐標點與變坡點的里程差和高程差分別為該坐標點的x、y值。如果連續函數存在n階連續導函數，則稱其Cn連續。傳統鐵路縱斷面線路通過在相鄰坡段間設置豎曲線，只能實現C1連續。基于行駛動力學理論將列車簡化成一個質點，則質點在縱斷面某位置所受的離心力和離心加速度均與線路函數在該位置的二階導數（曲率）有關，所受離心力變化率和離心加速度變化率與三階導數（曲率變化率）有關。故若使列車在行駛過程中所受離心加速度連續變化，線路函數應滿足C2連續；若使列車在行駛過程中所受離心加速度變化率連續變化，線路函數應滿足C3連續。本文將線路設置成直坡段 + 豎緩和曲線 + 圓形豎曲線 + 豎緩和曲線 +直坡段的形式，使線路實現高階單調連續可導。

豎緩和曲線采用多項式函數。計算表明，可實現線路C2連續的最低次方多項式函數為三次多項式函數，規定為第一類豎緩和曲線線形。對于直坡段、豎緩和曲線段、圓形豎曲線段，線路函數依次表達為

式中：g1為直坡段坡度角，以順時針為正，rad；LH為豎緩和曲線的長度，m；LY為圓形豎曲線的長度，m；ρ為曲率，m-1，豎曲線為凹形時取1/R，為凸形時取-1/R，R為曲線半徑。

經推導知，可實現線路C3連續的最低次方多項式函數為五次多項式函數，規定為第二類豎緩和曲線線形。對于豎緩和曲線段、圓形豎曲線段，線路函數依次表達為

對比式（2）和式（4）、式（3）和式（5），發現C3連續曲線與C2連續曲線的最大豎向差值為/60，可見豎曲線半徑越小，豎緩和曲線越長，則豎向差值越大。

2 線路參數合理取值

車輛在縱斷面曲線上的運動加速度、加速度時變率可作為確定線路參數的主要評價指標。通過建立列車行駛速度、列車牽引加速度、豎曲線半徑、豎緩和曲線長與評價指標之間的關系式，進而根據評價指標限值來確定線路參數限值，實現線路設計參數匹配。

因為縱斷面坡度很小，所以列車通過兩坡段間夾曲線時所受未被平衡離心加速度可簡化為

式中：ay(x)為列車在x位置處的豎向加速度，m/s2；v(x)為列車在x位置的行駛速度，m/s；ρV(x)為線路在x位置的曲率，m-1。

當列車處于圓形豎曲線上時線路曲率最大，故而最小豎曲線半徑可由式（7）確定。

式中：ay為列車豎向離心加速度最大值，m/s2；vmax為列車最高行駛速度，m/s；ash為豎向離心加速度容許值，國外一般取0.15 ～ 0.60 m/s2。

鐵路行業規定，豎向加速度時變率容許值（a′sh）一般取0.3 ～ 0.5 m/s3，又v(x) = dx/dt，因此應滿足

式中：a′y(x)為列車在x位置的豎向加速度時變率，m/s3；ax(x)為列車在x位置的縱向加速度，m/s2；y(x)為列車在x位置的豎向位移，m。

由式（8）可知，在特定圓形豎曲線和豎緩和曲線上，列車行駛速度和縱向加速度越大，所受豎向加速度時變率越大。第一類豎緩和曲線的最大曲率為|ρ|，曲率變化率為固定值|ρ|/LH；第二類豎緩和曲線的最大曲率變化率達最大值1.5|ρ|/LH時的曲率為|ρ|/2。故兩類豎緩和曲線在滿足式（7）的同時，還應分別滿足式（9）、式（10）。由列車最高行駛速度、最大牽引加速度、最小豎曲線半徑、加速度時變率限值，可確定最小豎緩和曲線長。

式中：a′y為列車豎向離心加速度時變率最大值，m/s3；amax為列車最高牽引加速度，m/s2。

可知，amax和vmax越大、a′sh和R越小，LH可取的最小值越大。令ash= 0.38 m/s2，vmax= 350 km/h，則R取25 000 m。令amax= 0.2 m/s2，a′sh= 0.5 m/s3，則第一類豎緩和曲線的LH最小值為106 m（不考慮縱向加速度時為74 m），第二類豎緩和曲線的LH最小值為130 m（不考慮縱向加速度時為111 m）。建議優先采用第二類豎緩和曲線，困難地段可采用第一類豎緩和曲線。

3 仿真模型

基于多剛體動力學理論、結構動力學理論，采用動力學仿真軟件和有限元軟件，建立列車-線路-軌道耦合動力學模型。令車體、每個轉向架、每個輪對各有5 個自由度（橫移、沉浮、側滾、搖頭、點頭），從而得到一個具有35 個自由度的橫向-垂向耦合的車輛模型。無砟軌道的振動形態主要表現為鋼軌和軌道板在垂向和橫向的變形。鋼軌在垂向和橫向均視為連續彈性點支承的無限長梁。軌道板與下部混凝土基礎呈連續彈性點接觸狀態，且軌道板的長寬尺寸遠大于其厚度，因而在垂向將軌道板簡化為彈性薄板，其變形主要體現為垂向的位移、彎曲和翹曲，在橫向上軌道板的變形主要為板的彎曲。輪軌法向力由赫茲非線性彈性接觸理論確定，輪軌蠕滑力由經Johnson-Vermeulen理論進行修正過的Kalker理論確定。

采用某高速鐵路區段2 000 m 列車檢測數據，輸入其高低與軌向不平順（圖1），進行模型驗證。結合列車實測數據，從時頻域對比車體垂向、橫向加速度的仿真與實測數據，驗證模型的正確性，見圖2。可知：車體垂向、橫向加速度的仿真結果與實測數據在時域和頻域上均能得到較好的對應，即仿真結果與實測數據有較好的相關性。本文所建立的列車-線路-軌道耦合動力學模型合理。

圖1 實測軌道不平順

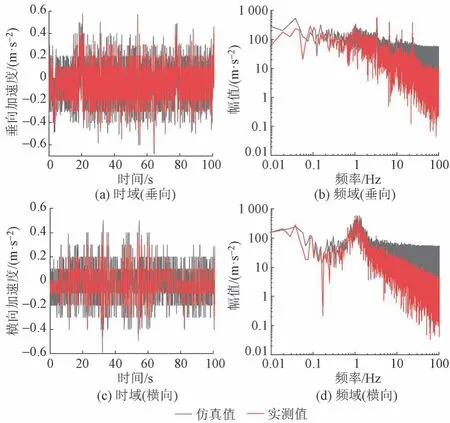
圖2 車體垂向、橫向加速度時頻域對比

4 工程案例

根據某工程案例沉降情況，確定整治方案為：根據既有軌面高程，通過扣件調整，達到擬合豎曲線方式設計適應速度350 km/h 的新線形。其中擬合豎曲線半徑不小于25 000 m，五次拋物線型豎緩和曲線的長度不小于130 m，扣件豎向調整量應滿足-4 ～ 26 mm的要求。

4.1 軌面豎曲線擬合

根據既有軌面高程差數據（扣件均為標準件時的高程數據），按350 km/h 的運行速度，對軌面高程差進行豎曲線擬合，平順性優化前后的軌道垂向偏差見圖3，調整量見圖4。調整量在-2 ～ 8 mm。

圖3 平順性優化前后軌面垂向偏差

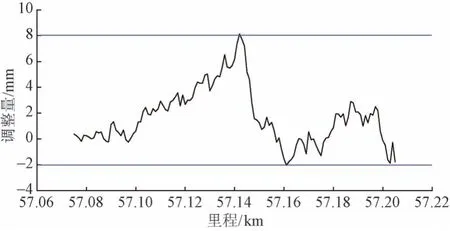
圖4 扣件調整量

平順性優化前后10、30、60 m 中點弦測值見圖5。可知：三種中點弦測值均有不同程度改善，且滿足高低不平順控制要求。

4.2 動力學仿真評估

對新設計軌面目標線形開展行車安全性和舒適性評估。行車舒適性指標主要包括車體垂向、橫向加速度，安全性指標主要包括輪軌垂向力、輪軌橫向力、脫軌系數和輪重減載率。

計算得到速度350 km/h 條件下沉降整治區段及其相鄰區段共計530 m 范圍內的各動力學響應指標時程曲線，見圖6。各動力響應指標的最大值見表1。可知：行車舒適性指標中的車體垂向加速度，安全性指標中的輪軌垂向力、脫軌系數、輪重減載率均滿足限值要求，且線形優化后分別減小54.47%、24.54%、87.69%、93.65%。可見，高速動車組能安全舒適地以設計速度350 km/h 通過該新設計軌面目標線形地段，目標線形可進行實施。

表1 優化前后各動力響應指標最大值

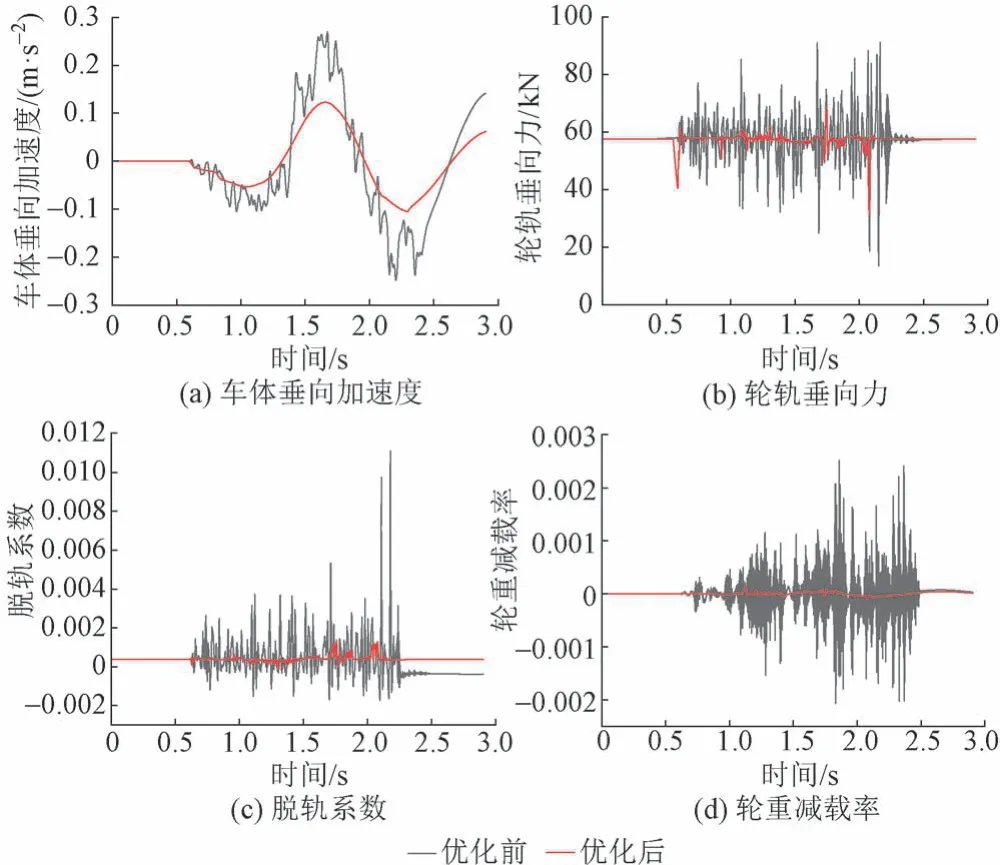
圖6 優化前后各動力學響應指標的時程曲線

5 結論

1）豎曲線半徑越小，豎緩和曲線越長，則兩類豎緩和曲線的豎向差值越大。

2）根據提出的列車運行工況、線路參數、舒適度指標之間的關系式，在已知列車最高行駛速度和最大牽引加速度的情況下，可確定最小豎曲線半徑和最小豎緩和曲線長，為運營期沉降變形后高速鐵路線路擬合調整方案的制定提供理論依據。

3）列車最高行駛速度和最大牽引加速度越大，或者加速度時變率限值和豎曲線半徑越小，則最小豎緩和曲線長度越大，車速350 km/h 條件下的三次拋物線和五次拋物線線形中緩和曲線的最小長度分別為106、130 m。