高中生數學抽象能力現狀調查及生成路徑探析

宋召靜 金晶

摘要：以學生函數學習的外在表現行為為載體，對H市某高中學生的數學抽象能力進行測評研究.結果表明：高中生數學抽象能力處于中等水平且學生之間差異較大；數學抽象能力水平受性別因素影響較小；學生的數學學業成績、數學學習興趣、數學學習策略與數學抽象能力水平之間具有正向相關性.最后，針對調查結果，提出培養高中生數學抽象能力的函數教學策略.

關鍵詞：高中生；函數學習；數學抽象能力；測評研究

數學抽象是指通過對數量關系與空間形式的抽象得到數學研究對象的素養.作為六大數學核心素養之首，數學抽象是數學的基本思想，是形成理性思維的基礎.文獻[3]中指出，在眾多數學關鍵能力中，數學抽象能力是數學學習基礎性的關鍵能力，是形成數學概念、構建數學模型、提升數學思想、完成命題推演的必備能力.函數教學是培養學生數學抽象能力的重要環節.因此，在函數相關教學中，教師要注重引導學生在熟悉的、關聯的和綜合的問題情境中抽象出一般規律和結構，從函數圖象中抽象出符號化的語言，利用通性通法解決數學問題，以促進學生數學抽象能力的有效提升.

為客觀了解現階段高中生數學抽象能力情況，筆者對H市某高中學生的數學抽象能力進行了調查研究，并針對學生現狀提出了一些具體的函數教學策略.

一、研究設計

1.研究對象

本研究選擇H市某高中的高二學生作為研究對象，他們已經學習了人教A版《普通高中教科書·數學》必修部分“函數”相關的內容.本次調查以問卷的形式展開，共在四個班級（兩個實驗班、兩個普通班）發放160份問卷，回收有效測評問卷148份，占比92.5%，調查結果有效.

2.研究工具

本研究借鑒文獻[3]對于數學抽象能力的三級水平的劃分（歸納與釋義水平、關聯與建構水平、拓展與普適水平），將其作為數學抽象能力測量框架.問卷中的測試題主要選自《〈普通高中數學課程標準（2017年版2020年修訂）〉解讀》中的案例和云南師范大學凡丹設計的關于數學抽象水平研究的測試卷，測試題的選取既考慮了學生認知發展的階段性和順序性，又考慮了教師教學的任務安排進度，共計4道題目，滿分51分.規定學生得分率在10% ～ 40%之間達到歸納與釋義水平、40% ～ 70%之間達到關聯與建構水平、70%以上達到拓展與普適水平.調查問卷主要借鑒文獻[5]中編制的量表，共計15道題目.其中，第1題和第2題為學生的基本信息統計，包括性別和平時的數學學業成績；第3 ～ 8題調查學生的數學學習興趣；第9 ～ 15題調查學生的學習策略.

二、研究結果統計與分析

本調查旨在分析當前高中生數學抽象能力的整體情況，主要包括性別對學生的數學抽象能力有無影響，以及學生的數學學業成績、數學學習興趣、數學學習策略與抽象能力水平的相關關系.在研究這些問題之前，從以下方面對問卷內容的可靠性進行分析.

1.信度和效度分析

除去基本信息，對148份調查問卷中學生所得分數進行信度分析，利用SPSS軟件可靠性分析，采用信度系數的一致性檢驗，發現Cronbachs Alpha為0.866 > 0.70，屬于可以接受的范圍，具有良好的信度，說明問卷結果具有較強的可靠性.

對問卷中四道測試題的效度進行分析，采用KMO和Bartlett檢驗，得到KMO值為0.772 > 0.60，顯著性為0.000 < 0.05，表明該數據適合做因子分析，說明題目之間具有一定的關聯性，題目的效度良好，能夠較好地反映高中生數學抽象能力的現狀.

2.高中生數學抽象能力的整體情況分析

本文選擇柯爾莫哥洛夫-斯米諾夫（KolmogorovSmimiov）檢驗來確定學生的數學抽象能力總體表現得分是否滿足一致性.由表1可知，Sig. = 0.059 > 0.05，表明學生抽象能力整體表現得分呈正態分布，并在如圖1所示的Q-Q圖中看到大多數點分布在直線附近，表明學生的數學抽象能力表現得分服從正態分布.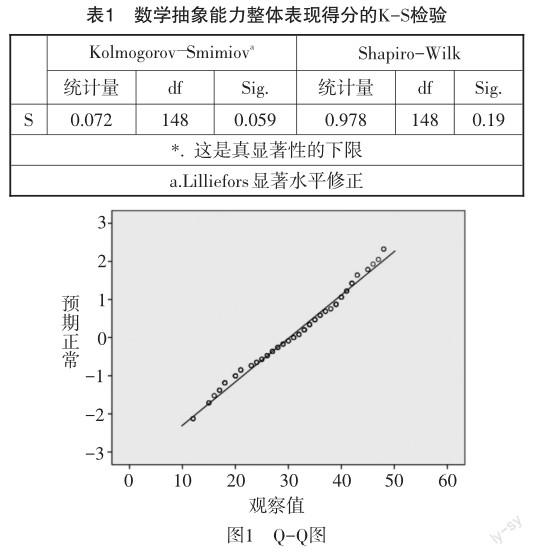

對于測試卷中的四道題目，被試的最高得分為48分，最低得分為12分，相差36分，說明學生之間數學抽象能力整體得分差距比較明顯；被試總體平均分為30.18分，得分率為59.18%，說明高中生數學抽象能力整體處于中等水平.

按照數學抽象能力評分標準，統計處于歸納與釋義水平、關聯與建構水平、拓展與普適水平的人數，發現有29.73%的學生（44人）數學抽象能力處于歸納與釋義水平，這部分學生存在對公式符號混亂使用的情況，教師要因材施教，提高學生的數學抽象能力.有60.81%的學生（90人）達到關聯與建構水平，這部分學生能選擇適切的數學語言表達數學問題情境中的數量關系和圖形關系，理解數學概念的內涵并建構知識之間的聯系.高中函數知識具有完整的邏輯體系，對于這部分學生而言，在理解的基礎上建構函數知識之間的聯系，將數學命題推廣到一般形式，并選擇恰當的數學符號語言進行表達是進行數學抽象的關鍵.僅有9.46%的學生（14人）達到了拓展與普適水平，這些學生能夠創造性表征問題中的數量關系，利用通性通法解決數學問題.通過測試發現，大部分學生不能較好地處理難度較大的綜合性問題，較為典型的是學生難以解決數學建模類問題，說明學生的創新能力不足.

3.差異性分析

在本次調查的148名被試中，包含71名男生和77名女生，采用獨立樣本T檢驗來分析性別對于數學抽象能力是否有顯著影響，數據檢驗結果如圖2所示.可以直觀地看到，男生和女生在數學抽象能力三個水平上的整體差異較小.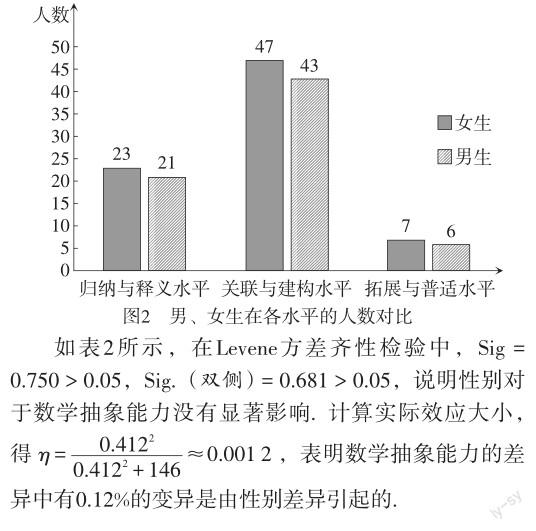

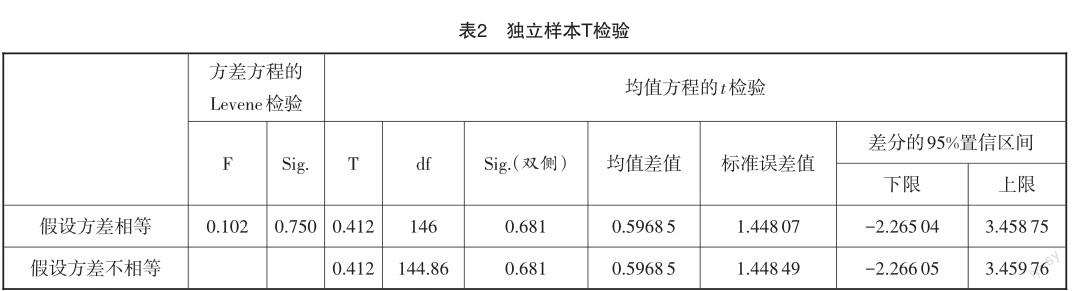
綜上所述，高中生的數學抽象能力水平幾乎不受性別因素影響，即學生在函數學習中數學抽象能力的高低與性別的相關性不顯著.

4.相關性分析

在了解學生數學抽象能力水平的基礎上，繼續探討影響學生數學抽象能力的因素，分別將學生的數學學業成績、數學學習興趣、數學學習策略與數學抽象能力進行相關性分析，得到結果如表3所示.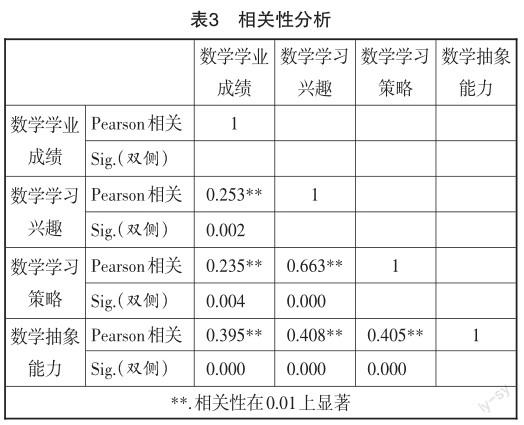

表3的數據檢驗結果表明，數學學業成績與數學抽象能力的相關系數r = 0.395** > 0，P = 0.000 < 0.01，說明數學學業成績與數學抽象能力之間存在顯性的正相關關系，即數學學業成績越好，數學抽象能力越強；數學學習興趣與數學抽象能力的相關系數r = 0.408** > 0，P = 0.000 < 0.01，說明數學學習興趣與數學抽象能力之間存在顯性的正相關關系，即數學學習興趣越高，數學抽象能力越強；數學學習策略與數學抽象能力的相關系數r = 0.405** > 0，P = 0.000 < 0.01，說明數學學習策略與數學抽象能力之間存在顯性的正相關關系，即數學學習策略越優化，數學抽象能力越強.

三、研究結論

通過數據分析，總結高中生數學抽象能力現狀如下.

（1）高中生的數學抽象能力整體處于中等水平，且學生個體間的數學抽象能力差異較大，教師在教學過程中還需要進一步發展學生的數學抽象能力.

（2）高中生的數學抽象能力水平幾乎不受性別因素影響，即男生和女生之間的數學抽象能力并無明顯差異.

（3）高中生的數學學業成績、數學學習興趣和數學學習策略與數學抽象能力之間均呈現較強的正相關.

四、函數教學中生成數學抽象能力的路徑

數學抽象能力對學生理論知識的掌握和應用能力的發展都有著不可忽視的影響，而函數相關內容的學習是培養學生數學抽象能力的關鍵.對此，筆者基于調查結果，從教師的教和學生的學兩個方面，提出關于函數教學的一些建議，以期提高學生的數學抽象能力.

1.引導學生獨立思考，鍛煉學生的抽象思維

由調查結果可知，當前高中生的數學抽象能力整體處于中等水平.對此，在有關函數內容的教學中，教師要有目的地引導學生獨立思考，不斷尋找新、舊知識的連接點，使教學建立在學生通過一定的努力和思考可以達到要求的知識水平，從而全面發展學生的抽象思維.此外，針對學生個體之間數學抽象能力差異較大的現狀，教師要針對不同層次的學生精心設計不同形式的教學活動，以促進學生抽象能力的提高.例如，在“函數的單調性的概念”的教學中，若直接給出教材中的定義，學生會感覺很抽象，難以理解.對此，教師要讓知識生動起來，讓學生學會數學語言的轉化，熟悉符號語言的表達方法，進而給出嚴格的數學表達，鍛煉學生的抽象思維.

2.創設新穎的教學情境，直擊函數知識本質

調查結果顯示，數學學習興趣越高的學生數學抽象能力越強.因此，教師可以通過創設新穎、有趣的教學情境，提升學生對即將學習的數學知識的研究興趣，進而更容易接受并內化所學知識.教師在創設概念教學情境時，需要考慮學生已有的認知水平、知識背景，以及所創設的情境與函數知識本質之間聯系的緊密性，從而有效激發學生的認知沖突，讓學生產生學習的欲望，進而主動去探索、去發現，并在這個過程中發展數學抽象能力.

3.夯實理論學習基礎，形成系統知識框架

學會構建知識之間的關聯性，有序構建函數知識體系是提升學生抽象能力的一個關鍵的數學學習策略.學生理論基礎越扎實、知識框架越清晰，其數學抽象的過程就會越順利.高中函數知識具有高度的邏輯性和順序性，知識之間又相互聯系.在函數內容的教學過程中，教師要注重學生對基本概念的掌握，不僅要幫助學生理解有關的概念、定理和法則，還要促使學生理解有關概念的內涵和外延，引導學生對知識整體把握.因此，在保證學生了解、掌握有關基礎知識和基本技能的基礎上，教師要更加注重培養學生對函數知識融會貫通的能力，幫助學生建立自身的數學知識體系，歸納解決同類問題的數學思想方法，為抽象綜合性問題打好思維基礎，促進學生數學抽象能力的形成與提升.

4.融合信息技術，助力學生抽象過程

高中階段主要以動態的方式刻畫函數，這對學生的抽象能力提出了更高的要求.對此，教師要仔細鉆研教材，采用多種教學形式，恰當地將信息技術融入函數教學中，以直觀、動態的形式生成知識，化抽象為具體，讓學生有效參與知識抽象的全過程.例如，在“指數函數的圖象和性質”的教學活動中，教師可以利用信息技術精準地呈現多個函數圖象，以便于學生的直觀觀察，進而歸納出指數函數圖象的兩種變化趨勢，并在此基礎上分類討論指數函數的性質，歸納其共同特征，最終抽象出指數函數的性質.

五、結束語

數學的抽象性是客觀存在的，并且隨著知識的拓展其抽象程度也在不斷提高.在函數教學中，教師要把握內容特點，找到數學抽象、函數知識和學生學習能力之間的契合點，以有效促進學生抽象能力的提高.

參考文獻：

[1]中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）[M].北京：人民教育出版社，2020.

[2]郭民，史寧中，朱立明，等.高中生數學抽象能力發展水平劃分與基于水平劃分的調查研究[J].課程·教材·教法，2022，42（6）：124-131.

[3]史寧中.學科核心素養的培養與教學：以數學學科核心素養的培養為例[J].中小學管理，2017（1）：35-37.

[4]凡丹. K市高二學生數學抽象素養水平調查研究[D].昆明：云南師范大學，2020.

[5]沈藝.高中生數學抽象素養培養策略研究：以函數教學為例[D].南京：南京師范大學，2021.