軸向磁通永磁電機扁銅線交流銅耗的混合解析計算及抑制

武 岳 張志鋒

軸向磁通永磁電機扁銅線交流銅耗的混合解析計算及抑制

武 岳 張志鋒

（沈陽工業大學電氣工程學院 沈陽 110870）

軸向磁通永磁電機的扁銅線交流銅耗會嚴重影響電機性能，因此扁銅線交流銅耗的精確計算與抑制十分重要。采用三維瞬態場計算交流銅耗，雖然可以獲得精確的結果，但存在計算時間長和對計算機性能要求高的問題。為了權衡計算精度與計算時間，提出一種混合解析計算的方法。該方法將三維有限元與解析法相結合，可以考慮趨膚效應、鄰近效應和外部磁場對交流銅耗的影響。為了抑制交流銅耗，提出采用扁線立繞的導體排列方式。利用該方法對不同導體排列方式的交流銅耗和電機效率進行計算，并通過三維瞬態場有限元進行驗證。最后，對一臺60 kW的樣機進行實驗，實驗結果、有限元結果和混合解析計算結果基本吻合，驗證了混合解析計算的準確性和扁線立繞的有效性。

軸向磁通永磁電機 扁銅線 交流銅耗 混合解析計算 導體排列方式

0 引言

軸向磁通永磁電機具有功率密度高、體積小等優勢，適用于對電機性能和安裝空間有較高要求的領域，如航空航天、可再生能源、電動汽車等[1-4]。高功率密度軸向磁通永磁電機的電磁負荷和熱負荷都趨于極限，并且受到趨膚效應、鄰近效應和外部磁場的影響，導致繞組交流銅耗較大、溫升較高，將嚴重影響電機的性能和絕緣材料的壽命[5-8]。因此，需要對繞組交流銅耗進行精確的計算。

軸向磁通永磁電機的繞組交流銅耗適合采用三維有限元進行精確計算[9]。文獻[10]為了分析軸向磁通永磁電機利茲線繞組的交流銅耗，基于三維有限元提出了單根繞組等效建模法。文獻[11]基于簡化的導體三維模型計算了圓銅線繞組的交流銅耗。采用三維瞬態場有限元計算交流銅耗，雖然可以獲得精確的結果，但存在計算時間長和對計算機性能要求高的問題。為了權衡計算精度與計算時間，提出了混合解析法[12-13]。文獻[14]采用二維混合解析法計算交流銅耗，該方法僅對繞組截面的磁通密度進行采樣，雖然可以加快計算速度，但是無法考慮繞組端部效應，不適用于軸向磁通永磁電機。為解決此問題，文獻[15]中提出了三維混合解析法，但是該方法并不適用所有情況，其僅適用于交流銅耗主要由外部磁場引起的情況。

在高功率密度電機領域中，扁銅線因槽滿率高、散熱性能優異而被采用，但扁銅線具有更高的交流銅耗[16-18]。因此，需要對扁銅線繞組的交流銅耗進行抑制。在文獻[19-20]中通過優化轉子結構來降低繞組交流銅耗。而文獻[21]通過合理選擇扁銅線的匝數與并聯根數來降低交流銅耗，這些方法需要大量的時間來改變電機的設計方案。在文獻[22-23]中提出用導體換位法來抑制繞組交流銅耗。文獻[24]利用利茲線導體間充分換位的方式有效地抑制了繞組交流銅耗。文獻[25]分析了圓銅線的排布方式對交流銅耗的影響，實驗結果證明，將導體盡可能全部布置在槽底會減小交流銅耗。但是這種繞組排布方式會造成散熱困難，在高功率密度電機中會加速繞組絕緣材料老化，降低電機運行的可靠性。

綜上所述，為了平衡扁銅線交流銅耗的計算精度和計算時間，本文提出一種混合解析計算的方法。該方法將三維有限元與解析法相結合，可以考慮趨膚效應、鄰近效應和外部磁場對交流銅耗的影響。提出扁線立繞的導體排列方式來抑制交流銅耗，并通過混合解析計算與三維瞬態場有限元分析了不同導體排列方式對交流銅耗和效率的影響。最后，進行樣機實驗，驗證了混合解析計算方法的準確性和扁線立繞的有效性。

1 電機模型

本文對雙轉子單定子軸向磁通永磁電機進行研究，其結構如圖1所示。定子之間不存在軛部，這種結構可以減輕定子鐵心質量，提高電機的功率密度。同時還采用分數槽集中繞組，繞組纏繞在獨立的定子上，可以減小繞組端部長度，降低繞組銅耗。電機定子槽口漏磁較多，而此拓撲結構具有兩個槽口，會增加繞組的交流銅耗。

圖1 雙轉子單定子軸向磁通永磁電機

圖1中繞組是簡化的三維等效模型，采用此等效模型計算交流銅耗會產生很大的誤差。因此，為了準確地計算交流銅耗，根據繞組實際尺寸，建立詳細的繞組模型。

扁銅線具有散熱性能優異、直流電阻小和結構緊湊等優勢，同時電機定子槽型為矩形，采用扁銅線可以提高電機的槽滿率，因此在本文電機設計方案中繞組為扁銅線。從圖2所示的扁線平繞詳細模型中可以看出扁銅線的排列方式，并命名這種排列方式為扁線平繞，圖2a為扁線平繞的三維詳細模型，圖2b為扁線平繞的二維截面模型。

（a）三維模型

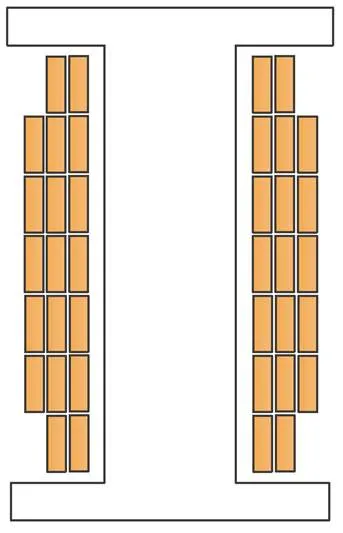
（b）二維截面

圖2 扁線平繞詳細模型

Fig.2 Detailed model of flat wire parallel winding

2 混合解析計算

2.1 采樣磁通密度

為解決三維瞬態場有限元計算交流銅耗存在計算時間較長和對計算機性能要求高的問題，本文提出一種混合解析計算的方法。該方法將三維有限元仿真與解析公式相結合，以三維渦流場有限元計算的磁通密度為基礎，再利用解析公式計算出扁銅線交流銅耗。

在三維渦流場中建立扁銅線詳細模型，并計算磁通密度。因為計算精確的磁通密度所需要的網格密度遠遠小于計算精確的交流銅耗所需要的網格密度，所以具有求解速度更快和計算資源要求更低的優勢。混合解析計算需要對磁通密度進行采樣，本文將采用分部分、分段和分層相結合的采樣方式。

因為建立三維模型可以考慮繞組端部效應，所以先將扁銅線繞組分成4個部分進行采樣，分別為內徑端部繞組部分、左側槽內繞組部分、外徑端部繞組部分和右側槽內繞組部分，如圖3a所示。每部分將分段進行采樣，分段依據是每根導體的磁通密度分布情況。當單根導體磁通密度分布不均勻時，以磁通密度明顯變化之處為分界線進行分段。以右側槽內繞組第一根導體為例，分成3段進行采樣，如圖3b所示。為了減少采樣點的數量，當單根導體磁通密度分布均勻時，導體不進行分段，作為一個整體進行采樣。由于扁銅線受到趨膚效應、鄰近效應和外部磁場的影響，磁通密度在單根導體截面上分布不均勻。為解決這個問題，每段將分成個小截面進行采樣，假設每個小截面上磁通密度分布是均勻的，并且在其有效長度上是恒定不變的，如圖3c所示。圖中，為扁銅線導體高度，為扁銅線導體寬度，eff為扁銅線導體有效長度，h為截面高度，B為截面磁通密度。

（a）采樣部分

（b）采樣分段

（c）采樣截面

圖3 磁通密度采樣

Fig.3 Magnetic flux density sampling

基于采樣坐標系確定每個采樣點的坐標，如圖4所示。采樣點磁通密度可表示為B，其中表示采樣部分，表示采樣分段，表示采樣截面。當=1時對應采樣點在右側槽內繞組，當=2時對應采樣點在外徑端部繞組，當=3時對應采樣點在左側槽內繞組，當=4時對應采樣點在內徑端部繞組。以右側槽內繞組和外徑端部繞組為例，分別推導采樣點坐標的表達式。右側槽內繞組采樣點1mn的坐標為

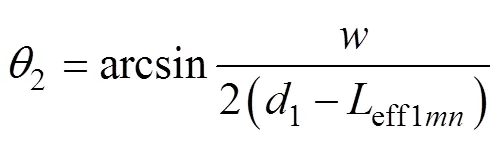
式中，1mn、1mn、1mn分別為右側槽內繞組采樣點的軸、軸和軸坐標；1m(n-1)為右側槽內繞組采樣點上一個小截面的軸坐標，其中1m0為右側槽內導體初始軸坐標；和都為從1開始逐漸遞增的正整數，最大值取決于導體磁通密度的分布情況；1為右側槽內繞組到原點的最大距離；eff1mn為右側槽內繞組采樣點所在分段的長度；1為最內側繞組的跨度角；2為最內側繞組與采樣點的跨度角；h為采樣點所在小截面的高度；h(n-1)為采樣點上一個小截面的高度，其中h0=0。

圖4 采樣坐標系

外徑端部繞組采樣點2mn的坐標為

式中，2mn、2mn、2mn分別為外徑端部繞組采樣點的軸、軸和軸坐標；2m(n-1)為外徑端部繞組采樣點上一個小截面的軸坐標，其中2m0為外徑端部導體初始軸坐標；2為外徑端部繞組的內側到原點的最大距離；eff2mn為外徑端部繞組采樣點所在分段的長度；eff2(m+1)n為外徑端部繞組采樣點下一分段的長度。

2.2 交流銅耗計算

由趨膚效應、鄰近效應和外部磁場引起的附加銅耗定義為繞組渦流損耗。交流銅耗ac由直流銅耗dc和繞組渦流損耗eddy組成，有

其中，直流銅耗為

式中，p為電機相數；為相電流；dc為直流電阻。

因為每段導體分成個小截面進行采樣，所以根據疊加原理將每個小截面的繞組渦流損耗相加就是每段導體的繞組渦流損耗[15]，有

式中，為角頻率；為銅的電導率；tn為每個截面磁通密度切向分量；ln為每個截面磁通密度軸向分量。

因為對每部分導體分段進行采樣，所以根據疊加原理將每段的繞組渦流損耗相加就是每部分導體的繞組渦流損耗，有

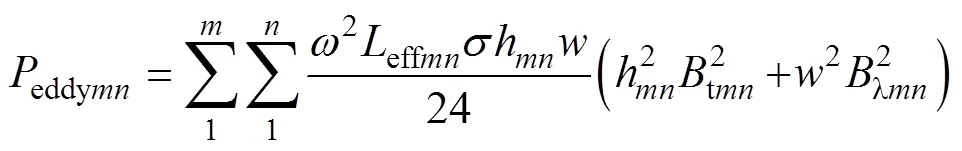
式中，effmn為每段導體有效長度；tmn為每段導體磁通密度切向分量；lmn為每段導體磁通密度軸向分量。

因為單根導體分部分進行采樣，所以根據疊加原理將每部分的繞組渦流損耗相加就是單根導體的繞組渦流損耗，有

式中，effqmn為每部分導體有效長度；h為每部分導體截面高度；tqmn為每部分導體磁通密度切向分量；lqmn為每部分導體磁通密度軸向分量。

繞組總渦流損耗就是將每根扁銅線繞組渦流損耗相加，有

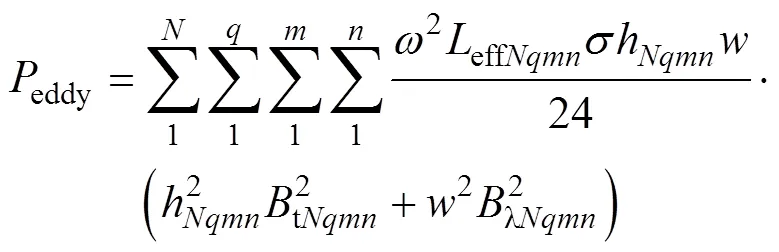
式中，為導體數量；effNqmn為每根導體有效長度；h為每根導體截面高度；tNqmn為每根導體磁通密度切向分量；lNqmn為每根導體磁通密度軸向 分量。

3 三維有限元驗證

3.1 扁線平繞三維有限元驗證

為了驗證混合解析計算的準確性，本文對一臺額定功率為60 kW的軸向磁通永磁電機進行三維有限元分析，電機主要參數見表1。

表1 電機主要參數

圖5為扁線平繞三維磁通密度分布，槽內扁銅線磁通密度分布規律為越靠近槽口，其幅值越大。端部繞組的磁通密度也符合同樣的規律，但是其幅值小于槽內繞組。圖6為扁線平繞三維電流密度分布，其槽口處導體電流密度分布更不均勻，更趨近于導體表面。

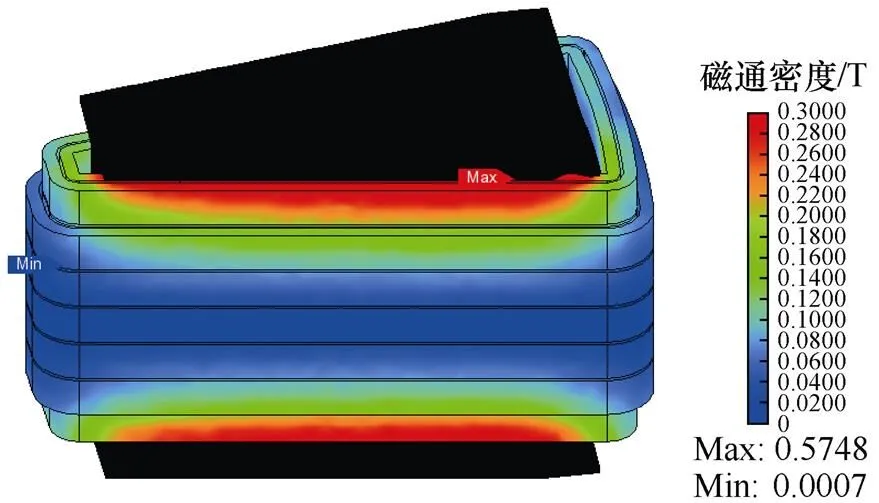
圖5 扁線平繞三維磁通密度分布

圖6 扁線平繞三維電流密度分布

當電機為額定工況時，分別利用三維瞬態場有限元和混合解析計算對每根導體的交流銅耗進行計算，如圖7所示。將三維瞬態場有限元結果和混合解析計算結果進行對比，兩者的吻合度較高。槽內導體每一列的分布規律都是沿軸向方向先減小后增大，在槽中心處達到最小值。每一行的分布規律都是沿著周向方向逐漸減小。

（a）扁線平繞導體編號

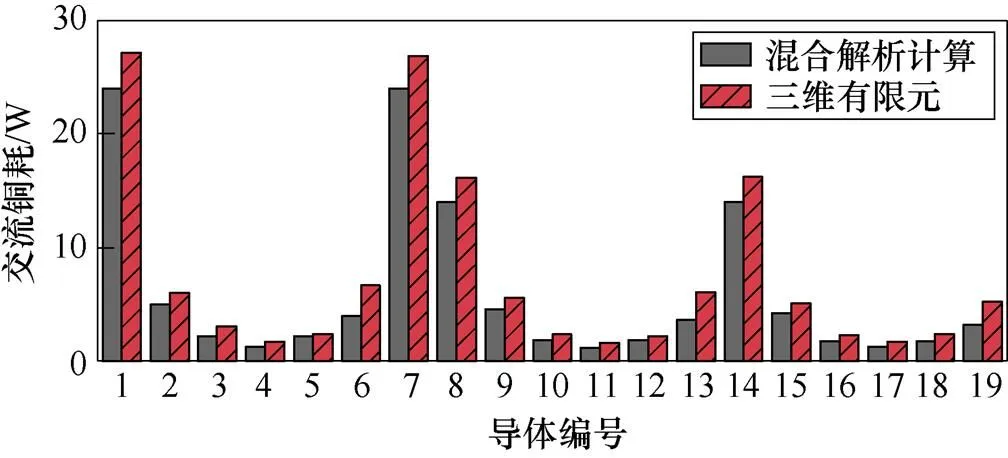
（b）導體交流銅耗對比

圖7 扁線平繞導體交流銅耗

Fig.7 Flat wire parallel winding conductor AC copper loss

通過改變電機轉速，研究不同頻率時兩種方法對計算交流銅耗的影響如圖8所示。隨著頻率升高，扁線平繞的交流銅耗增加的速率越來越大，證明頻率是影響交流銅耗的重要因素。扁線平繞交流銅耗的有限元結果與混合解析計算結果的對比見表2。隨著頻率升高，兩種方法的交流銅耗誤差逐漸增大，這是因為繞組渦流損耗占總交流銅耗的比例逐漸增大。

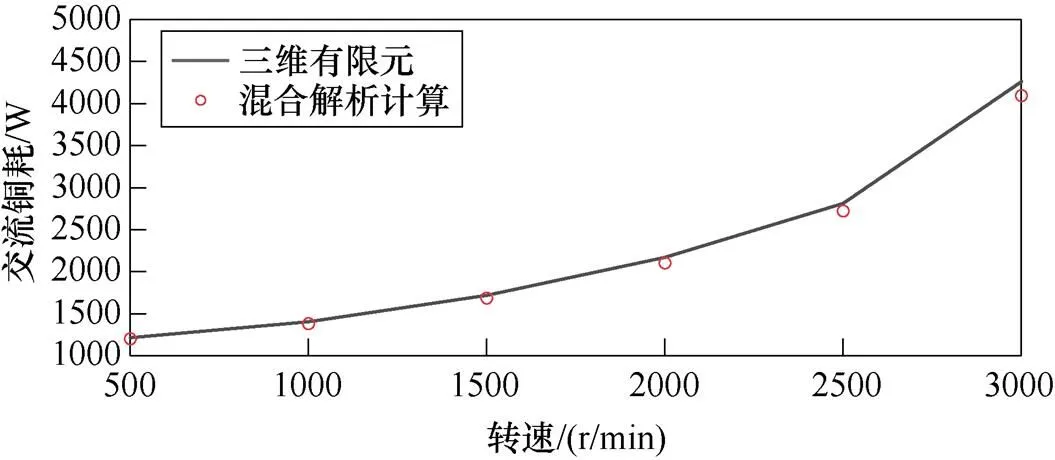
圖8 不同速度扁線平繞交流銅耗

3.2 扁線立繞三維有限元驗證

為了抑制扁線平繞的交流銅耗，將采用不同的導體排列方式，并命名為扁線立繞。圖9a為扁線立繞的三維詳細模型，圖9b為扁線立繞的二維截面模型。

表2 扁線平繞交流銅耗對比

（a）三維模型

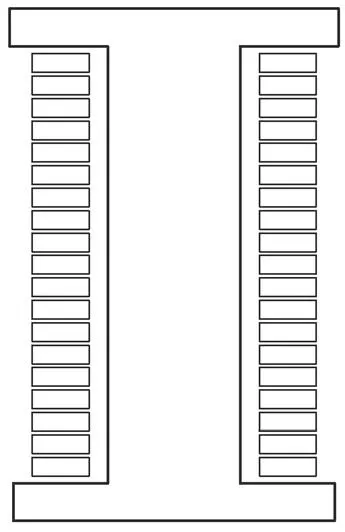
（b）二維截面

圖9 扁線立繞詳細模型

Fig.9 Detailed model of flat wire vertical winding

圖10為扁線立繞三維磁通密度分布，槽口處導體磁通密度幅值最大，與扁線平繞相比，磁通密度較大的導體數量降低。圖11為扁線立繞三維電流密度分布，槽口處導體電流密度分布更趨近于表面，電流密度分布不均勻的導體數量降低。

圖10 扁線立繞三維磁通密度分布

圖11 扁線立繞三維電流密度分布

將扁線立繞的導體進行編號，當電機為額定工況時，分別利用三維瞬態場有限元和混合解析計算對每根導體的交流銅耗進行計算，如圖12所示。扁線立繞交流銅耗的軸向分布規律與扁線平繞相同。對比圖7和圖12可知，扁線平繞中導體7、8和14更靠近槽口處，而扁線立繞中導體19更靠近槽口處，這些導體的交流銅耗會更大，這個現象符合磁通密度與電流密度的分布規律。因此，設計電機時應選擇槽口導體數量較少的排列方式。

（a）扁線立繞導體編號

（b）導體交流銅耗對比

圖12 扁線立繞導體交流銅耗

Fig.12 Flat wire vertical winding conductor AC copper loss

圖13為不同轉速時分別采用混合解析計算和三維瞬態場有限元計算的扁線立繞交流銅耗結果。扁線立繞交流銅耗的有限元結果與混合解析計算結果的對比見表3。對比表2和表3可以看出，扁線平繞的交流銅耗一直大于扁線立繞，并且隨著電機轉速增加，電機頻率迅速升高，兩者的交流銅耗差也越來越大。通過對比三維瞬態場有限元仿真結果，在額定工況下，扁銅線交流銅耗減小了36.9%。

圖13 不同轉速扁線立繞交流銅耗

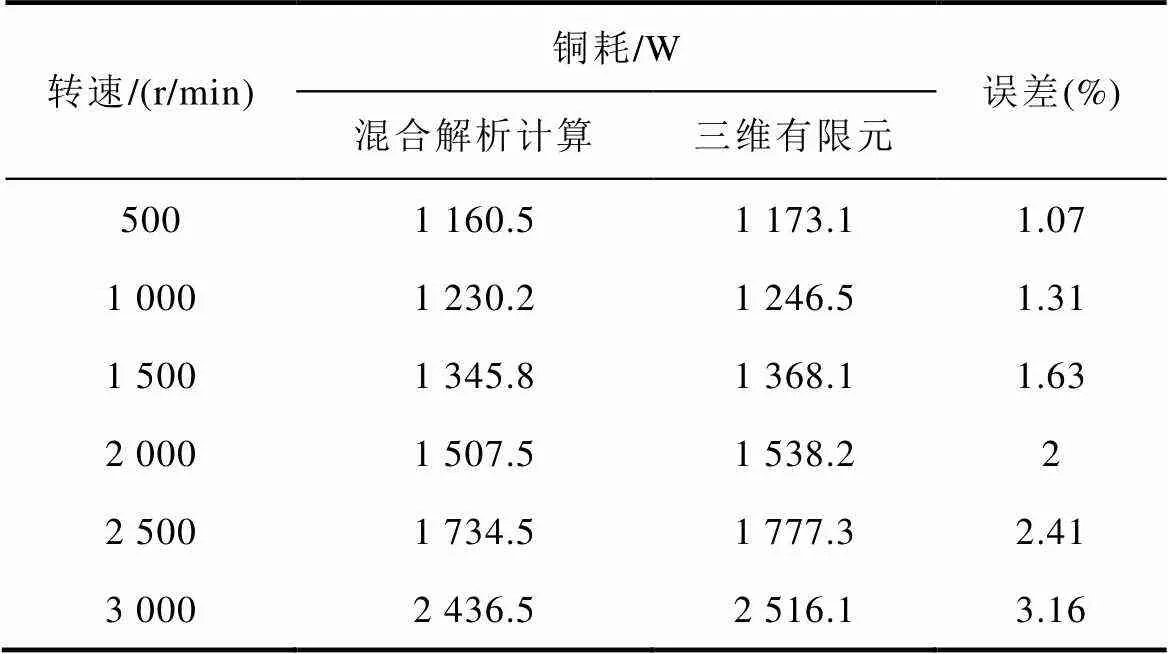
表3 扁線立繞交流銅耗對比

與三維瞬態場有限元相比，混合解析計算的最大誤差為3.93%。三維瞬態場有限元的計算時間為49 h，混合解析計算的計算時間為1 h，計算時間縮短了97.96%。因此，利用該方法計算交流銅耗具有計算精度高和計算時間短的優勢。

3.3 對比不同工況下電機性能

為了全面對比兩種導體排列方式，利用混合解析計算和三維瞬態場有限元分別計算了三種常用工況下電機的交流銅耗和效率。電機的三種工況見表4。工況Ⅰ為相對低速大轉矩工況，工況Ⅱ為額定工況，工況Ⅲ為相對高速工況。

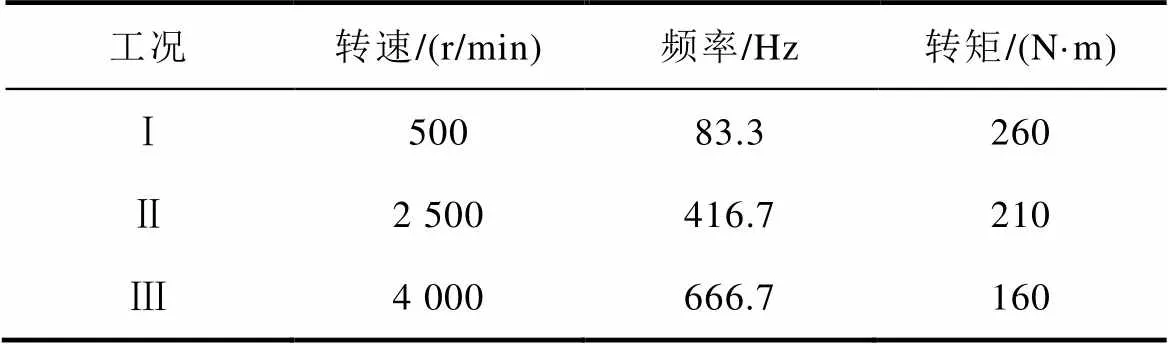
表4 電機三種工況

圖14和圖15分別為兩種導體排列方式在不同工況下的交流銅耗和效率，混合解析計算與三維瞬態場有限元的計算結果吻合度較高。在工況Ⅰ下，扁線平繞的交流銅耗略高于扁線立繞，因為轉速較低，繞組渦流損耗占總交流銅耗的比例不大。在工況Ⅱ和工況Ⅲ下，扁線立繞的效率明顯大于扁線平繞。因為頻率迅速升高，繞組渦流損耗占總交流銅耗的比例變大。綜上所述，扁線立繞電機的性能要優于扁線平繞電機，證明了扁線立繞的有效性。為充分發揮扁銅線優勢，需要通過選擇合理的導體排列方式來抑制扁銅線交流銅耗，并提高電機效率。

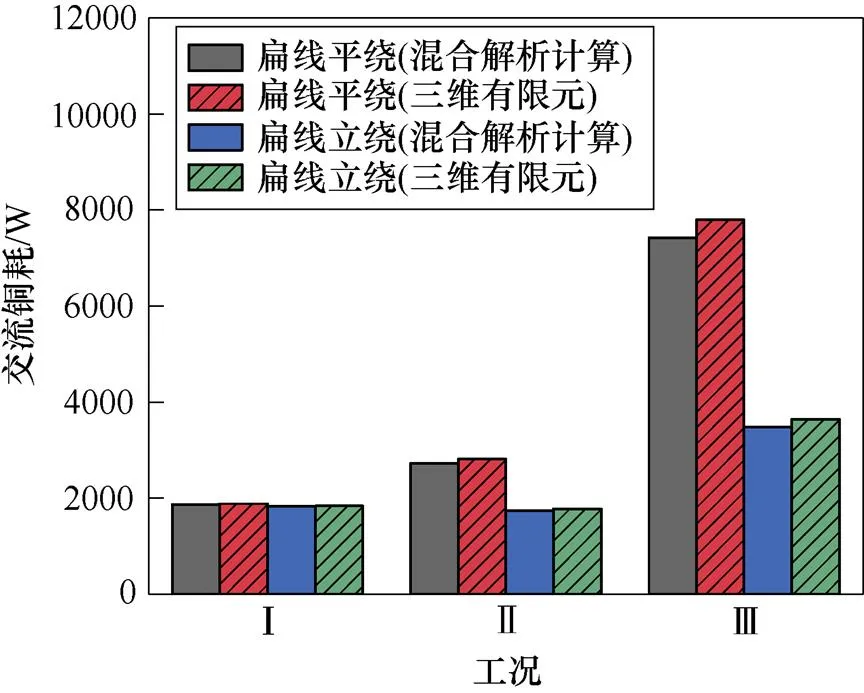
圖14 不同工況交流銅耗

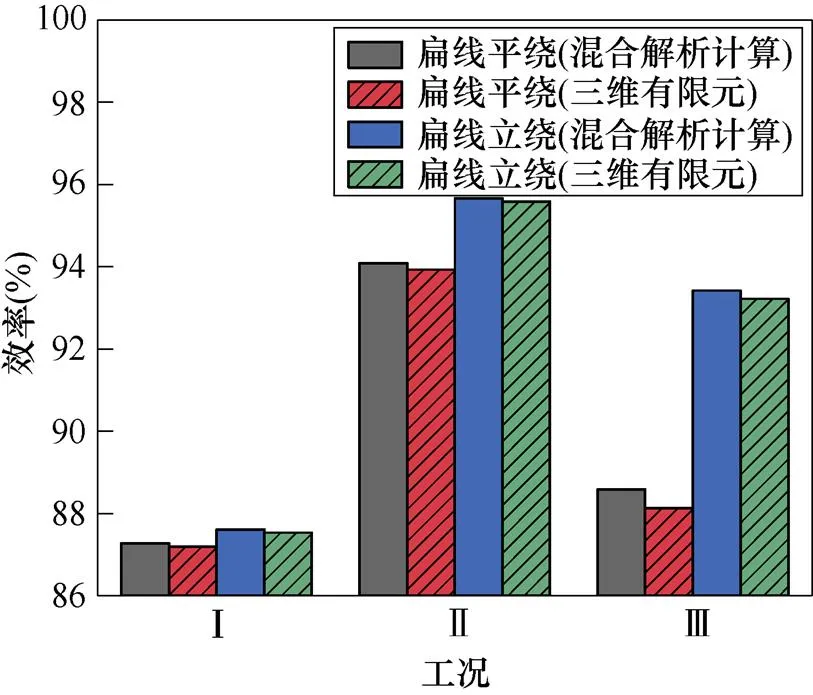
圖15 不同工況效率

4 實驗驗證

為了驗證混合解析計算的準確性，根據表1電機參數，設計并制造了一臺樣機。繞組的線型為扁銅線，并采用扁線立繞的導體排列方式。扁銅線結構與樣機如圖16所示，樣機實驗平臺如圖17所示。額定轉速2 500 r/min的線空載反電動勢波形如圖18所示，證明樣機滿足設計條件可正常運行。

圖16 繞組結構與樣機

圖17 電機測試實驗平臺

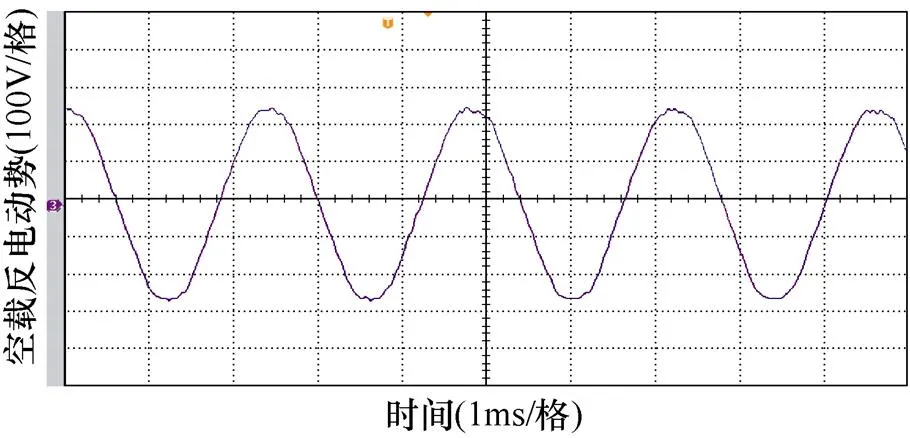
圖18 空載反電動勢波形

轉速為2 500 r/min時的相電流與效率的關系如圖19所示。混合解析計算與實驗的誤差很小，在合理的范圍之內。產生誤差的原因是當相電流較小時，機械損耗的計算值和實驗值存在誤差，機械損耗所占比例較大，因此導致混合解析計算的效率高于實驗效率。綜上所述，實驗結果、三維有限元仿真結果和混合解析計算結果均基本吻合，證明了混合解析計算的準確性與扁線立繞的有效性。

圖19 效率對比

5 結論

本文將三維有限元與解析法相結合，提出一種混合解析計算的方法來快速計算扁銅線交流銅耗。同時提出扁線立繞的導體排列方式來抑制扁銅線交流銅耗。對不同工況和不同導體排列方式的交流銅耗和效率進行了分析研究。通過對比混合解析計算結果、三維瞬態場有限元仿真結果和實驗結果，得到以下結論：

1）本文提出扁線立繞的導體排列方式，可以有效抑制扁銅線交流銅耗，提高電機效率。在額定工況下，與扁線平繞相比，扁線立繞的交流銅耗減小了36.9%。并且隨著頻率增加，差異越來越明顯。因此，為抑制交流銅耗應盡可能減小槽口處的導體數量，選擇合適的導體排列方式。為在不改變電機拓撲結構的前提下，抑制扁銅線交流銅耗提供了參考。

2）混合解析計算方法可以考慮趨膚效應、鄰近效應和外部磁場對扁銅線交流銅耗的影響。利用該方法計算交流銅耗具有計算精度高和計算時間短的優勢。該方法還適用于快速分析不同扁銅線排列方式對交流銅耗的影響，為快速準確地計算扁銅線交流銅耗提供了參考，同時也為優化高功率密度電機設計提供了基礎。

[1] Cheng Wenjie, Cao Guangdong, Deng Zhikai, et al. Analytical solution for electromagnetic torque of ultrahigh speed AFPM motor with slotless stator core and toroidal coils[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-5.

[2] 張文晶, 徐衍亮, 李樹才. 新型盤式橫向磁通永磁無刷電機的結構原理及設計優化[J]. 電工技術學報, 2021, 36(14): 2979-2988.

Zhang Wenjing, Xu Yanliang, Li Shucai. Structure principle and design optimization of a new type of disk transverse flux permanent magnet brushless motor[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2979-2988.

[3] 徐衍亮, 崔波, 張文晶, 等. 軟磁復合材料-Si鋼組合鐵心盤式橫向磁通永磁無刷電機[J]. 電工技術學報, 2020, 35(5): 983-990.

Xu Yanliang, Cui Bo, Zhang Wenjing, et al. Disk transverse flux permanent magnet brushless motor based on soft magnetic composite-Si steel core[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 983-990.

[4] 朱龍飛, 朱建國, 佟文明, 等. PWM逆變器供電引起的軸向磁通非晶電機諧波損耗的解析計算[J]. 電工技術學報, 2017, 32(16): 115-123.

Zhu Longfei, Zhu Jianguo, Tong Wenming, et al. Analytical calculation of harmonic losses of an axial flux amorphous motor caused by PWM inverter supplying[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 115-123.

[5] Payza O, Demir Y, Aydin M. Investigation of losses for a concentrated winding high-speed permanent magnet-assisted synchronous reluctance motor for washing machine application[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.

[6] 駱凱傳, 師蔚, 張舟云. 基于溫度實驗的永磁同步電機損耗分離方法[J]. 電工技術學報, 2022, 37(16): 4060-4073.

Luo Kaichuan, Shi Wei, Zhang Zhouyun. Method of loss separation of permanent magnet synchronous motor based on temperature experiment[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4060-4073.

[7] 許欣, 鄧智泉, 張忠明, 等. 高速電機定子單槽繞組交流損耗近似解析建模及驗證[J]. 中國電機工程學報, 2021, 41(12): 4306-4316.

Xu Xin, Deng Zhiquan, Zhang Zhongming, et al. Approximate analytical modeling and verification of AC loss of stator single slot winding of high-speed motor[J]. Proceedings of the CSEE, 2021, 41(12): 4306-4316.

[8] 張琪, 張俊, 黃蘇融, 等. 集膚效應對高密度永磁電機溫升的影響[J]. 電機與控制應用, 2013, 40(8): 35-39.

Zhang Qi, Zhang Jun, Huang Surong, et al. Influence of skin effect on temperature rise of high density permanent magnet motor[J]. Electric Machines & Control Application, 2013, 40(8): 35-39.

[9] Aliyu N, Ahmed N, Stannard N, et al. AC winding loss reduction in high speed axial flux permanent magnet machines using a lamination steel sheet[C]// 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 2019: 1053-1060.

[10] Geng Weiwei, Zhang Zhuoran. Analysis and imple- mentation of new ironless stator axial-flux permanent magnet machine with concentrated nonoverlapping windings[J]. IEEE Transactions on Energy Con- version, 2018, 33(3): 1274-1284.

[11] Heins G, Ionel D M, Patterson D, et al. Combined experimental and numerical method for loss separation in permanent-magnet brushless machines[J]. IEEE Transactions on Industry Applications, 2016, 52(2): 1405-1412.

[12] Fatemi A, Ionel D M, Demerdash N A O, et al. A computationally efficient method for calculation of strand eddy current losses in electric machines[C]// 2016 IEEE Energy Conversion Congress and Expo- sition (ECCE), Milwaukee, WI, USA, 2017: 1-8.

[13] Volpe G, Popescu M, Marignetti F, et al. Modelling AC winding losses in a PMSM with high frequency and torque density[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 2300-2305.

[14] Mohammed O A, Ganu S. FE-circuit coupled model of electric machines for simulation and evaluation of EMI issues in motor drives[J]. IEEE Transactions on Magnetics, 2010, 46(8): 3389-3392.

[15] Taran N, Ionel D M, Rallabandi V, et al. An overview of methods and a new three-dimensional FEA and analytical hybrid technique for calculating AC winding losses in PM machines[J]. IEEE Transactions on Industry Applications, 2021, 57(1): 352-362.

[16] 高華敏, 張卓然, 王晨, 等. 定子無鐵心軸向磁場永磁輪轂電機損耗分析及效率優化[J]. 中國電機工程學報, 2021, 41(6): 2002-2012.

Gao Huamin, Zhang Zhuoran, Wang Chen, et al. Loss analysis and efficiency optimization of stator coreless axial magnetic field permanent magnet hub motor[J]. Proceedings of the CSEE, 2021, 41(6): 2002-2012.

[17] 朱灑, 曾峰, 陸劍波, 等. 考慮PWM諧波損耗的車用扁線內嵌式永磁同步電機效率圖簡化工程計算[J]. 電工技術學報, 2022, 37(22): 5687-5703.

Zhu Sa, Zeng Feng, Lu Jianbo, et al. Simplified engineering calculation of efficiency map of interior permanent magnet synchronous machines with hairpin windings considering PWM-induced harmonic losses[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5687-5703.

[18] Zhang Jian, Zhang Zhuoran, Xia Yiwen, et al. Thermal analysis and management for doubly salient brushless DC generator with flat wire winding[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 1110-1119.

[19] Liu Kai, Yin Ming, Hua Wei, et al. Design and optimization of an external rotor ironless BLDCM used in a flywheel energy storage system[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.

[20] Luo Ciyong, Sun Jun, Liao Yong, et al. Analysis and design of ironless toroidal winding of tubular linear voice coil motor for minimum copper loss[J]. IEEE Transactions on Plasma Science, 2019, 47(5): 2369- 2375.

[21] Popescu M, Dorrell D G. Proximity losses in the windings of high speed brushless permanent magnet AC motors with single tooth windings and parallel paths[J]. IEEE Transactions on Magnetics, 2013, 49(7): 3913-3916.

[22] Ishigohka T, Ninomiya A, Yamaguchi S, et al. Effect of impedance distributions on current imbalance in insulated multi-stranded superconducting conductor[J]. IEEE Transactions on Applied Superconductivity, 2000, 10(1): 1216-1219.

[23] Bian Xu, Liang Yanping. Circuit network model of stator transposition bar in large generators and calculation of circulating current[J]. IEEE Transa- ctions on Industrial Electronics, 2015, 62(3): 1392- 1399.

[24] Zheng Liping, Wu T X, Acharya D, et al. Design of a super-high speed permanent magnet synchronous motor for cryogenic applications[C]//IEEE Inter- national Conference on Electric Machines and Drives, San Antonio, TX, USA, 2005: 874-881.

[25] Mellor P, Wrobel R, McNeill N. Investigation of proximity losses in a high speed brushless permanent magnet motor[C]//Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, 2006: 1514-1518.

Hybrid Analytical Calculation and Suppression of AC Copper Loss of Flat Copper Wire in Axial Flux Permanent Magnet Motor

（School of Electrical Engineering Shenyang University of Technology Shenyang 110870 China）

Axial flux permanent magnet motor is suitable for the field with high requirements on motor perfor- mance and installation space due to advantages such as high-power density, small volume, and light mass. In the field of high-power density motors, flat copper wire is used for its high slot-filling rate and excellent heat dissipation performance. However, due to the influence of skin effect, proximity effect, and external magnetic field, the flat copper wire has a higher AC copper loss, which can seriously affect the motor performance and the insulating material life. Therefore, accurate calculation and suppression of AC copper loss of flat copper wire are significant.

Although accurate results can be obtained using the three-dimensional transient field to calculate AC copper loss, some issues, such as long computing time and high computer performance requirements, could be improved. Therefore, a hybrid analytical calculation method is proposed to balance calculation accuracy and calculation time. This method combines the three-dimensional finite element with the analytical method, which can consider the influence of skin effect, proximity effect, and external magnetic field on AC copper loss. Meanwhile, a conductor arrangement of flat wire vertical winding is proposed to suppress AC copper loss.

Firstly, according to the actual size of the winding, a detailed three-dimensional model of flat copper wire is established in the eddy current field, and the magnetic flux density is calculated. Secondly, the combined sampling method of parts, segments, and layers is adopted. Finally, the sampling magnetic flux density is combined with the analytical model to calculate the AC copper loss.

A 60 kW, 18-slot, 20-pole double-rotor single-stator axial flux permanent magnet motor was taken as an example. Firstly, the proposed method analyzed the AC copper loss of different conductor arrangements, verified by a three-dimensional transient field finite element. The AC copper loss of the flat wire vertical winding is reduced by 36.9% compared with that of the flat wire parallel winding, and the hybrid analytical calculation time is reduced by 97.96% compared with the three-dimensional transient finite element. Secondly, the AC copper loss and motor efficiency under different working conditions were analyzed. The flat wire vertical winding motor’s performance is better than the flat wire parallel winding motor in all working conditions, and its advantages are more obvious with the increase in frequency. Finally, the prototype was tested. The experimental results, the finite element results, and the hybrid analytical calculation results were almost consistent, which verified the accuracy of the hybrid analytical calculation and the effectiveness of the flat wire vertical winding.

The following conclusions can be obtained by comparing the calculation results of the three methods: (1) The conductor arrangement of flat wire vertical winding is proposed, effectively suppressing the AC copper loss of flat copper wire and improving motor efficiency. The number of conductors at the slot opening should be reduced, and the conductor arrangements should be changed to suppress AC copper loss without changing the motor topology structure. (2) The influence of skin effect, proximity effect, and external magnetic field on AC copper loss of flat copper wire can be considered by the hybrid analytical calculation method. This method has the advantages of high accuracy and short calculation time in calculating AC copper loss, which is also suitable for rapidly analyzing the effect of different flat copper wire conductor arrangements on AC copper loss.

Axial flux permanent magnet motor, flat copper wire, AC copper loss, hybrid analytical calculation, conductor arrangement

TM351

10.19595/j.cnki.1000-6753.tces.221828

國家自然科學基金面上項目（51877139）和遼寧省教育廳科學研究經費（面上項目）（LJKZ0128）資助。

2022-09-30

2023-03-22

武 岳 男，1995年生，博士研究生，研究方向為軸向磁通永磁電機設計、控制及多物理場分析。E-mail: wuyue_95@126.com

張志鋒 男，1981年生，教授，博士生導師，研究方向為特種電機設計及其控制。E-mail: zzf_sut@126.com（通信作者）

（編輯 崔文靜）