新能源接入電網振蕩中心快速識別方法

章玉杰,劉 緒,龐家彧,單 哲,劉艷梅

(1.國網江蘇省電力有限公司超高壓分公司,江蘇 南京 211100;2.國網遼寧省電力有限公司物資分公司,遼寧 沈陽 110006)

0 引言

“雙碳”目標下,構建以風電、光伏、水電等新能源為主體電源的新型電力系統成為主流趨勢[1]。隨著新能源接入電網的比例日益提高,其間歇性、波動性、隨機性等特點對電網的安全穩定運行帶來較大的影響,尤其當發生新能源大面積脫網和外送通道發生三相短路等嚴重故障時,電網振蕩和暫態穩定性問題突出[2-4]。此外,新能源通過電力電子裝置大規模并網,導致接入近區送端電網動態行為愈趨復雜,穩定特性發生了巨大變化,保障電網安全的穩定控制技術在以電力電子型設備為主要設備的新型電力系統中面臨新的需求和挑戰。

近年來,隨著相量測量單元(PMS)在電力系統的廣泛應用,挖掘廣域量測系統(WAMS)實時、全局電力大數據中反映系統穩定特征的關鍵數據進行暫態穩定分析與控制、距離保護振蕩閉鎖以及失步解列等技術成為研究熱點[5-8]。文獻[8]通過研究系統振蕩中心聯絡斷面電壓與系統暫態失穩功角的映射關系,提出了一種基于振蕩中心聯絡斷面受擾電壓軌跡時域積分的暫態失穩判別方法。

基于理論研究成果,學術界和工業界對基于電網廣域測量大數據的安全穩定控制技術在高比例新能源接入電網中的實際應用進行了探索[9-12]。工程應用結果表明,基于廣域響應的穩定控制技術能夠快速、有效地對系統穩定性進行評估;但同時也存在一定的不足,如依賴于能夠敏感反映系統穩定特征的振蕩中心觀測點的選取,目前大多采用啟發式人工選點方式。因此,研究如何在電網受擾后快速辨識系統重要斷面振蕩中心、確定重點觀測站點,對于電網穩定控制具有重要意義。

關于電力系統振蕩中心的研究,文獻[13]較早地揭示了其變化原因并研究了系統發生失步振蕩時電壓公式及其變化特征,提出了基于Ucosφ的失步解列裝置啟動判據。文獻[14]針對基于本地量的失步解列裝置進行了研究,提出了利用阻抗角的變化時序及功率變化過零點判斷振蕩中心是否在線路上的方法。文獻[15]指出傳統失步解列裝置存在的問題,并提出了自適應解列的必要性。振蕩中心在上述暫態失穩判別和失步解列研究中具有重要地位,其運行特征和原理也有較多的研究。文獻[16]提出了一種利用線路兩側電氣量頻率的差異識別系統振蕩中心的方法。文獻[17]研究了機電暫態仿真過程中振蕩中心的計算方法、振蕩中心的特點和變化規律。文獻[18]研究了線路阻抗不均導致振蕩中心偏移的規律。

本文在前期理論研究和工程應用基礎上,進一步充分利用廣域測量大數據的全局性和實時性的特點,深入研究了電力系統發生擾動后,系統振蕩中心的變化過程與機理,提出一種基于廣域量測大數據的電力系統振蕩中心快速識別方法。該方法無需考慮系統和線路阻抗,僅需少量觀測點電壓量測相量數據即可快速篩選并確定受擾后系統重要斷面(線路)振蕩中心位置。通過IEEE39節點系統算例和中國南方電網實際電網算例驗證了本文方法的有效性,可為新能源接入電網受擾后系統振蕩薄弱斷面快速識別提供參考。

1 振蕩中心的定義

在電力系統振蕩過程中,通常可等效為兩機群振蕩模式,可近似采用如圖1所示的兩機等值系統來描述其電氣特性[13]。

圖1 等值兩機系統

圖1中,EM和EN分別為兩側等值機群電勢,C點為系統振蕩中心。兩機等值系統電壓相量圖如圖2所示。

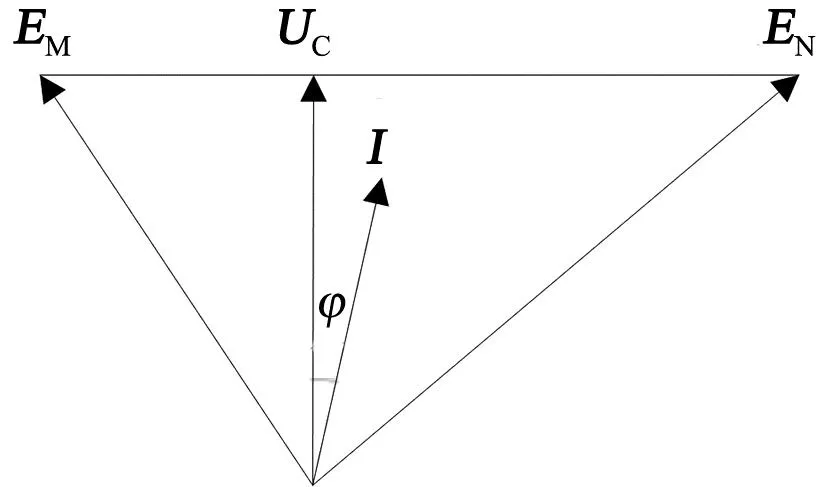
圖2 等值兩機系統電壓相量圖

兩機系統發生振蕩時,在兩側電勢角度差逐漸變大的過程中,兩系統中間各點電壓會發生變化,最低點電壓逐漸降低,這個電壓最低點就是振蕩中心。因此,振蕩中心定義為電力系統振蕩過程中同調機群之間電壓幅值最小的點,通常位于2個區域和地區之間的聯絡線上。

2 線路振蕩中心識別方法

振蕩中心是電壓幅值最小的點,如果線路存在振蕩中心,則該點的電壓低于線路兩端母線電壓。圖3中電壓最低點落在線路外側,即線路中不存在振蕩中心,圖4中電壓最低點落在線路中間,即線路中存在振蕩中心。

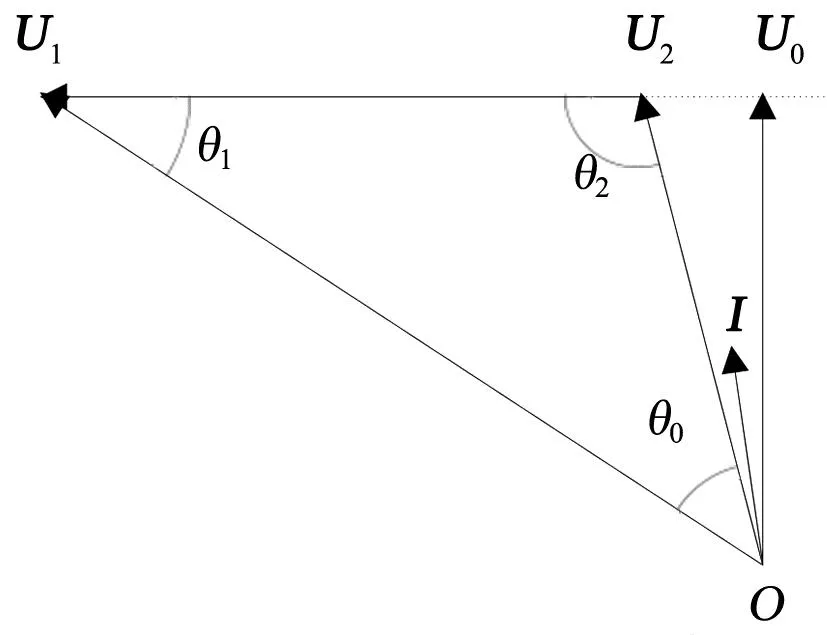
圖3 不存在最低電壓的線路電壓相量圖

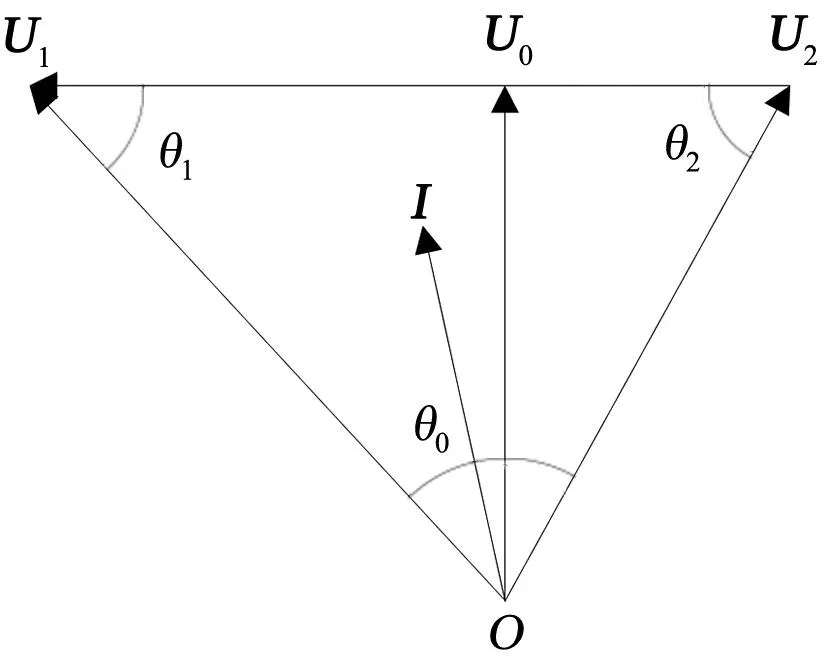
圖4 存在最低電壓的線路電壓相量圖

如圖4所示,設線路兩側電壓相量為U1和U2,相角差為θ0,U1與U1-U2相角差為θ1,U2與U2-U1相角差為θ2。假定線路上各點電壓沿著U1和U2之間的連線均勻分布,則振蕩中心電壓為與該連線垂直的電壓,即圖4中的U0。

根據余弦定理得:

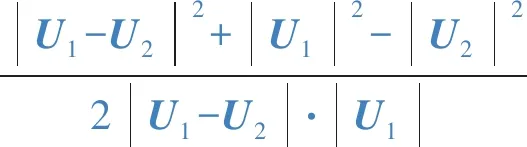
(1)

(2)

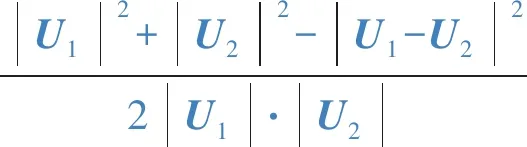
(3)

記|U1|=k|U2|,則有:

|U1-U2|2=(k2+1)|U2|2-2k|U2|2cosθ0

(4)

由相量圖可知,θ1和θ2均為銳角,于是有:

(5)

聯立式(4)和式(5),可得線路存在振蕩中心的充要條件判據為

(6)

記振蕩中心距離線路一側距離與線路長度之比為ρ,則:

(7)

振蕩中心電壓幅值為

(8)

3 基于廣域信息的振蕩中心識別

通過分析推導可知,系統振蕩中心存在于1條或幾條關鍵線路上。可通過廣域量測系統實時獲取系統線路兩側的電壓幅值和相角信息對系統振蕩中心進行實時識別和跟蹤,實現步驟如下。

a. 選擇觀測線路,對指定線路進行實時監測,并獲取其兩側母線電壓幅值和相角信息;

b. 利用式(6)判據對觀測線路進行振蕩中心識別,記錄線路振蕩次數和振蕩中心位置;

c. 根據線路振蕩中心電壓和振蕩次數篩選主振蕩線路,確定系統的振蕩中心。

具體算法實現流程如圖5所示。

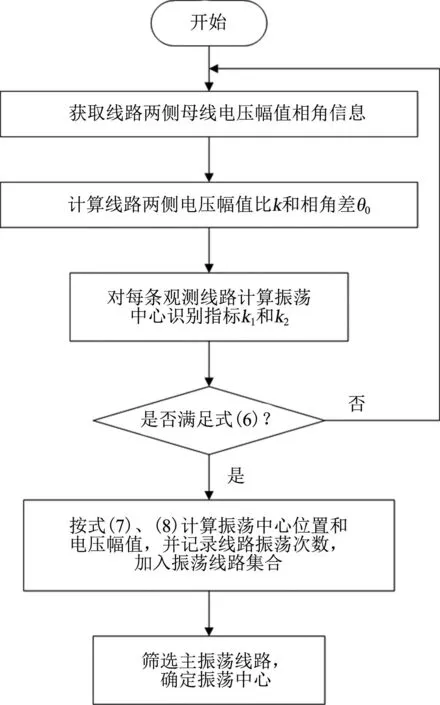
圖5 振蕩中心識別流程

4 算例分析

4.1 IEEE39節點系統算例

IEEE39節點系統結構如圖6所示,采用PSD-BPA軟件時域仿真結果模擬實時廣域量測數據,仿真步長為0.02 s,仿真時長為6 s,觀測線路34條。

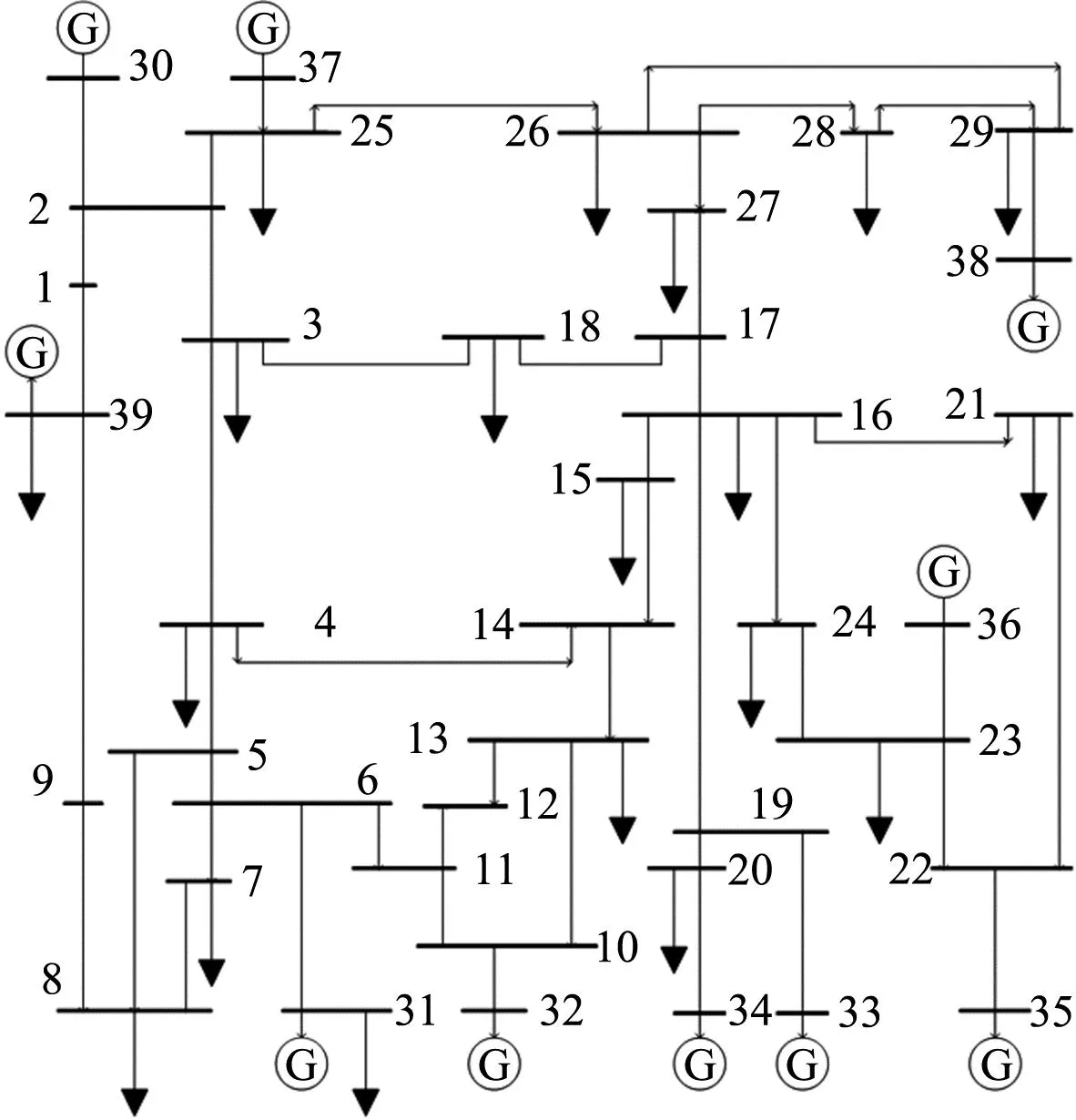
圖6 IEEE39節點系統結構

算例1:線路4-14母線4側0.18 s發生三相短路故障,0.4 s切除線路(系統穩定)。

共有24條線路存在振蕩中心,選取了其中3條振蕩線路,線路排序如表1所示。線路8-9振蕩次數最多、電壓最低。

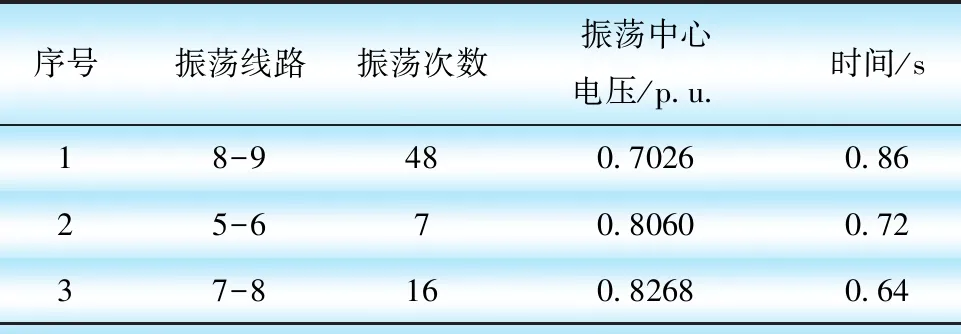
表1 線路4-14三相短路故障振蕩線路統計

線路8-9和線路5-6振蕩中心位置和電壓幅值變化曲線如圖7所示。

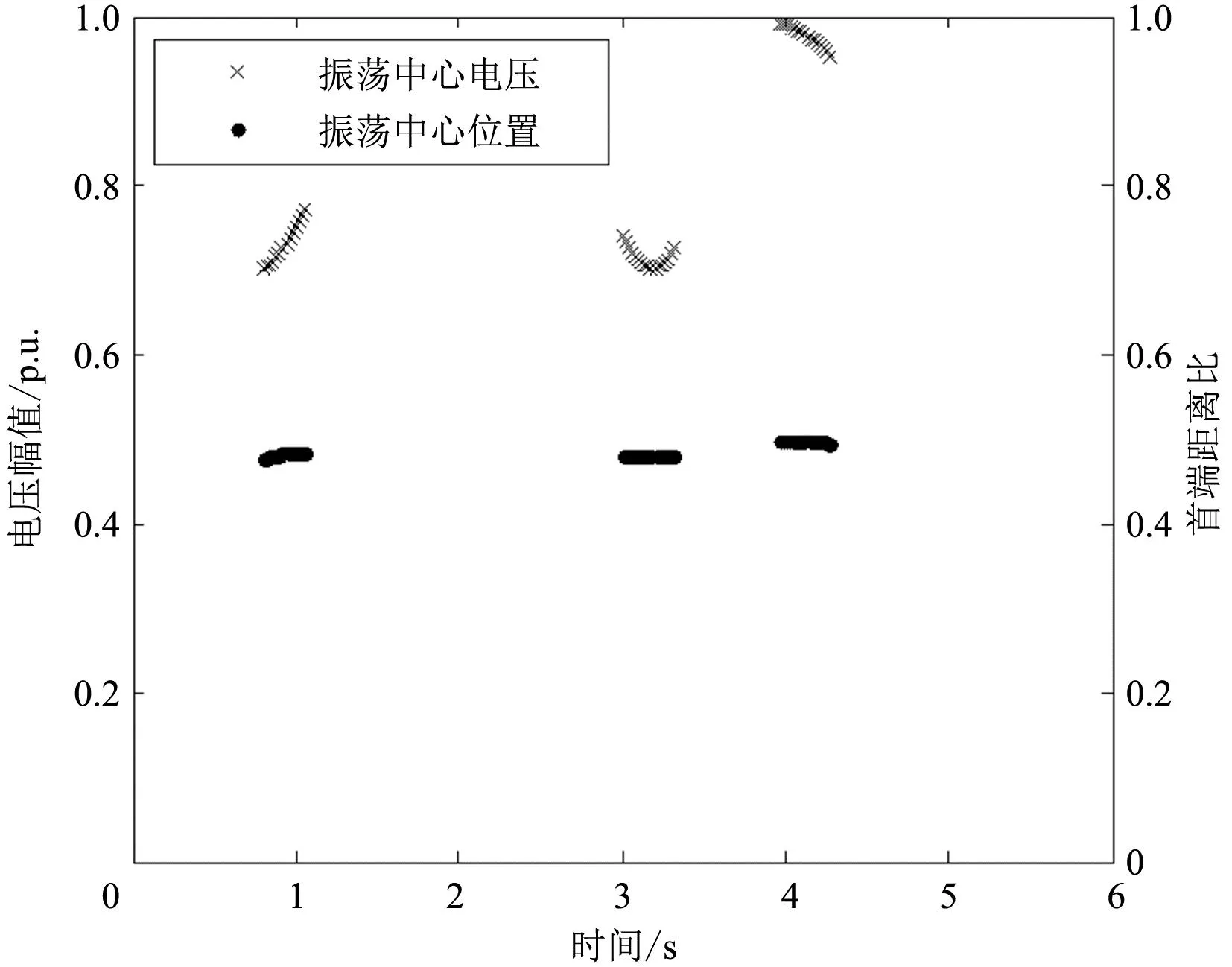
(a)線路8-9

算例2:線路3-18母線3側0.18 s發生三相短路故障,0.4 s切除線路(系統失穩)。

共有21條線路存在振蕩中心,選取了其中3條振蕩線路,線路排序如表2所示。

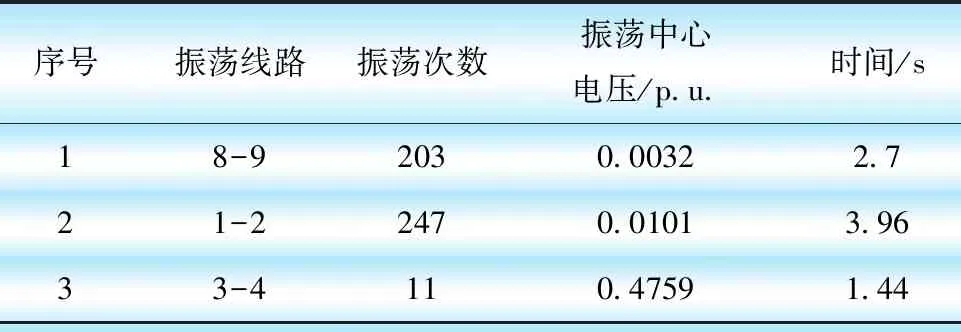
表2 線路3-18三相短路故障振蕩線路統計

線路8-9和線路1-2振蕩中心位置和電壓幅值變化曲線如圖8所示。線路1-2、8-9為重要輸電通道,線路8-9發生三相短路后,發生潮流轉移,導致線路1-2和線路8-9功率振蕩。

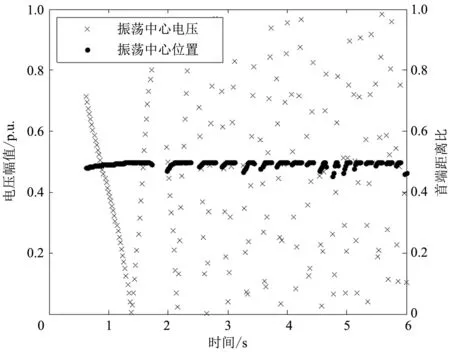
(a)線路8-9

4.2 南方電網實際系統算例

以貴州六盤水電網為研究對象,進一步驗證本文所提方法有效性。電網結構如圖9所示,總裝機約2225 MW,水電風電等新能源裝機約640 MW(占比約28.7%),負荷水平在790～1200 MW,電力外送功率較大,送端電網特征明顯。當重要輸電通道發生三相短路故障切除后,系統潮流短時間內大量轉移,易發生暫態穩定性問題。采用PSD-BPA軟件時域仿真結果模擬廣域測量數據,運行方式為某年豐大方式。仿真步長為0.02 s,仿真時長為4 s,觀測線路16條。

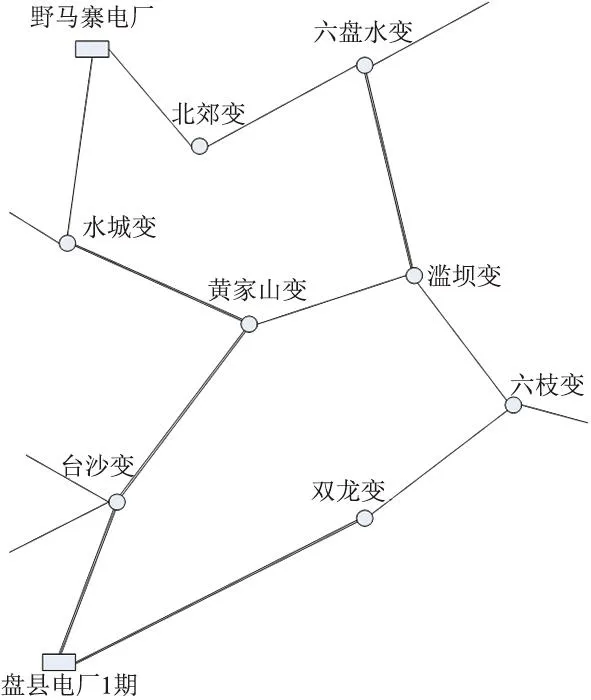
圖9 六盤水電網結構

算例1:盤縣-雙龍線(盤縣電廠側)0.18 s三相短路故障,0.3 s切除線路(穩定)。

共有11條線路出現振蕩,選取了其中3條振蕩線路,線路排序如表3所示。

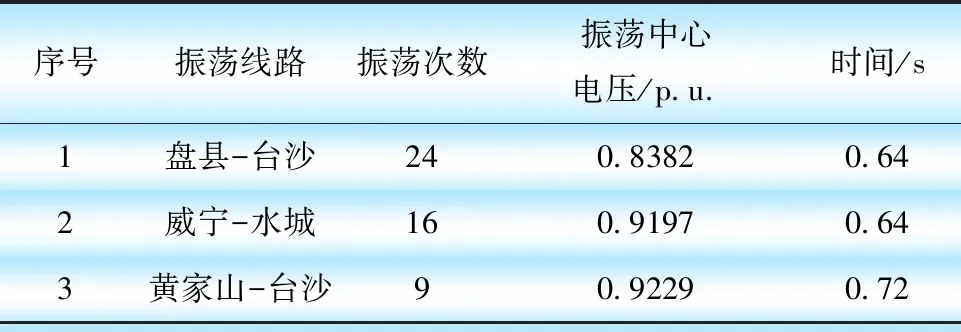
表3 盤雙線三相短路故障振蕩線路統計

線路盤縣-臺沙和威寧-水城振蕩中心位置和電壓幅值變化曲線如圖10所示。

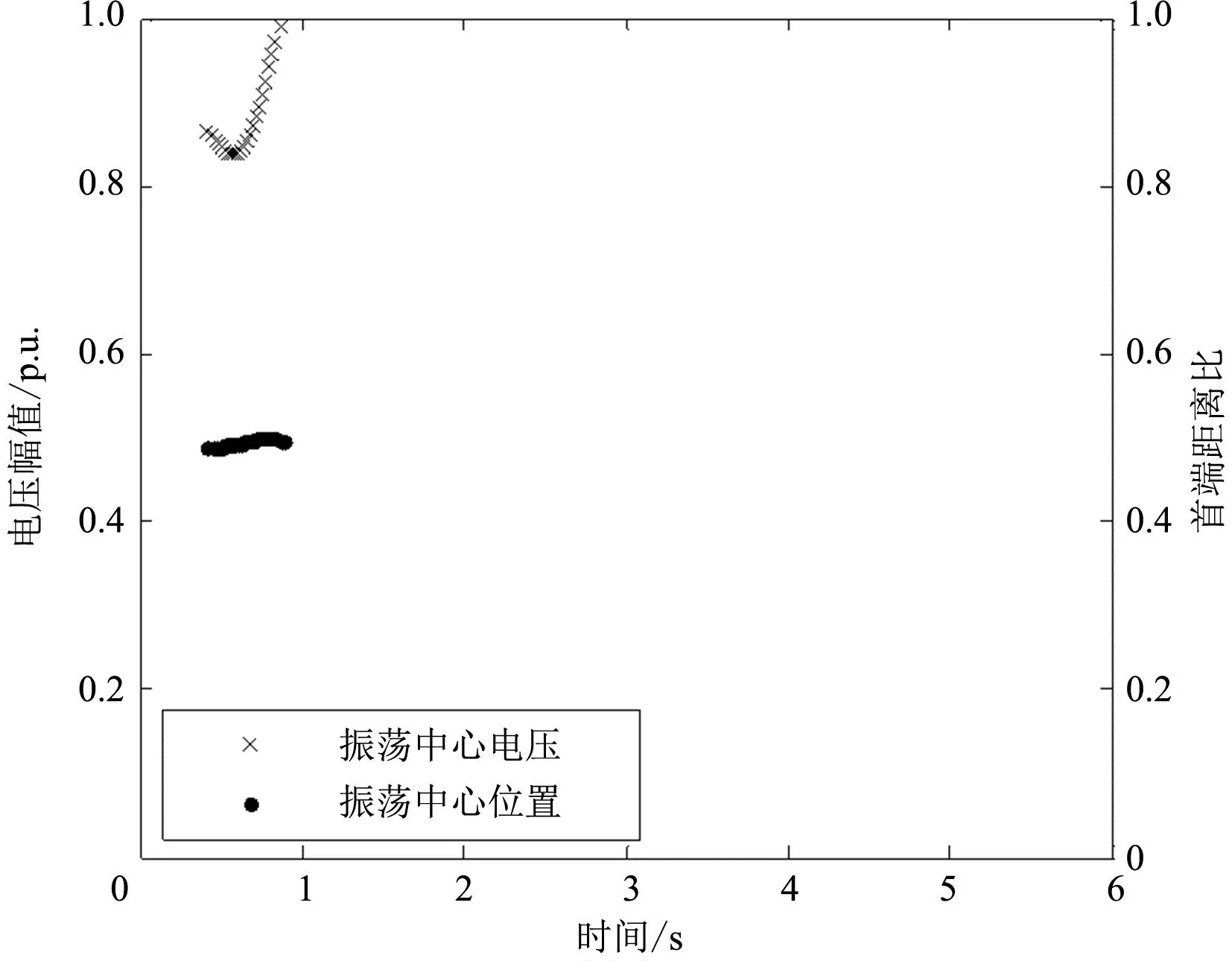
(a)盤縣-臺沙

盤臺和盤雙線作為盤縣電廠外送電力通道,當盤雙線路發生三相短路故障切除后,外送功率轉移至盤臺線,發生明顯的功率振蕩現象。

算例2:盤縣-臺沙線(盤縣電廠側)0.18 s三相短路故障,0.3 s切除線路(失穩)。

共有12條線路出現振蕩,選取了其中3條振蕩線路,線路排序如表4所示。

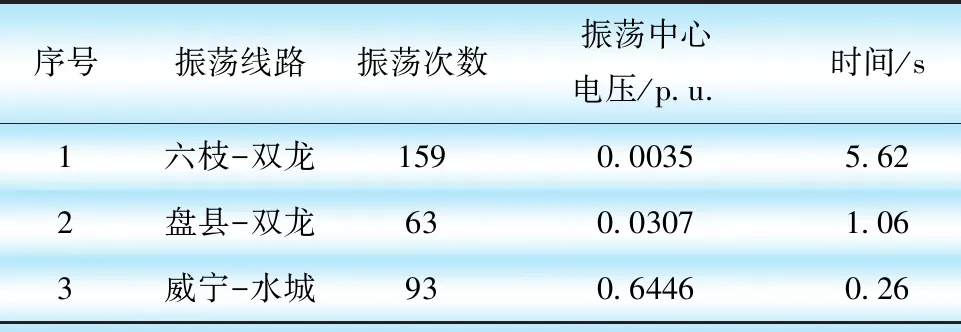
表4 盤臺線三相短路故障振蕩線路統計

線路六枝-雙龍和盤縣-雙龍振蕩中心位置和電壓幅值變化曲線如圖11所示。當盤臺線故障切除后,盤縣電廠外送功率轉移至盤雙線、六雙線,超出線路功率限額,系統暫態失穩,振蕩明顯。

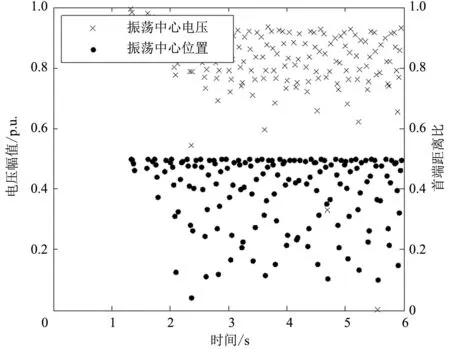
(a)六枝-雙龍

4.3 算例小結

根據算例分析,電網重要輸電通道發生三相短路故障等大擾動后,重要斷面或線路存在明顯振蕩,其振蕩中心的分布和變化規律呈現如下特點:

a. 在系統振蕩過程中,部分線路會出現明顯的振蕩特征,可選擇出現振蕩中心次數較多、電壓較低的線路作為重點觀測線路;

b. 系統穩定時,線路出現振蕩中心次數較少,振蕩中心電壓也較高;系統失穩時,線路出現振蕩中心次數較多,且振蕩中心電壓較低,接近于零;

c. 振蕩中心電壓的高低反映了系統的安全穩定狀態,振蕩中心電壓越低,系統的穩定水平越差;

d. 可根據振蕩中心聯絡斷面電氣量進行進一步暫態穩定性判定,避免對全網數據的依賴。

5 結語

本文重點研究了新能源接入電網發生嚴重故障后、暫態過程中重要斷面存在振蕩中心的識別判據、振蕩中心的特點以及振蕩中心的位置變化規律。利用廣域測量大數據全局性和實時性的特點,提出了一種基于廣域測量大數據的電力系統振蕩中心識別方法,該方法能夠為基于電力大數據的新型電力系統安全穩定分析確定系統振蕩中心。通過IEEE39節點系統和中國南方電網實際系統算例分析,驗證了本文所提方法的有效性及實用性。