載荷方向不確定條件下結構動態穩健性拓撲優化設計1)

杜鼎新 王 棟

(西北工業大學航空學院,西安 710072)

引言

傳統的結構拓撲優化設計往往是在理想狀態下進行的,即結構所受的載荷環境、材料參數以及約束條件等均被認為是確定性的.如此所獲得的結構優化設計,也僅僅是針對某個(些)確定的名義設計狀態而言是最優的[1-7].然而在實際工程結構中,不確定性因素卻是普遍存在且無法避免的,如材料的物理性能、模型幾何尺寸、邊界約束條件和外界施加的載荷等[8-13].這些結構設計參數會由于工業生產的誤差、工作環境的改變以及長時間服役引起性能的退化等因素而產生變化,導致結構的實際工作狀態不再是理想和固定的,而是可變和不確定的.即使這些參數的變化范圍很小,無疑也會對結構的承力性能產生巨大的作用,最終可能對結構的響應造成不利的影響.這就意味著,如果在結構設計時僅考慮理想的確定性情形,那么所得到的系統就缺少必要的結構備份或冗余,在實際應用中缺乏足夠抵抗材料參數或載荷等不確定性因素變化的能力,其結構功能甚至可能因為這些因素的變化而提前失效[13].因此,為了使所設計的結構具有較強的抵抗不確定性因素的能力,設計者需要在其初步設計階段就主動地考慮它們的影響,而非僅關注少數幾個離散的理想設計狀態,從而使結構具有足夠的安全冗余,容忍工作狀態的可變性,且在實際應用中能正常、穩定地發揮預期的功能和效果[11-16].

相較于結構的材料屬性、邊界約束條件等因素,外載荷狀態對結構拓撲構型設計的影響更大.實際工程中,由于外部環境的變化,作用于結構上外載荷的大小、方向與位置等都可能具有一定范圍內的隨機可變性[11,16-19].因此研究載荷不確定性對結構拓撲優化設計的影響具有非常現實的工程意義.另外,大多數工程結構,如航空航天器、船舶、橋梁等,其結構在服役期內會受到各種時變載荷的作用,而一個復雜的時變周期激勵通常能近似分解為幾個簡諧激勵的疊加.因此簡諧激勵是一種非常基礎且典型的動載荷[6],研究簡諧激勵作用下結構的拓撲優化設計具有十分重要的理論和實際意義[17-18].

研究外載荷不確定性條件下結構拓撲優化設計可采用基于可靠性的拓撲優化方法(reliability-based topology optimization,RBTO)[20-24],或基于穩健性的拓撲優化方法(robust topology optimization,RTO)[9,11,16-19,24-30].兩者均可使用概率或者非概率模型表示不確定變量的變化情況.不同之處在于前者旨在滿足可靠性約束條件,而后者聚焦于減少結構性能對不確定性變量的敏感性.在穩健性拓撲優化的體系下,已經有許多關于外載荷作用方向的不確定性的研究報告[11,16-17,25-28,30].通常,結構的動柔順度響應和外激勵作用方向的變化之間并沒有一個顯性的關系式[16,28],因此難以直接分析出外激勵方向擾動對結構動柔順度的影響.本文旨在構建一種簡單且高效的計算方法,可直觀、快速地獲得結構動柔順度的概率特征指標.并基于這些特征指標,開展了考慮外載荷作用方向不確定性的穩健性結構動態拓撲優化設計.

在實際工程中,外載荷作用狀態的小幅變化往往近似地符合正態的概率分布,即圍繞著預先設定的名義狀態有著一定概率性的變化規律,因此可使用正態隨機分布對外載荷作用狀態的可變性進行描述[11,25-26].而且相應的結構動柔順度也不再是一個確定的值,但兩者之間也并非簡單的線性關系.為了高效地計算在外載荷作用方向變化情形下結構的動柔順度響應,本文首先將外載荷沿坐標軸進行投影,然后對結構的動柔順度響應進行二階泰勒展開,以便獲得動柔順度的近似表達式.并近一步推導出結構動柔順度的期望和方差的計算表達式,以及它們對拓撲變量靈敏度的顯性計算公式.按照確定性的優化策略,可完成結構在動載荷作用下的穩健性拓撲設計.保證在外激勵作用方向出現擾動時,結構的動柔順度響應不發生較大的改變.用結構動柔順度的變異系數(coefficient of variation,COV)[13]作為一種量化的穩健度衡量指標,對比分析了不同設計策略結構拓撲優化設計的穩健程度.

本文采用概率模型描述外載荷作用方向的不確定性,基于材料屬性的有理近似方法 (rational approximation of material properties,RAMP)建立了連續體結構動態拓撲優化模型.以結構動柔順度的期望值及標準差(standard deviation,STD)的加權和最小化為設計目標函數[11,16,25-27],以整體材料用量為約束條件,采用基于靈敏度分析的移動漸近方法(method of moving asymptotes,MMA)[31],研究簡諧激勵在作用方向不確定性條件下結構受迫振動穩態響應的拓撲優化問題.最后用兩個典型算例來證明本文所提方法的有效性,并與傳統的優化結果進行對比,以便驗證穩健性拓撲優化設計結果的可靠性.

1 結構穩健性拓撲優化模型

1.1 線性振動系統穩態響應分析

當外激勵頻率遠離結構的固有頻率時,可以暫時忽略結構內的阻尼.采用有限元法對連續體結構進行離散化處理,則無阻尼結構受迫振動微分方程可表示為[17]

式中,K和M分別是振動系統N×N階的剛度和質量矩陣,N表示結構的自由度數;u(t)和分別是結構的位移和加速度響應N維列陣;f(t)是系統所受外激勵列陣.假設結構受到簡諧外力的作用

其中,ω是外激勵頻率((°)/s),是一個給定的值;F(θ)是沿坐標軸方向上的外激勵幅值N維列陣

其中,奇(偶)數項表示在有限元結點處,外激勵沿x(y)軸的幅值分量;θ表示外激勵的作用方向,是一個隨機變量.假設其變化符合正態分布,即見圖1 所示.其中μθ代表外載荷作用的期望或名義方向,σθ是其標準差,代表著外載荷方向變化的概率統計偏差.嚴格地說,一個服從正態分布的隨機變量是無界的.然而按照工程實踐中廣泛使用的“3σ”法則,即對于特定的符合正態分布的隨機變量而言,它取值落在區間[μ-3σ,μ+3σ]之外的概率小于千分之三,因此便可以認為區間[μ-3σ,μ+3σ]為該隨機變量實際可能的取值區間.依據該法則,σθ的值可以通過區間寬度基本確定.由于載荷作用方向θ具有可變性,因此外激勵幅值列陣F(θ)也具有一定的不確定性.

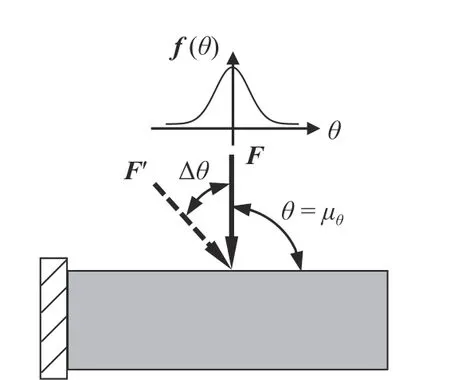
圖1 結構受具有方向不確定外載荷作用的示意圖Fig.1 Schematic of a load with the direction uncertainty imposed to a structure

對方程式(1)兩邊同時進行Fourier 變換,則可得振動系統響應的特征平衡方程

式中,D(ω)=K-ω2M是振動系統的動剛度矩陣.U(ω)是結構位移響應幅值列陣,在不考慮結構阻尼的前提下是實數,且與結構的動態性能以及激振頻率密切相關.本文采用直接方法精確計算結構在簡諧激勵作用下的穩態響應,不必考慮模態截尾帶來的計算誤差和虛假模態的干擾.求解方程(4)可得結構響應的幅值列陣U(ω),進而由Fourier 逆變換可得時域內結構的穩態動響應u(t).

1.2 結構拓撲優化數學模型

實際工程中,由于結構所處環境的變化,外載荷作用方向具有一定的可變性.因此結構的響應也具有一定的不確定性.本文以結構有限元模型中單元的相對密度ρe作為設計變量,在給定的區域內構造結構的最優拓撲構型(材料布局).考慮到動柔順度的不確定性,將設計目標函數設置為最小化結構動柔順度均值和標準差的加權和[11,16,25-27],則結構動態穩健性拓撲優化問題數學列式可表示為

式中,Cd(θ)是結構的動柔順度,它不僅與外激勵的大小有關,還與激勵作用方向θ密切相關,即隨著θ的變化而改變.因此,Cd(θ) 也是一個隨機變量.J為優化設計的目標函數,是結構動柔順度的期望,是結構動柔順度的標準差,β是權重因子,其作用是調節結構動柔順度標準差在目標函數中的占比.ρ是n維拓撲變量列陣,n代表結構的單元總數.ρmin是為了避免結構剛度矩陣奇異而設置的一個下限值(ρmin=0.001).ve是單元的體積,fv是給定的材料體分比,即材料用量的上限.

以上模型與傳統的確定性拓撲優化模型最大區別在于:結構的動柔順度Cd不再是一個確切的量,而是隨機變量θ的函數.且優化的目標函數不再僅僅針對名義設計狀態,而是綜合考量在θ的隨機變化區間內的整體設計狀態,旨在讓最終的優化設計結果具有能容忍外激勵方向變化的冗余性.這使得優化設計過程更加復雜,但也更加真實地反映了工程結構的實際受載情況.

為了合理地描述結構的動力學性能,根據以往的研究結果,本文采用RAMP 模型對單元質量和剛度矩陣進行插值,以避免虛假局部模態的產生[17]

式中,q是插值模型的懲罰因子(q=5);m0和k0分別是實體材料單元的質量和剛度矩陣.

1.3 結構動柔順度一階導數靈敏度的計算

當外激勵作用方向θ按照正態分布隨機擾動時,根據文獻[16,28]的定義,只需在外激勵的名義(理想)作用方向,即

時,對振動系統進行分析,計算結構的動態響應.并在單元層面上計算結構的動柔順度Cd0

于是,其對單元的相對密度ρe的一階導數靈敏度可由下式計算得到

其中,ue是單元的動響應幅值列陣;de=ke-ω2me是單元的動剛度矩陣.由RAMP 模型的材料插值函數式(8)可得

于是,通過有限元分析計算,即可獲得振動結構的名義動柔順度Cd0及其對拓撲設計變量的一階導數靈敏度值.但當外激勵的作用方向θ發生擾動時,如果依然通過傳統有限元方法進行分析和計算,就需要再次求解特征平衡方程式(4).這樣的計算途徑工作效率很低,尤其考慮到外激勵的作用方向可以連續地隨機變化.因此需要一種能高效獲取在外激勵方向發生變化時結構動柔順度的計算途徑.

2 外激勵方向不確定性的影響規律

2.1 載荷方向擾動對結構動柔順度的影響

假設外激勵的大小和位置保持不變,當載荷作用方向發生改變時,其傳遞路徑亦將發生改變.即外激勵作用方向的變化必然引起結構動柔順度的變化.利用二階泰勒級數展開公式,得到動柔順度Cd(θ)變化的顯性表達式,可避免振動系統動響應方程的重復求解.

在載荷位置固定的前提下,以載荷名義作用方向為中心的一個較小的區域內,可得載荷方向發生改變后,結構動柔順度Cd的近似表達式[16,28]

按照式(3)對外激勵幅值F(θ)的表達形式,首先推導其對θ的一階和二階導數

將結構的名義動柔順度改寫成

則動柔順度對載荷作用方向的一階導數可表示為

據此,可進一步計算結構的動柔順度Cd0對載荷作用方向的二階導數

根據以上推導結果,將式(10)、式(18) 和式(19)代入式(13),即可利用該表達式快速計算由于外激勵作用方向的擾動而引起結構的動柔順度值.

2.2 目標函數及其靈敏度的計算

雖然前文已經假設外激勵作用方向的變化符合隨機正態分布,但結構的動柔順度響應變化一般不符合正態隨機分布.按照優化設計目標的要求,需要高效地計算結構動柔順度響應的均值和方差.對式(13)兩邊同時分別求期望和方差可得[16]

根據θ的正態隨機分布規律,式(21)中的各協方差項均等于0[32].因此,結構動柔順度響應的均值和標準差表達式如下

于是,結構動柔順度響應的變異系數為

巖樣采用薄壁金剛石鉆頭沿垂直于巖層方向鉆取巖芯，經過鋸、磨加工成直徑為50 mm，高為100 mm，試樣兩端面不平行度不大于0.05 mm，滿足《規程》要求，60組共計180個試樣，制備部分試樣，如圖2所示，其中頂板巖石用A編號，底板巖石用B編號。試驗在RMT-150B型電液伺服巖石力學試驗系統進行單軸壓縮試驗，如圖3所示。軸向荷載采用1 000 kN力傳感器測量，軸向壓縮變形采用5.0 mm位移傳感器測量，變形精度為1.0×10-3 mm，采用位移控制方式，加載速率為0.002 mm/s，每組巖性重復進行3次試驗。煤層頂底板巖石單軸壓縮試驗結果見表1。

顯然,式(22)和式(23)建立了結構動柔順度響應Cd(θ)的概率特征值顯式表達式.無需再通過其他額外的途徑,如Monte Carlo 模擬(Monte Carlo simulation,MCS)法等[11,25,30],即可獲得結構動柔順度響應的一、二階矩以及優化設計的目標函數

這使得穩健性結構動態優化設計效率大為提高.

將式(25)對拓撲設計變量求導,可得

其中,式(26)右邊第一項由式(11)得到,其余各項可由式(11)分別對外載荷作用方向θ連續微分得到

式中,單元位移列陣對θ的一階、二階導數可利用式(16)計算得到.另外,式(27)和式(28)同樣也可以分別利用式(18)和式(19)在單元層面上對ρe求一階導數獲得.根據以上推導結果,即可利用式(26)直接計算目標函數對所有設計變量的一階靈敏度.在此基礎上,使用基于靈敏度的MMA 算法對設計變量進行迭代更新,實現結構拓撲構型的演化.此外,還要引入靈敏度過濾技術,對動柔順度靈敏度進行處理,以便消除優化過程中的棋盤格現象,確保優化結果的可行性和可靠性[16-19].

3 算例分析

下面我們用兩個算例來驗證本文所提穩健性拓撲優化算法的可行性,并與確定性拓撲優化(deterministic topology optimization,DTO)設計結果進行對比分析,觀測結構穩健性構型設計的變化情況,同時探尋結構是如何通過增加額外構件而有效提高其抵抗外載荷方向擾動能力的,進而證明所得結果的合理性.假設材料的彈性模量E=200 GPa,密度ρ=7800 kg/m3,泊松比ν=0.3.有限元分析采用四結點平面應力單元,薄板厚度為10 mm.優化過程中取過濾半徑為單元尺寸的1.5 倍,收斂條件設置為相鄰兩次迭代各設計變量的最大改變量小于0.01[31].材料體積約束系數fv=0.35,初始設計時,將所給的材料均勻分布在整個設計區域內.

3.1 簡支平板結構

簡支平板結構設計區域尺寸及邊界約束如圖2所示.理論上,結構在底邊中點承受一個集中簡諧激振力f(t)=10ejωtkN 的作用,頻率為150 Hz (ω=2π×150 (°)/s).但是由于加載環境的復雜性,外激振實際作用方向將圍繞著作用點產生一定的擾動.將設計區域均勻劃分成120×40 的有限元網格.初始設計,結構的第一階固有頻率為265.63 Hz.假設外激勵作用方向θ的標準差為 σθ=π/12.目標函數中的權重因子β=2.

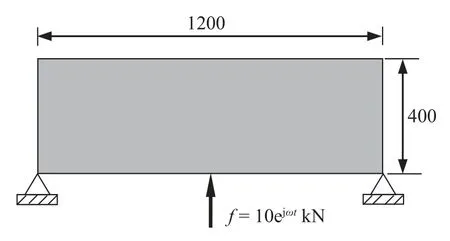
圖2 簡支平面矩形板結構Fig.2 A simply supported rectangular panel

在開展結構拓撲優化設計前,先對本文所提有關結構動柔順度均值和方差估計公式的準確性進行驗證.分別利用MCS (樣本數=105)以及式(22)和式(23)進行計算,數值結果如表1 所示.可以看出,兩種方法的結果非常接近,尤其是均值的計算結果,這足以驗證了式(22)和式(23)的有效性和準確性.此外,用本文提出的方法計算結構動柔順度均值和方差可以大幅降低計算機運算所需的時間,顯著提高優化設計的效率.

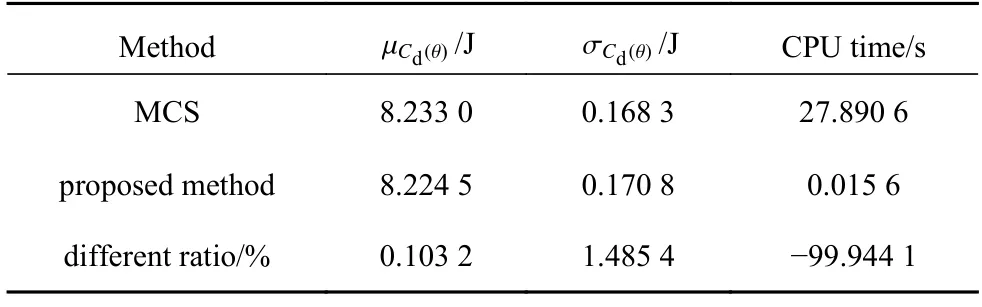
表1 兩種方法所得結構動柔順度概率特征指標對比Table 1 Comparison of the obtained stochastic measurements of the structural dynamic compliance

首先開展結構的確定性拓撲優化設計,其最優構型如圖3(a)所示.可見,垂直方向的外載荷先通過中間的兩根斜桿(或構件)傳遞到上緣,然后再通過外側的構件傳遞到支撐點(基礎).由于載荷作用方向是固定的,沒有水平方向的分力,因此結構設計區域的下緣沒有水平桿件將載荷作用點與支撐點直接連接在一起.

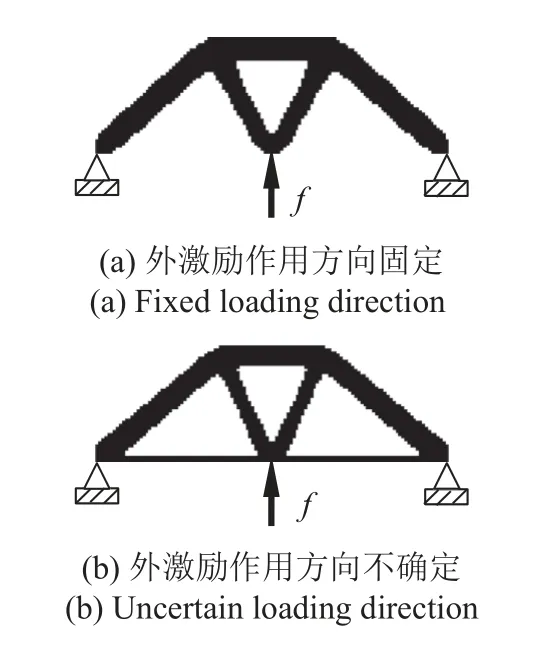
圖3 確定性和穩健性設計策略結構拓撲構型對比Fig.3 Comparison of the topology optimizations on two different design strategies of DTO and RTO

隨后,開展結構穩健性拓撲優化設計,所得最優構型設計如圖3(b)所示.兩種優化策略得到的結構構型看似基本相同,但是穩健性優化設計在結構的下緣增加了一根水平構件,從而形成了額外的兩條傳力路徑.當載荷作用方向發生擾動,不再是僅沿垂向激勵時,外激勵的水平分量將通過下緣桿件直接傳遞到支撐點.由此可知,增加的水平桿件可有效抵抗外激勵方向的擾動,能顯著提高結構在載荷作用方向不確定性情形下響應的穩健性.

表2 比較了兩種設計策略所得結構拓撲優化數值結果.雖然在確定性拓撲優化時沒有考慮外激勵作用方法的可變性,但仍可用第2 節中的方法計算其隨激勵方向隨機擾動時結構動柔順度的概率特征值.從表2 中的數值對比可知,按照穩健性拓撲優化策略所得結構動柔順度的期望、標準差以及變異系數,比確定性拓撲優化相應結果均有明顯降低,尤其是標準差以及變異系數下降幅度均超過了95%.眾所周知,這兩個特征指標能衡量不確定性數值的集中程度[32],其值越低,表明因外激勵方向變化所引起的結構動柔順度響應的變化幅度越小.即結構對外激勵作用方向擾動不再敏感,結構的穩健度更高,材料布局設計更加合理、可靠.

表2 兩種設計策略結構拓撲優化結果對比Table 2 Comparison of the numerical results with the two optimization strategies

圖4 示出了結構的動柔順度隨外激勵作用方向的變化情況.值得注意的是,當外載荷作用方向受到擾動以后,確定性設計結構的動柔順度將快速增加,即結構的動剛度明顯降低.這表明了該結構抵抗外激勵方向擾動的能力較差.相比之下,穩健性優化設計結構的動柔順度在激勵方向擾動狀態下能基本保持一致,且變化趨勢隨角度的增大而逐漸減小,這表明了穩健性拓撲優化設計能避免結構的動柔順度(剛度)發生劇烈變化,有效保持結構動態性能的穩定性.

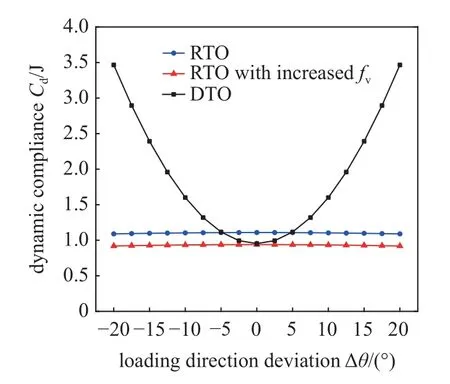
圖4 結構動柔順度隨外激勵作用方向變化情況Fig.4 Variation of the structural dynamic compliance caused by the external loading direction disturbances

然而,由圖4 還可以發現,穩健性拓撲優化設計的名義最小動柔順度Cd0比確定性相應值稍大一些(15.30%),見表2 所示.進一步比較圖3 可知,穩健性拓撲優化設計中間兩根斜撐桿的截面積,較確定性的優化設計要細一些,從而導致其名義最小動柔順度有所增大.這是因為為了提高結構抵抗外激勵方向的擾動能力,有一部分材料用來構建額外的水平承力構件,以便增加結構對外載荷傳遞的可靠性.因此在相同材料體分比條件下,穩健性拓撲優化設計結構的名義動剛度會有一定的損失.但是這部分損失可以通過適當地增加結構材料得到有效補償[4].

實際上,對于確定性拓撲優化而言,其優化設計目標僅僅是名義加載狀態下結構的動柔順度最小化,而忽略其變化情況,因此該優化策略對應的名義動柔順度值一般會更小.而穩健性拓撲優化要同時考慮在激勵方向隨機變化情形下,結構的動柔順度值及其變化和分散情況.因此穩健性設計所得動柔順度變化曲線比確定性設計對應的曲線變化更加平緩,在載荷擾動狀態下的結構動柔順度數值更加穩定.由于受材料體積的制約,穩健性設計的名義動柔順度值難免會有所上升,而優化設計過程就是要在相互妥協中找到矛盾雙方最佳的解決方案[9].

在本例中,只要將結構材料體分比增大到fv=0.358(2.29%),就可以將穩健性拓撲優化設計的名義最小動柔順度降到與確定性優化設計相同的結果,并且結構的動柔順度變化情況基本保持不變,見圖4 所示.即在少許增大結構材料用量的基礎上,結構的動柔順度響應將全面優(小)于確定性優化設計的結果.這再次表明采用本文提出的穩健性拓撲優化設計后,結構抵抗外載荷作用方向擾動的能力有了顯著地增強.

比較結構的前3 階固有頻率可以發現,結構的低階固有頻率,經過拓撲優化后都得到了明顯提高,如表3 所示.在當前激勵情形下,結構的總體動剛度較初始設計有了顯著增大,從而使結構的動響應幅值急劇減小.此外,在相同材料體分比約束條件下,穩健性拓撲優化設計的結構固有頻率要略小于確定性優化的結果,這也是為了能夠有效提高結構響應的穩健性,傳力路徑模式更新的結果.

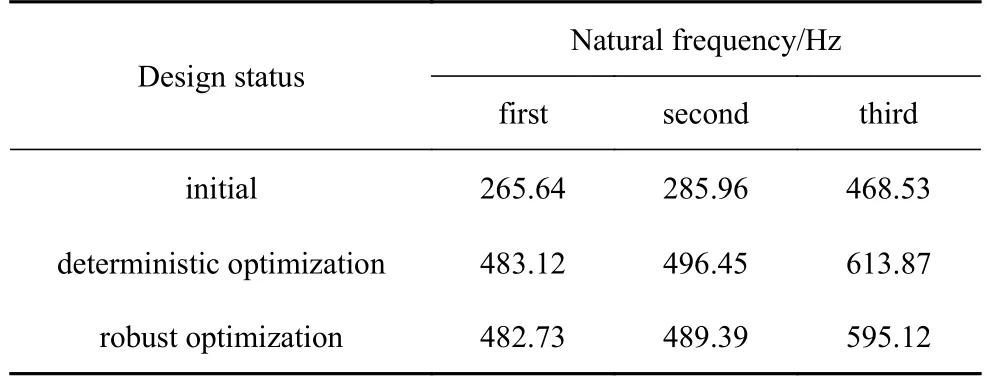
表3 簡支平板結構前3 階固有頻率比較Table 3 Comparison of the first three natural frequencies of the rectangular panel structure

此外,還有一點值得注意的是,隨著優化過程的持續運行,結構的固有頻率也會不斷提升,這就使得優化后結構的第一階固有頻率和外激勵的頻率有了較大差距,從而使得動力學優化設計問題越來越接近于靜力學優化設計問題.為了驗證該方法在高頻外激勵作用下的可行性,針對同一設計域,在外激振頻率為300 Hz,材料體積約束系數fv=0.55 (初始設計時,結構的第一階固有頻率為262.72 Hz)的條件下,再次對結構開展拓撲優化設計,結果分別如圖5 所示.可以看到,在高頻外激勵作用下,兩種不同優化策略所得結構之間的差異與低頻外激勵作用下的結果類似,穩健性優化設計仍然形成了額外兩條傳力路徑,可將外激勵的水平分量通過下緣桿件直接傳遞至支撐點.除此之外,穩健性設計的拱形傳力路徑中出現了空隙,這也是材料重新分布,額外傳力路徑消耗材料的結果.

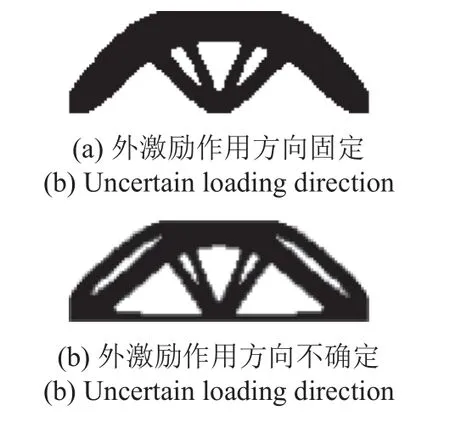
圖5 兩種設計策略結構拓撲優化在高頻外激勵條件下結果對比Fig.5 Comparison of the topology optimizations on two different design strategies under an external load of a higher frequency

表4 列出了在高頻外激勵作用下兩種拓撲優化設計所得數值結果.可以看出,穩健性優化設計仍以略微增大結構名義動柔順度的代價,大幅降低了結構動柔順度的期望、標準差以及變異系數,使得結構對高頻外激勵方向的變化不再敏感.

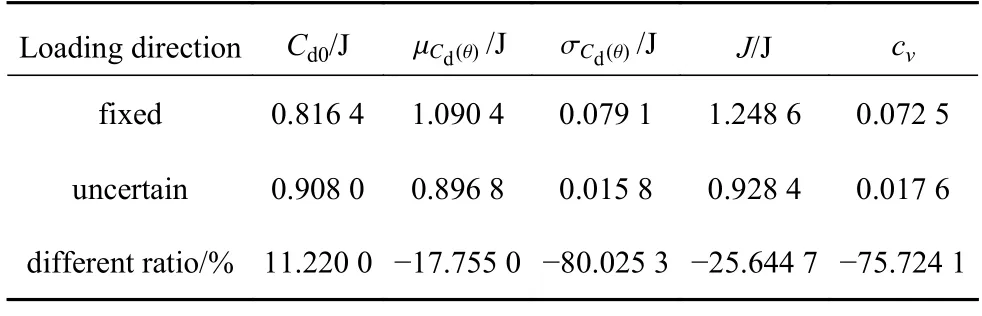
表4 兩種設計策略結構拓撲在高頻外激勵條件下優化結果對比Table 4 Comparison of the optimized results under an external load of a higher frequency

3.2 MBB 梁結構

圖6 所示為MBB 梁結構設計區域及尺寸,左、右兩端固定.理想狀況下,一個集中簡諧力f(t)=10ejωtkN 施加在梁上邊緣的中點處,外激振頻率是200 Hz.但實際上外激振實際作用方向會繞著理想方向產生一定的擾動.將結構設計區域均勻劃分成150×25 的有限元網格.假設外激勵作用方向θ的標準差為 σθ=π/54.

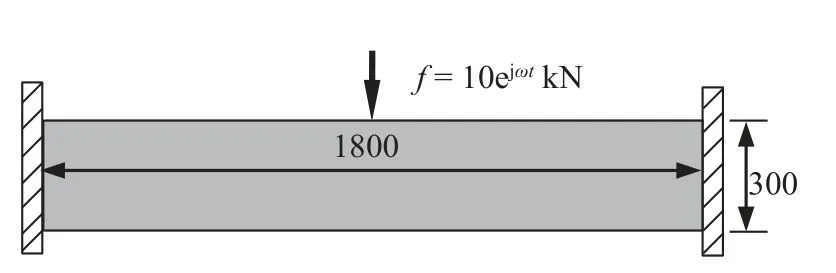
圖6 MBB 梁設計區域及外激勵Fig.6 Design domain of the MBB beam and the external force

圖7 分別示出了結構確定性和穩健性拓撲優化得到的構型設計.可以看到,兩種設計策略得到的結構拓撲優化結果仍存在著較大的差異.確定性拓撲優化設計中間兩根斜桿張成90°的夾角.表明外激勵先沿著相互正交的兩個方向傳遞到下弦,然后再傳遞到固定基礎上[9].而穩健性優化設計在外激勵作用點兩側又構建了額外的兩根斜桿,產生兩條輔助的傳力路徑.且內側兩根斜桿和下弦桿的截面尺寸均有明顯減小,以滿足對材料體積的約束.由于外激勵的作用方向具有不確定性,施加在結構上的外激勵會存在一定的水平分量,而增加的外側斜桿件能有效地將這一部分載荷傳遞至約束邊界,以抵抗外激勵方向的擾動,提高結構性能的穩健性.

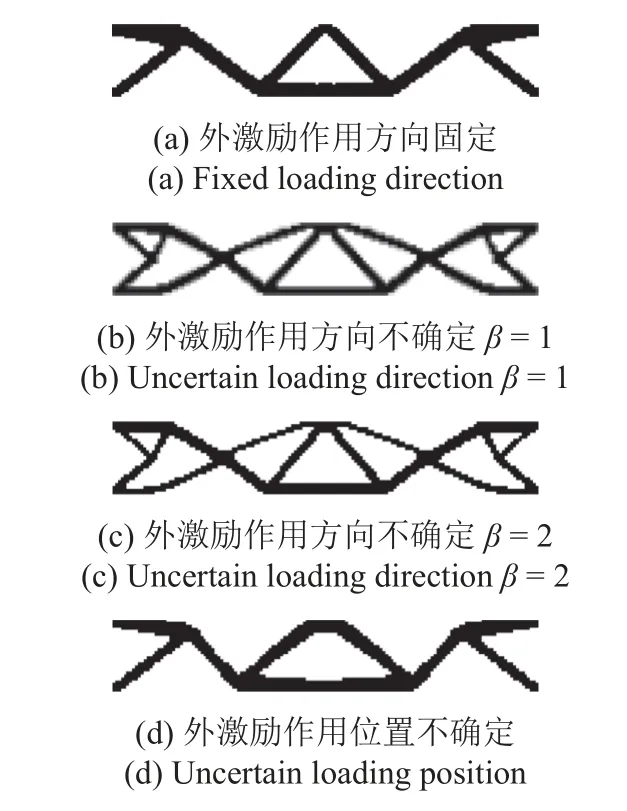
圖7 兩種設計策略結構拓撲優化結果對比Fig.7 Comparison of the topology optimizations on two different design strategies

對比圖7(b)和圖7(c)可以看出,當增大目標函數中標準差的權重因子β以后,所得穩健性優化設計中外側傾斜構件的截面積有所減小,底部路徑截面積有所增大.這使得在外激勵作用方向擾動情形下,結構動柔順度的響應值更加集中,即標準差更小.此外,文獻[9]開展了考慮外激勵作用位置不確定性的結構動態穩健性拓撲優化設計,采用區間變量表示外激勵位置的擾動,并成功獲得了該算例的穩健性最優構型設計,如圖7(d)所示.可以看到,穩健性設計只在激勵點周圍構建了作用平臺,明顯擴寬了激勵作用區域.但是,由于外載荷仍然沿豎直方向作用在結構上,因此缺少額外的傾斜傳力構件.

表5 列出了兩種設計策略結構拓撲優化數值結果.經過比較可知,考慮了外激勵方向不確定性的穩健性拓撲優化的動柔順度標準差和變異系數,均明顯小于確定性優化結果,使得結構抵抗外載荷作用方向擾動的能力更強.當權重因子β增大時,更加強調動柔順度標準差在目標函數中的占比,優化設計所得結構的動柔順度標準差會進一步降低,使得結構動柔順度的變異系數進一步減小,即結構性能的穩健度更高.

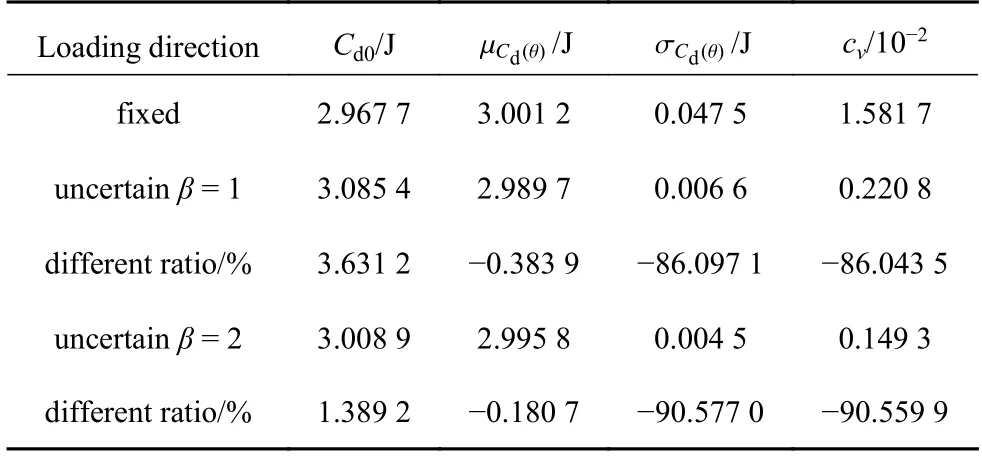
表5 結構拓撲優化結果對比Table 5 Comparison of the optimized results

如圖8 所示,當外載荷不再沿著理想方向作用時,確定性結構設計的動柔順度將快速增大.相比之下,穩健性結構設計的動柔順度變化幅度相對較小,而且隨著擾動角度的增大在逐漸減小.這說明穩健性設計的結構在外激勵名義作用方向時動柔順度最大,隨著外激勵作用方向的變化,相應的動柔順度不會超過名義激勵作用方向時的值.與前例類似,由于挪用了一定的結構材料構建額外的傳力路徑,穩健性設計結果的名義動柔順度Cd0比確定性優化相應結果稍大一些.而對比兩條穩健性設計的曲線還可以發現,當權重因子β增大以后,相應的名義動柔順度值會有所減小,而外激勵擾動狀態下的動柔順度將有所增加,總體上曲線更加平緩,即動柔順度值的離散程度以及標準差值更小,這與表4 中的數值結果相一致.總體而言,結構的動柔順度對激勵方向變化更加不敏感.

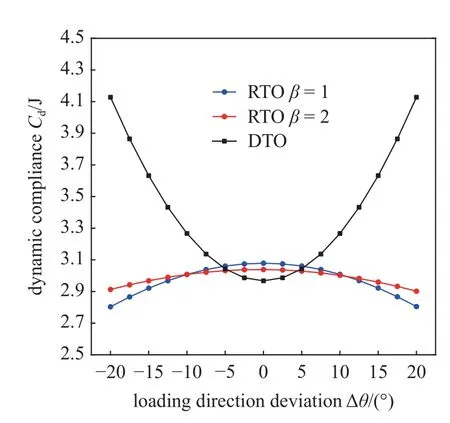
圖8 結構動柔順度隨外激勵作用方向變化情況Fig.8 Variation of the structural dynamic compliance caused by the external loading direction disturbances

圖9 分別繪出了兩種不同優化策略的名義結構動柔順度迭代收斂曲線,同時還示出了迭代的中間構型和最終優化設計結果.在穩健性設計中,額外的傾斜構件從開始即存在,為外激勵作用方向的變化提供可靠的傳力路徑.

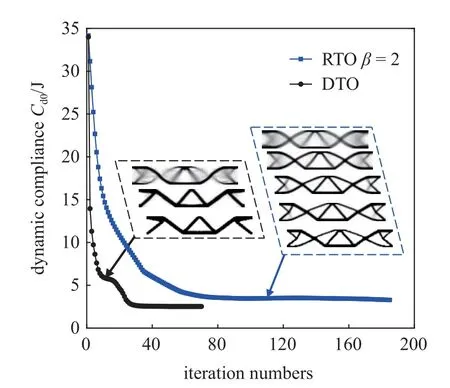
圖9 兩種設計策略拓撲優化收斂過程Fig.9 Convergence curves of the dynamic compliance on the two design strategies

4 結論

本文研究了在外激勵作用方向不確定條件下,連續體結構動態穩健性拓撲優化設計問題.假設外激勵作用方向的不確定性變化遵循正態隨機分布,借助于二階泰勒展開公式,推導了結構的動柔順度期望和標準差及其對拓撲變量的一階靈敏度顯式表達公式.以結構動柔順度均值和標準差的加權和為目標函數,充分考慮了載荷方向的不確定性對結構動響應的影響,且利用動柔順度的變異系數作為結構穩健量的衡量指標.本文用兩個典型算例,驗證了所提結構穩健性拓撲優化設計方法的可行性.分析了結構構型優化設計變化的規律,并比較了結構的動柔順度對外激勵方向擾動的抵抗能力.研究結果如下.

(1) 考慮載荷作用方向不確定性條件下得到的穩健性結構拓撲構型設計,明顯異與確定性條件下的拓撲優化結果.并且具有抵抗外激勵作用方向可變性的必要構件,在載荷方向隨機擾動情況下因而具有更可靠的傳力路徑.

(2) 當外載荷作用方向發生擾動時,穩健性拓撲優化設計的結構動柔順度變化幅度和變異系數遠低于相應的確定性優化結果.充分表明了穩健性優化設計所得結構抵抗外激勵方向擾動的能力更強,動響應變化更小,結構的性能更加穩健.

(3) 在相同體積約束情況下,穩健性拓撲優化設計的名義動柔順度稍大于相應的確定性拓撲優化結果.這是因為需要用一部分的材料構建抵抗外載荷作用方向擾動的必要構件,形成額外的傳力路徑.因而結構穩健性拓撲優化設計會損失一部分名義動剛度,以換取其抵抗載荷方向擾動能力的提高.但這部分損失的結構名義動剛度,可以通過增加少許結構材料而得到有效彌補.