波導吸振器的低頻減振設計和應用1)

趙曉宇 吳衛國 林永水 ,2)

* (武漢理工大學理學院工程結構與力學系,武漢 430070)

? (武漢理工大學綠色智能江海直達船舶與郵輪游艇研究中心,武漢 430063)

引言

板殼結構是汽車、飛機和船舶等運輸工具最常用結構形式之一,其振動與結構的安全性、疲勞壽命和環境舒適性等直接相關,板殼結構的減振研究具有重要價值.常見的被動減振技術有敷設阻尼層[1-3]、質量-阻尼振子[4-5]等,其中阻尼層存在低頻減振不明顯、附加質量大的問題,而阻尼振子則減振帶隙較窄.聲學黑洞(acoustic black hole,ABH)是近年受到廣泛關注的減振結構之一,具有寬頻減振的特性,其厚度表達式為

式中,x為ABH 尖端長度方向坐標,ε 為ABH 的厚度系數,m為大于2 的指數.因無法制造尖端厚度為零的ABH,尖端在x0處截斷,hg(x0) 為截斷厚度.

因尖端截斷厚度不為0,ABH 尖端反射系數顯著增大,Krylov[6]提出在其尖端附近黏貼阻尼材料吸收彎曲波,如圖1(a)所示.之后的學者對此構型的一維ABH 的力學特性[7-11]和設計優化[12-16]進行了探索.該ABH 的彎曲波吸收效率受黏貼阻尼材料的吸收段長度影響,但冪函數導致尖端厚度隨長度的增加急劇減小,延伸長度與尖端厚度之間的矛盾導致以往研究中的ABH 有效減振頻率高達數千赫茲,低頻彎曲波吸收效果欠佳.Morvan 等[17]和Guillaume 等[18]設計的ABH 具有更低的截止頻率,在400 Hz 以上頻率反射系數小于0.3,但其尖端厚度僅為89 μm,過薄的尖端對材料強度和加工工藝提出了更高的要求.為解決ABH 尖端過薄的問題,Tang 等[19]提出了一種經過修正的冪律ABH厚度函數,如圖1(b)所示,在冪函數的基礎上疊加了一個具有恒定截斷厚度的延伸平臺,結果表明該ABH 在低頻范圍內的彎曲波吸收效果有所提高.

圖1 3 種ABH 示意圖,淺色部分為鋼,深色部分為阻尼材料Fig.1 Three types of ABH schematics,with light colored parts made of steel and dark colored parts made of damping material

在A B H 的應用方面,多數研究基于二維ABH 進行[20-22].二維ABH 通常直接基于板殼結構本身進行加工,一旦成型便難以調整,相對而言,一維ABH 具有易安裝、可依據現實需求靈活調整的優點.Kim 等[23]和何璞[24]均將一維ABH 設計成為可安裝的振子.Zhou 等[25]設計了一種ABH 諧振梁阻尼器(ABH-RBD),該設計結合了動態減振器和波導減振器的原理,是一個連接到主體結構上的附加裝置,由于ABH 效應的魯棒性,該裝置具有不需要繁瑣的參數調整的優點.

以上研究表明,將一維ABH 設計成為可簡易安裝的振子結構是合理的選擇.但增強ABH 的延伸尖端導致其在安裝上存在一定的困難.Lee 等[26]提出了一種沿阿基米德螺旋線纏繞的螺旋ABH,對于在有限空間中安裝較長的ABH 尖端提供了可行的方案,阿基米德螺旋線半徑為

式中,r0為初始半徑,?r為半徑變化率,θ 為螺旋角度.Park 等[27]進一步研究了螺旋ABH 的螺旋線曲率對于反射系數的影響,結果表明螺旋線曲率對于ABH 的截止頻率影響很小,但該研究中ABH 的截止頻率較高.之后,Park 等[28]又提出一種基于螺旋ABH 的鋁制波導吸振器(waveguide absorber,WGA),如圖1(c)所示,并以平板均遷移率最小化為目標,優化其在簡支均勻板上的安裝位置和方向,結果表明WGA 可以在500 Hz 以內有效降低共振峰,但該研究未對WGA 的設計方法進行系統地探討.

WGA 作為一種具有易加工安裝、寬頻減振性能優良等優點的聲學黑洞新構型,其設計方法、耗能機理和減振應用效果有待進一步研究.研究基于幾何聲學和歐拉-伯努利復合梁理論,構建了WGA材料參數和幾何參數選取的理論模型,給出了材料參數和幾何參數的選取方法和原則.數值仿真分析了截止頻率的影響因素,探究了WGA 的能量耗散機理.最后開展實驗驗證了WGA 在加筋板減振應用中的效果,以期為WGA 的設計及其在工程結構減振中的應用提供指導.

1 WGA 設計方法

1.1 增強ABH 構型理論基礎

增強ABH[19]的厚度表達式為

式中,ht為附加厚度,如圖2 所示.

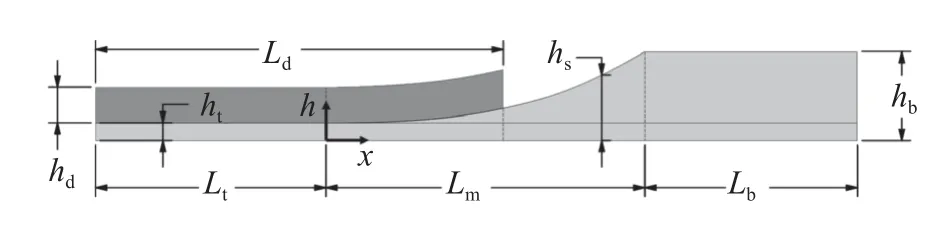
圖2 增強ABH 幾何參數Fig.2 Enhanced ABH geometric parameter

彎曲波的無反射條件[29]為

梁中彎曲波的波數為

式中,ρs為ABH 尖端基材的密度,ω 為角頻率,Es為ABH 尖端基材的彈性模量,hs=hs(x) 為ABH 尖端基材厚度.將式(5)代入式(4)可得

當 0 ≤x≤Lm且ht>0 時

將式(7)和式(8)代入式(6)可得

式(9)表明,具有附加均勻厚度的增強ABH 比經典ABH 更易滿足彎曲波無反射條件.

1.2 材料參數設計

Krylov 從幾何聲學角度給出了ABH 的反射系數計算理論[6]

式中 Imk為彎曲波的波數虛部.該式表明,要獲得更低的反射系數,需增大積分長度 [x0,x1] 和被積量Imk的大小.其中積分長度為黏貼有阻尼材料的ABH 尖端延伸長度,可通過幾何參數進行調控;波數虛部則可通過阻尼材料的損耗因子、彈性模量和厚度進行調控.

對于黏貼有阻尼層的復合梁,其彎曲波波數為

式中,ρc為復合梁的線密度,Bc為復合梁的抗彎剛度,b為復合梁寬度,ρs為基材密度,ρd為阻尼材料密度,hd為阻尼材料厚度.為在較大范圍內考慮阻尼材料彈性模量與損耗因子對 Imkc的影響,基于歐拉-伯努利梁理論,推導出帶有阻尼損耗因子的復合梁的抗彎剛度

式中,α=Ed/Es是阻尼材料和基材的彈性模量比,ηs和ηd分別是基材和阻尼材料的阻尼損耗因子,H=hd/hs為阻尼材料與基材的厚度比.

式中

其中,atan2為四象限的反正切函數,β=ρd/ρs為阻尼材料和基材的密度比.以上研究構建了材料參數選取的理論模型,依據其可探討阻尼損耗因子和彈性模量比等材料參數對波數虛部的影響規律,從而確定其選取的原則.依據以上理論對 γ 的影響因素進行研究,涉及到的WGA 的材料參數如表1 所示.

表1 WGA 的材料參數Table 1 WGA material parameters

研究分析了多個不同厚度比H時,損耗因子ηd對于 γ 的影響規律,其趨勢基本一致.H=5 的計算結果如圖3 所示,γ 隨 α 的增大先增大后減小,同厚度比下,γ 極大值對應的 α 不隨 ηd變化.相同 α 下γ隨 ηd的增加而近似線性地增加.彈性模量比 α 存在一個臨界值,當 α 小于臨界值,WGA 的抗彎剛度不隨Ed變化而顯著變化,振動由基材主導,但Ed增大顯著提高彎曲導致的應變能耗,導致波數虛部增大.當 α 超過臨界值,Ed的增大提高了梁的抗彎剛度,導致波數虛部降低.

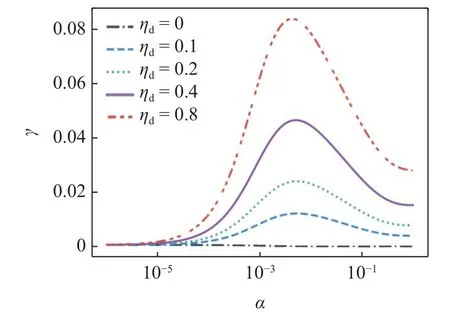
圖3 不同 ηd 下 γ 與 α 的關系(H=5)Fig.3 The relationship between γ and α under different ηd (H=5)

研究分析了多個不同 ηd時,厚度比H對于 γ 的影響規律,其趨勢基本一致.ηd=0.2 的計算結果如圖4 所示,隨著H的增加,γ 的極大值逐漸增大,且γ極大值對應的 α 逐漸減小.多數阻尼材料通常滿足α ≤1.0×10-3,當H>2 后,增加阻尼材料厚度對于γ的提升尤為顯著,此時增大H以提高彎曲波吸收效率具有更高的性價比,故 21.0×10-3)所需的最佳厚度較小,過厚的阻尼材料反而可能導致波數虛部降低.

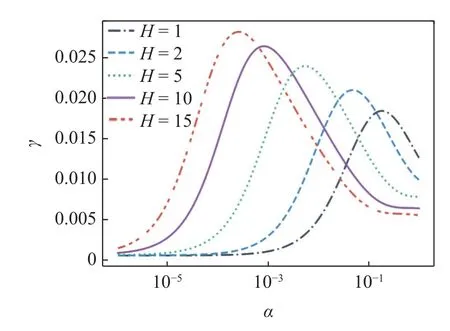
圖4 不同 H 下 γ 與 α 的關系(ηd=0.2)Fig.4 The relationship between γ and α under differentH(ηd=0.2)

以上研究表明,為保證以較短的尖端延伸長度實現彎曲波的吸收,首先應選用阻尼損耗因子盡可能大的阻尼材料,建議損耗因子不小于0.4.阻尼材料厚度的選取應依據彈性模量比來確定,低彈性模量的阻尼材料其厚度比宜取較大值,而高彈性模量的阻尼材料其厚度比取較小值.

1.3 幾何參數設計

在以往的研究中,ABH 的反射系數受到變厚度段厚度梯度相關的截止頻率[30](以下稱之為梯度截止頻率)的影響.而最近的研究表明,螺旋ABH 還受到螺旋線曲率相關的截止頻率[31](以下稱之為曲率截止頻率)的影響.當螺旋ABH 振動時,高于梯度截止頻率的彎曲波可在ABH 尖端內低反射地傳導,而高于曲率截止頻率的彎曲波可在曲梁內傳導.因此,當振動頻率低于任一截止頻率時,螺旋ABH 反射系數將接近于1,要獲得良好的彎曲波吸收效率,需確保兩截止頻率同時低于激勵頻率.

(1) 曲率截止頻率

對于螺旋的增強ABH,由于無法以解析解的形式給出曲率頻率,因此采用數值模擬的方式進行研究,數值仿真模型參數如表2 所示,阻尼材料彈性模量和損耗因子分別為200 MPa 和0.8.

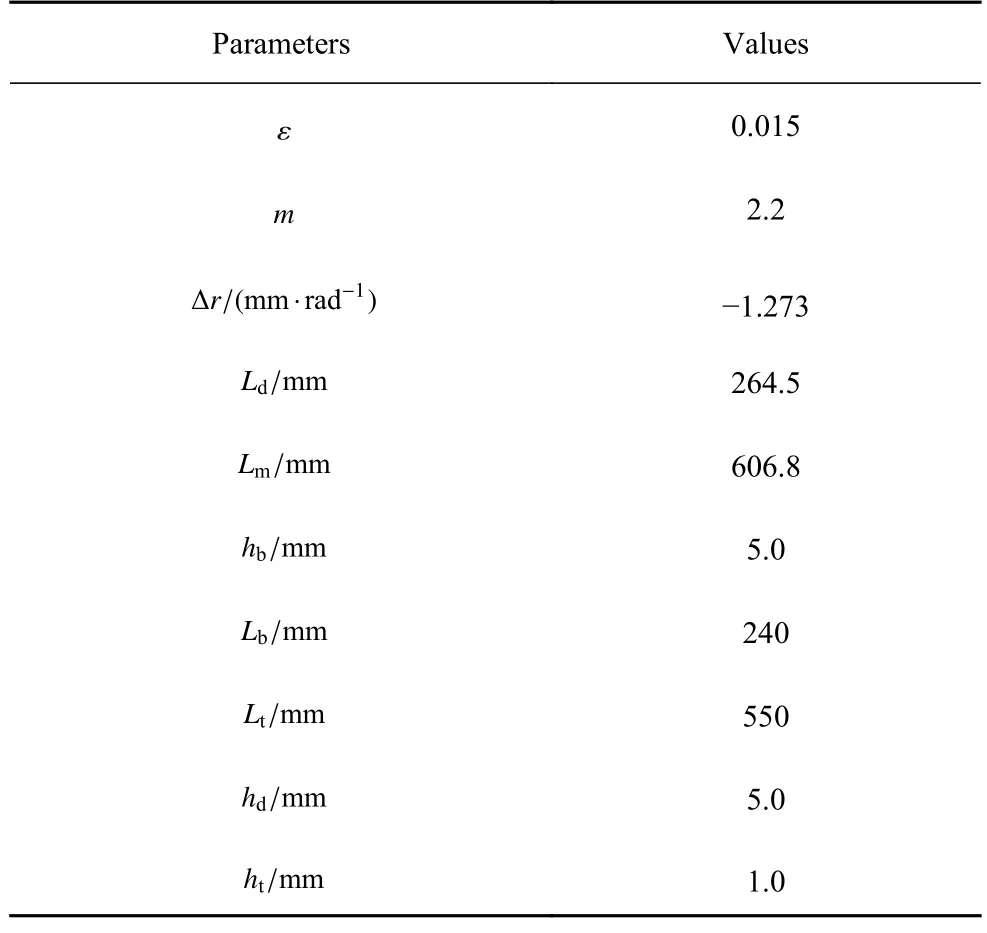
表2 WGA 幾何參數Table 2 WGA geometric parameters

按照Denis 等[32]的方法計算反射系數,結果如圖5 所示,橫坐標為與ABH 相連的直均勻梁的彎曲波波長 λb,縱坐標為螺旋線的最大半徑r0.云圖可大致劃分為左上與右下兩部分,其中右下部分滿足r0≤λb/12,在該區域內反射系數接近于1,以上現象與Lee 等的結論[31]一致:曲率截止頻率對應的波長(或波數)與螺旋線半徑(或曲率)近似為線性關系.設計WGA 時,應使r0≥λb/12 確保其曲率截止頻率低于目標減振頻率,進一步增大r0對于降低WGA的反射系數的作用較為有限.

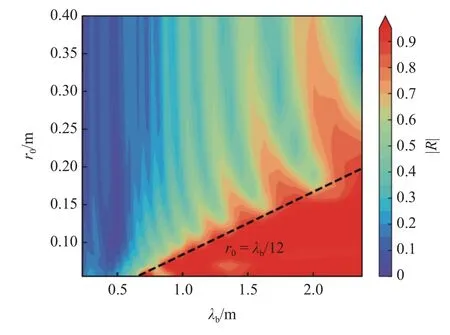
圖5 不同螺旋半徑下的反射系數Fig.5 Reflection coefficient under different spiral radii

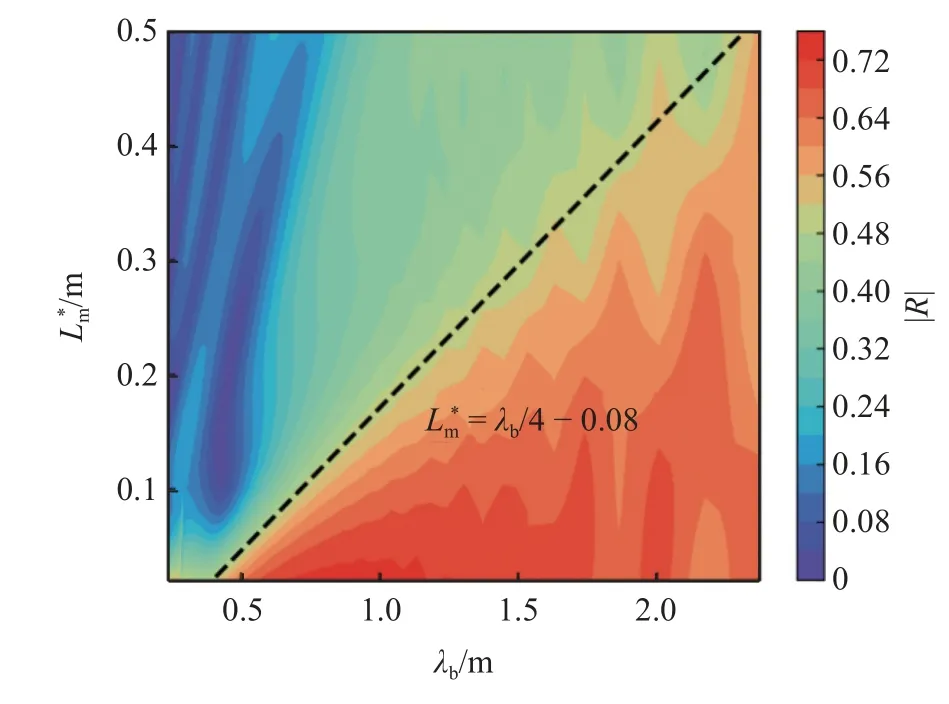
圖6 不同 長度下的反射系數Fig.6 Reflection coefficient under different

(2) 梯度截止頻率

經典ABH 的梯度截止頻率為[30]

將本研究中ABH 的幾何參數(表2)代入上式可得梯度截止頻率為23.3 Hz,由式(9)所描述的增強ABH 更易滿足低反射條件,實際梯度截止頻率低于上式的計算值.雖然上式無法給出準確的梯度截止頻率,但仍具有一定的指導意義,即降低基材彈性模量與密度的比值可降低WGA 的梯度截止頻率,然而調控基材的材料參數可能會導致WGA 與被減振結構間的阻抗不匹配,進而導致減振效果降低,相比之下調整幾何參數 ε,Lm和ht是更合理的方式.

為更準確地研究增強ABH 的梯度截止頻率,依據式(4)綜合考慮各幾何參數對于反射系數的影響,在Lm內差分計算式(4)的倒數

式中,λb是厚度為hb的均勻梁的彎曲波波長,λt是厚度為ht的延伸尖端的彎曲波波長.使用直ABH 模型計算反射系數從而排除曲率的影響,其余幾何參數如表2 所示.

2 仿真和實驗模型

2.1 WGA 模型

基于研究提出的設計方法,基材選用鋼,阻尼材料選用瀝青阻尼設計WGA,材料參數見表1,并測得阻尼材料的彈性模量和損耗因子分別為225 MPa和0.857,依據阻尼材料參數確定WGA 幾何參數如表2 所示,設計加工WGA 樣品并開展反射系數測量實驗與加筋板減振實驗.圖7 所示的用于加筋板減振實驗的WGA 與長度60 mm 的直梁相連,用于反射系數測量實驗的WGA 則與長度為240 mm 的直梁相連.

圖7 WGA 實驗模型Fig.7 WGA experiment model

2.2 加筋板模型

加筋板實驗模型如圖8 所示,材料為鋼,四邊固支.鋼板對稱軸處焊接有橫向和縱向兩條“L”形加強筋,加筋板總質量為57 kg.施加10～1000 Hz 的掃頻激勵,掃頻速率為2 Hz/s 測量加筋板振動響應,實驗儀器及其型號如表3 所示,激振器與加速度傳感器安裝在未焊接加強筋的一面,測點、激勵點以及WGA 的安裝坐標如圖9(a)所示.

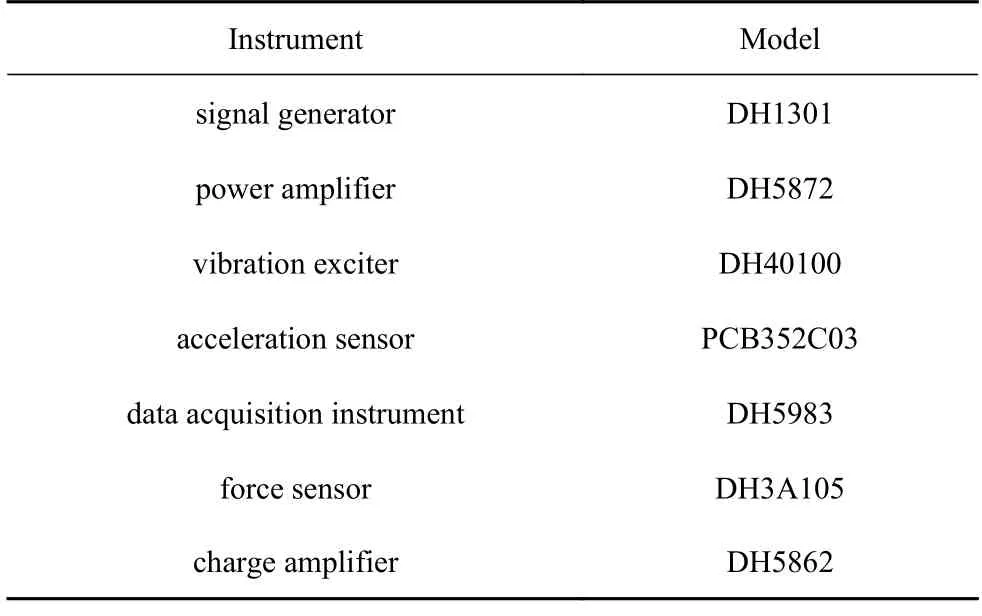
表3 實驗設備型號Table 3 Model of experimental equipment

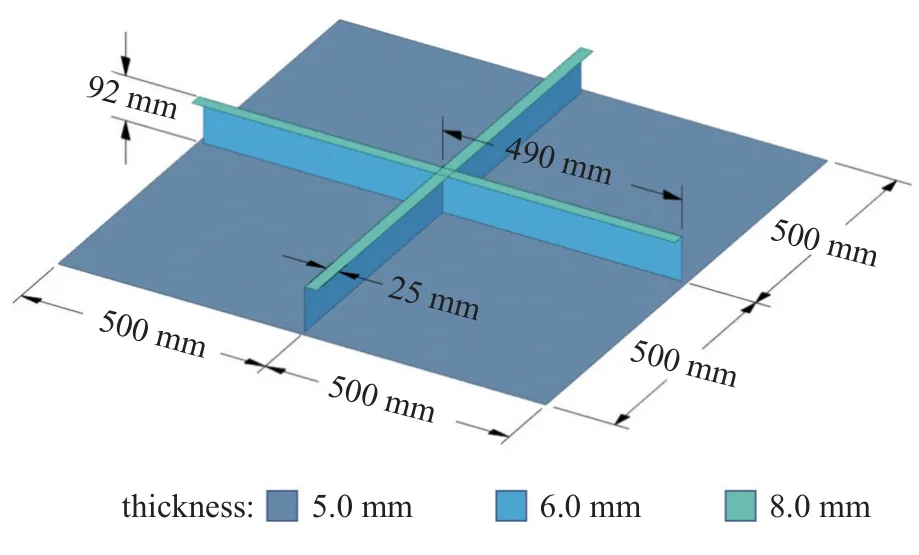
圖8 加筋板尺寸標注Fig.8 Dimensions of stiffened plates

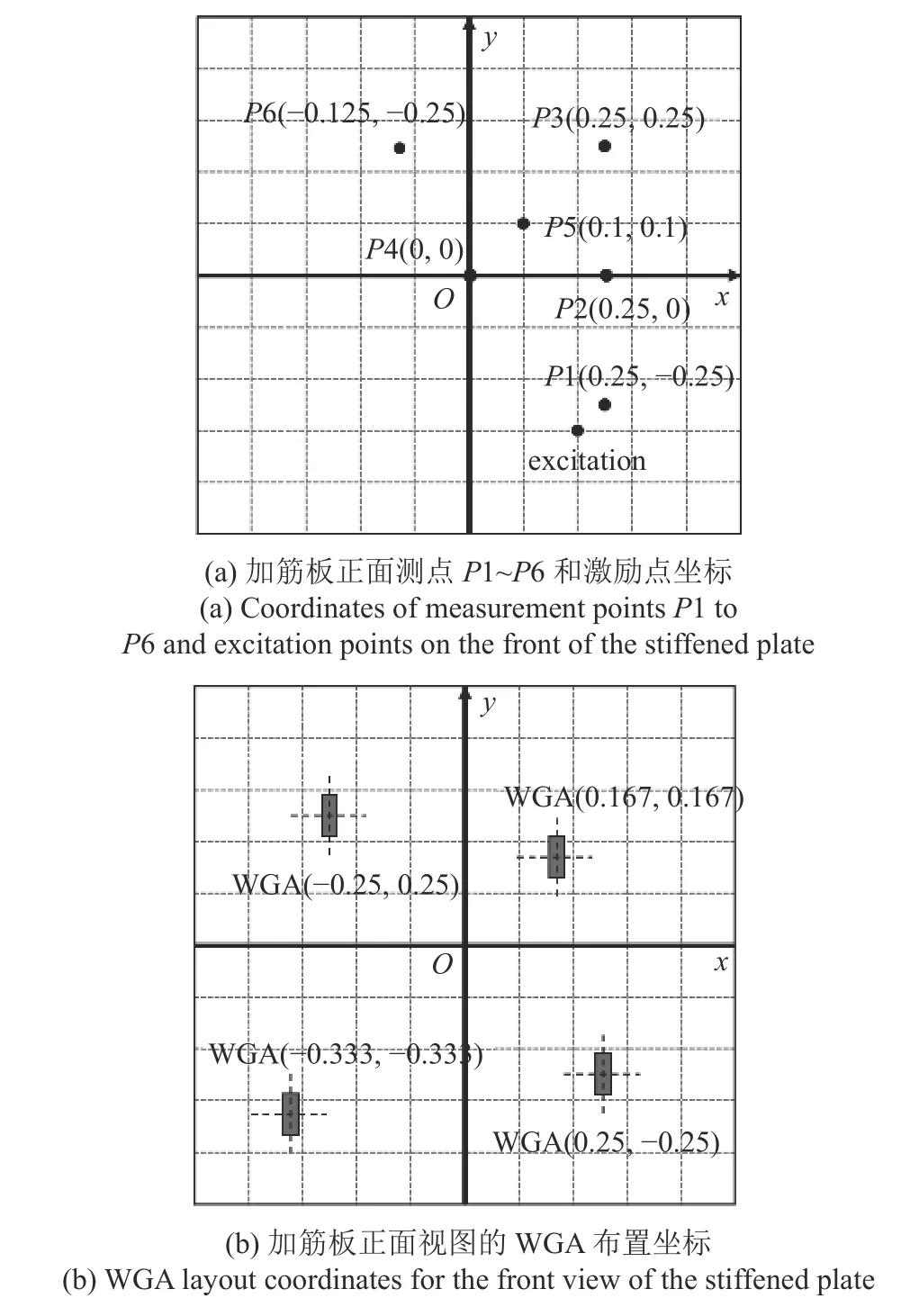
圖9 加速度測點布置和WGA 布置圖Fig.9 Schematic diagram of acceleration measurement point arrangement and WGA arrangement

共設計了10 組實驗.其中1 組未安裝任何元件作為參考;另外9 組分別為安裝1,2,4 個元件(阻尼層、質量塊或WGA)的實驗組.安裝數量為1 時,安裝位置為圖9(b)的右下角板格;當安裝數量為2 時,安裝位置為右側兩個板格.所有元件的單件質量均為0.76 kg.使用α-氰基丙烯酸乙酯膠水將WGA 或質量塊黏接于加筋板焊接有加強筋的一面,質量塊和WGA 與加筋板的黏接面面積相同,安裝位置也相同.阻尼層型號為TD09,厚度為2.2 mm,長和寬均為0.46 m,彈性模量和損耗因子分別是271 MPa和0.188.加工的加筋板實驗模型如圖10 所示,WGA和阻尼層布置分別如圖10 (c)和圖10 (d)所示.

圖10 加筋板和固支框架照片Fig.10 Photos of stiffened plates and fixed frames

3 結果與討論

3.1 WGA 反射系數分析

反射系數測量實驗如圖11 所示,激振器連接于直梁右側距端面10 mm 處,兩加速度傳感器分別固定于直梁上距端面110 mm 和130 mm 處.掃頻激勵并測得兩點加速度后計算反射系數.

圖11 WGA 反射系數測量實驗照片Fig.11 Photo of WGA reflection coefficient measurement experiment

反射系數測量結果如圖12 所示,藍色實線為尖端厚度為1.0 mm 的WGA,其曲率截止頻率約為130 Hz.在低于曲率截止頻率時反射系數接近1.0,而在高于曲率截止頻率時反射系數迅速降低至0.4 以下,在255 Hz 第1 次到達最低點0.12,之后輕微上升并在778 Hz 出現極大值0.31.圖中實驗與仿真結果基本吻合,說明數值仿真方法準確.

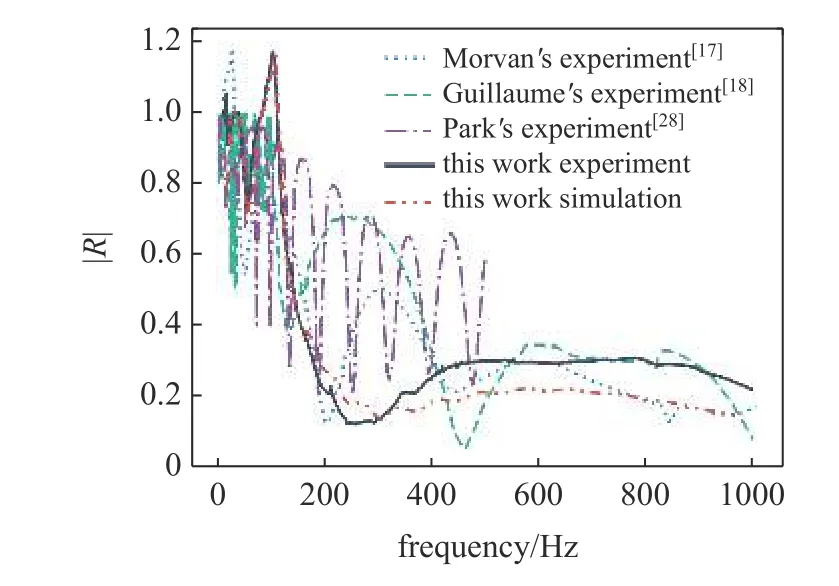
圖12 ABH 反射系數對比Fig.12 ABH reflection coefficient comparison

將結果與Morvan 等[17]和Guillaume 等[18]的研究對比,其研究中的ABH 尖端厚度為89 μm,本研究設計的WGA 在尖端厚度增大一個數量級的條件下,表現出更低的截止頻率,并在截止頻率以上的頻段內保持較低的反射系數.相對于Park 等[28]研究中構建的尖端厚度為0.5 mm 的WGA,本研究通過合理的阻尼參數和幾何參數調控設計,在尖端厚度為其兩倍的條件下,在141 Hz 以上頻段獲得了顯著更低的反射系數,驗證了設計方法的可靠性.

3.2 WGA 能量耗散機理分析

(1) 時域分析

在圖13 所示WGA 右端面施加幅值為0.1 mm的Ricker 子波脈沖激勵.脈沖從Ls=0.0 m 處發出,并在Ls=0.24 m 處進入WGA 的變厚度段,在Ls=1.36 m 處到達WGA 尖端.

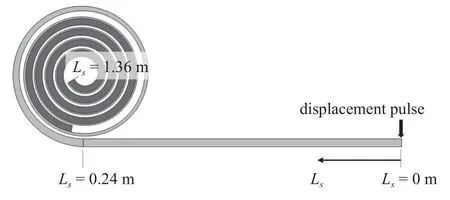
圖13 WGA 數值仿真幾何模型圖Fig.13 Geometric model diagram of WGA numerical simulation

計算對比了200,500 和1000 Hz 主頻的脈沖響應結果,三者波長不同,但傳導和耗散規律基本一致.以500 Hz 主頻脈沖為例,黏貼有阻尼材料和未黏貼阻尼材料的兩種WGA 脈沖位移響應如圖14 所示.0.0～3.91 ms,彎曲波在0.00 m≤Ls<0.58 m 的未黏貼阻尼材料段內傳導,幅值逐漸增大,波長和波速減小.3.91 ms 后,脈沖在未黏貼阻尼材料的WGA(圖14(a))中反復反射,能量無法被吸收,而在黏貼有阻尼材料的WGA (圖14(b))中彎曲波幅值快速下降至接近于0,無明顯反射.

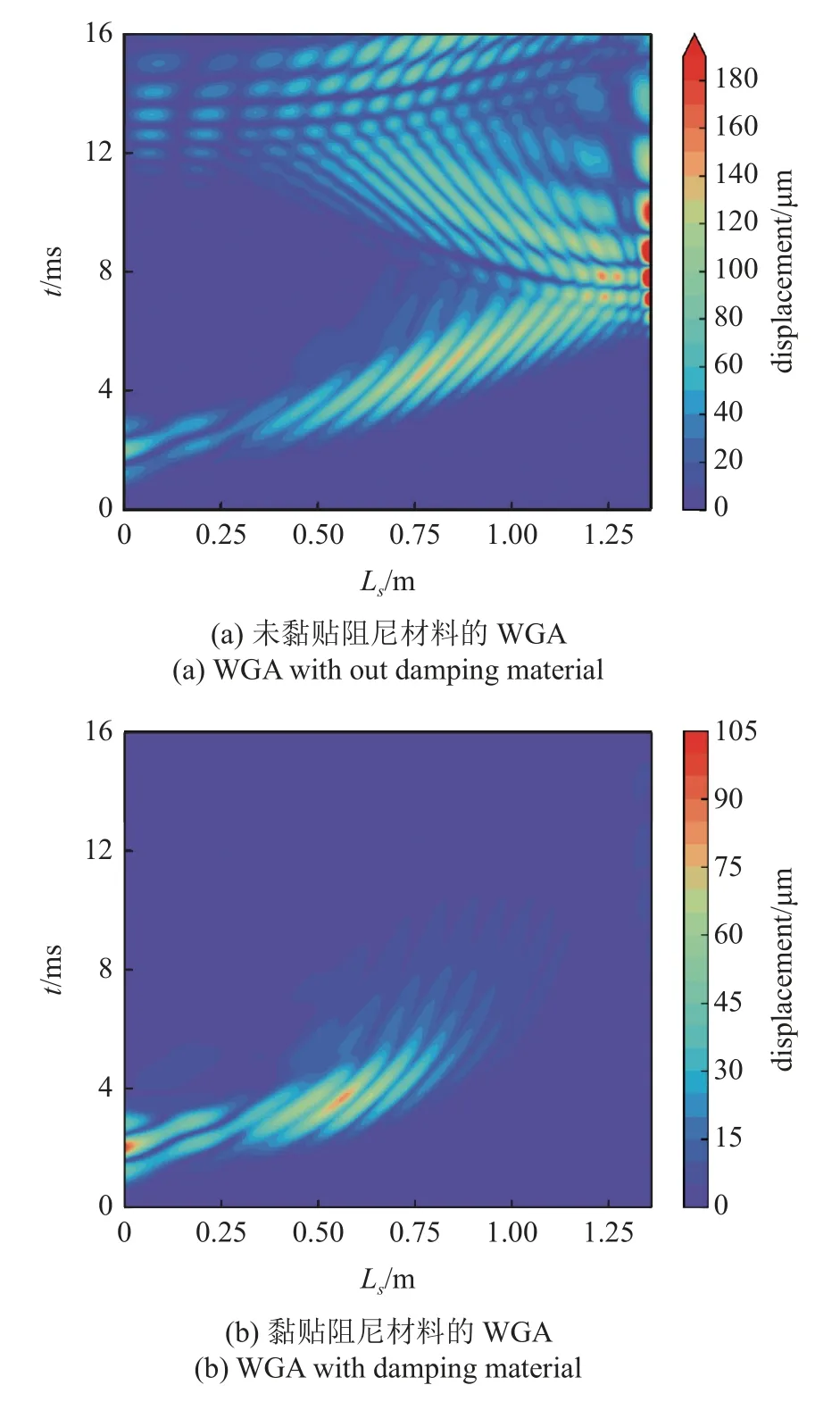
圖14 Ricker 子波脈沖的傳播和衰減Fig.14 Propagation and attenuation of Ricker wavelet pulses

(2) 頻域分析

計算模型如圖13 所示,施加1 N 的簡諧力,在10～1000 Hz 內對WGA 的能量耗散進行數值仿真,總功耗計算結果如圖15 所示,在曲率截止頻率以下的頻率,功耗曲線出現4 個明顯的吸收峰,對應頻率分別為17,20,41 和50 Hz.當頻率大于曲率截止頻率時,阻尼材料的熱耗散總功率始終保持在較大值,表明阻尼材料在寬頻范圍內實現了彎曲波的吸收.

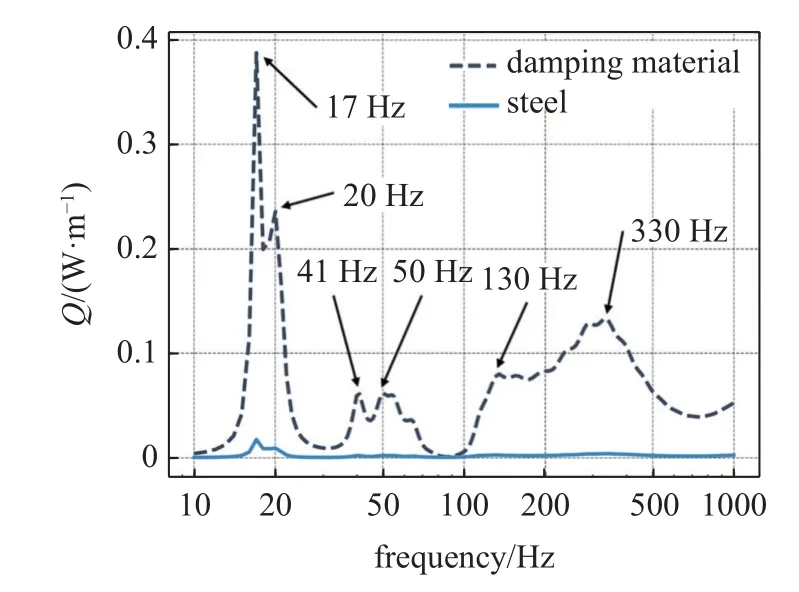
圖15 WGA 總功耗曲線Fig.15 WGA total power consumption curve

頻率為17 Hz 和41 Hz 的振型如圖16(a)圖16(c)所示,螺旋部分位移矢量與其所在螺旋線相切,WGA的轉動慣量與其作為螺旋狀彈簧的抗扭剛度耦合,形成了近似旋轉的單自由度的彈簧-質量共振系統.頻率為20 Hz 和50 Hz 的振型如圖16(b) 和圖16(d)所示,螺旋部分的位移矢量基本平行且方向一致,表明WGA 的內部作為一個整體,與外部形成近似平動的單自由度的彈簧-質量共振系統.以上現象表明,在低于曲率截止頻率時,WGA 依靠共振實現能量耗散.當頻率大于曲率截止頻率,以圖16(e)和圖16(f)的振型為例,螺旋部分的位移矢量與螺旋線垂直,且周期性地指向螺旋線內部或外部,表明WGA 的螺旋結構發生彎曲變形,彎曲波在WGA 內傳導和匯聚.

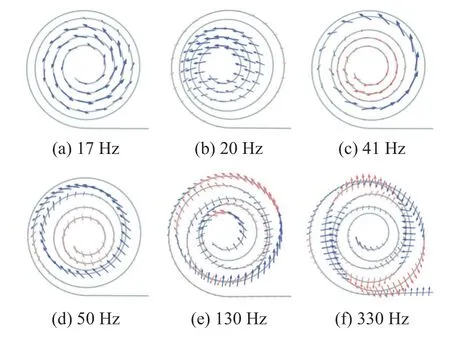
圖16 能量耗散峰值對應頻率的振動變形模式圖Fig.16 Vibration deformation mode diagram of corresponding frequency of energy dissipation peak

3.3 加筋板減振實驗結果分析

所有測點的加速度導納結果規律一致,選取測點P3 的加速度導納譜細節如圖17 所示,將其中各元件對加筋板的主要影響結果統計于表4 和表5 中.

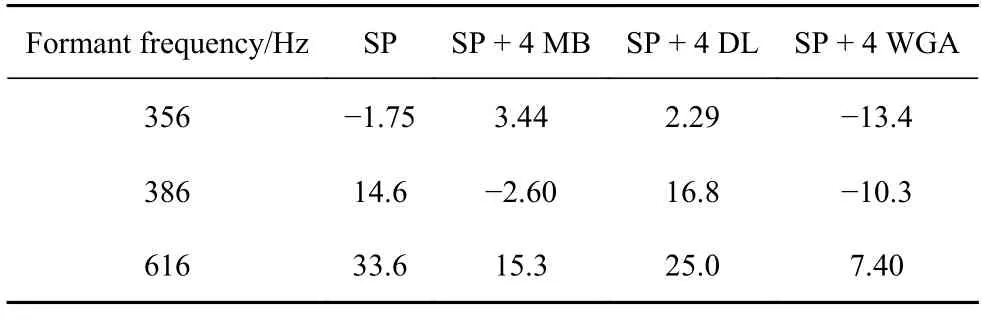
表4 共振峰加速度導納(dB)Table 4 Acceleration admittance of formant (dB)

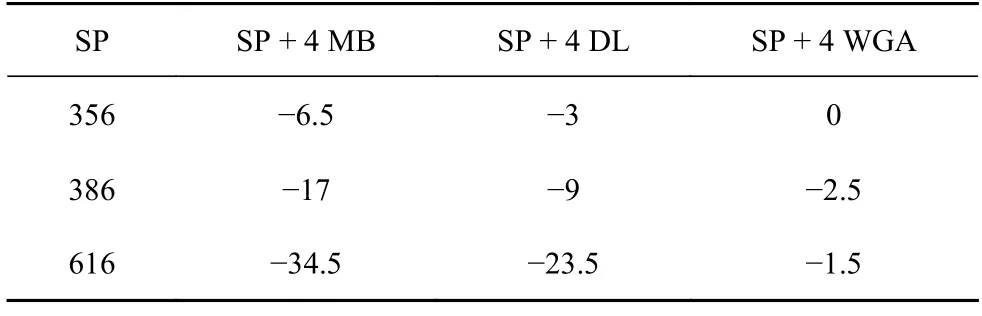
表5 共振峰頻率偏移量(Hz)Table 5 Formant frequency offset (Hz)

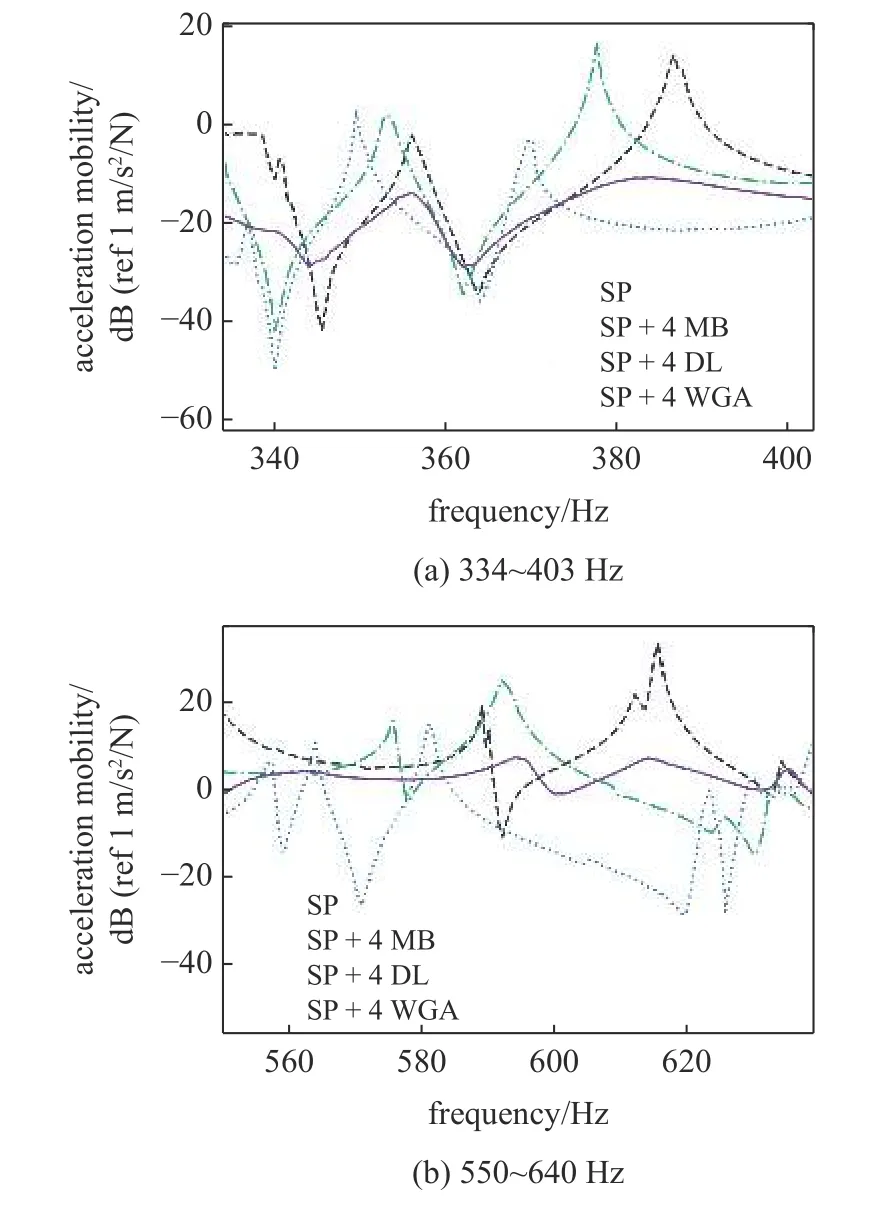
圖17 測點P3 的加速度導納細節Fig.17 Acceleration admittance details of measurement point P3

表4 為測點P3 在未安裝任何減振元件的加筋板(stiffened plate,SP),以及安裝有質量塊(mass block,MB)、阻尼層(damping layer,DL)和WGA 的加筋板在部分共振峰下的振動加速度導納結果,其中安裝WGA 后加筋板的加速度導納顯著低于其余三者,減振效果明顯,其中616 Hz 的共振峰加速度導納降低可達26.2 dB.

表5 為安裝各減振元件后的共振峰偏移量,其中安裝質量塊后加筋板共振頻率變化最為明顯,而WGA 在顯著降低共振峰加速度導納的同時,被減振結構共振頻率變化不超過2.5 Hz,對于結構自身振動特性的影響更小,原因是WGA 基本不改變加筋板的結構剛度,且其大部分質量不直接參與加筋板振動.

WGA 在所有測點均表現出了顯著優于阻尼層的減振效果,圖18 為測點P1 和測點P3 的加速度導納譜.安裝WGA 后,加筋板受到了明顯的阻尼作用,其加速度導納曲線更加平滑.常規阻尼層的減振效果隨頻率的升高逐漸提高,而WGA 對于加筋板的幾乎所有共振峰均產生了明顯的抑制.在較高頻段,質量塊同樣能顯著降低共振峰值,原因是其慣性力抑制了加筋板的振動.

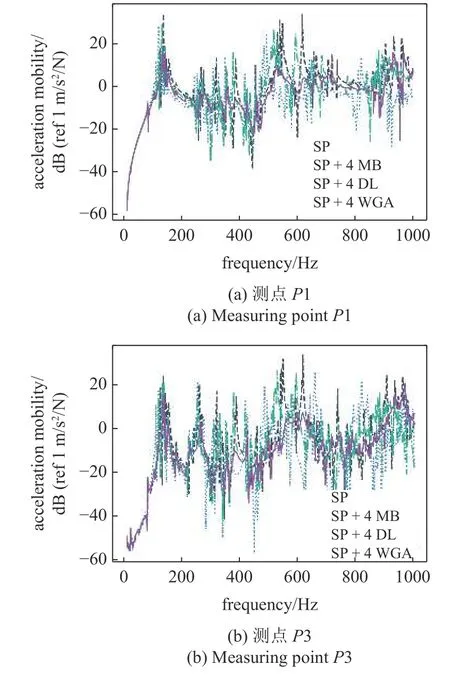
圖18 各個測點的加速度導納Fig.18 Acceleration admittance of each measuring point

以上研究表明,WGA 構型實現了彎曲波的匯聚和能量耗散,中低頻段振動抑制效果顯著優于等質量的常規阻尼層和質量塊.

4 結論

(1)研究提出了WGA 的設計方法,從理論上給出了降低反射系數和截止頻率的調控策略.阻尼材料損耗因子應盡量大,阻尼材料厚度應依據彈性模量比來確定,且其厚度應大于延伸尖端厚度的2 倍,WGA 的半徑不小于目標減振頻率彎曲波波長的1/12.

(2)WGA 在低于曲率截止頻率時通過共振耗散能量,在高于曲率截止頻率時,通過彎曲波的傳導而耗散能量,表現出寬頻減振特性.

(3)WGA 在寬頻范圍內具有良好的減振性能,其對于加筋板結構的減振效果顯著優于等質量的常規阻尼,且WGA 對被減振結構的振動固有特性的影響很小.