空氣-懸浮液驅替條件下顆粒邊壁滯留研究1)

李東奇 楊志兵 張 樂 胡 冉 陳益峰

* (華北水利水電大學水利學院,鄭州 450046)

? (武漢大學水資源工程與調度全國重點實驗室,武漢 430072)

** (華北水利水電大學河南省水圈與流域重點實驗室,鄭州 450046)

引言

氣(液)-液-顆粒多相流動是諸多自然與工業生產中的重要物理過程,例如:甲烷釋放[1-2]、油氣與礦產資源開采[3-6]、污染物運移與修復[7-8]、CO2地質封存與利用[9-11]、材料涂層制作[12-13]、制藥與藥物傳輸[14-15]等.氣-液或非混溶液-液兩相流作為多相流的基礎,首先得到了國內外學者的廣泛關注,其主要研究界面形態演化的控制機制,例如,驅替模式相圖[16-17]、黏性指進流的生長與抑制[18-19]、介質濕潤性誘發的角流與優勢指流[20-21],以及液滴分流控制[22].當流體中存在固體顆粒時,如巖石侵蝕破裂的碎屑、流體與介質反應產生的結晶、污水排放的微塑料以及油氣壓裂開采使用的支撐劑等情形[23-29],此時氣-液-顆粒多相流動過程受流體間驅替流動、顆粒運動遷移、邊界幾何結構等共同控制.

室內可視化實驗觀測是目前研究氣-液-顆粒多相流動規律的主要技術手段.以經典Hele-Shaw 模型(平行板模型)為研究對象,Chevalier 等[30]和Sandnes等[31]分別研究了不同顆粒濃度和密度、流速條件下多相流驅替模式的轉變,其結果表明顆粒不同的運移行為使流動驅替表現出指進、迷宮或珊瑚等結構圖案.Li 等[32]的研究,發現了不同流速條件下顆粒存在沉降、懸浮和滯留3 種運移行為,并基于受力平衡分析與液膜理論,提出了顆粒運移行為判別準則.當僅關注顆粒的滯留問題時,目前研究多以開展浸涂(dip-coating)實驗為主,即在充滿顆粒懸浮液的水槽中提升固體板,隨著提升速度的增加顆粒會滯留在固體表面上,從而形成了周期性條狀或均勻密實等涂層結構[12-13],其也被稱為對流自組裝技術(convective self-assembly).Colosqui 等[33]基于格子玻爾茲曼方法模擬了dip-coating 過程中氣-液界面的形態與顆粒的運動特性,揭示了顆粒在液體薄膜中的成簇滯留機制.Gans 等[34]、Sauret 等[35]和Palma 等[36]基于實驗研究了提升速度、顆粒粒徑和濃度對滯留行為的影響,并揭示了dip-coating 過程中顆粒的不同滯留模式.上述研究結果均表明顆粒的滯留行為與固體邊壁上液膜的厚度密切相關.但液體的膜厚不僅與流體性質、流速有關,還受到流動邊界的幾何形狀影響.為此,Jeong 等[37]和Wu 等[38]分別在圓形和矩形微通道中開展了空氣驅替顆粒懸浮液的實驗,研究了微通道中顆粒的滯留行為.多相流驅替過程中顆粒的滯留機制對揭示材料表面改性[35]、顆粒污染物運移[37-38]、通道的淤積堵塞[25,39]等方面具有重要意義.

上述實驗與理論研究成果豐富了對顆粒滯留問題的認知.但不同流動通道結構中流場特征、彎液面形狀與流動驅替模式有著顯著的區別,對于具有一定間距的平行板流動構型(Hele-Shaw 模型)中顆粒滯留問題尚未得到充分的研究,其顆粒滯留的形態特征及控制機制仍不明晰.為此,本文基于自主搭建的多相流可視化實驗裝置,在經典Hele-Shaw 平行板模型中開展了空氣驅替顆粒懸浮液的可視化實驗,探究了不同流量、板間距和顆粒粒徑條件下顆粒的滯留行為,發現了顆粒無滯留、顆粒成簇滯留及顆粒均勻分散滯留3 種模式.在實驗的基礎上,結合液膜理論和氣-液界面處流場特征分析,推導建立了顆粒滯留的判別準則,揭示了受毛細數和間距粒徑比控制的顆粒滯留行為機制,并與實驗結果對比驗證了模型的有效性.

1 實驗方法

1.1 多相流可視化實驗裝置

自主研發了多相流可視化實驗裝置,如圖1 所示.該裝置主要由矩形Hele-Shaw 模型、注射泵、相機和光源等組成.其中,矩形Hele-Shaw 模型由琉璃材質的透明長方體板、塞尺、止水夾板、進出口槽和金屬外框架組合而成,兩板的間距b0由塞尺的厚度決定.模型組裝后的有效觀測區域的長度L為100 mm,寬度W為13.2 mm,板間距b0等于塞尺的厚度(1,1.5,2 和3 mm).矩形Hele-Shaw 模型的幾何結構固定,且流體的流動方向單一,因此常常作為基礎研究的實驗對象.

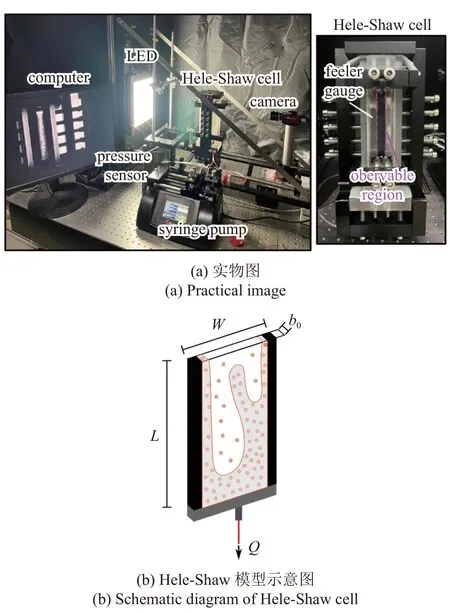
圖1 多相流可視化實驗裝置Fig.1 Multiphase flow visualization system

Hele-Shaw 模型通過四氟乙烯管(內徑2.5 mm,外徑3.5 mm)與注射器(Hamilton,5～50 mL)相連,流體流動由高精度注射泵(Harvard 703007,注射體積精度 ±0.25%)驅動.根據實驗設計,可實現注入/抽取流量從0.01 mL/min 到20 mL/min 的恒流量條件.流動模型豎向放置,在流動模型的前側及后側分別放置科研級相機(AVT,manta G-1236C)和LED面光源,相機的采集幀率為10 幀/s,采集圖像的分辨率為57.4 μm.

1.2 材料物理性質

實驗在常溫環境(20 ± 0.5 °C)中開展,入侵相為空氣(黏度和密度均可忽略),被驅替相為顆粒懸浮液.懸浮液中液相為二甲基硅油(阿拉丁),顆粒采用單分散聚乙烯非熒光顆粒(Cospheric Inc),兩者密度基本相同.二甲基硅油對琉璃壁面和聚乙烯顆粒為強濕潤性[40],因此顆粒可以均勻地分散于硅油中.如圖2 所示,基于液滴形狀分析儀(Kruss,DSA25)測試了純硅油與顆粒懸浮液對于本實驗琉璃材質模型的接觸角,其靜態接觸角小于10°,且液體中顆粒存在對接觸角不產生影響.實驗中采用粒徑為180～212 μm 的顆粒,即懸浮液SUS-196.顆粒密度為ρp=0.98 g/cm3,懸浮液中顆粒的體積分數(濃度)均為?≈ 20%.硅油黏度為μf=200 mPa·s,密度為ρf=0.97 g/cm3,界面張力為σ=21 mN/m.

圖2 接觸角測量Fig.2 Contact angle measurements

1.3 實驗步驟及圖像后處理

按照實驗設計配置顆粒懸浮液,然后將懸浮液以5 mL/min 的流量注入模型,使其充滿.隨后,固定抽取流量開始實驗,通過相機記錄整個驅替過程的圖像.當驅替界面達到可觀測區域底部時,實驗結束,并記錄從開始至結束的時間為突破時間tbt.在實驗結束后,通過超聲波、等離子清洗機、酒精和超純水對模型進行清洗.

通過自編譯的MATLAB 程序對灰度圖像進行二值化處理,并采用中值濾波方法過濾圖像中的噪點.為了定量評價顆粒的滯留程度,本文定義了顆粒滯留系數,其可表示為

式中,Sdep為顆粒滯留系數,Ainv和Ap分別為突破時刻入侵相(空氣)和滯留顆粒相所對應的二值化平面面積.

此外,指進尖端速度是計算毛細數Ca、雷諾數Re等中的重要參數.通過對一組驅替過程圖像的二值化處理,可得到一個時間步Δt內尖端距離的變化值ΔLtip,從而求得該時間步內的平均速度為

將該平均速度與根據實驗設定流量求得的速度進行對比,兩者結果基本相同,驗證了本文實驗控制與圖像后處理技術的有效性.

2 實驗結果分析

2.1 空氣-懸浮液驅替模式

圖3 首先給出了3 種不同的空氣驅替懸浮液流動過程,其中空氣為非濕潤驅替相,而顆粒懸浮液為被驅替相,氣-液界面從上向下推進.當兩板間距一定時,在小流量條件下界面平直推進,被驅替的濕潤相在邊壁上殘留一層液體薄膜,驅替過程基本為完全驅替,即表明驅替處于在毛細力和重力主導的穩定模式,如圖3(a)所示.殘留的液體薄膜為顆粒滯留的發生提供了必要條件;隨著流量的增加,驅替界面仍基本平直,驅替為穩定模式,但殘留的液體膜厚增大;當液體膜厚達到一定條件時,顆粒滯留發生,如圖3(b)所示.當流量進一步增大時,不穩定黏性指進出現,驅替處于黏滯力主導的不穩定模式,且伴隨著更加均勻的顆粒滯留,如圖3(c)所示.

圖3 板間距1.5 mm 條件下空氣-懸浮液驅替模式Fig.3 Gas-suspension displacement patterns at gap 1.5 mm

2.2 不同實驗條件下顆粒的滯留模式

為了分析顆粒的滯留行為,系統開展了不同板間距、流量條件下的空氣-懸浮液驅替流動可視化實驗,如圖4 所示.為了進一步定量評價顆粒的滯留程度,根據式(1)計算了不同實驗條件下顆粒滯留系數,如圖5 所示.當顆粒不發生滯留時,滯留系數Sdep為0.當顆粒發生滯留后,Sdep整體上隨著板間距的增加而增大;而在相同板間距的條件下,隨著流量的增加,Sdep表現為先快速增大而后趨于穩定(緩慢增加或略微減小)的變化趨勢,即反映了氣-液驅替過程中顆粒存在不同的滯留模式,此時滯留系數Sdep的變化趨勢與顆粒滯留模式有關.

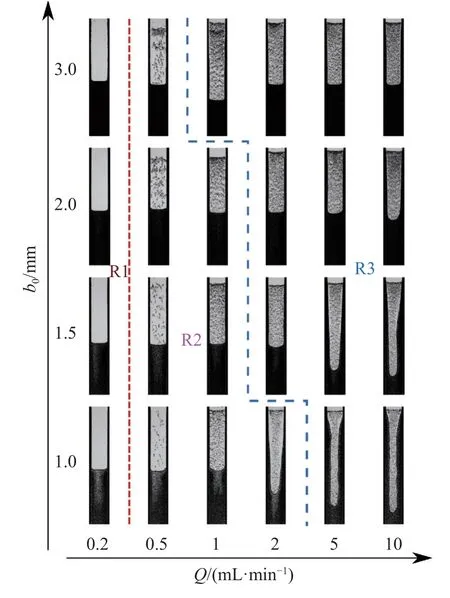
圖4 不同板間距、流量下顆粒滯留實驗相圖Fig.4 Experimental phase of particle deposition under different gaps and flow rates

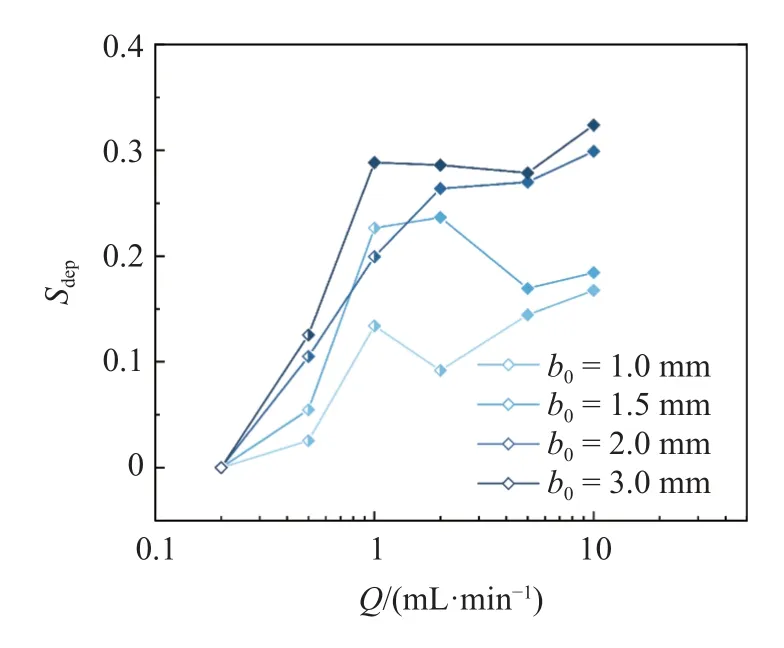
圖5 滯留顆粒體積分數Fig.5 Volume fraction of deposited particles

如圖6(a)所示,當流量較小時,顆粒聚集成團簇來抵御界面的毛細過濾作用,即顆粒滯留表現為團簇滯留形態.隨著流量的增加,殘留的液體薄膜亦增加,毛細過濾作用減弱,顆粒以單個分散或小團簇形態滯留,此時Sdep隨著流量的增加而快速增加.如圖6(b)所示,隨著流量的進一步增加,毛細過濾作用基本消失,此時顆粒滯留主要表現為均勻分散的滯留形態,Sdep基本趨于穩定.

圖6 顆粒滯留局部放大圖,板間距為3 mmFig.6 Enlarged view of particle deposition at gap 3 mm

根據圖4 的結果,結合顆粒滯留形態分析,將顆粒滯留劃分為3 種模式,即顆粒無滯留(R1)、顆粒成簇滯留(R2)以及顆粒均勻分散滯留(R3).圖4 中紅線和藍線分別為滯留模式R1,R2 和滯留模式R2,R3 的分界線,而在圖5 中空心、半實心和實心符號分別代表3 種滯留模式R1,R2 和R3.從圖4 中可以看出,顆粒滯留行為與板間距、流量等因素均有關.首先,在一定開度條件下,隨著流量的增加,顆粒從無滯留模式向成簇滯留模式、均勻分散滯留模式轉變.其次,顆粒均勻分散滯留的臨界流量隨著板間距增大而減小,即流量越大、板間距越大,顆粒越易發生滯留.隨后,本文基于液膜理論和流場分析建立顆粒滯留的判別準則,并與實驗結果對比,來驗證判別準則的有效性,并最終揭示顆粒滯留的控制機制.

3 理論分析

3.1 懸浮液等效黏度

顆粒與周圍流體的相互作用決定了懸浮液的表觀(等效)黏度,其主要與流體黏度和顆粒濃度有關,具體可表示為[41]

式中,μequ為懸浮液的等效黏度,μf為懸浮液中液體的黏度,?為懸浮液中顆粒的體積分數,?max為顆粒填充的最大體積分數,一般取?max=0.62[30,42].在本次實驗條件下,根據式(3),可求得顆粒懸浮液的等效黏度為352.2 mPa·s.

3.2 殘留液膜厚度

在不混溶兩相(如氣-液兩相)排水驅替過程中,被驅替的濕潤相會在邊壁上殘留一層液體薄膜,這為顆粒滯留的發生提供了必要條件.薄膜的厚度與流體的性質、通道的幾何尺寸和界面速度有關,其取決于黏滯力、毛細力、重力之間的競爭.本文實驗中重力相對于毛細力的作用較小(邦德數Bd=ρfgb02/(4σ) ≤ 1),此時理論模型中可暫不考慮重力對彎液面形狀和薄膜厚度的影響[43].當毛細數Ca遠小于1 時,1961 年Bretherton 首先建立了薄膜厚度hfilm與毛細數Ca和流動通道之間的關系.當氣體驅替牛頓流體時,文獻[37,44]根據大量的實驗數據,在Bretherton 模型的基礎上提出了可適用毛細數Ca≤2 的經驗公式,其可表示為

式中,毛細數為Ca=μequvtip/σ,其中尖端速度vtip和等效黏度μequ分別根據式(2)和式(3)求得.需要說明的是,當Bd較大且重力對彎液面形狀有較大影響(如Hele-Shaw 模型水平放置)時,薄膜厚度hfilm為毛細數Ca與邦德數Bd的函數[43,45].

3.3 顆粒滯留的判別準則

在液膜理論的基礎上,進一步分析驅替界面后流場特征與顆粒運動,從而提出顆粒滯留的判別準則.如圖7 所示,當液體薄膜存在時,驅替界面后的渦旋流場可分為兩個區域,即流體流入薄膜的區域Ω1和主體內的渦旋流區域Ω2.顆粒滯留發生的過程為顆粒首先進入了Ω1區域并與氣-液界面產生接觸,逐漸使界面產生變形,最終被夾帶在液體薄膜中.此時,顆粒滯留主要由界面毛細力(FC)、流體拖曳力(FD)和底部摩擦力(Ff)之間的競爭控制,其中拖曳力為驅動力,而毛細力為阻礙力.而當顆粒在Ω2流動區域時,顆粒會循環到被驅替液體中或與界面接觸產生擾動,但不發生滯留.因此,顆粒滯留發生的關鍵在于顆粒能夠進入Ω1流動區域,此時流動區域Ω1和Ω2的分界點位置為關鍵參數.如圖7(a)所示,本文將該分界點定義為界面駐點,該點距邊界的高度定義為h*.基于潤滑理論,可求得h*為[33]

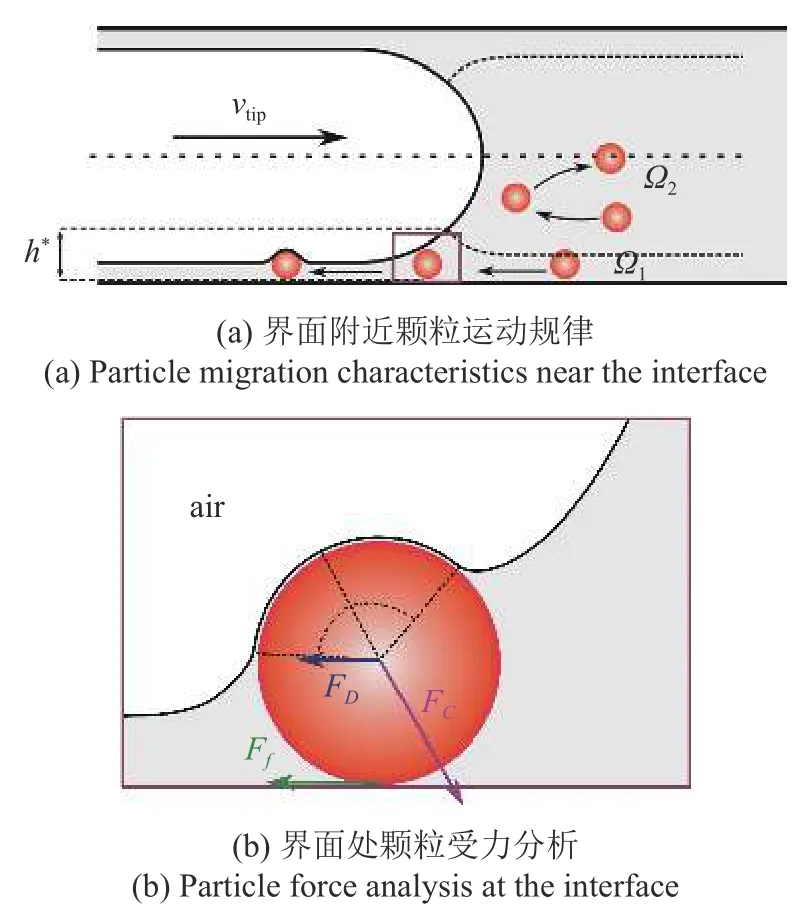
圖7 顆粒滯留示意圖Fig.7 Schematic diagram of particle deposition behavior

式中,lcap為表征流體所受表面張力與重力相對大小的毛細長度,lcap=[σ/(ρg)]1/2.一般情況下,薄膜厚度hfilm遠小于毛細長度lcap,因此上式可取h*≈ 3hfilm.基于上述分析,進一步提出顆粒滯留的幾何判據為

式中,Rp為顆粒的半徑;α為滯留幾何系數,反映了顆粒滯留發生時顆粒粒徑與界面駐點液膜厚度的關系.其中,α=1 是顆粒沿著流線進入區域Ω1的臨界條件,因此為顆粒滯留的下邊界條件.當α=2 時,顆粒進入薄膜區域Ω1后不會使界面變形,此時界面對顆粒的毛細阻礙力為0,因此為顆粒滯留的上邊界條件[37].

結合式(4)、式(5)和式(6),可最終推得顆粒滯留發生的臨界毛細數Cadep,即顆粒滯留的判別準則可表述為

3.4 結果對比

如圖8 所示,將圖4 中不同流量和板間距條件下空氣驅替顆粒懸浮液的實驗結果歸納到以毛細數Ca和間距粒徑比b0/Dp為橫、縱坐標的相圖中,并根據式(7)求得判別顆粒滯留的理論曲線.圖8 中方形符號、圓形符號和三角形符號分別代表3 種顆粒滯留模式的實驗結果,紅色和藍色虛線分別為α=1和α=2 時的理論曲線.從圖中可以看出,下邊界條件α=1 準確地捕捉了顆粒滯留的發生,因此可作為顆粒發生滯留的臨界判別條件.上邊界條件α=2 準確地預測了顆粒成簇滯留(R2)向顆粒分散均勻滯留(R3)的轉變,此時界面的毛細過濾作用基本消失,即顆粒可以無阻礙地滯留在液膜中.因此,上邊界條件α=2 可作為顆粒均勻滯留的臨界判別條件.此外,我們同樣開展了不同粒徑條件(355～425 μm)下空氣-懸浮液驅替實驗,結果表明其滯留行為隨流量和板間距的變化具有相同演變規律,且同樣可基于本文理論曲線預測;在相同板間距條件下小粒徑顆粒發生滯留的臨界流量更小,即小粒徑顆粒更易滯留.由于分析內容重復,文中不再過多闡述.

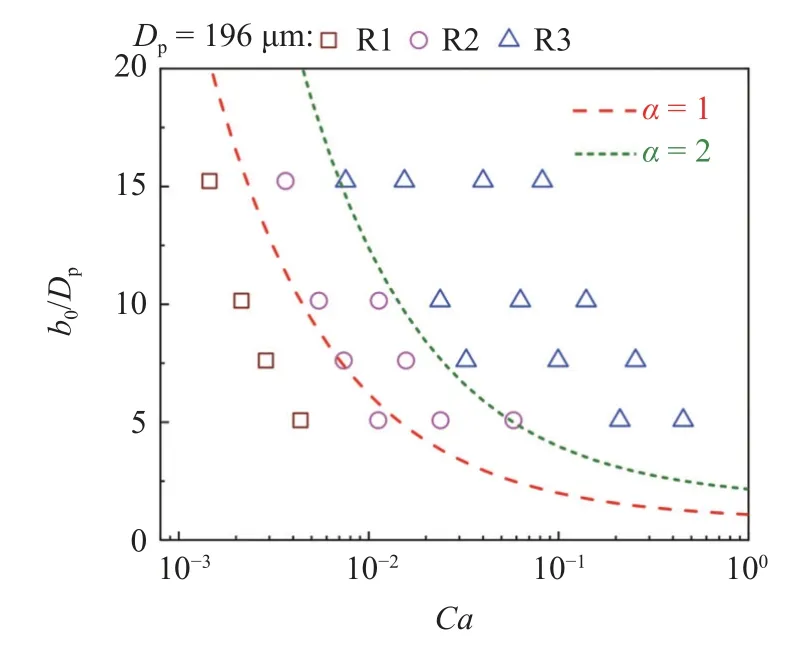
圖8 顆粒滯留行為的實驗與理論結果對比Fig.8 Comparison between experimental and theoretical results of particle deposition

綜上所述,理論結果與實驗結果吻合較好,即表明了理論模型的有效性.根據理論模型可以得出,顆粒滯留行為由流體性質、流速、板間距和顆粒粒徑等因素共同決定,其可歸結于通過毛細數Ca和間距粒徑比b0/Dp進行調節控制,從而揭示了顆粒滯留行為的控制機制,這為今后的工程實踐提供了重要的理論基礎.

4 結論

本文基于自主研發的矩形Hele-Shaw 模型-注射泵-相機多相流實驗裝置,系統開展了不同流量、板間距和顆粒粒徑條件下空氣驅替顆粒懸浮液的可視化實驗,并結合理論分析,研究了驅替過程中顆粒的滯留行為.本文得到主要結論如下.

(1) 在空氣-懸浮液驅替流動過程中,驅替界面存在穩定和指進不穩定模式,并可伴隨顆粒滯留的發生.

(2) 根據滯留形態特征,將顆粒滯留劃分為無滯留、成簇滯留及均勻分散滯留3 種模式,其與板間距、流量、顆粒粒徑等因素有關.隨著流量的增加、板間距的增大或粒徑的減小,顆粒從無滯留模式向成簇滯留模式和均勻分散滯留模式轉變,即流量越大、板間距越大以及粒徑越小,顆粒越易滯留.

(3) 邊壁上殘留的液體薄膜為顆粒滯留的發生提供了必要條件.基于液膜理論和氣-液界面處流場特征分析,提出了顆粒滯留的判別準則,并與實驗結果進行了對比驗證.該準則揭示了受毛細數和間距粒徑比控制的顆粒滯留機制,為實現顆粒運移控制提供一定的理論基礎.