基于響應面分析法的多通道烘缸換熱性能分析與參數優化

董繼先, 郭浩增, 王 莎, 喬麗潔, 王 博, 劉 歡

(1.陜西科技大學 機電工程學院, 陜西 西安 710021; 2.西安航空職業技術學院 自動化工程學院, 陜西 西安 710089; 3.陜西科技大學 材料科學與工程學院, 陜西 西安 710021)

0 引言

烘缸是造紙工業中重要的設備之一,對于提高烘缸的換熱效率這一問題,提升烘缸內部的冷凝水排放是一個重要的解決方案,為此,多通道烘缸這一烘缸結構被提出[1],并于后續的研究中進行了優化[2,3],具體結構如圖1所示,其目的在于利用蒸汽壓力排出烘缸內部的大部分冷凝水,并在后續的研究中,多通道烘缸在換熱性能提升的優勢得到了證實[4].

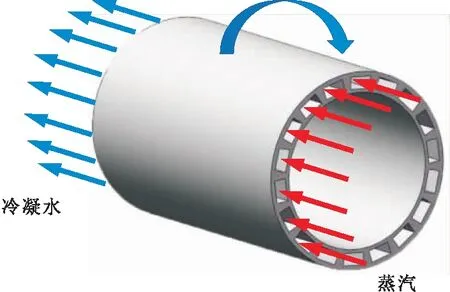
圖1 多通道烘缸結構示意圖

對于多通道烘缸的研究方面,由于烘缸實際工作的狀態為繞水平軸線轉動,研究難度相對較大,因此部分學者首先基于靜止狀態下烘缸進行了實驗研究.Yan Y等[5]對靜止狀態下多通道烘缸矩形水平流道的流形進行了研究,得出在未轉動的條件下,低質量流速出現塞狀流、波狀流等流形,而高質量流速下則是環狀流和波狀流為主而沒有出現塞狀流,其流型與已有的流型圖基本一致,并得出了與實驗吻合較好的已有的換熱和壓降關聯式;隨后又對不同的通道結構參數對烘缸換熱特性的影響進行了研究[6],得出多通道烘缸的建議通道數量為150～200,橫截面長寬比為1∶3,間距比為1∶1～1∶3時,烘缸的整體換熱性能最佳.喬麗潔等[7,8]則對靜止狀態下多通道烘缸流道冷卻參數對換熱性能的影響進行了研究,得出蒸汽質量流速增大或用于模擬濕紙幅的冷卻水質量流量增大時,烘缸的整體的換熱系數都會提升,但隨著冷卻水質量流量的增大,換熱系數出現了波動,因此增大蒸汽質量流速是實現換熱效果提升的較好方案;后續又對通道內的壓降情況分別用分相流和均相流模型予以研究[9],結果表明均相流模型不適用于通道內壓降的計算,并篩選出了相對較好的壓降契合模型;并對U型截面通道的流型分布情況和流動特性進行了研究[10],得出環狀流出現的最佳正其質量流量與冷卻水質量流量分別為35 kg/(m2·s)和198 kg/h.董巖等[11,12]對于不同的截面形狀對換熱性能的影響也進行了研究,得出了換熱面積相同的情況下,U型截面的流道換熱效果優于其他截面形狀的流道.

基于靜止狀態多通道烘缸研究,王莎等[13,14]設計了多通道烘缸的旋轉實驗臺,并進行了應力分析和模態數值分析,確保了實驗臺的機械安全性,隨后又以該實驗臺為基礎,對旋轉狀態下多通道烘缸的換熱性能與壓降的研究[15,16],得出換熱系數隨雷諾數、旋轉雷諾數與入口蒸汽溫度的變化規律,以及壓降隨蒸汽質量流速,旋轉雷諾數的變化規律,并對旋轉狀態下的換熱系數和壓降給出了新的擬合公式,有較好的吻合度.張樹林等[17]對旋轉狀態下,冷卻水側的參數變化對烘缸換熱性能及壓降的影響進行了研究,指出通道平均換熱系數隨冷卻水質量流量的增大而增大,壓降則隨之減小并穩定于以定值.

由上可見,對于多通道烘缸換熱性能方面的研究已經較為成熟且豐富,對于烘缸換熱系數與各參數間的關系進行了深入研究并得出了適合的關系式,但所得關系式往往參考變量多,形式復雜,難以以直觀地方式明確得到換熱系數隨各參數的變化趨勢,從而難以對烘缸換熱性能進行可行的優化操作.

響應面分析法是通過設計合理的有限次數試驗,建立一個包括各顯著因素的一次項、平方項和任何兩個因素之間的一級交互作用項的數學模型,精確研究各因素與響應值之間的關系,快速有效地確定多因素系統的最佳條件.相比基于相似性原理的無量綱關系式,響應面分析法得出的多元二次多項式形式更為簡潔,可以更直接的把握各自變量與因變量的函數關系,更容易進行優化處理.為探究烘缸換熱性能的優化方向與具體的優化參數,本文選取轉速和蒸汽質量流速為代表變量,利用響應面分析法,對烘缸的換熱性能與二變量間的關系進行研究,并得出具體的參數優化區間.

1 實驗原理

實驗針對多通道烘缸中發生冷凝換熱的兩相部分進行研究.考慮到烘缸尺寸等參數的差異,要對換熱系數、蒸汽質量流速和轉速三個參量進行無量綱處理,同時考慮實驗過程中可能出現的熱損失,以保證結果的準確性和可推廣性.

(1)無量綱換熱系數,采用對流換熱常用的努塞爾數Nu為代表:

(1)

式(1)中:Dh為蒸汽側通道的水力直徑,m;λH為蒸汽側流體兩相熱導率,W·m-1·K-1:

(2)

式(2)中:λg,λl分別為當前溫度下飽和汽與飽和水的熱導率,W·m-1·K-1;x為當前流體的干度,即質量含汽率,其計算方法如下:

(3)

式(3)中:h′與h″分別為當前蒸汽側溫度下的飽和水比焓與飽和氣比焓,kJ·kg-1,均根據當前蒸汽側流體溫度查表獲得[18];h為當前蒸汽側流體的比焓,kJ·kg-1,由于流道中各位置的比焓根據能量守恒定律,因此可通過計算冷卻水側的吸熱量對其進行計算:

(4)

式(4)中:hi+1為目標位置的流體比焓,kJ·kg-1;hi為目標上一位置的比焓,kJ·kg-1;cp為冷卻水的定壓比熱容,kJ·kg-1·K-1;qm,c為冷卻水的質量流量,kg·s-1;Tc,i+1和Tc,i則是對應的冷卻水溫度,K.

式(1)中:hs為蒸汽側對流換熱系數,W·m-2·K-1,具體計算方式由牛頓對流換熱公式獲得:

(5)

式(5)中:As為換熱面積,m2;Ts為當前蒸汽側溫度,K;Tw為對應的換熱壁面溫度,K;Q為換熱熱量,kJ;根據能量守恒定律,在熱損失較小可忽略不計的情況下,蒸汽側放熱熱量等于冷卻水側吸熱量,即:

Qi=cpqm,c(Tc,i+1-Tc,i)

(6)

(2)無量綱流速,以流道中的氣相雷諾數Reg為代表:

(7)

式(6)中:G為流道內流體的質量流速,kg·m-2·s-1,為當前通道內流體質量流量qm,s,kg·s-1,與流道橫截面積A,m2,的比值:

(8)

式(8)中:μg、μl為流道內流體的氣相動力粘度(Pa·s),其具體值為當前溫度下的飽和水蒸氣動力粘度,由當前蒸汽側溫度查表獲得.

(3)無量綱轉速,以旋轉雷諾數Reω為代表,該無量綱參數由Morris提出并用于旋轉狀態下的換熱系數關系式計算[19,20],其計算公式如下:

(9)

式(9)中:ω為流道旋轉的角速度,rad·s-1;νH為流道的兩相運動粘度,m2·s-1,其計算公式如下:

(10)

式(10)中:νg和νl分別為當前溫度下飽和蒸汽與飽和水的運動粘度,m2·s-1,可根據當前蒸汽側溫度查表獲得.

(4)熱損失方面,考慮到熱損失過程接近于管外強迫對流換熱,因此基于管外強迫對流換熱公式[21]即可計算熱損失,具體公式如式(11)所示:

(11)

式(11)中:Nuloss為強迫對流換熱的努塞爾數;ha為熱損失的對流換熱系數,W·m-2·K-1;L為流道長度,m;λa為空氣熱導率,W·m-1·K-1;Rea和Pra分別為空氣的雷諾數與普朗特數,可以根據轉速和當前室溫溫進行查表.

2 實驗設計

根據理論部分,需要測量的物理量包括蒸汽側流體、冷卻水和換熱壁面的溫度、蒸汽側質量流量,同時設定實驗臺轉速.具體設計的實驗臺的結構如圖2所示.

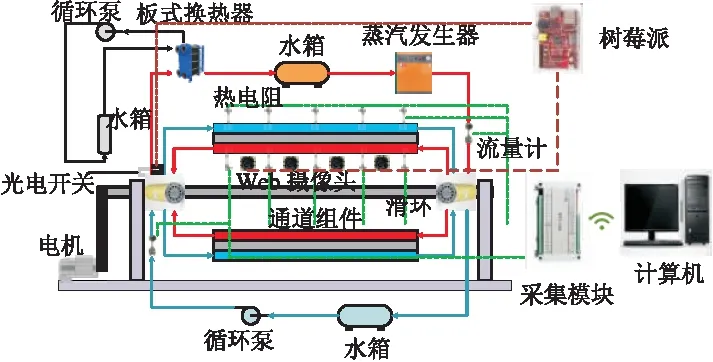
圖2 實驗臺結構示意圖

實驗臺由機械系統、流體循環系統和傳感器系統三大部分組成,機械系統包括最基礎的支撐結構部分旋轉電機,其中電機的轉速由相連的變頻器進行控制,并經過折算得到對應的轉動角速度.

流體循環系統包括蒸汽發生器、連接管路、分布滑環、流道板、換熱器、循環水泵、儲水箱、濾水系統等部分組成.蒸汽由蒸汽發生器產生,冷卻水由冷卻水泵泵出,經管道分別送至實驗臺兩側的分布滑環,分布滑環保證實驗臺在轉動情況下,蒸汽和冷卻水可以順利被送入送出流道板,蒸汽和冷卻水在流道板中進行熱交換后,由分別由各自對側的滑環流出,送入換熱器進行冷卻,蒸汽側冷凝水經過濾后流入發生器水箱,冷卻水側冷水則進入冷卻水箱,分別進入下一次的循環.流道板除了正反兩側的蒸汽/冷卻水流道外,流道周圍有凹槽安裝隔熱的密封條,如圖3所示;同時整個流道板和蒸汽側進口段管路均有厚度在1～3 cm的隔熱棉包裹,最大限度的減少熱損失.經計算,實驗臺的熱損失小于2%,可以忽略不計.最終搭建完畢的實驗臺如圖4所示.

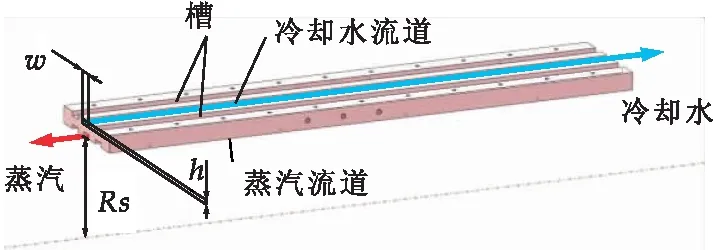
圖3 流道板結構示意圖

圖4 實驗臺實物圖

本實驗所用傳感器系統是采集各種參數數據的部分,主要包括PT100熱電阻、流量計、信號采集卡三部分,熱電阻的排布如圖5所示,分布于整個流道板上,共分為三組,分別測量蒸汽側流體、冷卻水側流體和兩側中間的換熱壁面的溫度.蒸汽側和冷卻水側的流道入口均設有流量計測量兩回路的流量.熱電阻的信號則由采集卡采集,并通過Wi-Fi傳輸至計算機.

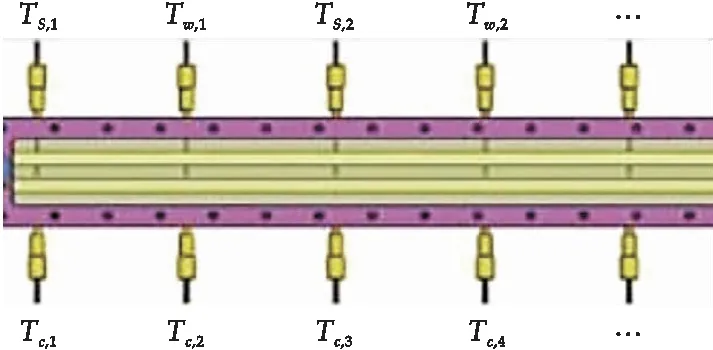
圖5 熱電阻排布示意圖

本實驗臺所使用的傳感器精度如表1所示,實驗臺的結構尺寸參數如表2所示,實驗的具體參數如表3所示.具體的實驗步驟如下:

表1 傳感器精度表

表2 實驗臺結構參數

表3 實驗參數表

(1)接通所有用電設備電源,蒸汽發生器預熱,連接所有無線傳輸模塊,測試各傳感器讀數是否正常.

(2)打開所有管路,調整冷卻水流量;調整蒸汽發生器溫度至設定值,微調流量控制閥至蒸汽質量流量達到實驗所需大小.

(3)啟動電機,通過變頻器控制當前轉速,待傳感器讀數基本穩定后開始采集數據.

(4)數據采集完成后,調整電機轉速或蒸汽流量,繼續下一組數據的采集,直至所有實驗組數據采集完畢.

(5)斷開所有用電器電路,確認電源總閘關閉;蒸汽發生器帶壓排污,關閉進水口,排空進水水箱;保持冷卻水持續供應至實驗臺完全冷卻,關閉所有管路.

(6)所采集的數據經Excel預處理后,交予Python做進一步處理,繪圖,得出所需方程.

3 實驗結果與優化分析

3.1 實驗結果

實驗結果以Reg和Reω為坐標的三維散點圖展示如圖6所示.由圖6可知,提高蒸汽質量流速對換熱性能有整體上的提升,而在兩較高的質量流速下,隨著轉速增大,換熱性能亦隨之提升,但在流速較低時,Nu基本只隨Reω變化而出現小幅波動,而沒有大的明顯變化,可見流速較低時,轉速對換熱性能的影響是相對有限的.由于本實驗只針對出現冷凝換熱的部分進行研究分析,沒有冷段的溫度數據參與計算,因此本實驗所得的Nu整體上要大于文獻[15]中所得的結果,但所得變化規律基本與文獻[15]中所描述的一致.

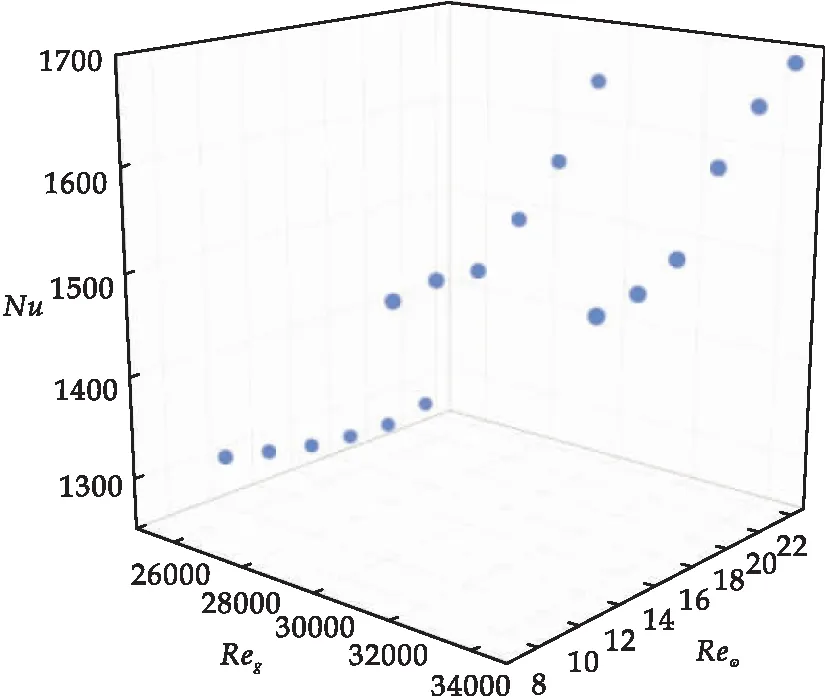
圖6 Nu隨Reg和Reω變化的三維分布圖

圖6較好地表現了實驗所得的換熱性能的變化情況,但要總結換熱性能隨轉速和蒸汽質量流速的變化規律,優化對還需要對數據進行進一步的處理與分析.

3.2 響應面的構建

圖6展示的實驗結果表明,因變量Nu與自變量Reg和Reω并非二維線性關系,因此構建響應面的擬合函數采用二次多項式,如公式(12)所示:

(12)

式(12)中:bi為擬合系數,ε為誤差.視所有一次項和二次項均為不同的一次自變量,則可將該二元二次多項式化為多元線性多項式:

(13)

式(13)中:xi為公式12中對應的各一次項與二次項變量.由于Reg與Reω以及相關二次項變量的數量級相差過大,因此為保證結果的精度,降低擬合誤差,對各自變量采用標準化處理,即:

(14)

式(14)中:μi、σi分別為xi訓練值的均值與標準差.最終線性回歸方程為:

(15)

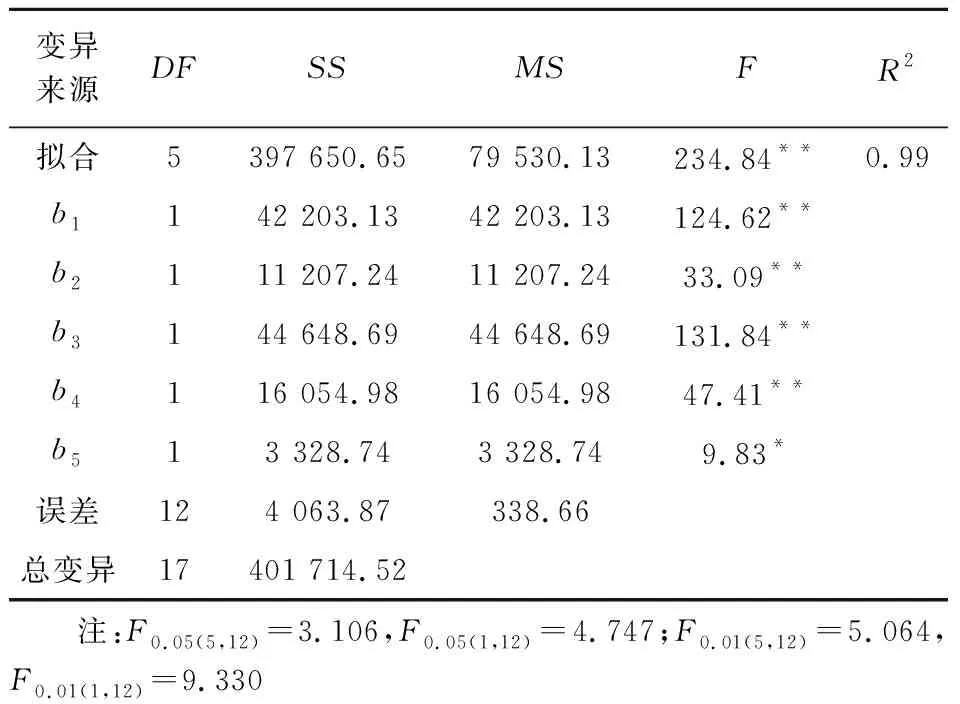
表4 回歸方程的方差分析

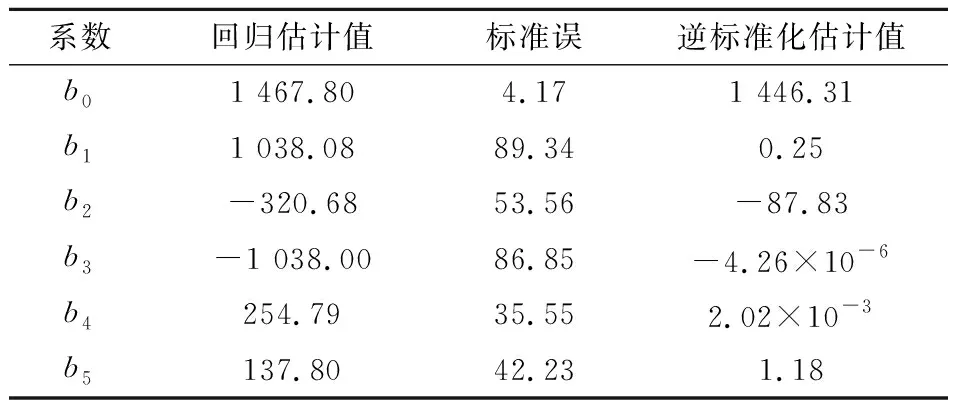
表5 回歸系數的估計值與標準誤

由此可列出回歸方程為:

(16)

或:

(17)

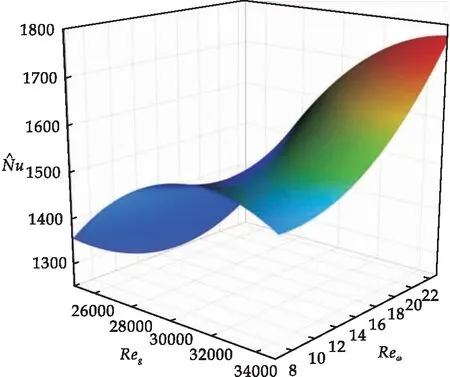
圖7 對Reg和Reω的響應面

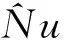
3.3 基于響應面的優化分析

為了對Reg和Reω進行優化分析,令式(17)分別對Reg和Reω取一階偏導,可以得到:

(18)

令式(18)兩式分別等于零并聯立求解,我們可以得到駐點,但函數在駐點處的Hessian矩陣為不定矩陣,因此該駐點為鞍點而非極值點,方程在該區間內最大值即為Reg和Reω均取最大時的值.由此可見,在當前實驗區間內,保證盡可能高的質量流速和轉速是獲得高換熱性能的必要條件.

Reg*=237.09Reω,c+2.93×104

(19)

(20)

式(19)、(20)中:Reg*與Reω*分別表示兩變量的最優值;Reg,c與Reω,c分別表示兩變量取區間內定值.

3.3.1 定Reω下的參數優化分析

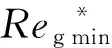
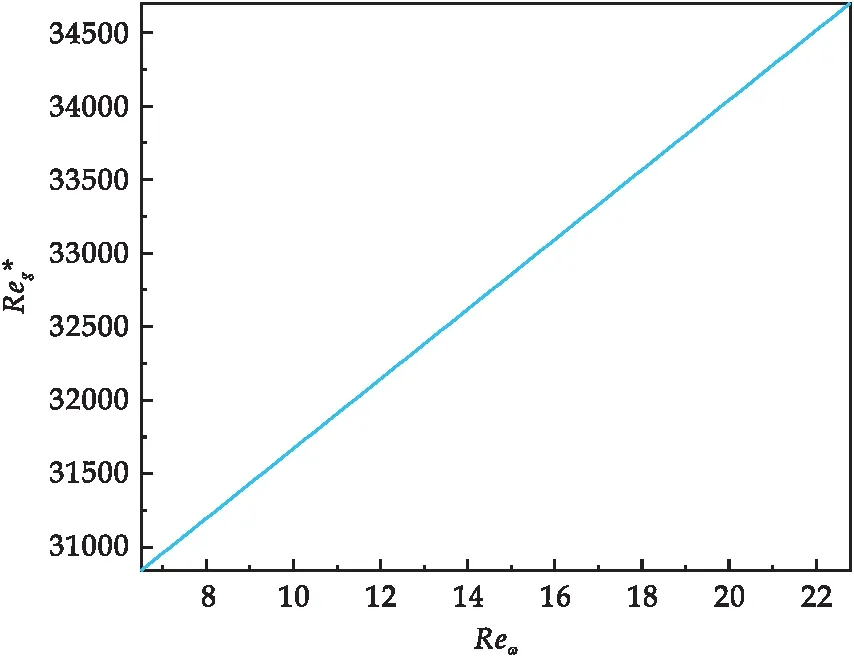
圖8 Reg*關于Reω的函數圖像

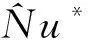
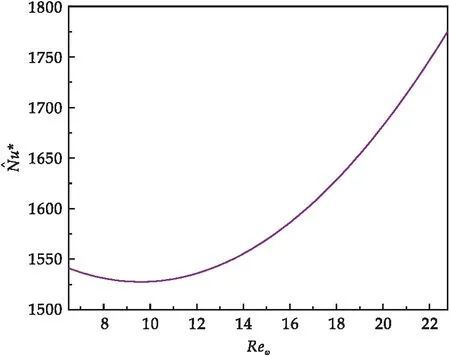
圖9 關于Reω的函數圖像

3.3.2 定Reg下的參數優化分析

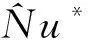
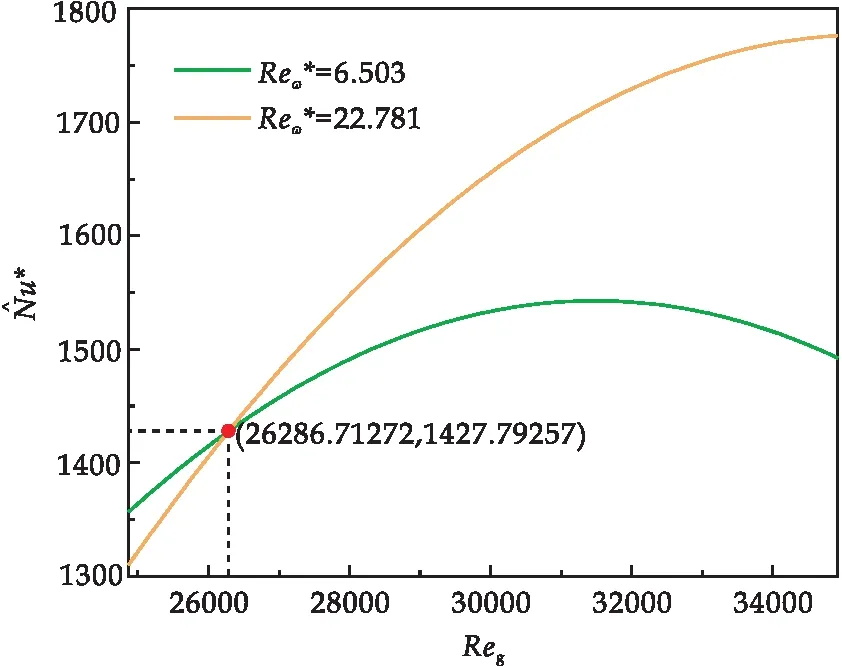
圖10 不同Reω*條件下關于Reg函數圖像

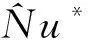
(21)

3.3.3 當前區間的綜合優化分析

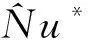
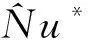
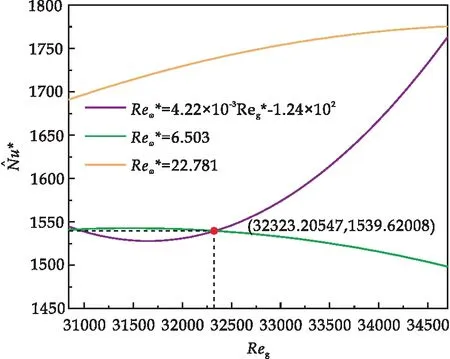
圖11 不同優化方案的對比

根據以上分析,可以得出當前區間內多通道烘缸換熱系數的最終的優化結果.當轉速一定而蒸汽質量流速可調時,質量流速應至少保證氣相雷諾數Reg不小于30 841.80;若質量流速不能保證Reg大于32 323.21,則相比維持當前所能達到的轉速,保持較低的轉速能獲得更好的換熱效果;在能夠保證Reg大于32 323.21的情況下,維持Reg的取值滿足式(19)的條件可獲得最大的換熱系數.

當蒸汽質量流速一定而轉速可調時,若質量流速對應的Reg小于26 286.71,保持區間內最低轉速可以獲得最佳換熱效果;當Reg大于26 286.71時,保持區間內最高轉速可令換熱系數達到最大.當轉速與蒸汽質量流速均可在當前區間內調整,則同時保持區間內最大的轉速和質量流速方可獲得區間內的最優換熱系數.

然而對于實際生產,除了考慮以上因素外,還要考慮工藝、能耗、設備損耗等因素,以獲得最符合實際情況的最優換熱系數.

4 結論

綜上所述,可得出如下結論:

(1)蒸汽的質量流速較低時,轉速對于換熱性能的提升影響很小;而在高蒸汽質量流速下,轉速對于換熱性能的提升影響要大于蒸汽質量流速的影響,蒸汽質量流速的增大只有在轉速達到一定值的情況下才有意義.

(2)當轉速一定時,質量流速應至少保證氣相雷諾數Reg不小于30 841.80;當質量流速不能保證Reg大于32 323.21時,轉速應當降低;在能夠保證Reg大于32 323.21的情況下,維持Reg的取值滿足對應的線性關系,這樣可獲得最優的換熱系數.

(3)當蒸汽質量流速一定時,若質量流速對應的Reg小于26 286.71,保持區間內最低轉速可以獲得最佳換熱效果;當Reg大于26 286.71時,保持區間內最高轉速可令換熱系數達到最大.

(4)烘缸的實際蒸汽質量流速與轉速應為獲得盡可能高的換熱性能服務,但也應在考慮實際工況與成本問題后,做出最優方案.