基于融合嵌入向量的多目標優(yōu)化社區(qū)發(fā)現(xiàn)
韓存鴿, 陳展鴻, 郭 昆*
(1.武夷學(xué)院 數(shù)學(xué)與計算機學(xué)院 福建省茶產(chǎn)業(yè)大數(shù)據(jù)應(yīng)用與智能化重點實驗室, 福建 武夷山 354300; 2.福州大學(xué) 計算機與大數(shù)據(jù)學(xué)院, 福建 福州 350108)
0 引言
現(xiàn)實世界中的許多復(fù)雜系統(tǒng)都可以建模為網(wǎng)絡(luò),如生物網(wǎng)絡(luò)、社交網(wǎng)絡(luò)、科學(xué)合作網(wǎng)絡(luò)等.在這些網(wǎng)絡(luò)中,節(jié)點之間的連接關(guān)系非常復(fù)雜,節(jié)點的度、聚集系數(shù)、連通性等屬性也各不相同.社區(qū)發(fā)現(xiàn)[1]是復(fù)雜網(wǎng)絡(luò)研究中的一個重要領(lǐng)域,其主要目的是發(fā)現(xiàn)網(wǎng)絡(luò)中的社區(qū)結(jié)構(gòu).社區(qū)發(fā)現(xiàn)可以從節(jié)點屬性角度進行分類,分為無屬性網(wǎng)絡(luò)和屬性網(wǎng)絡(luò)的社區(qū)發(fā)現(xiàn).在過去,許多社區(qū)發(fā)現(xiàn)算法僅考慮網(wǎng)絡(luò)結(jié)構(gòu),忽略了節(jié)點間的屬性信息.然而,現(xiàn)實世界中許多網(wǎng)絡(luò)都具有屬性,如社交網(wǎng)絡(luò)中的個人資料信息、科學(xué)合作網(wǎng)絡(luò)中的學(xué)科領(lǐng)域等.
基于進化計算的社區(qū)發(fā)現(xiàn)早期應(yīng)用于無屬性網(wǎng)絡(luò).2008年,Pizzuti[2]首次提出了GA-Net,該算法采用鄰位編碼的遺傳算法搜索社區(qū),是最早的基于進化的社區(qū)發(fā)現(xiàn)方法.隨后,一些基于多目標優(yōu)化的進化算法被應(yīng)用于社區(qū)發(fā)現(xiàn).2009年,Pizzuti[3]提出了基于多目標優(yōu)化的進化計算社區(qū)發(fā)現(xiàn)算法MOGA-Net,算法通過優(yōu)化社區(qū)得分和社區(qū)適應(yīng)度來完成無屬性網(wǎng)絡(luò)上的社區(qū)發(fā)現(xiàn).2013年,Gong等[4]提出的MODPSO結(jié)合粒子群算法,對核k均值(KKM)和比率割(RC)這兩個目標進行優(yōu)化,提高了社區(qū)發(fā)現(xiàn)的精度.2018年,Zhang等[5]提出了一種在大規(guī)模圖上進化計算進行社區(qū)發(fā)現(xiàn)的算法RMOEA,采用了一種節(jié)點規(guī)約策略來將同社區(qū)的節(jié)點合并成一個超級節(jié)點進行迭代,提高了算法的收斂速度與精度.此后,一些基于屬性網(wǎng)絡(luò)的社區(qū)發(fā)現(xiàn)算法被相繼提出.2017年,Li等[6]提出了MOEA-SA的多目標優(yōu)化社區(qū)檢測算法,通過優(yōu)化模塊度和屬性相似性來進行社區(qū)發(fā)現(xiàn),使得社區(qū)內(nèi)的節(jié)點間的邊密集并且屬性相似,提高了社區(qū)劃分的正確性.2019年,Pizzuti等[7]提出了MOGA-@Net算法,它嘗試對多種目標函數(shù)進行優(yōu)化,并通過合并社區(qū)的方式來提高社區(qū)發(fā)現(xiàn)的精度.2021年,Sun等[8]提出了CE-MOEA,其利用圖神經(jīng)網(wǎng)絡(luò)對網(wǎng)絡(luò)的邊進行編碼,每條邊都對應(yīng)著一個連續(xù)變量,最后通過邊的非線性變換來生成社區(qū)劃分.
目前,基于屬性網(wǎng)絡(luò)多目標優(yōu)化進化社區(qū)發(fā)現(xiàn)算法(MOEAs)主要面臨兩個挑戰(zhàn):(1)編碼方式都直接或間接使用鄰接編碼策略,使得算法的搜索能力易受網(wǎng)絡(luò)結(jié)構(gòu)限制,社區(qū)劃分的質(zhì)量不高;(2)進化算法容易陷入局部最優(yōu),導(dǎo)致社區(qū)發(fā)現(xiàn)的精度不高.
針對以上問題,本文提出一種基于融合嵌入向量的多目標優(yōu)化社區(qū)發(fā)現(xiàn)算法FEV-MOEA(Fusion Embedding Vector MOEA),首先,設(shè)計一種基于融合系數(shù)的編解碼方案,通過利用每個節(jié)點的屬性與結(jié)構(gòu)嵌入向量,以克服算法對網(wǎng)絡(luò)結(jié)構(gòu)的限制,提高社區(qū)劃分質(zhì)量.其次,提出一種后處理節(jié)點修正策略,通過該策略對社區(qū)劃分結(jié)果進行修正,提高社區(qū)劃分的精度.主要創(chuàng)新點如下:
(1)通過設(shè)計融合系數(shù)編解碼方案,充分利用節(jié)點屬性、結(jié)構(gòu)嵌入向量.編碼時,采用連續(xù)值編碼方式,將每個節(jié)點編碼成一個基因位,每個基因值表示該節(jié)點結(jié)構(gòu)、屬性嵌入向量的融合程度,避免了傳統(tǒng)編碼方案中丟失節(jié)點間連續(xù)信息的問題.解碼時,根據(jù)融合嵌入向量結(jié)合聚類算法,使得解碼方式不受網(wǎng)絡(luò)結(jié)構(gòu)的限制,以提升社區(qū)發(fā)現(xiàn)的質(zhì)量.
(2)通過設(shè)計后處理節(jié)點修正策略,不斷優(yōu)化新社區(qū)的模塊度與社區(qū)內(nèi)屬性相似度,使得算法的解能夠克服陷入局部最優(yōu)的問題,提高社區(qū)發(fā)現(xiàn)的精度.
(3)通過在真實和人工數(shù)據(jù)集上實驗,驗證了FEV-MOEA算法能夠有效提高社區(qū)發(fā)現(xiàn)的精度.
1 FEV-MOEA算法
1.1 基本概念
定義1復(fù)雜網(wǎng)絡(luò):復(fù)雜網(wǎng)絡(luò)可以被建模三元組G=(V,E,A),其中V={v1,v2,…,vn}表示節(jié)點集合,n代表網(wǎng)絡(luò)節(jié)點數(shù).E={(vi,vj)|vi,vj∈V,i≠j},表示網(wǎng)絡(luò)邊的集合,A=[a1,a2,…,an]T∈R|v|×m表示節(jié)點的屬性矩陣.
定義2節(jié)點嵌入向量:節(jié)點嵌入向量是指將網(wǎng)絡(luò)中的每個節(jié)點表示為一個低維的實數(shù)向量,它們可以將節(jié)點間的拓撲與屬性結(jié)構(gòu)信息轉(zhuǎn)換為低維向量空間中的向量,從而可以在向量空間中進行節(jié)點的聚類操作.
定義3模塊度Q:模塊度Q是復(fù)雜網(wǎng)絡(luò)中用于衡量社區(qū)結(jié)構(gòu)的一種指標,通常用符號Q表示.它衡量了某種分割方式下,網(wǎng)絡(luò)中的節(jié)點分配到社區(qū)的緊密程度與該分割方式隨機下產(chǎn)生的網(wǎng)絡(luò)中的節(jié)點分配到社區(qū)的緊密程度之差.
(1)
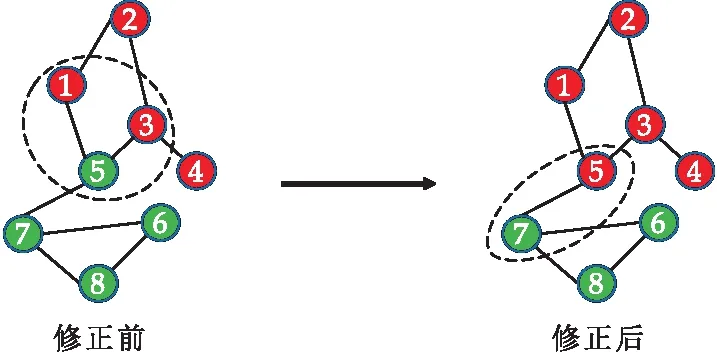
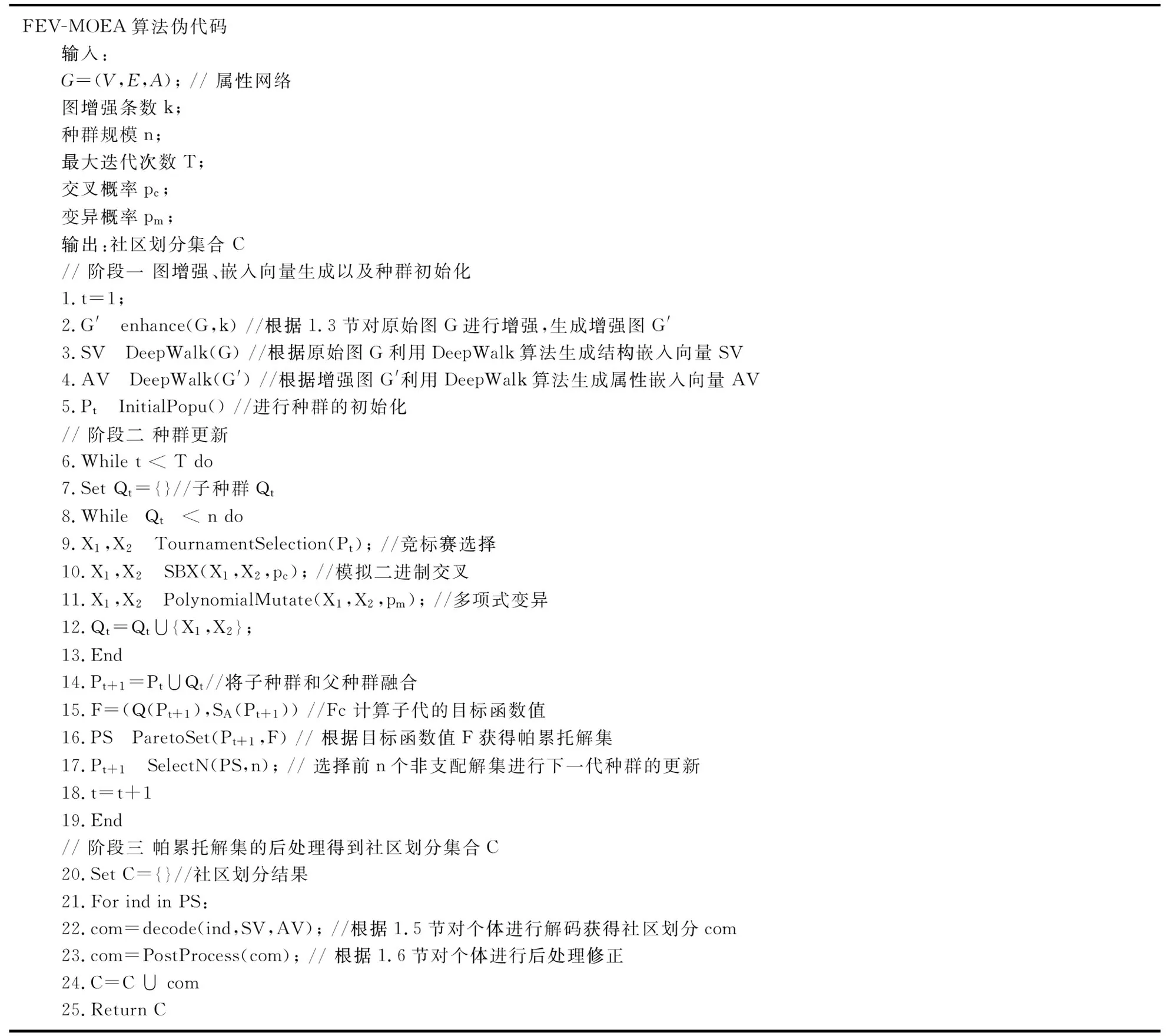
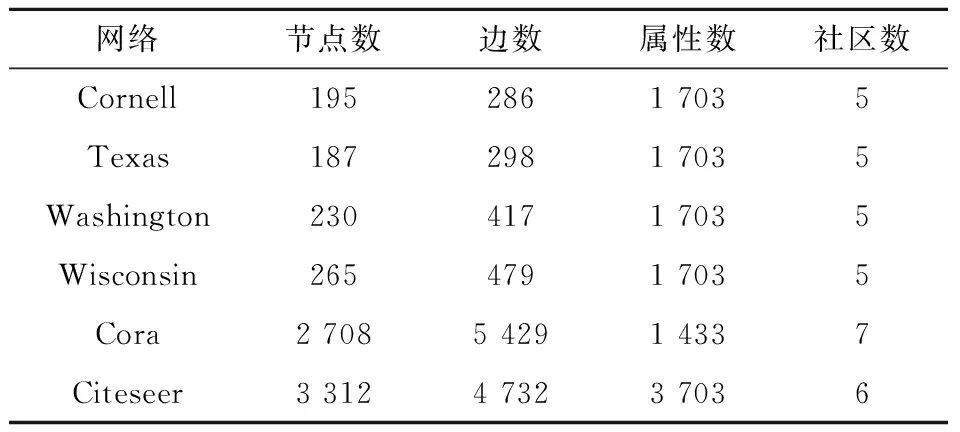
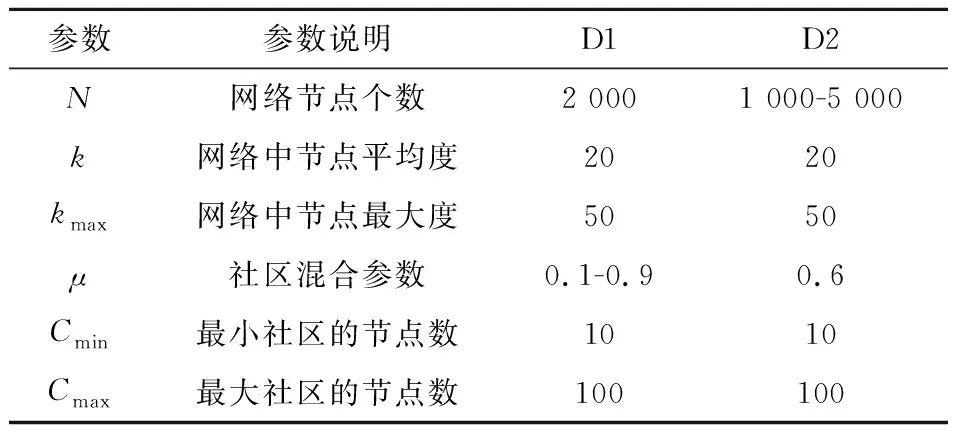
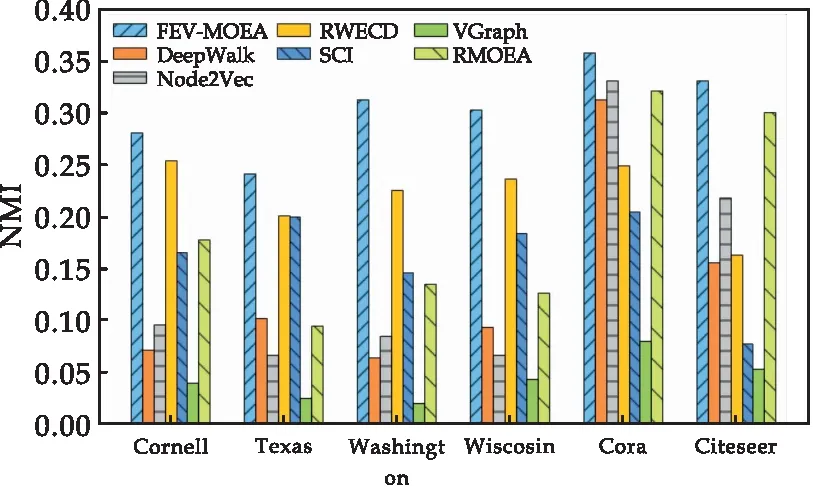
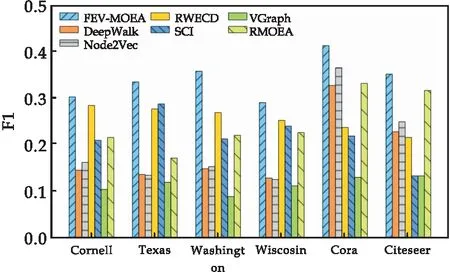
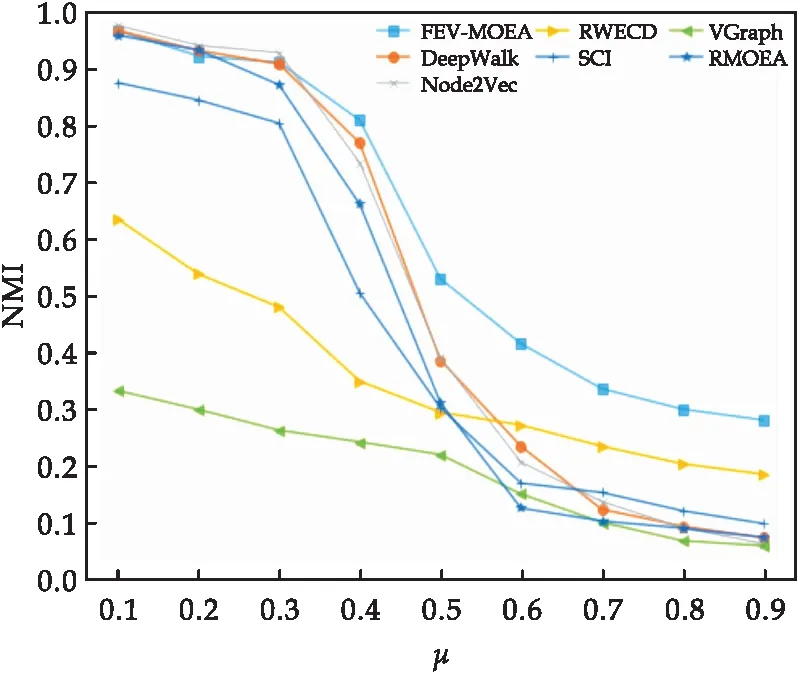
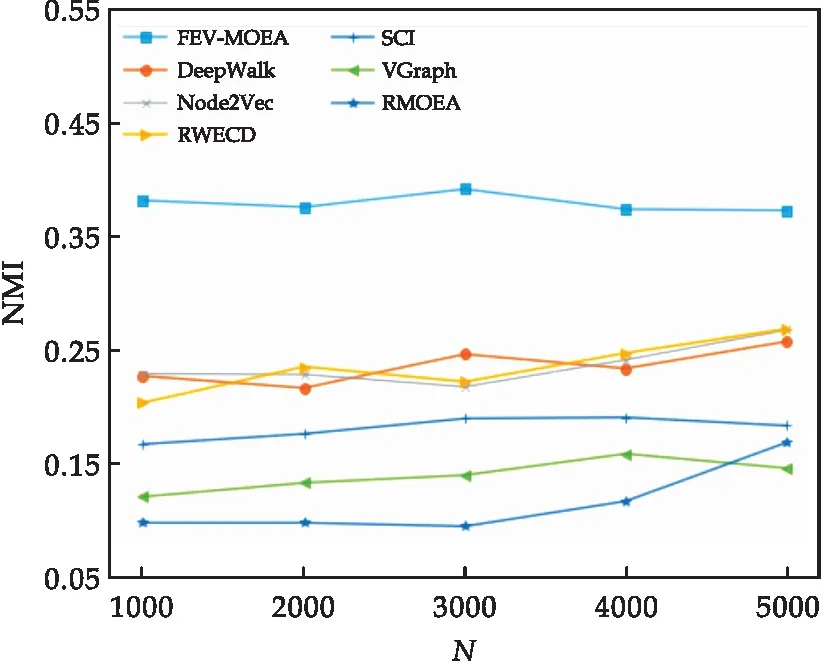
式(1)中:1= 定義4節(jié)點屬性相似度s(i,j):節(jié)點屬性相似度用來刻畫兩個節(jié)點關(guān)于屬性上的相似情況,兩個節(jié)點越相似,則兩節(jié)點的屬性相似度越高. s(i,j)定義為: (2) 定義5社區(qū)內(nèi)屬性相似度SA.社區(qū)內(nèi)屬性相似度SA是社區(qū)發(fā)現(xiàn)中用于衡量在屬性上劃分社區(qū)的質(zhì)量.當(dāng)同一個社區(qū)內(nèi)的節(jié)點屬性越相似,則社區(qū)內(nèi)屬性相似度SA越高. (3) 式(3)中:c是劃分社區(qū)的總數(shù),ck表示第k個社區(qū)的節(jié)點集合,s(i,j)定義節(jié)點間的屬性相似度,rk為第k個社區(qū)的節(jié)點個數(shù). 多目標優(yōu)化:多目標優(yōu)化研究如何在具有多個目標的優(yōu)化問題中找到一組最優(yōu)解.在傳統(tǒng)的單目標優(yōu)化問題中,目標函數(shù)單一,優(yōu)化目標是最小化或最大化一個特定的目標.而在多目標優(yōu)化問題中,存在多個目標函數(shù),無法簡單地將它們歸納為單一目標函數(shù).在多目標優(yōu)化理論中,存在解支配關(guān)系.在兩解x,y中,如果x在所有目標上優(yōu)于y,則稱解x支配解y,x為非支配解.支配關(guān)系表示解之間的優(yōu)劣關(guān)系.而帕累托解集是一組非支配解的集合,表示了多目標優(yōu)化問題的最優(yōu)解的信息,多目標優(yōu)化算法旨在搜索并逼近帕累托解集.在基于多目標的屬性網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)中,研究重點在于如何利用蘊含在節(jié)點中的屬性信息以及節(jié)點間的結(jié)構(gòu)關(guān)系,去檢測潛在的社區(qū):(1)在結(jié)構(gòu)上,檢測出的社區(qū)內(nèi)部節(jié)點的邊較為密集,而社區(qū)間節(jié)點的邊較為稀疏;(2)在屬性上,同一個社區(qū)內(nèi)部的節(jié)點屬性相似度較高.因此基于多目標優(yōu)化的屬性網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)問題可以建模為:min{Q,SA}. FEV-MOEA 的算法框架如圖1所示,由三個階段構(gòu)成,分別為圖增強、嵌入向量生成以及個體初始化階段、種群與帕累托前沿的更新階段、以及后處理修正階段.在階段一中,首先,將原始圖根據(jù)屬性信息構(gòu)造增強圖,使得圖上的屬性信息更加豐富.接著,利用DeepWalk分別獲得結(jié)構(gòu)、屬性上的嵌入向量.最后,根據(jù)嵌入向量初始化個體.階段二將個體進行交叉、變異與選擇操作來更新種群在解空間搜尋優(yōu)秀個體.階段三將帕累托解集進行后處理修正,使得可行解能夠避免陷入局部最優(yōu)的問題. 圖1 FEV-MOEA算法框架 1.3.1 圖增強 圖2表示k=2時,節(jié)點5的圖增強示意圖. 圖2 圖增強示意圖 在屬性網(wǎng)絡(luò)中,存在著一類結(jié)構(gòu)與屬性信息不一致的社區(qū),即在社區(qū)內(nèi)的節(jié)點在結(jié)構(gòu)上并沒有明顯的社區(qū)邊界,甚至出現(xiàn)隸屬于同一個社區(qū)的節(jié)點在不同的連通分支,但它們的屬性相類似.這種結(jié)構(gòu)與屬性信息不一致的網(wǎng)絡(luò)會導(dǎo)致算法精度降低,為了更好地識別節(jié)點之間的潛在關(guān)系,需要根據(jù)節(jié)點間的屬性對原始圖結(jié)構(gòu)進行增強,通過增強的圖結(jié)構(gòu),可以更準確地識別節(jié)點之間的社區(qū),從而更好地理解復(fù)雜系統(tǒng)中節(jié)點之間的相互作用.具體圖增強策略如下:對于每個節(jié)點V,計算出前k個與其節(jié)點屬性相似度最大的節(jié)點集合,將V與節(jié)點集合里的每個節(jié)點新增一條邊完成圖增強. 1.3.2 嵌入向量生成 FEV-MOEA解碼時需要結(jié)合結(jié)構(gòu)、屬性嵌入向量得到最終的社區(qū)劃分,因此需要生成對應(yīng)的結(jié)構(gòu)、屬性嵌入向量用于后續(xù)個體的解碼.FEV-MOEA采用DeepWalk[9]算法分別生成結(jié)構(gòu)、屬性嵌入向量.DeepWalk是一種基于隨機游走的網(wǎng)絡(luò)嵌入方法,用于將節(jié)點映射到低維向量空間中,它通過捕捉節(jié)點在網(wǎng)絡(luò)中的局部鄰域來捕捉節(jié)點的相似性,并將其表示為低維向量,DeepWalk由隨機游走與Skip-gram模型兩個關(guān)鍵步驟組成,隨機游走生成了大量的遍歷序列,而Skip-gram模型將這些序列看作自然語言中的句子,并通過最大化預(yù)測周圍節(jié)點出現(xiàn)概率的目標函數(shù)來學(xué)習(xí)節(jié)點向量表示.圖3展示了結(jié)構(gòu)嵌入向量與屬性嵌入向量的生成例子.針對結(jié)構(gòu)嵌入向量初始化,游走序列采取原始圖上的隨機游走,而針對屬性嵌入向量初始化,游走序列采取增強圖上的隨機游走. 圖3 結(jié)合DeepWalk生成嵌入向量 1.3.3 種群初始化 在進化計算的社區(qū)發(fā)現(xiàn)算法中,傳統(tǒng)的編碼方案分基于節(jié)點標簽的編碼方案(Label-based)與基于鄰居節(jié)點的編碼方案(Locus-based)兩種.Label-based編碼將每個節(jié)點編碼成一個基因位,每個基因位的值表示節(jié)點所屬的社區(qū),解碼時每個基因的值就代表著該節(jié)點隸屬的社區(qū).該編碼方案需要將編碼進行離散化編碼,會丟失節(jié)點之間的連續(xù)性信息,可能會導(dǎo)致進化失去部分信息. 而Locus-based是將每個節(jié)點編碼成一個基因位,每個基因位的值標識該節(jié)點的某個鄰居節(jié)點的編號,解碼時將該節(jié)點與其基因值對應(yīng)的鄰居節(jié)點劃分為同一個社區(qū).現(xiàn)有編碼方案難以克服局部最優(yōu),比如,若一個節(jié)點在進化過程中被分配到一個錯誤的標簽時,其周圍的節(jié)點也可能被分配到相同的錯誤標簽,可能會導(dǎo)致算法陷入局部最優(yōu),同時因受到網(wǎng)絡(luò)結(jié)構(gòu)的影響,劃分社區(qū)的節(jié)點必須在同一個連通分支. 在FEV-MOEA中,設(shè)計一個基于融合系數(shù)的編碼及解碼方案,圖4為基于融合系數(shù)的編碼示意圖.如圖4所示,增強圖共有8個節(jié)點,編碼時將每個節(jié)點編碼成一個基因位,每個基因值代表著該節(jié)點關(guān)于結(jié)構(gòu)、屬性嵌入向量的融合程度,具體基因值的初始化詳見InitialPopu偽代碼.圖5為基于融合系數(shù)的解碼示意圖,其中,gen(i)表示i節(jié)點對應(yīng)的融合系數(shù),Si表示i節(jié)點的結(jié)構(gòu)嵌入向量,Ai表示i節(jié)點的屬性嵌入向量.結(jié)合Si與Ai,可以通過公式gen(i)*Si+(1-gen(i))*Ai計算加權(quán)后節(jié)點i的融合嵌入向量Fi.當(dāng)節(jié)點1的結(jié)構(gòu)嵌入向量S1為[40,50],屬性嵌入向量A1為[80,60]時,則融合嵌入向量F1=0.63*[40,50]+0.37*[80,60]=[55,54].計算所有節(jié)點的融合嵌入向量F后,結(jié)合Kmeans[10]聚類算法得到最終的社區(qū)劃分. 圖4 基于融合系數(shù)的編碼方案 圖5 基于融合系數(shù)的解碼示例 種群初始化后需要經(jīng)過多次選擇、交叉與變異算子使得種群逼近全局最優(yōu)解.為了適配提出的基于融合系數(shù)的編碼方案,本文的選擇算子為錦標賽選擇算子,錦標賽選擇算子是一種常用的選擇算子,其思想是隨機選擇一定數(shù)量的個體作為競爭者,從中隨機選擇若干個非支配解,作為下一代的子種群的父代.而交叉算子采取模擬二進制交叉,模擬二進制交叉是一種常用的交叉算子,其主要過程是先選擇倆個父代個體,再對于每對等位基因確定其交叉概率和分布指數(shù),計算最終交叉的中間變量得到子代交叉后的基因值.而變異算子采用多項式變異,多項式變異可以用于連續(xù)值編碼的變異操作,增加搜索空間的探索能力,其主要思想是對于每一個基因,計算其變異區(qū)間,再根據(jù)變異區(qū)間的范圍對基因值進行變異操作,變異區(qū)間的大小會受到變異概率的影響.父種群經(jīng)過多次的選擇、交叉與變異操作后得到子種群,接著通過父、子種群的目標函數(shù)值選出帕累托解集,從帕累托解集中選擇若干個個體參與下輪種群的更新迭代,直至迭代次數(shù)達到最大次數(shù). 復(fù)雜網(wǎng)絡(luò)結(jié)構(gòu)與屬性的復(fù)雜性和規(guī)模會影響算法的效果,當(dāng)社交網(wǎng)絡(luò)結(jié)構(gòu)較為復(fù)雜時,算法容易出現(xiàn)局部最優(yōu)解.為避免算法陷入局部最優(yōu),提出一種基于目標函數(shù)最優(yōu)的節(jié)點修正策略,策略將帕累托解集中的邊緣節(jié)點所屬社區(qū)進行修正,使得修正后的社區(qū)劃分結(jié)果具有更高的模塊度Q與社區(qū)內(nèi)屬性相似度SA,以克服局部最優(yōu)的問題,提高社區(qū)劃分的精度. 在后處理節(jié)點修正方案中,首先,計算出社區(qū)劃分的目標函數(shù)模塊度Q1與社區(qū)內(nèi)屬性相似度SA1.其次,找到與其他社區(qū)有連接邊的節(jié)點, 稱之為邊緣節(jié)點.接著,將這些邊緣節(jié)點嘗試加入到相鄰社區(qū),重新計算目標函數(shù)模塊度Q2與社區(qū)內(nèi)屬性相似度SA2.最后,當(dāng)Q2>Q1且SA2>SA1時,則將這些邊緣節(jié)點加入到相鄰社區(qū),否則不加入.圖6為后處理修正的例子,其中修正前節(jié)點1、3、5為邊緣節(jié)點,當(dāng)邊緣節(jié)點1和3嘗試加入到相鄰社區(qū)時,模塊度Q與社區(qū)內(nèi)屬性相似度SA并不會提高,因此邊緣節(jié)點1和3的社區(qū)標簽并不進行修正,而邊緣節(jié)點5嘗試加入到相鄰社區(qū)時,模塊度Q與社區(qū)內(nèi)屬性相似度SA都會提高,因此將邊緣節(jié)點5加入到鄰近社區(qū),社區(qū)標簽進行修正.修正后,邊緣節(jié)點為5、7,而節(jié)點5、7嘗試加入到鄰近社區(qū)都不會使模塊度Q與社區(qū)內(nèi)屬性相似度SA提高,后處理修正結(jié)束. 圖6 后處理修正 FEV-MOEA算法基于NSGA-II進化框架進行實現(xiàn).(Non-dominated Sorting Genetic Algorithm II,NSGA-II):NSGA-II是一種常用的多目標進化計算方法,它是基于遺傳算法的一種擴展,能夠同時優(yōu)化多個目標函數(shù).以下是FEV-MOEA的算法偽代碼: FEV-MOEA算法偽代碼輸入:G=(V,E,A); // 屬性網(wǎng)絡(luò)圖增強條數(shù)k;種群規(guī)模n;最大迭代次數(shù)T;交叉概率pc;變異概率pm;輸出:社區(qū)劃分集合 C// 階段一 圖增強、嵌入向量生成以及種群初始化1.t=1;2.G'←enhance(G,k) //根據(jù)1.3節(jié)對原始圖G進行增強,生成增強圖G'3.SV←DeepWalk(G) //根據(jù)原始圖G利用DeepWalk算法生成結(jié)構(gòu)嵌入向量SV4.AV←DeepWalk(G') //根據(jù)增強圖G'利用DeepWalk算法生成屬性嵌入向量AV5.Pt←InitialPopu() //進行種群的初始化// 階段二 種群更新6.While t < T do7.Set Qt={}//子種群Qt8.While |Qt| < n do9.X1,X2←TournamentSelection(Pt); //競標賽選擇10.X1,X2←SBX(X1,X2,pc); //模擬二進制交叉11.X1,X2←PolynomialMutate(X1,X2,pm); //多項式變異12.Qt=Qt∪{X1,X2};13.End 14.Pt+1=Pt∪Qt //將子種群和父種群融合15.F=(Q(Pt+1),SA(Pt+1)) //Fc 計算子代的目標函數(shù)值16.PS←ParetoSet(Pt+1,F) // 根據(jù)目標函數(shù)值F獲得帕累托解集17.Pt+1←SelectN(PS,n); // 選擇前n個非支配解集進行下一代種群的更新18.t=t+119.End // 階段三 帕累托解集的后處理得到社區(qū)劃分集合C20.Set C={}//社區(qū)劃分結(jié)果 21.For ind in PS:22.com=decode(ind,SV,AV); //根據(jù)1.5節(jié)對個體進行解碼獲得社區(qū)劃分com23.com=PostProcess(com); // 根據(jù)1.6節(jié)對個體進行后處理修正24.C=C ∪ com25.Return C enhance( )函數(shù)對原始圖進行增強,偽代碼如下: enhance()函數(shù)偽代碼輸入:G=(V,E,A); // 屬性網(wǎng)絡(luò)原始圖,圖增強條數(shù) k;輸出:增強圖G' 1. G'=G 2. For i=1 to |N| do:3. sim=[] //節(jié)點i的屬性相似度列表4. For j=1 to |N| do:5. sim .add(s(i,j) ) // 節(jié)點屬性相似度s(i,j)6. similar_nodes=sort(sim) //根據(jù)屬性相似度降序排序,得到對應(yīng)的節(jié)點列表7. For n in similar_nodes:8. G'.addEdge(i,n) //添加一條從節(jié)點i到相似節(jié)點n的邊 Return G' InitialPopu( )函數(shù)用于種群初始化,其偽代碼為: InitialPopu算法偽代碼輸入:G=(V,E,A); // 屬性網(wǎng)絡(luò),種群規(guī)模 n;輸出:P //初始種群1.P={}2.For k=1 to n do:3. For i=1 to |N| do:4. Xk(gen(i))=1-s(i,j) //第k個個體節(jié)點i的融合系數(shù) 5. P←Xk6.Return P 為了驗證FEV-MOEA算法的性能,本文選擇6個對比算法在真實數(shù)據(jù)集與人工數(shù)據(jù)集進行實驗.其中,DeepWalk與Node2Vec[11]是基于隨機游走的算法, SCI[12]與VGraph[13]是基于模型的算法,而RMOEA[5]與RWECD[14]是基于進化計算的算法.所有對比算法的參數(shù)都與原論文保持一致. 2.1.1 真實網(wǎng)絡(luò)數(shù)據(jù)集 表1給出了以上6個真實網(wǎng)絡(luò)的具體參數(shù)信息. 表1 真實網(wǎng)絡(luò)參數(shù) 在真實網(wǎng)絡(luò)數(shù)據(jù)集實驗上,本文選擇了6個數(shù)據(jù)集進行實驗以驗證FEV-MOEA算法的有效性,分別包含:WebKB[15]中四個美國大學(xué)的計算機交流網(wǎng)絡(luò)Cornell、Texas、Washington、Wisconsin與兩個科學(xué)引用網(wǎng)絡(luò)Cora[16]、Citeseer[16]. 2.1.2 人工網(wǎng)絡(luò)數(shù)據(jù)集 實驗采用LFR[17]網(wǎng)絡(luò)生成工具生成只包含結(jié)構(gòu)信息的人工網(wǎng)絡(luò),利用文獻[18]的方案為每個節(jié)點生成對應(yīng)的屬性信息.兩組具有不同參數(shù)設(shè)置的人工網(wǎng)絡(luò)D1、D2用于驗證算法的有效性,具體參數(shù)及設(shè)置如表2所示,其余未說明的參數(shù)設(shè)置為LFR工具的默認值.D1網(wǎng)絡(luò)側(cè)重于實驗不同的μ值對算法精度的影響,μ值代表社區(qū)的混合程度,μ值越大,則社區(qū)結(jié)構(gòu)越模糊,算法越難劃分出正確的社區(qū).而D2網(wǎng)絡(luò)側(cè)重于實驗不同網(wǎng)絡(luò)規(guī)模變化對算法精度的影響,N值越大,則網(wǎng)絡(luò)規(guī)模越大. 表2 人工網(wǎng)絡(luò)D1、D2的參數(shù)設(shè)置 采用標準互信息NMI[19]與平衡分數(shù)F1[20] 對算法的結(jié)果進行評價.NMI定義如下: (4) NMI度量兩個聚類結(jié)果相似程度的指標,其值在 [0,1] 之間,數(shù)值越大表示聚類結(jié)果越相似.其中,CA、CB分別表示真實社區(qū)劃分與預(yù)測的社區(qū)劃分結(jié)果;Nij表示同時被分配到CA中第i個社區(qū)與CB中第j個社區(qū)的節(jié)點數(shù)量,Ni表示CA中第i個社區(qū)的節(jié)點數(shù)量,Nj表示CB中第j個社區(qū)的節(jié)點數(shù)量. F1 用于衡量算法精確性和召回率的指標,F1定義如下: (5) (6) (7) 式(7)中:F1值在 [0,1]之間,數(shù)值越大表示算法性能越好.TP表示在同一真實社區(qū)的節(jié)點被劃分到相同社區(qū)的節(jié)點對個數(shù),TN表示在不同真實社區(qū)的節(jié)點被劃分到不同社區(qū)的節(jié)點對個數(shù),FP表示在不同真實社區(qū)的節(jié)點被劃分到相同社區(qū)的節(jié)點對個數(shù),FN表示在相同真實社區(qū)的節(jié)點被劃分到不同社區(qū)的節(jié)點對個數(shù). 圖7、圖8分別為FEV-MOEA與其它6種對比算法在不同真實網(wǎng)絡(luò)數(shù)據(jù)集下的精度實驗,其中圖7為NMI精度實驗,圖8為F1精度實驗.實驗結(jié)果表明,FEV-MOEA在各個真實網(wǎng)絡(luò)數(shù)據(jù)集上的精度效果最佳,說明FEV-MOEA算法相較于傳統(tǒng)的社區(qū)發(fā)現(xiàn)算法在屬性網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)上具有更好的精度,這是因為FEV-MOEA算法的編碼方案能夠有效提取每個節(jié)點的屬性與結(jié)構(gòu)信息,并通過后處理修正的策略,提高社區(qū)發(fā)現(xiàn)的精度.其中,DeepWalk、Node2Vec、RMOEA與VGraph算法只考慮了結(jié)構(gòu)信息,因此在各個數(shù)據(jù)集上的效果不佳.而SCI與RWECD算法雖然考慮了屬性信息,但是沒有考慮到網(wǎng)絡(luò)中可能存在著屬性信息與結(jié)構(gòu)信息不匹配的問題,因此雖然精度有所提升,但是也沒有達到較高的精度. 圖7 真實網(wǎng)絡(luò)數(shù)據(jù)集NMI實驗 圖8 真實網(wǎng)絡(luò)數(shù)據(jù)集F1實驗 圖9顯示了FEV-MOEA算法與其它6種對比算法在D1網(wǎng)絡(luò)組上關(guān)于社區(qū)混合參數(shù)μ的精度實驗.從圖9可以看出,所有算法的NMI值都隨著社區(qū)混合參數(shù)μ的增加而減少,這是因為社區(qū)混合參數(shù)μ值越大,說明社區(qū)結(jié)構(gòu)越模糊,算法越難檢測到正確的社區(qū)劃分.FEV-MOEA算法的精度雖然隨著μ值的增加而降低,但是相較于其它比較算法,其精度下降的較為平緩,這是因為即使在面對社區(qū)結(jié)構(gòu)模糊的網(wǎng)絡(luò)時,FEV-MOEA算法通過綜合考慮網(wǎng)絡(luò)中的屬性信息來彌補結(jié)構(gòu)信息的不足,進而提高社區(qū)劃分的精度. 圖9 不同混合參數(shù)μ的實驗結(jié)果 圖10、圖11顯示了FEV-MOEA算法與其它6種對比算法在D2網(wǎng)絡(luò)組上的精度實驗,其中圖10為NMI精度實驗,圖11為F1精度實驗.實驗結(jié)果表明,在各個規(guī)模的數(shù)據(jù)集下,FEV-MOEA算法都保持著最高的精度.網(wǎng)絡(luò)規(guī)模越大意味著網(wǎng)絡(luò)的結(jié)構(gòu)會更加復(fù)雜,而FEV-MOEA算法通過融合節(jié)點的屬性信息與后處理修正策略,能夠在不同規(guī)模的網(wǎng)絡(luò)下保持良好的魯棒性與準確性. 圖10 人工網(wǎng)絡(luò)數(shù)據(jù)集NMI實驗 因此,FEV-MOEA算法隨著網(wǎng)絡(luò)規(guī)模的增加,其精度一直保持在較高的水平并且沒有較大的波動.而其余6種對比算法隨著網(wǎng)絡(luò)規(guī)模的增加,精度波動的幅度較大,說明其魯棒性較差,無法在不同規(guī)模網(wǎng)絡(luò)下進行有效的社區(qū)發(fā)現(xiàn). 本文提出了一種基于融合嵌入向量的多目標優(yōu)化社區(qū)發(fā)現(xiàn)算法FEV-MOEA.與傳統(tǒng)編解碼方案不同,該算法的編解碼方案能夠利用到每個節(jié)點的屬性與結(jié)構(gòu)嵌入向量,使得算法能夠不受到網(wǎng)絡(luò)結(jié)構(gòu)的限制繼而發(fā)現(xiàn)高質(zhì)量的社區(qū).同時,設(shè)計一個后處理社區(qū)修正的策略,使得算法的解能夠克服陷入局部最優(yōu)的問題,提高社區(qū)發(fā)現(xiàn)的精度.通過在真實網(wǎng)絡(luò)和人工網(wǎng)絡(luò)數(shù)據(jù)集上實驗,驗證了FEV-MOEA算法能夠在復(fù)雜屬性網(wǎng)絡(luò)上進行高精度的社區(qū)發(fā)現(xiàn).未來,在現(xiàn)有工作基礎(chǔ)上,針對異構(gòu)網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)展開探索,將異構(gòu)網(wǎng)絡(luò)中不同類型的信息與進化計算相結(jié)合以檢測高質(zhì)量的社區(qū).1.2 FEV-MOEA算法框架
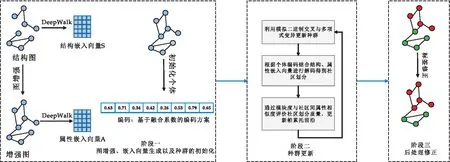
1.3 圖增強、嵌入向量生成及種群初始化
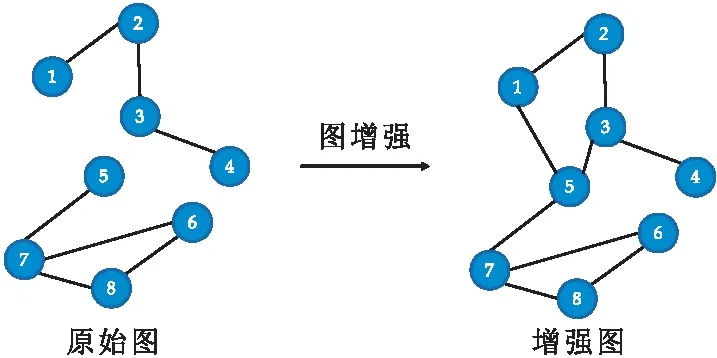
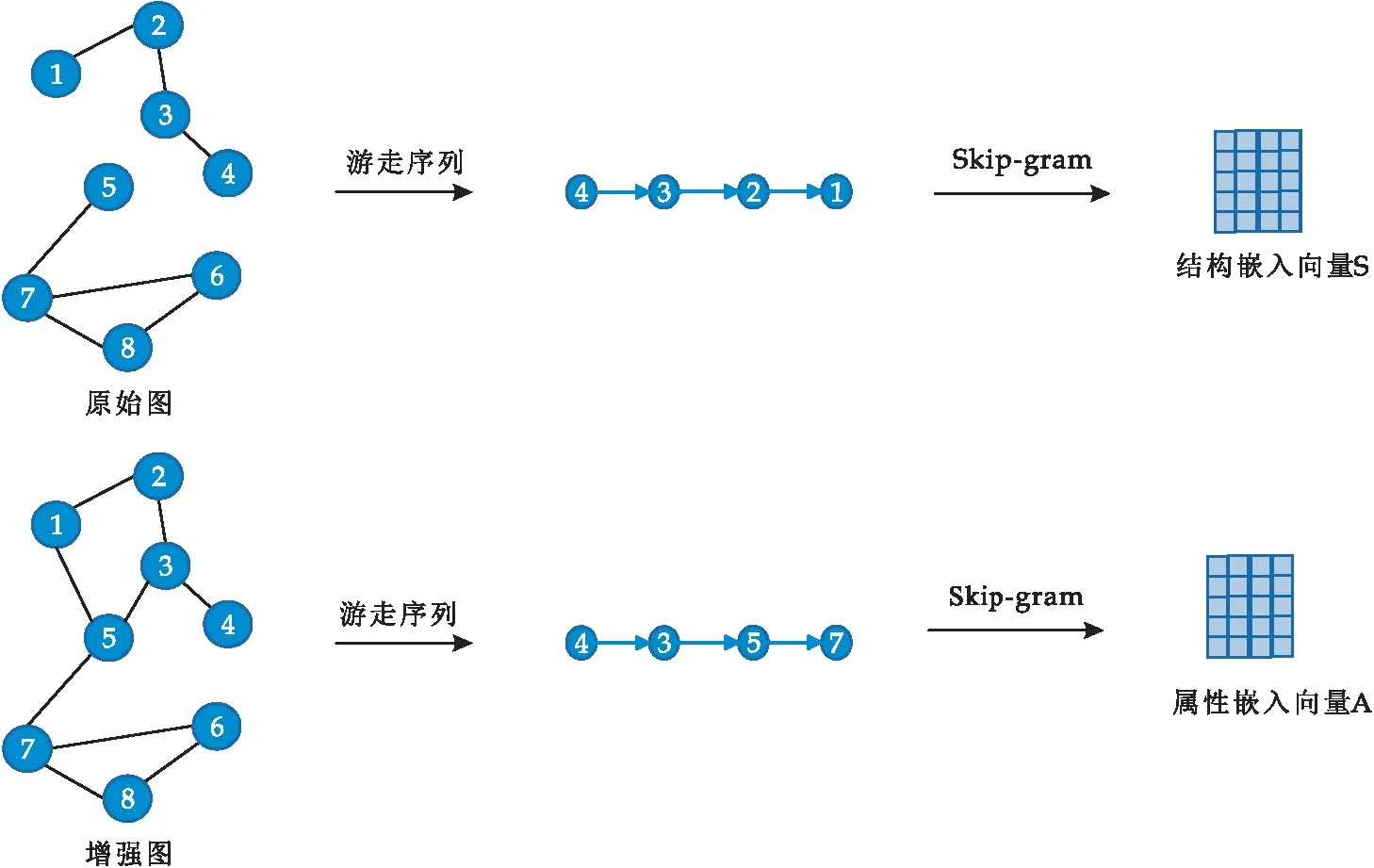
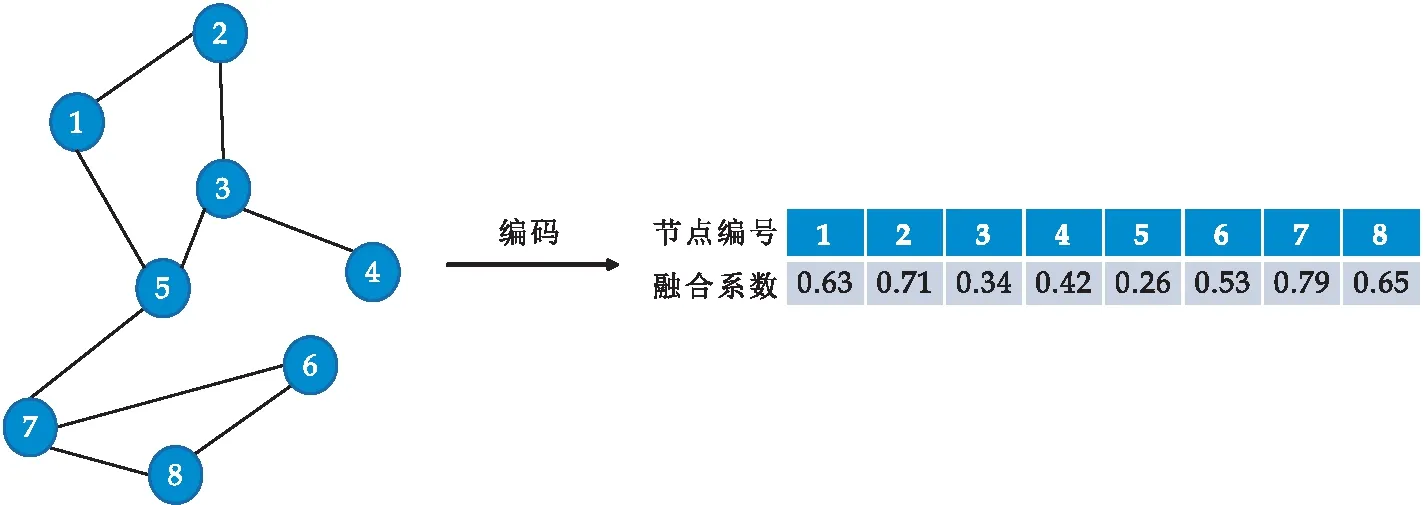

1.4 種群更新
1.5 后處理節(jié)點修正
1.6 算法偽代碼


2 實驗結(jié)果與分析
2.1 實驗數(shù)據(jù)集
2.2 評價指標
2.3 真實網(wǎng)絡(luò)數(shù)據(jù)集實驗結(jié)果
2.4 人工網(wǎng)絡(luò)數(shù)據(jù)集實驗結(jié)果
3 結(jié)論

