新冠疫情下核電廠主控室空調系統運行措施★
劉文斌 周 濤
(1.東南大學能源與環境學院,江蘇 南京 210096; 2.核熱工標準化團隊,江蘇 南京 210096)
2019年12月底以來,一種新型冠狀病毒肺炎爆發,在短短時間內由武漢蔓延至全國各個地區。在身為核電廠核心的主控室中,空調通風系統的運行,加速了空氣在各個區域之間的流動,在使用時間長、室內相對封閉的區域中,存在較大的感染的隱患,可能對核電站的安全運行造成重大影響。對于主控室,黃東山等[1]提出采用集中式空氣凈化配置方案。而在疫情期間,殷婷[2]認為中央空調系統應該盡可能的全新風運行。關于一次回風工況轉換到全新風運行工況,王季樓等[3]提出了需要注意的三個問題為新風管道能否滿足要求,冷水機組需要提供更多的冷量,空調機組的換熱能力。但是未考慮到疫情下室內回風可能會對人體產生健康上的影響。以某核電廠主控室為例,從確保主控室新風安全性的角度入手,進行主控室空調系統研究。對反應堆主控室人員健康及核電站的安全運行有著重要的理論意義和工程價值。
1 研究對象
1.1 幾何模型
某核電廠主控室[4]如圖1所示。

從圖1可以看到,主控室根據不同房間類型分為1個公共控制室、 2個主控制室、2個計算機房、2個管廊間、1個走廊,2個配電柜間。其中,主控室體積(長×寬×高)為14.95×12.15×4.5。以之為例,進行研究。
1.2 設計參數
1.2.1室外設計參數
全廠的室外計算參數宜采用統一的原則或者標準進行考慮,對于核電廠的室外參數可基于GB 50019—2015[5]標準選取。由此查得連云港市室外氣象參數如表1所示。

表1 連云港市室外空調設計參數
1.2.2室內設計參數
根據GB 50736—2012民用建筑供暖通風與空氣調節設計規范[6]。夏季室內空調設計溫度為22 ℃~28 ℃,夏季室內設計相對濕度為40%~65%。室內空調設計參數如表2所示。

表2 室內空調設計參數
2 計算公式
2.1 負荷計算公式
1)外墻的冷負荷計算公式。
CLQ=KFΔtτ-ε
(1)
其中,CLQ為逐時冷負荷,W;K為圍護結構傳熱系數,W/(m2·K);F為墻體的面積,m2;τ為計算時間,h;ε為圍護結構表面受到周期為24 h諧性溫度波作用,溫度波傳到內表面的時間延遲,h;τ-ε為溫度波的作用時間,即溫度波作用于圍護結構內表面的時間,h;Δtτ-ε為作用時刻下,圍護結構的冷負荷計算溫差,簡稱負荷溫差。
2)空調新風冷負荷計算公式。
Q=GW(iW-in)
(2)
其中,GW為新風量,kg/s;iW為室外空氣焓值,kJ/kg;in為室內空氣焓值,kJ/kg。
3)電子設備冷負荷計算公式。
Q=1 000n1n2n3N
(3)
其中,Q為電子設備散熱量,W;N為電子設備的安裝功率,kW;n1為安裝系數,是電子設備設計軸功率與安裝功率之比,一般可取0.7~0.9;n2為負荷功率,是電子設備小時的平均實耗功率與設計軸功率之比;n3為同時使用系數,是房間內電子設備同時使用的安裝功率與總功率之比。
4)照明設備冷負荷計算公式。
照明設備散熱量屬于穩定得熱,一般得熱量是不隨時間變化的。根據照明燈具的類型和安裝方式的不同,其得熱量為:
白熾燈:
Q=1 000N
(4)
熒光燈:
Q=1 000n1n2N
(5)
其中,N為照明燈具所需功率,kW;n1為鎮流器消耗功率系數,在明裝熒光燈的鎮流器裝在空調房間內時,取n1=1.2;在暗裝熒光燈鎮流器設在頂棚內時,取n1=1.0;n2為燈罩隔熱系數,在熒光燈罩上部有小孔(下部為玻璃板),可利用自然通風散熱與熒光燈頂棚內時,取n2=0.5~0.6;在熒光燈罩無通風孔時,則視頂棚內通風情況,n2=0.6~0.8。
5)人體散熱冷負荷計算公式。
人體散熱與性別、年齡、衣著、勞動強度及周圍環境條件等多種因素有關。實際計算中,人體散熱可以以成年男子為基礎,乘以考慮了各類人員組成比例的系數,稱群集系數。人體散熱量為:
Q=qnn′
(6)
其中,q為不同室溫和勞動性質時成年男子散熱量,W;n為室內全部人數;n′為群集系數。
2.2 新風管道風速計算公式
氣流經過風道送/回風口及閥門時會產生很大的再生噪聲,設計時應對風速進行限制。采用假定流速法,對風管內風速進行設定,主管道風速控制在4 m/s~6 m/s范圍內,支管風速控制在3 m/s~5 m/s以內。除必須設置的防火閥和調試用的手動平衡閥外,盡量減少末端調節用風閥。
(7)
其中,Q為送風量,m3/h;V為風速,m/s;a,b均為風管尺寸,mm。
3 計算結果及分析
3.1 冷負荷計算結果
夏季冷負荷采用冷負荷系數法計算逐時負荷,根據公式進行計算,計算結果如表3所示。

表3 冷負荷計算表 W
由表3可看出,墻體存在蓄熱,有著一定的衰減度,故最大冷負荷出現的時刻較晚。燈光夜晚使用較多,照明最大冷負荷出現時刻也較晚,20點時最大。人體、設備、新風負荷等呈現出中間大,兩頭小的趨勢,最大時刻出現在16時左右。房間的最大冷負荷出現在16時,為3 kW,總濕負荷為1.54 kg/h。
3.2 三種全空氣系統處理計算分析
1)15%新風比運行時空氣處理過程。
在新風比為15%時,一次回風空調過程焓濕圖見圖2。

從圖2得到,對于一次回風系統,組合式空調器處理總新風量為330 m3/h,按照新風比15%計算,則需要送入主控室內的新風量為49.5 m3/h。室內設計溫度25 ℃, 相對濕度55%,室外干球溫度32.7 ℃,濕球溫度27.8 ℃,新風比為15%,送風溫度15 ℃,采用露點送風。只考慮一個主控室,通過查圖計算,送風焓值為32.8 kJ/kg,一次回風(15%新風比)混合點焓值為57 kJ/kg,室外焓值為89.2 kJ/kg。一次回風(15%新風比)系統送風時冷源需提供的冷量為49.5×1.162×(57-32.8)/3 600=0.39 kW。
2)40%新風比運行時空氣處理過程。
在新風比為40%時,一次回風空調過程焓濕圖見圖3。

從圖3得到,按照新風比40%計算,則需要送入主控室內的新風量為132 m3/h; 一次回風(40%新風比)系統送風時冷源需提供的冷量132×1.162×(62.1-32.5)/3 600=1.26 kW。
3)全新風運行時空氣處理過程。
全新風空調過程焓濕圖如圖4所示。
從圖4得到,按照全新風送風,則送風量為330 m3/h。全新風系統進行送風時冷源需提供的冷量330×1.134×(89.2-32.8)/3 600=5.65 kW。在送風量不變的條件下,空調系統改用40%新風比運行送風消耗的冷量將是原有冷量的3.32倍,改用全新風運行送風消耗的冷量將是原有冷量的14.8倍。全新風運行送風需要的冷量已經超過一般冷水機組的運行能力。因此需要對表冷器等進行改造,提高制冷量。

3.3 新風管道風速對比分析
根據式(7)進行計算,得到主干管尺寸設計以及管內流速情況如表4所示。
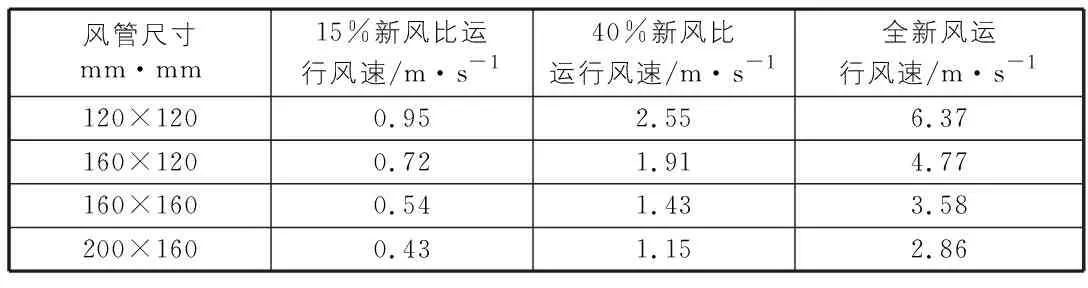
表4 風管尺寸及空氣流速表
從表4得到,增大新風比和采用全新風運行會使得原風管內風速增大,但是尚未超出太多。因此,出于安全考慮,最好改用全新風運行。東南大學錢華等[12]在“呼吸道傳染病空氣傳播的感染概率的預測模型”一文中提到除特別極端的案例,通風都能夠有效降低感染率,大的通風量不僅能夠快速稀釋感染者所呼出的飛沫核從而降低感染率,而且能夠快速移除室內污染物使得室內污染物濃度能夠快速下降。此外,為防止風速過大,造成能量損失和噪聲,可對風管進行局部改造,如增設靜壓箱,風管局部加粗,增加消音措施等。對于其他改造方案,若必須采用空調回風時,按最大新風量運行時,新回風比宜大于40%,且應加裝凈化消毒裝置。
4 結論
疫情期間,從確保主控室新風安全性的角度入手,通過計算比較全新風工況運行和一次回風工況運行設備冷量和新風管道能否滿足,得出主控室空調系統運行的措施:
1)對于主控室空調系統,采用全新風運行,減小感染幾率。2)如果未能開窗(如本項目),應在外墻的適當位置設置相應風量的排風扇,或啟用排煙風機。3)空調系統啟用前應進行清洗、消毒,并經衛生學評價合格,同時,應確保新風來源清潔,新風應直接取自室外,禁止從機房、樓道和天棚吊頂內取風。空調系統內定時噴灑霧化稀釋的消毒劑。

