薄壁梁剪切撓曲性能解耦分析方法研究

周茂定，藺鵬臻，張元海

(1.甘肅農業大學 土木工程系，甘肅 蘭州 730070；2.蘭州交通大學 土木工程學院，甘肅 蘭州 730070)

薄壁梁結構廣泛應用于現代橋梁及結構工程中,剪切變形作為其撓曲力學特性的重要影響因素一直受國內外學者的廣泛關注。文獻[1-12]論述了關于T形、箱形薄壁梁的剪力滯、剪切變形等相關研究成果。這些研究文獻中常采用翼板位移差函數作為廣義位移來分析薄壁結構的剪力滯效應[2-6],部分學者[7-9]通過引入Timoshenko梁理論來反映薄壁梁的腹板剪切變形。翼板剪力滯[4]和腹板剪切變形[7]本質均是由壁板的面內剪切變形引起,可統稱為剪切效應。在分析剪切廣義位移時,文獻[2-12]常將其與初等梁撓曲混為一起,導致分析過程相對復雜。文獻[13-16]選取剪切引起的撓度作為獨立變形狀態,使得薄壁結構的剪切撓曲分析具有明確的物理意義,但分析過程仍以能量變分法[4-16]為基礎。利用該法獲得廣義位移的控制微分方程多為復雜的高次方程。同時,該法也很難適用連續梁的剪切撓曲分析,導致該法不能廣泛應用于實際工程。我國JTG 3362—2018《公路鋼筋混凝土及預應力混凝土橋涵設計規范》[17]采用有效寬度來考慮T形及箱形梁的剪力滯效應。該方法雖然分析簡便,但不能精確獲得撓曲應力沿翼板的實際分布,也不能獲得薄壁梁的精確撓度。因此還需尋求適合工程應用且精度較高的簡化分析方法。文獻[11-13]在研究箱梁懸臂板和頂板剪力滯翹曲位移時發現兩者剪應變存在一定差異,進而導致剪切翹曲應力的求解不夠準確。遺憾的是上述文獻并未明確給出翹曲應力修正的表達式。

本文從薄壁梁各壁板的應變與位移關系出發,建立一種具有明晰力學機理的撓曲位移函數。選取剪切撓度為廣義位移,通過解耦撓曲性能建立剪切撓度及剪切翹曲應力的簡化分析公式,并給出翼板翹曲應力的合理修正公式。然后,利用中支點變形連續條件導出薄壁連續梁的簡化分析方法。最后通過數值算例驗證本文方法的有效性及求解精度。

1 薄壁梁截面剪切撓曲函數分析

1.1 坐標系及基本假設

選取受任意荷載p(z)的簡支對稱工字梁結構見圖1,采用正交直角坐標系,x和y軸為橫截面的形心主軸,z軸為梁縱軸。對于組成薄壁梁截面的各壁板,可認為其應力沿壁厚均勻分布。因此,建立沿各壁板中心線的流動坐標系n-s-z,流動坐標s以順時針方向為正,n為各平面的法向坐標,見圖1(b)。圖1(b)中,a、b表示工字梁上、下翼板的半寬;ha、hb為形心至上、下翼板厚中心的距離;h為梁高;t為截面各壁厚度。

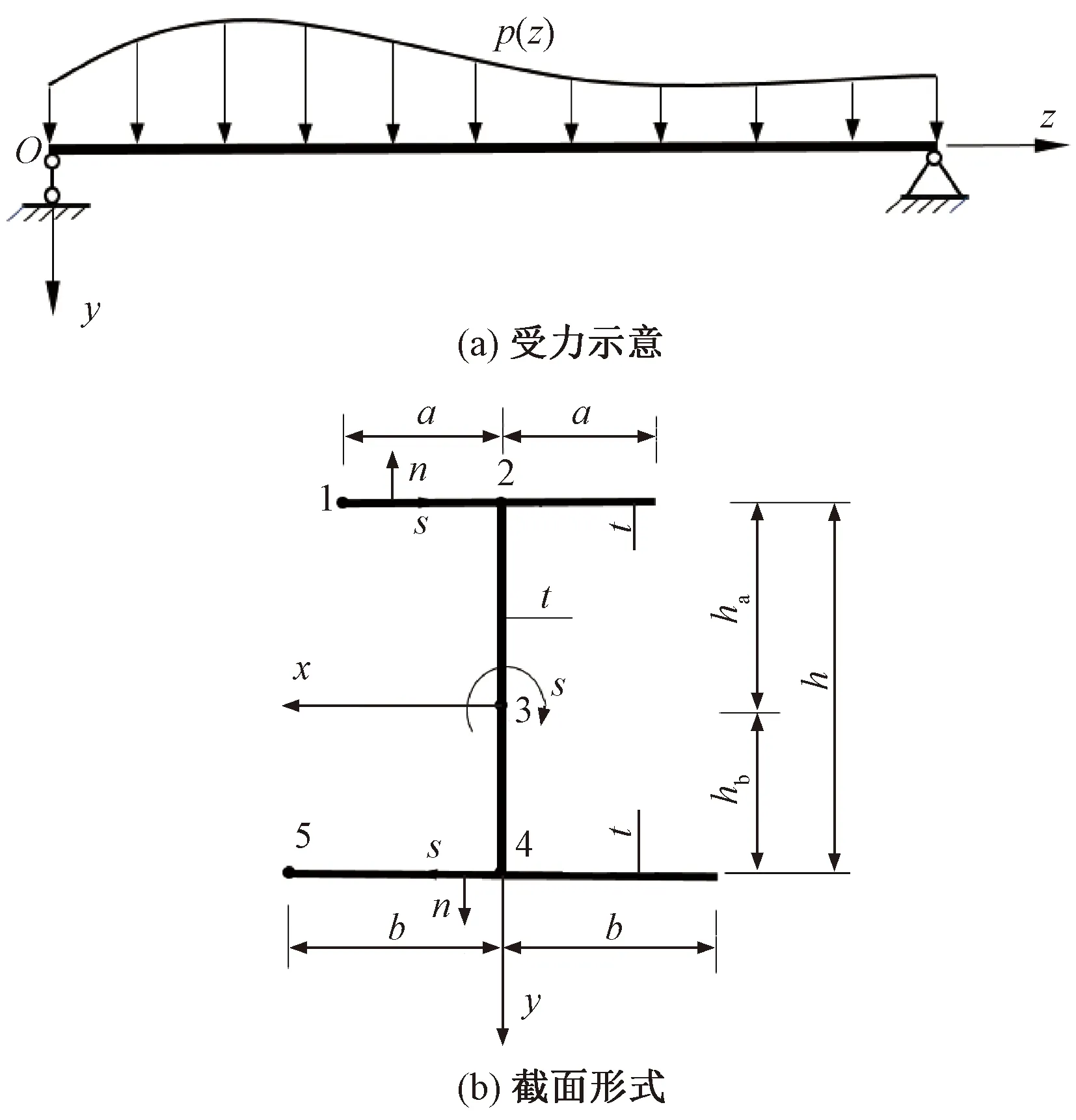
圖1 受均布荷載的簡支梁

在小變形條件下,薄壁梁截面保持剛性不變形[17],忽略各壁板的面外剪切變形和正應力。若用u表示z軸位移,v表示周向s軸位移,基于上述假設可知,截面各壁板將滿足彈性理論中的平面應力方程[18]。因此,各壁板平面內的位移分量與變形分量之間關系為[18]

( 1 )

( 2 )

式中:εz為梁軸向應變;γsz為各壁板的面內剪切應變。

1.2 考慮剪切變形影響的撓曲分析

對于薄壁梁翼板,由截面的剛性不變形可知v沿z軸保持不變,即?v/?z=0。根據剪應力表達式及式( 2 )可得分別由u2(z)與u4(z)表示的工字梁上、下翼板的縱向位移ua、ub[10,15]表達式分別為

( 3 )

( 4 )

顯然,u2(z)和u4(z)點也是腹板頂、底部的縱向位移。根據薄壁梁彎曲理論[17]可求得工字梁腹板3點(形心處)的剪應力為

( 5 )

式中:A為薄壁梁截面面積;Aa為梁上翼板面積;α1為腹板剪切系數。

由式( 5 )可得腹板的任意點的剪應力τw為

( 6 )

由式( 2 )與式( 6 )可求得梁腹板的剪應變γw為

( 7 )

若令w1(z)表示薄壁梁考慮剪切變形影響的豎向位移,則w′1(z)=?v/?z。從3點起對式( 7 )關于s進行積分,并轉化為y坐標可得腹板的縱向撓曲位移uw為

( 8 )

式中:α2稱為腹板翹曲系數,α2=1/(3A);u3(z)為積分起點常數。

顯然,由式( 8 )可表示縱向位移u2(z)和u4(z)。綜合式( 3 )、式( 4 )及式( 8 ),可求得薄壁梁截面的撓曲縱向位移u的表達式為

u(x,y,z)=-yw′1(z)+[α1y-α2y3+α3(x)]·

( 9 )

式中:α3(z)稱為翼板剪切翹曲函數,其表達式為

(10)

式( 9 )為考慮剪切變形影響時,薄壁梁截面的縱向位移函數。對于單軸對稱的薄壁箱梁[15-16]、T梁考慮剪切變形的位移函數分析過程與工字梁相同,在此不在贅述。

2 截面平衡條件分析

梁的豎向位移分解見圖2。若將梁的撓曲位移w1(z)分解為初等梁撓曲w0(z)與剪切撓曲ws(z)兩種變形狀態,則有

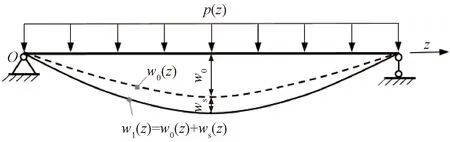
圖2 梁的豎向位移分解

w1(z)=w0(z)+ws(z)

(11)

將式(11)代入式( 9 )中,再由式( 1 )及胡可定理可得梁截面的正應力σ為

σ(x,y,z)=-yEw″0(z)-yEw″s(z)+[α1y-α2y3+

(12)

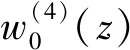
顯然,式(12)右端第1項為初等梁理論下截面的正應力σ0。若仍保持w0滿足初等梁理論下撓曲內力平衡,則σ0沿全截面不合成軸力,且σ0以y為力臂合成截面的彎矩M。因此,式(12)右端其余項則為剪切翹曲應力σs,其沿截面不合成軸力,且以y為力臂不合成力矩,即

yEw″s(z)+Eu′3(z)

(13)

(14)

(15)

將式(13)代入式(14)中化簡整理后可得

(16)

式中:α41與α42分別稱為腹板與翼板剪切修正系數,其表達式為

(17)

(18)

其中,Ab為下翼板的面積。

式(16)兩邊關于z積分便可求得含有積分常數的u3(z)表達式,而由于彈性小變形假設忽略梁軸線伸長,即截面不產生剛體位移,因而積分常數為0。將式(16)代入式(13)后,再代入式(15)可得

(19)

式中:系數λ=Ix/Iyα,Ix為梁截面慣性矩,Iyα可稱為剪切慣性積,其表達式為

(20)

根據式(19)的關系,結合式( 9 )可得剪切翹曲縱向位移us為

us(x,y,z)=-ω(x,y)w′s(z)

(21)

式中:ω(x,y)為剪切翹曲位移函數,ω(x,y)=y-λα(x,y),α(x,y)=yα1-y3α2+α3(x)+α4。

對于其他單軸對稱的箱形、T形面分析過程與工字梁相似,差異為截面參數值的不同。

3 簡化分析方法及翹曲應力的修正

求解剪切撓曲位移的經典方法是根據式(21)及能量變分法[4-16]可導出ws的控制微分方程為

(22)

式中:k為剪切常數,其表達式為

(23)

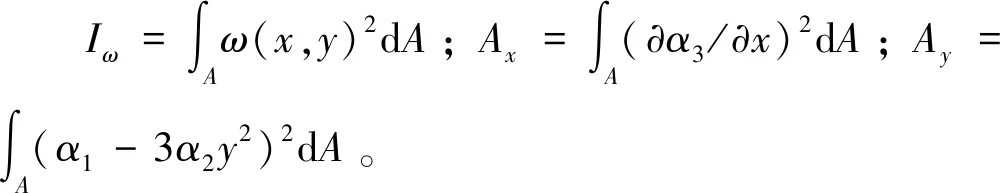
3.1 靜定梁的簡化分析方法

剪切翹曲控制微分方程式(22)的求解相對復雜,且由于解析表達式較為復雜,對連續梁很難得到解析式,而限制其工程應用。因此,本文將提出新的簡化分析方法。

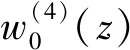
(24)

式中:μ為泊松比,由E/(2G)=1+μ得出。

根據式(19)及其與截面縱向位移的關系積分可得截面的剪切撓度ws為

(25)

式中:D為積分常數,需根據薄壁梁剪切撓度ws的邊界條件確定。

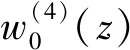
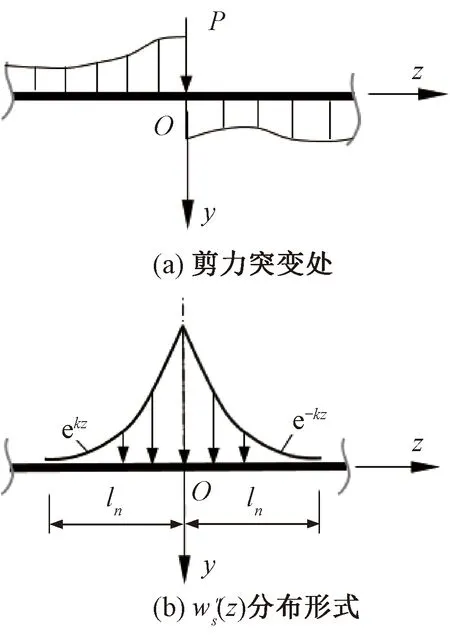
圖3 剪力不連續點等效分析

在分析剪切撓曲變形狀態時,將圖3(a)中的集中荷載P轉化為分布荷載p(z)分析。通過分析撓曲微分方程式(22)的解可知[14-15],w″s(z)在剪力不連續點分別以ekz和e-kz的形式對稱分布于P的兩側(如圖3(b)所示)。而由式(24)可知,p(z)的分布形式將與w″s(z)相同,設P的等效分布荷載集度為

p(z)=βPe-kz。

(26)

式中:β為分布荷載集度系數。

由于工程常用梁的等效分布荷載的主要影響范圍ln較小,梁長相對ln可近似認為是∞。對y軸以右的分布荷載進行積分必然為合力P/2,從而可求得β為0.5k,從而可求得剪力不連續點的等效分布荷載。

3.2 連續梁的簡化方法

對圖4(a)所示的多跨連續梁,中支點的剪切支反力即為剪力不連續點的集中荷載P1-i(i=1,2,…)見圖4(b)。值得注意的是,剪切支反力與初等梁的支反力不同。在結構力學中求解P1-i的常用方法是根據連續梁中支點剪切撓度ws為0的條件,列方程組求解各支點的剪切反力,從而求解進一步分析剪切變形。

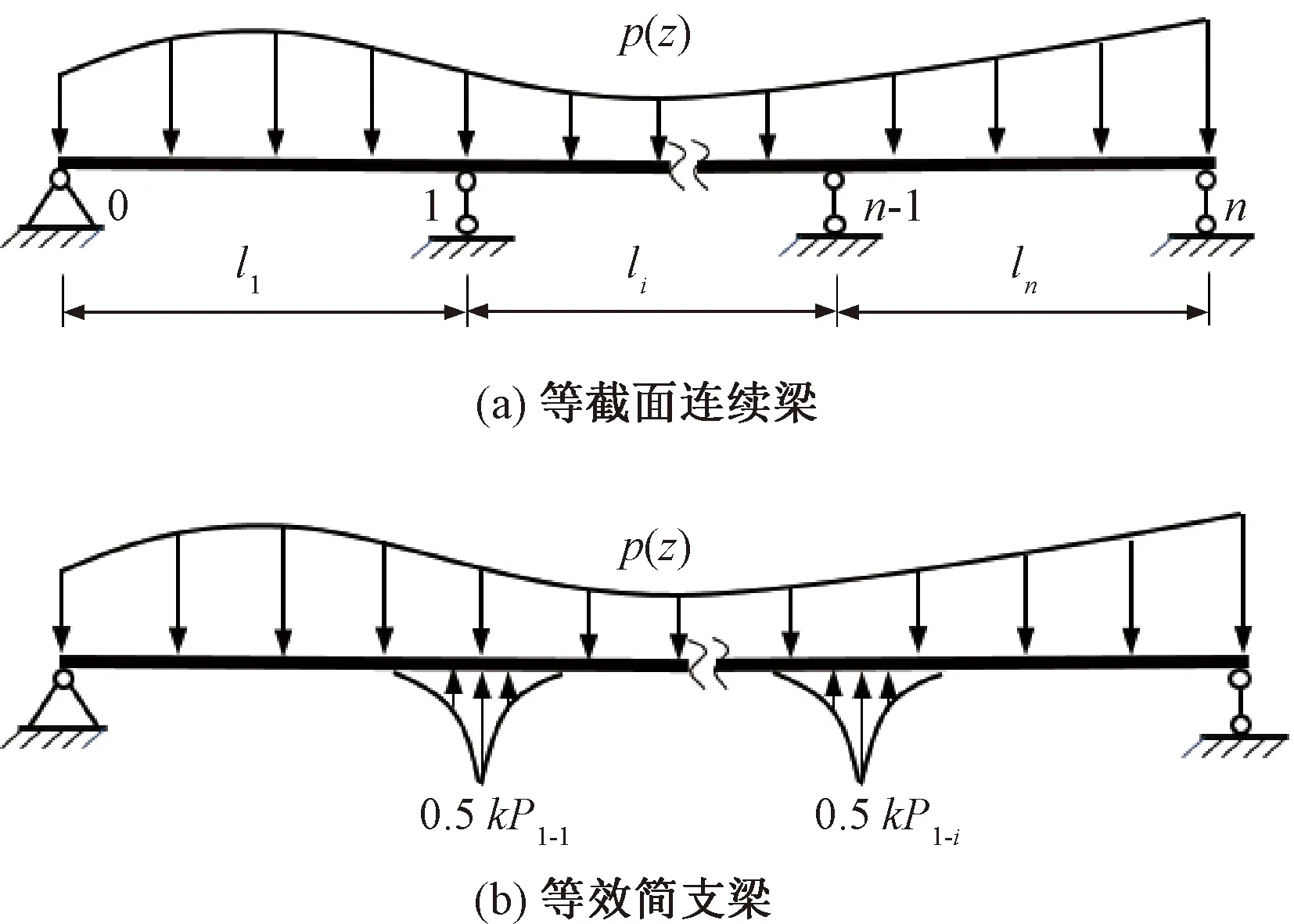
圖4 連續梁中支點的等效轉換

然而,上述分析方法涉及復雜方程組的求解,分析過程十分復雜。由式(25)可知,連續梁邊支點剪切撓度為0,使得積分常數D必然為0。因此,在中支點處ws=0的條件將轉化為該點的彎矩為0,進而連續梁的剪切撓曲將轉為多跨簡支梁形式,見圖5(a)。當忽略剪切支反力P1-i的分布荷載對梁彎矩影響時,可近似為圖5(b)所示簡支梁進行分析。

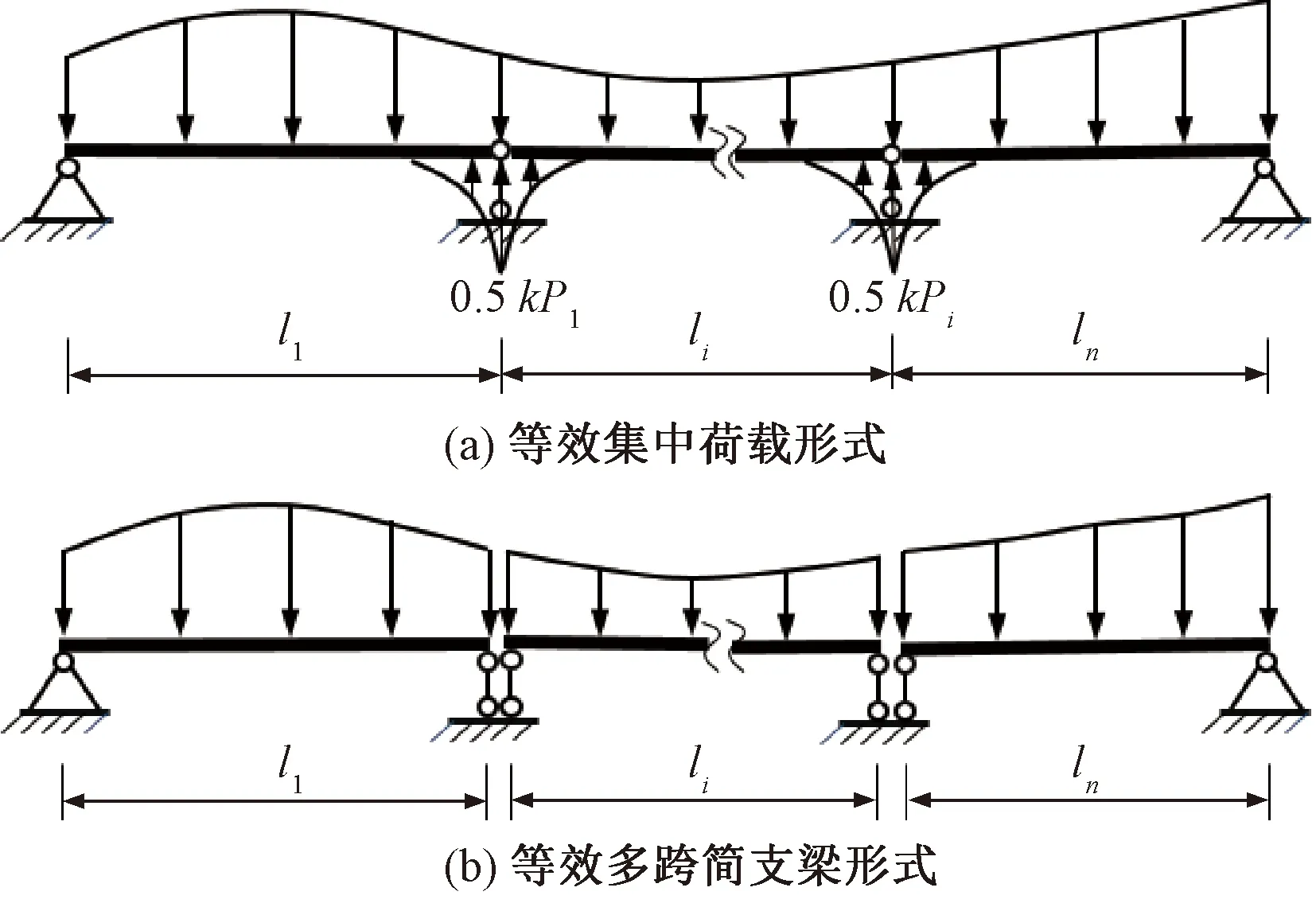
圖5 連續梁的簡化轉換

3.3 剪切翹曲應力的修正

為驗證上述簡化理論的求解精度,以文獻[19]承受均布荷載q的簡支矩形截面梁為例進行分析。設梁厚t0=1,高度h。由式(24)～式(25)可求得的剪切撓度ws與翹曲應力為σs分別為

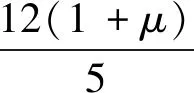
(27)

(28)

按照彈性平面梁[18]理論計算表達為

(29)

(30)

對比式(27)、式(28)與式(29)、式(30)可知,按本文簡化方法計算所得的剪切撓度與彈性理論解相比為24(1+μ)/(24+15μ)。實際工程中由于泊松比μ在0.1～0.3之間,對于剪切撓度的差異在1.03～1.09之間,其差異可以忽略。剪切翹曲應力式(28)與式(30)相比,則多1+μ的系數。該對比結果與文獻[20]的研究結論相同,即如果板條承受沿邊緣線的拉力時,泊松比對彎曲應力無影響,如該矩形平面梁,若板條受到邊緣之間拉伸荷載作用時,需考慮泊松比影響,如工字梁、箱梁的翼板承受腹板傳遞的剪力。因此,翼板的剪切翹曲應力需進一步修正。

由文獻[20]的研究成果,當水平板條承受板縱向的線性拉伸(壓縮)荷載qz時,見圖6,板條的縱向修正翹曲應力σc與未修正翹曲應力σu分別為

刺史呂某……致祭于蘇升、陳寅、李寬、秦陳甫、魯余之靈。爾等五人感余誠信，力輸公稅，爭赴先期。溪山阻深，淫潦暴至，不忍欺我，忘其險艱。[6]6372

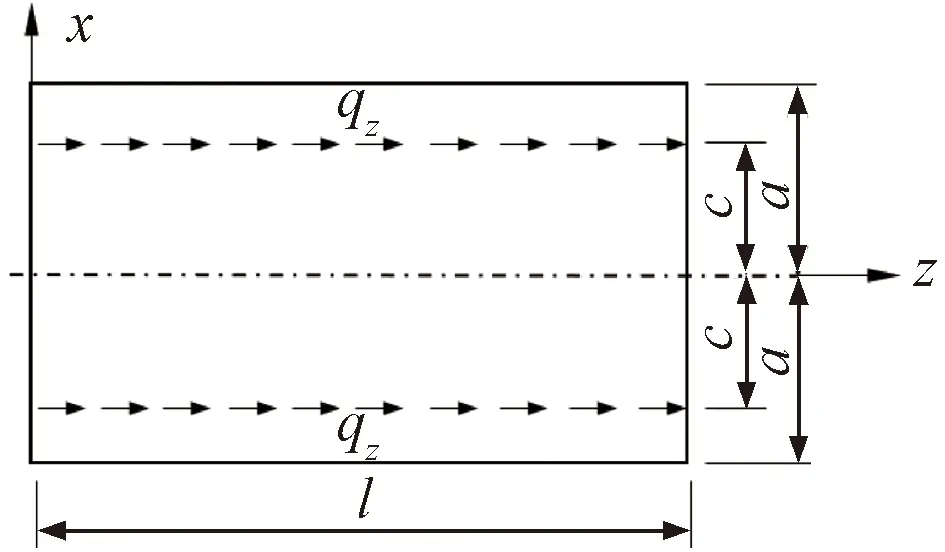
圖6 矩形板條受線性拉伸荷載

σc(χ,z)=-(2+μ)[1-3(1-φ)2-3χ2-

(31)

σu(χ,z)=-(2+μ)[1-3(1-φ)2-3χ2|+

(32)

式中:φ=c/a,a為翼板寬,c為剪力作用點;χ=x/a;ξ為平面板的截面的常數;“∣”表示選擇,當0≤x≤c(-c≤x≤0)時,豎線后面不考慮,當c≤x≤a(-a≤x≤-c)時,則豎線取消;對于薄壁梁的翼板,qz即相當于截面腹板傳遞給翼板的剪力。

利用該平面板條的翹曲應力式(31)和式(32)的應力差比來對本文所得的翹曲應力進行修正。定義翹曲應力的修正系數為ψ,其表示用修正的翹曲應力式(31)計算翼板的板寬范圍翹曲應力差與用式(32)計算的翹曲應力差之比。

對圖1(b)所示截面,荷載作用點為c=0,即φ=0。分別用式(31)與式(32)計算翼板χ=0與χ=1處的翹曲應力之差分別為Δσc與Δσu,則ψ為

(33)

若用Δσs表示按式(24)計算的翼板在χ=0與χ=1處應力差,如圖7點劃線,則實際應力差Δσc=ψΔσs。

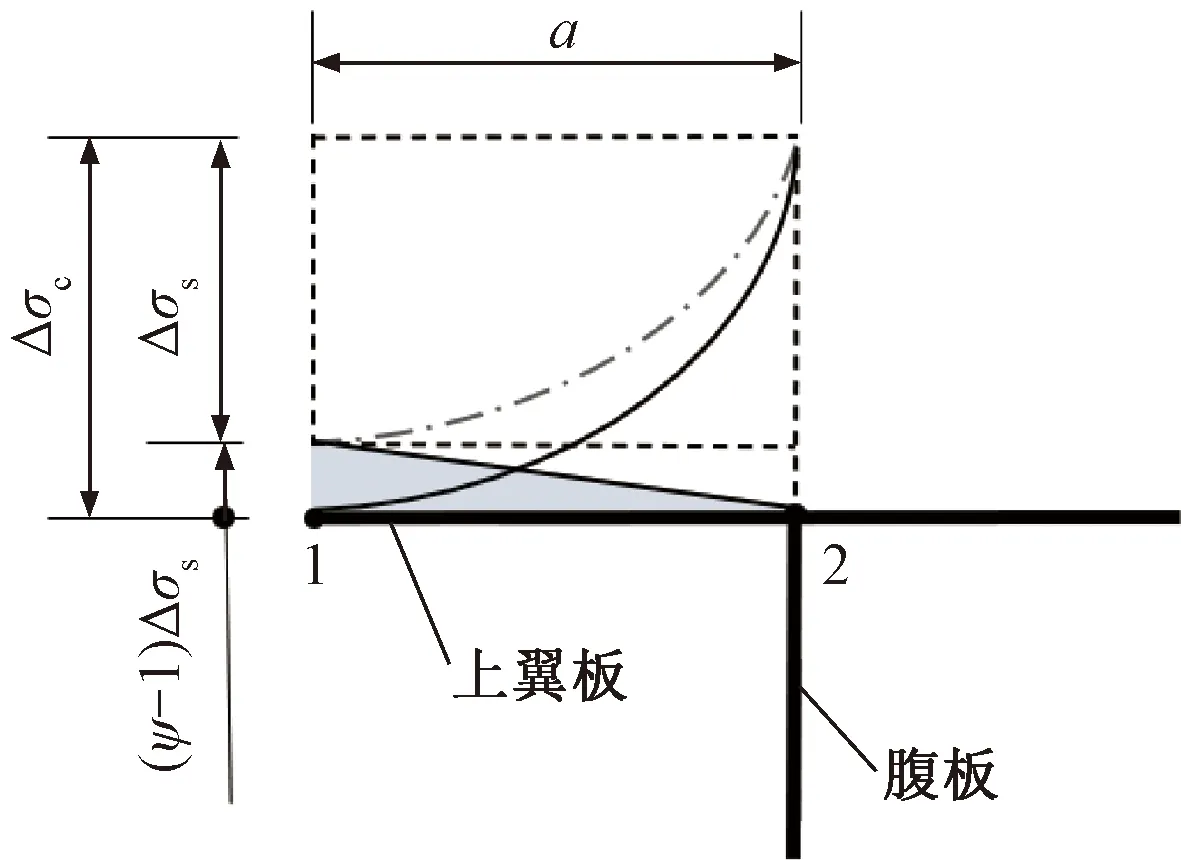
圖7 剪切翹曲應力的修正

同樣,對于荷載作用于閉口箱梁腹板(φ=1)時,翼板的修正系數ψ值為

(34)

對于帶懸臂板的箱梁截面,閉口頂、底板的修正系數與式(34)相同,而開口懸臂板的修正系數ψ值為

(35)

4 數值算例

4.1 剪切翹曲應力修正系數分析

為驗證本文提出翹曲應力修正方法的正確性,以文獻[4,11-12]中帶懸臂板的箱梁算例為對象,進行分析。根據文獻算例給出的φ和μ值,分別計算頂板、懸臂板的應力差值比系數ψ1和ψ2。利用ψ1和ψ2計算兩板的應力差值比η。作為對比,基于文獻[4,11-12]的空間有限元應力結果,計算懸臂板與頂板的應力差值比ηFEM,計算結果見表1。表1中,η0為未修正翹曲應力的差值比,η0=(1-φ)2/φ2;η=η0(ψ2/ψ1)。

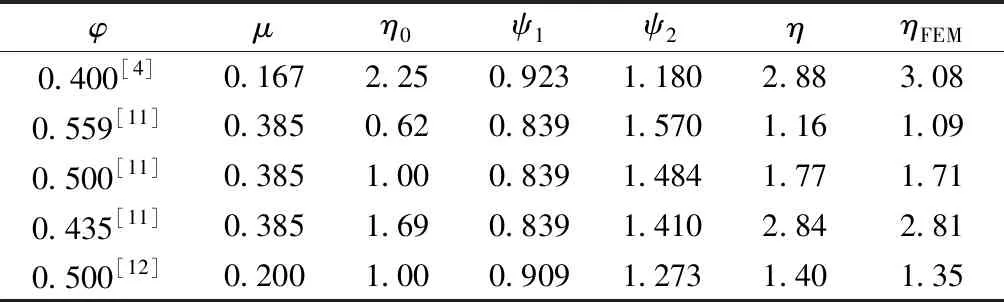
表1 應力差值系數及差值比分析

對比表1中不同板寬比和不同材料泊松比下,η與ηFEM的分析結果可知,本文方法獲得應力差值比與空間有限元結果吻合較好,可說明式(33)～式(35)計算的應力修正系數ψ可靠性較強。對比未修的翹曲應力差值比η0與ηFEM可知,兩者差異較大。通過表1的分析,并結合式(33)～式(35)可知,翹曲應力修正系數與板寬比φ和材料泊松比μ均有關。

4.2 簡支梁撓曲分析

以圖1所示的簡支工字型截面梁為例進行分析。設截面的上、翼板寬a=b=100 mm,厚度均為6 mm;腹板高h=200 mm,厚度為16 mm;梁的跨度l=800 mm,材料的彈性模量為3 000 MPa,泊松比μ分別設為0、0.2和0.385。均布荷載作用于全梁腹板頂部,荷載值為p=10 N/mm。

作為對比驗證,選用Ansys中的Shell63殼單元建立該簡支梁的空間有限元模型(3D FEM)。全橋以四邊長為10 mm的單元進行劃分,共劃分為4 800個單元和4 941個節點。采用簡化方法及3D FEM分別計算材料泊松比為0、0.2、0.385時,跨中截面上半翼板的撓曲應力結果見表2。為減小荷載作用處應力集中的影響,表1中FEM結果為截面上、下翼板應力的平均值。

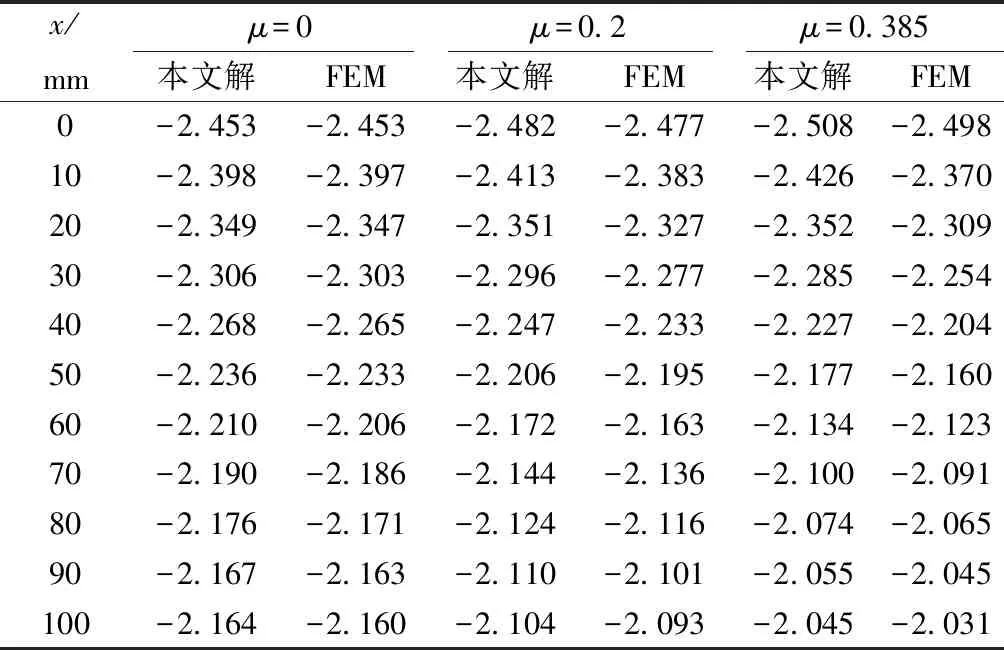
表2 上半翼板的撓曲應力 MPa

對比表2中不同材料泊松比所對應的撓曲應力可知:材料泊松比μ對翼板的撓曲應力結果有一定影響;材料泊松比μ對翼板的撓曲應力差有影響。因此,在求解薄壁梁翼板應力時需考慮泊松比影響。對比不同材料泊松比下本文方法所得應力與FEM結果可知,當μ=0時,兩者應力最大誤差為2.3‰;當μ=0.2時,兩者應力最大誤差為1.2%;當μ=0.385時,兩者應力最大誤差為2.3%。通過上述分析可得采用本文簡化方法可得到較為精確的撓曲應力。

為驗證簡化分析方法對撓度計算的適用性,分別按初等梁理論、簡化方法及3D FEM計算簡支薄壁梁的撓度曲線見圖8。

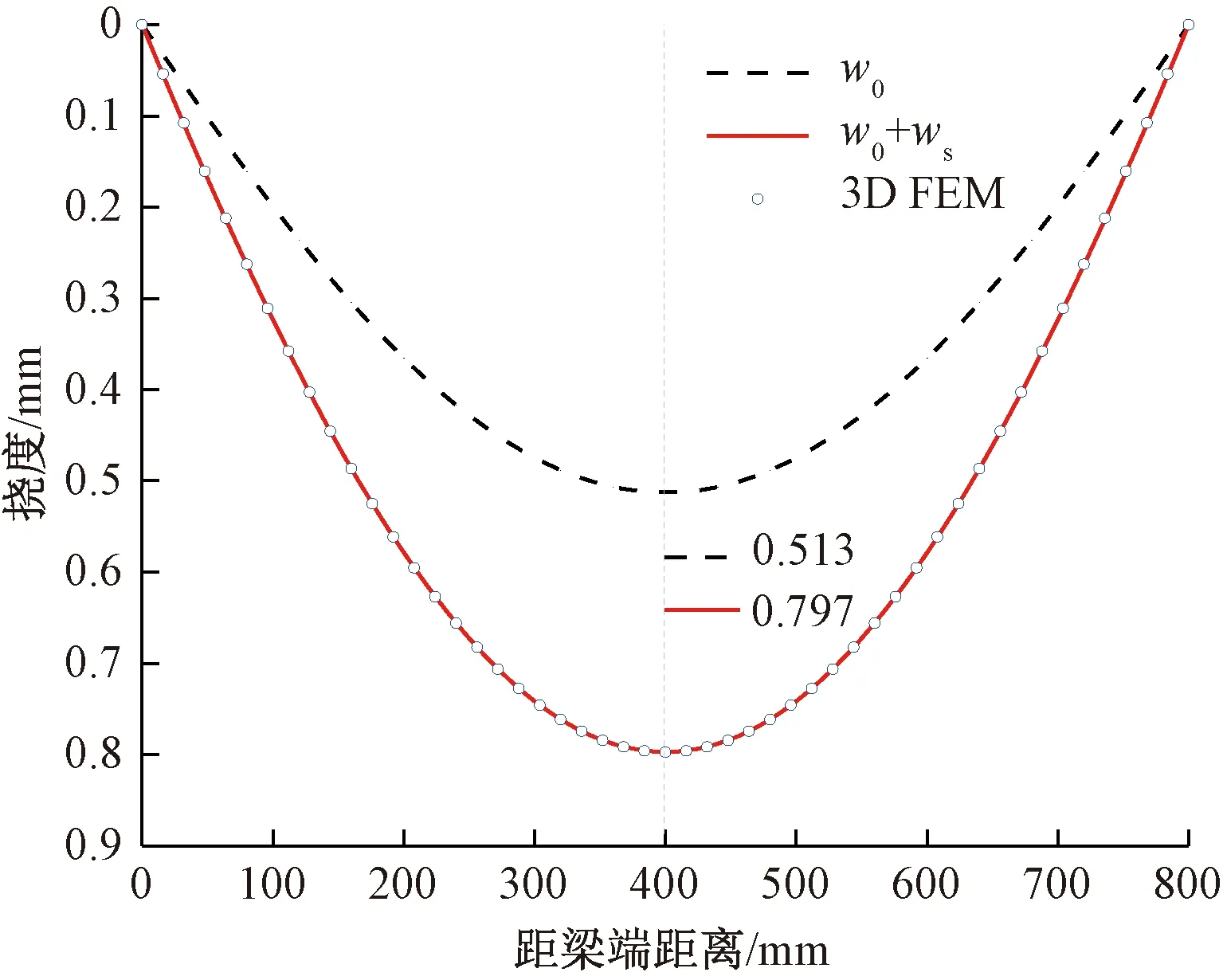
圖8 荷載作用下的撓度曲線

對比觀察圖8可知,按照簡化方式計算的撓度值與3D FEM結果吻合良好,說明本文方法求解撓度精度較高。在均布荷載作用下,剪切撓度為初等梁撓度的0.55倍,可見剪切變形對薄壁梁的撓度影響較大。

4.3 連續梁的撓曲分析

為驗證本文提出的連續梁簡化分析方法的有效性,選取4.2節中截面尺寸,連續梁的跨徑組合為(1 000+1 200+1 000)mm。材料參數和4.2節相同,泊松比設為0.385。承受的荷載工況為:均布荷載p=10 N/mm;邊跨、中跨的跨中部均承受集中荷載P=5 kN。按照3.2節所述的簡化方法求解連續梁在工況1、2荷載下中支點的剪切支反力值P1和P2。同時,采用變分法[14]求解剪切支反力,并將上述方法求得的剪切支反力見表3。表3中,差值比=(簡化計算值-精確值)/精確值。

表3 中支點的剪切支反力

由表3差值比結果可知,按照簡化分析方式求得剪切支反力與精確值相差在3%以內。顯然,按照簡化方式可以滿足工程要求。

為驗證簡化分析方式求解連續梁應力的準確性,不同荷載下簡化分析方法與空間有限元(3D FEM)方式求得的腹板頂點應力縱向分布結果見圖9。

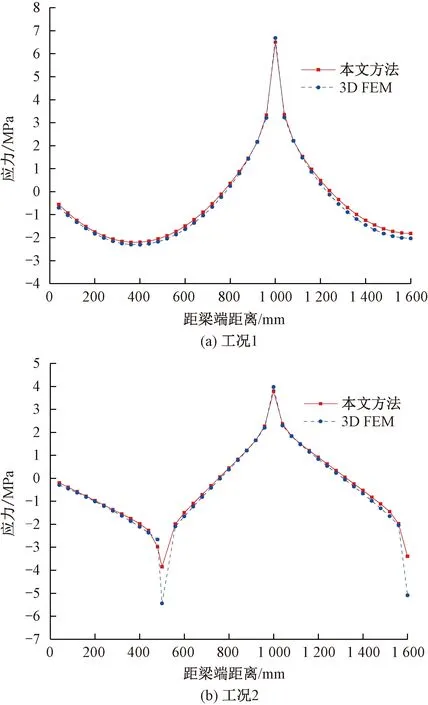
圖9 不同荷載條件下腹板頂點應力沿梁軸的分布圖

由圖9可知,除去圖9(b)中集中荷載作用處截面,其余各截面采用本文簡化方法求得的應力與3D FEM結果吻合良好。集中荷載處截面的差異是因應力集中導致。通過對比分析結果可說明簡化方式求得連續梁的應力具有足夠精度。

表4分別給出了采用本文簡化方法、精確方法[14]與3D FEM方式計算的連續梁邊跨和中跨跨中截面的撓度結果。表4中,wJs與ws分別為精確解與簡化方法所得的剪切撓度,差值比=(wJs-ws)/(3D FEM)。

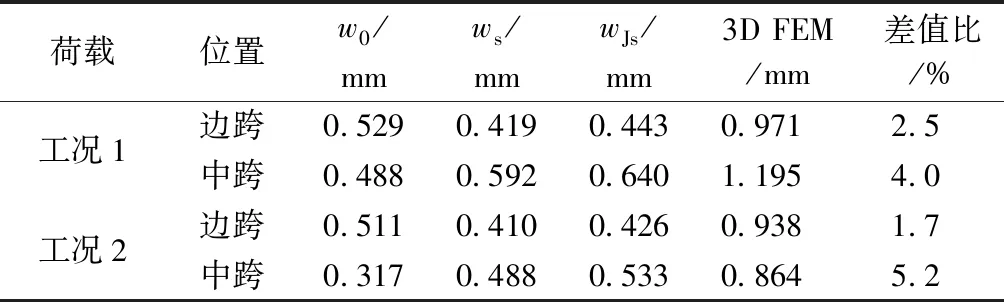
表4 跨中撓度對比

由表4的對比分析可知,按照兩種方法計算的薄壁梁跨中撓度與3D FEM的計算結果均吻合良好,采用本文簡化方式與精確方法計算的撓度相差均在6%以內,說明簡化方法精度滿足工程要求;工況1荷載下,邊跨剪切撓度約為初等梁撓度的0.84倍,中跨約為1.31倍;工況2荷載下,邊跨剪切撓度約為初等梁撓度的0.83倍,中跨約為1.68倍;對比簡支梁結果可知,剪切變形對連續梁的影響更為重要。

5 結論

1)從薄壁梁各壁板的剪切應變與位移的關系出發,導出考慮剪切變形影響的撓曲位移函數。選取剪切變形引起的撓度為獨立位移,通過解耦撓曲性能獲得了剪切撓度與翹曲應力的簡化公式。

2)基于平面板條的應力分析結果,導出薄壁梁翼板翹曲應力的修正計算式。利用中支點變形連續條件,給出連續梁的剪切撓曲簡化分析方法。

3)與傳統分析方法相比,本文方法求解過程簡便,且對連續梁的適用性較強,便于在實際工程應用。

4)數值算例表明,本文方法求得的應力結果與3D FEM結果最大誤差在3%以內,撓最大誤差為6%以內,說明本文方法可靠且精度較高;材料的泊松比及板寬比對薄壁梁翼板的翹曲應力影響較大。