不同壓實狀態淺季凍區膨脹土力學特性的凍融演化規律

王亮亮，王照騰，田建勝，林宇亮，于明暉

(1.中國礦業大學 深部巖土力學與地下工程國家重點實驗室，江蘇 徐州 221116；2.中國礦業大學 力學與土木工程學院，江蘇 徐州 221116；3.中南大學 土木工程學院，湖南 長沙 410075)

膨脹土是一種富含脹縮性蒙脫石、伊利石等礦物成分的特殊黏性土[1],常因其濕脹干縮特性而導致邊坡破壞、構筑物損失等病害[2],在我國20多個省市和地區均有分布[3-4]。隨著我國北方基礎設施建設加速進行,遭遇的季節性凍土區膨脹土工程問題日趨增多。受反復濕脹干縮與凍脹融縮影響,膨脹土邊坡及其防護體系病害呈現出發生早、比例高、反復性等特點[5];北疆某輸水渠道膨脹土邊坡因“凍融”“干濕”引起強度衰減從而導致滑坡問題頻發[6]。

周期性凍融作用下膨脹土力學性能衰減問題引起了巖土工作者的重視,并成為膨脹土的研究方向之一。文獻[7-9]發現不同初始濕度狀態下的膨脹土無側限抗壓強度,彈性模量在凍融循環作用下存在不可忽視的衰減現象。甘發達[10]發現延吉飽和弱膨脹土在周期性凍融循環作用下,出現大量的裂縫,靜強度、彈性模量、抗剪強度、內摩擦角、黏聚力均發生衰減,且圍壓越大,靜強度、彈性模量越大。Lu等[11]發現周期性凍融作用下南水北調線路某路塹邊坡膨脹土無側限壓縮應力-應變關系呈現為“軟化型”,在首次凍融循環后彈性模量和破壞強度衰減顯著。Tang等[12]采用擾動狀態概念,建立凍融作用下膨脹土的應力-應變統一量化表征模型。Cong等[13]以佳木斯膨脹土為研究對象,發現凍融循環后膨脹土的應力松弛特性,并基于擾動狀態概念提出了膨脹土凍融循環應力松弛模型。Zhao等[14]根據齊齊哈爾膨脹土的干濕與凍融共同作用壓縮試驗成果,利用Konder雙曲線模型建立了考慮凍融循環、干濕循環及其耦合作用影響的歸一化應力-應變曲線。此外,部分學者發現在膨脹土中添加水泥[15]、鋼渣粉水泥[16]、相變材料[17]等可以有效抑制因凍融導致的土體強度衰減。

綜上所述,現有研究主要集中在深季節性凍土區(如新疆、東北地區)膨脹土工程特性隨凍融循環演化方面,而淺季節性凍土區膨脹土工程特性的凍融效應尚未引起關注。以河南平頂山地區為代表的淺季節凍土區夏季綿長、炎熱、潮濕;冬季氣溫相對較低,常有降雪,雖然一年中氣溫通常在-3～31 ℃之間變化,但極端低溫卻時有發生,統計資料顯示,在1999年—2021年間出現3次-15 ℃極端低溫。盡管地處氣候邊緣地帶的極端低溫重現間隔周期較長,但這種非連續性的凍融作用同樣會對淺表層膨脹土力學行為造成影響[18],工程建設中若忽視這種影響必將降低邊坡防護措施的有效性,特別是對高速鐵路的安全運營造成潛在風險,亟待開展研究。

為此,開展不同壓實系數(0.85、0.90、0.95)膨脹土在反復凍結融化作用下的力學行為演化規律研究,并基于Konder雙曲線模型構建周期性凍融作用下膨脹土應力差與應變關系的量化表征模型,為淺季凍區膨脹土相關工程建設提供數據支撐[19]。

1 試樣制備及試驗方案

1.1 重塑膨脹土試樣制備

試驗所用膨脹土為取自位于氣候邊緣地帶的平頂山地區,土體顏色為棕紅～黃褐色且間夾雜色黏性土,含豆狀鐵錳質結核(平均粒徑約10～40 mm)。原位土體總體處于硬塑、堅硬狀態,取樣過程中土體極易沿夾雜礦物界面分離。自由膨脹率測試均值為75%,土樣蒙脫石含量測試結果為8%～17.5%,具有一定的波動性。根據TB 10038—2012《鐵路工程特殊巖土勘察規程》[20]分類標準,擬將土體膨脹性等級判定為弱至中等膨脹性[21](可結合工程項目的重要性,從安全角度綜合選用)。采用單次靜壓成型法制備標準三軸試樣,膨脹土凍融試驗方案見表1。

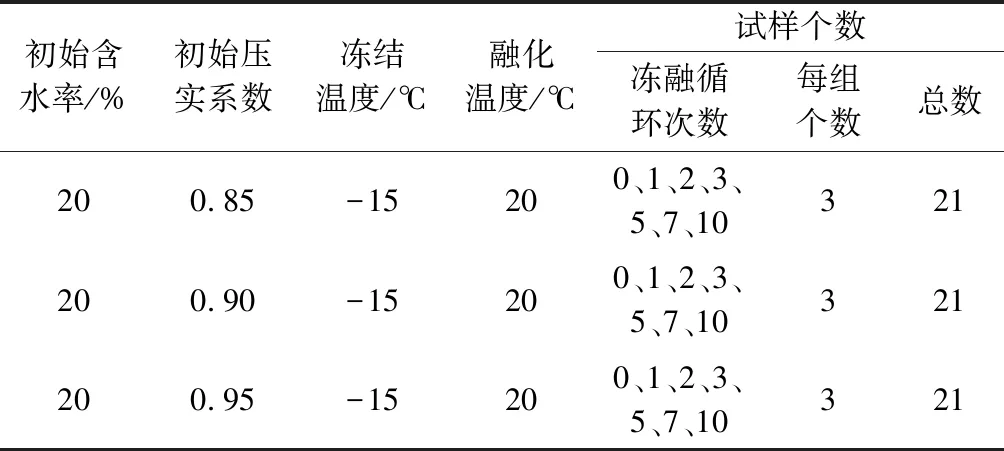
表1 膨脹土凍融試驗方案

1.2 試驗方案

1)凍融溫度邊界值確定。河南省平頂山地區近20年來1月極端氣溫變化曲線見圖1。由圖1可知,當地環境極端氣溫為-15～-6 ℃,考慮到凍融循環可能會對淺層膨脹土的工程特性造成影響及最不利凍融條件,以-15 ℃作為凍結溫度,以20 ℃作為融化溫度。

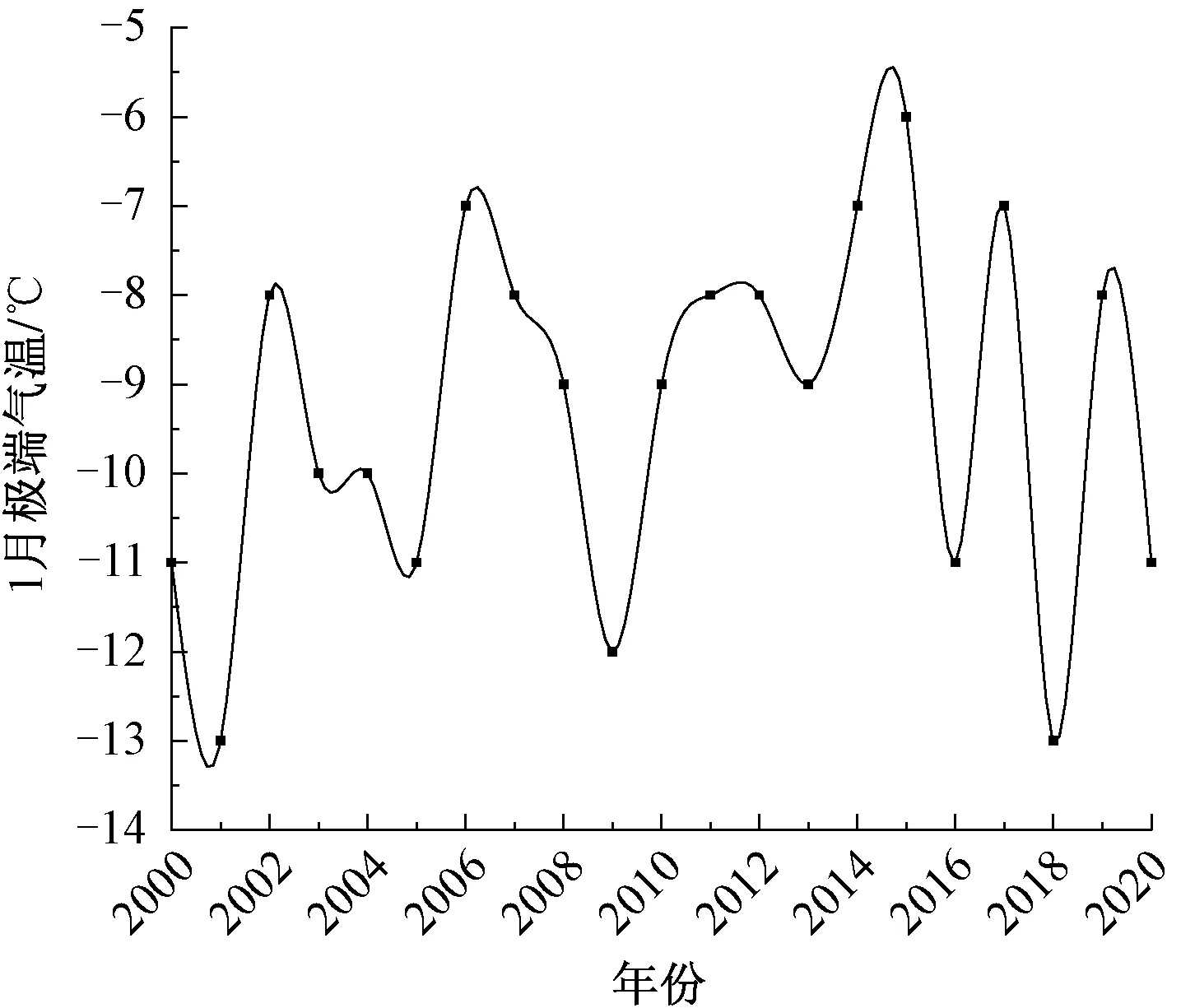
圖1 平頂山地區1月極端氣溫

不同密實狀態膨脹土內摩擦角隨凍融次數的發展規律見圖5(b)。由圖5(b)可知,土體經歷的凍融次數相同時,內摩擦角隨著壓實系數的增加而大幅度提高,初始狀態試樣(NFT=0)的內摩擦角分別為10.03°(k=0.85)、14.87°(k=0.90)、15.85°(k=0.95);不同密實狀態下的土體內摩擦角均在前3次凍融過程中存在較大幅度波動現象,但第4次凍融循環后呈現出相對穩定的增長趨勢,且壓實系數越大,增幅越小;經過10次凍融循環后內摩擦角的增長幅度分別為29.3%(k=0.85)、15.3%(k=0.90)、10.3%(k=0.95)。內摩擦角增大的原因可能是膨脹土試樣在經凍融循環后,試樣顆粒之間產生大量微裂紋,且壓實系數越小微裂紋越多,在三軸壓縮剪切過程中,土顆粒之間的咬合、嵌鎖現象增強,出現土體內摩擦角增大的現象。

不同密實狀態膨脹土抗剪強度參數隨凍融次數發展規律見圖5(a)。由圖5(a)可知,不同密實狀態膨脹土黏聚力隨著凍融循環作用的衰減趨勢總體相似,膨脹土的黏聚力c為

3)三軸剪切試驗。為了避免排水固結與周期性凍融作用產生交互作用,對試樣力學性能造成影響,故采用TSZ-6型全自動三軸儀在100、200、300 kPa三種圍壓下對未凍融、不同凍融次數后的膨脹土試樣進行剪切試驗(UU)。加載速率為0.8 mm/min且軸向應變達到20%時試驗結束。并按照相關試驗規程繪制應力-應變曲線,計算經歷不同凍融次數后膨脹土的破壞強度σf、彈性模量E、抗剪強度指標φ。

2 試驗結果分析

2.1 膨脹土應力-應變關系隨壓實系數與凍融次數變化規律

設上行和下行的彈性系數α=0.3，β=0.2，分別在無突發事件、價格穩定和價格隨機突等多種狀況下，運用Wolfram Mathematic判斷供應鏈的協調狀況，并計算供應鏈各企業的期望收益和最優策略，相關計算結果見表1.

今天，隨著科學技術的發展，印刷業又迎來了“數與網”時代，互聯網、移動互聯網改變著信息傳播和呈現的途徑、方式和手段，傳統紙媒體產業發展不斷受到沖擊和嚴峻挑戰，市場需求空間被不斷壓縮和蠶食。不僅如此，傳統印刷產業在經歷了20世紀的黃金發展期后，已進入產能相對過剩、產業轉型、技術升級、經濟增長方式發生重大變化、增速放緩等多重因素影響的關鍵時期。這種形勢，使為數不少的印刷從業者陷入迷茫狀態，傳統印刷企業如何應對這種局面，下一步究竟如何發展，印刷產業新的發展道路在哪里？這是印刷產業界急需進行深入研究并作出回答的問題。

“嘿嘿，太平本是將軍定，哪個將軍見太平？本將軍平定天下，功高勞苦，想不到功勞越大，越是不能安享太平。”將軍苦笑之余，頹然問道，“沉淵樓什么時候也肯殺忠臣良將了？”

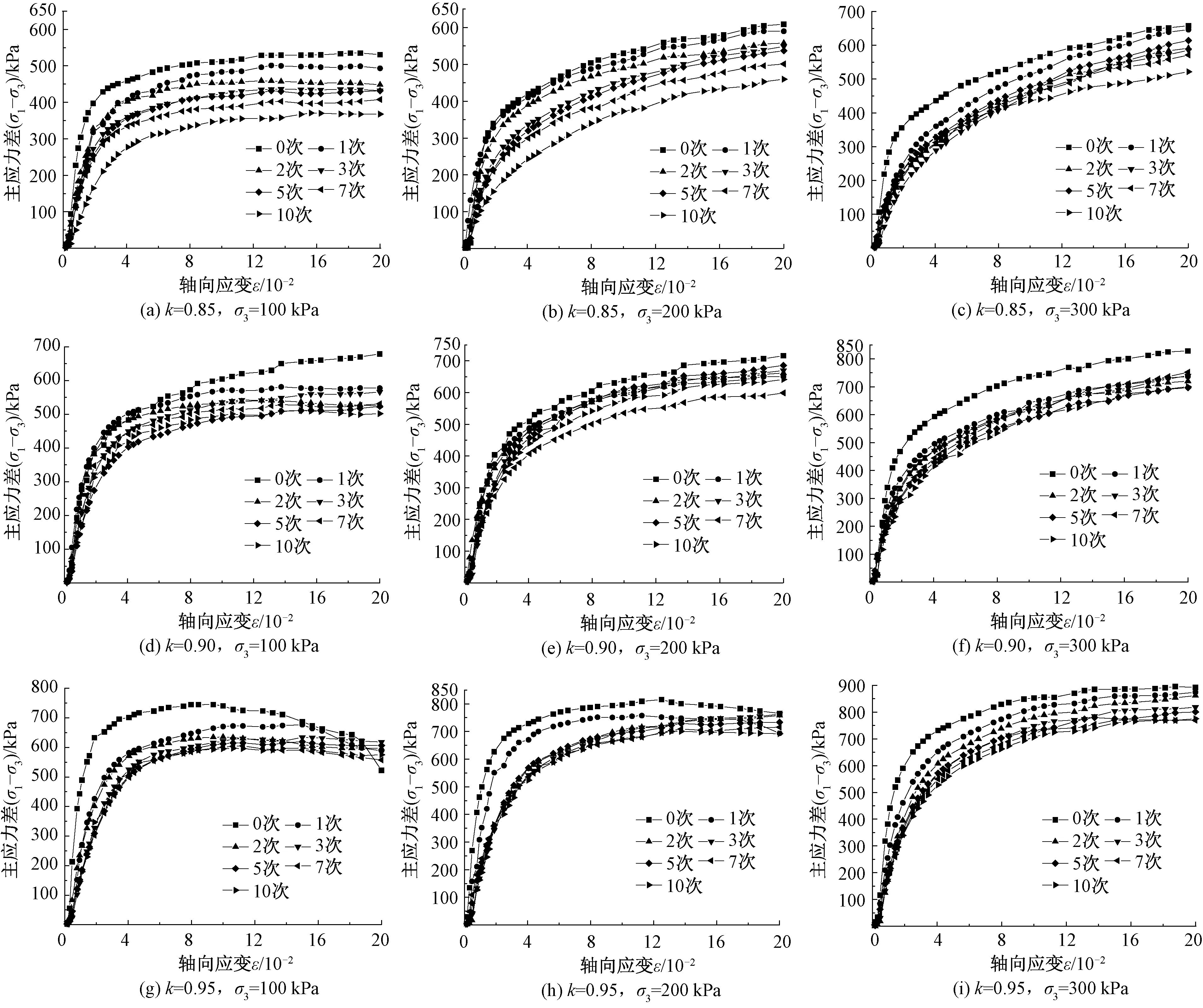
圖2 不同密實狀態下膨脹土(σ1-σ3)～ε曲線隨凍融循環的發展規律

2.2 不同密實狀態膨脹土破壞強度隨凍融循環的變化規律

破壞強度是表征土體極限承載能力的重要指標,應力-應變關系曲線存在明顯峰值時以曲線峰值點對應的應力作為破壞強度,或應力-應變關系曲線為“硬化型”時取軸向應變15%對應的應力值作為破壞強度。不同壓實系數膨脹土破壞強度σf與凍融次數NFT關系曲線見圖3。由圖3可知,膨脹土破壞強度隨凍融次數增長的衰減規律總體上相似,根據試驗獲得的土體破壞強度σf為

土體三軸剪切試驗(UU)應力-應變曲線通常有應變硬化型、應變軟化型及理想彈塑性3種類型。為了得到周期性凍融循環作用下膨脹土應力-應變關系表征模型,以初始壓實系數為0.90的試驗組為例,進行統一化處理。由圖2(d)～圖2(f)可知,在初始壓實系數為0.90的試樣應力-應變曲線均為應變硬化型曲線,其關系可以采用Konder提出的雙曲線模型進行描述,其表達式為

由圖3可知:經過相同凍融次數的膨脹土破壞強度隨著圍壓、初始壓實系數的增加而逐漸增大;較低初始壓實系數k=0.85時,σf與NFT關系曲線近似呈指數型負相關性。經過10次凍融循環后,破壞強度衰減為未凍融試樣的69.4%(σ3=100 kPa)、74.6%(σ3=200 kPa)、78.7%(σ3=300 kPa)。高初始壓實系數k=0.90、0.95時,首次凍融作用導致的膨脹土破壞強度衰減幅度最大,但這種衰減幅度隨著土體初始壓實系數k增加而逐漸縮小;k=0.90時首次凍融衰減幅度分別為12.2%(σ3=100 kPa)、9.3%(σ3=200 kPa)、12.1%(σ3=300 kPa),k=0.95時首次衰減幅度分別為9.2%(σ3=100 kPa)、7.1%(σ3=200 kPa)、5.9%(σ3=300 kPa);經過10次凍融作用后,破壞強度僅為初始狀態的77.6%～89.8%(k=0.90),80.3%～85.9%(k=0.95)。不同密實狀態下膨脹土破壞強度與凍融次數關系曲線擬合結果見表2。

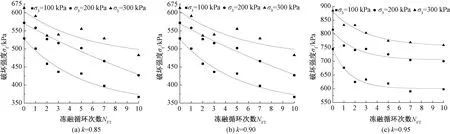
圖3 不同初始壓實系數下膨脹土破壞強度隨凍融次數的變化規律

σf=A+Be-NFT/C

( 1 )

式中:A、B、C均為試驗數據擬合參數;NFT為凍融循環次數。

馬克思指出，人們的“需要即他們的本性”，“你自己的本質即你的需要”。所以說，需要是工程師恪守工程倫理，進行工程創新的動力，是他們實現全面發展的源泉。工程師從事工程活動不僅為了滿足自己生活資料的需要，而且也是為了滿足精神層面和社會層面的需要。基于此，在工程倫理教育中，要偏重于精神的需要，培養工程師的“普世”情懷，讓他們在工程活動中心系“廣大民眾”，以民眾的最大福祉為工程活動的出發點。讓他們的心理需要和心理特征與大眾融合，讓他們的活動迎合社會的基本價值觀念，使工程活動在滿足人類需要的同時，實現工程最大的“善”，即工程與人、自然、社會的和諧共生。這才是工程倫理教育最終的歸宿。

采用SPSS15.0統計學軟件對本研究所有數據進行統計、分析，（±s）表示計量資料，采用t檢驗，率（%）表示計數資料，采用χ2檢驗，差異有明顯統計學意義以P＜0.05表示。

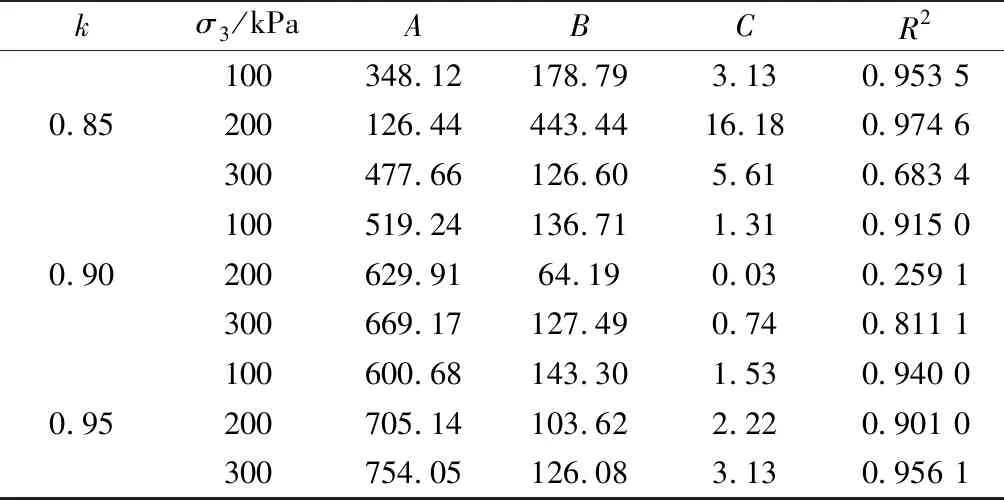
表2 膨脹土破壞強度與凍融次數擬合關系

2.3 不同密實狀態膨脹土彈性模量隨凍融循環的變化規律

彈性模量進行邊坡穩定性分析與防護支擋結構設計計算時的重要指標之一[18]。依據Lee等[23]、胡田飛等[24]的研究成果,并結合凍融循環后膨脹土應力-應變曲線特點,采用(σ1-σ3)～ε關系曲線起點與軸向應變ε=1%所對應應力曲線點之間的斜率作為彈性模量。不同初始壓實系數下膨脹土彈性模量隨凍融次數與圍壓的發展規律見圖4,由圖4可知:高初始壓實系數k=0.95時,膨脹土彈性模量在首次凍融循環后衰減幅度最大,為32.43%(σ3=300 kPa)～48.07%(σ3=100 kPa);彈性模量衰減幅度最為顯著的是前3次凍融循環,5～10次凍融循環過程中,衰減幅度逐漸降低且開始逐漸趨于穩定;10次凍融作用后彈性模量隨著圍壓增加而增大,而其衰減幅度卻隨圍壓增加逐漸減小,即50.67%(σ3=300 kPa)～65.32%(σ3=100 kPa)。隨著壓實系數降低為0.85和0.90時,在周期性凍融作用下,膨脹土試樣彈性模量波動幅度增大;前5次凍融作用是導致彈性模量衰減的主要原因,而后凍融循環過程中,彈性模量衰減幅度逐漸減小;在10次凍融循環后,彈性模量尚未穩定,其中,當k=0.85時,為初始狀態的59.42%(σ3=100 kPa)、90.31%(σ3=200 kPa)、80.56%(σ3=300 kPa),當k=0.90時,為初始狀態的62.35%(σ3=100 kPa)、65.92%(σ3=200 kPa)、57.96%(σ3=300 kPa)。

各密實狀態下膨脹土(σ1-σ3)～ε關系曲線隨凍融過程的變化規律見圖2。圖2中,σ1為軸向應力;σ3為圍壓;σ1-σ3為主應力差;k為壓實系數。由圖2可知:①k=0.85、0.90的試驗組膨脹土主應力差隨軸向應變的發展曲線簇呈現“應變硬化型”,且圍壓越大,硬化趨勢越強;k=0.95的試驗組膨脹土(σ1-σ3)～ε線簇在低圍壓時為弱“應變軟化型”,并隨著圍壓增大逐漸過渡為弱“應變硬化型”;②圍壓不變時相同軸向應變對應的主應力差總體上隨著初始壓實系數的增加而增大;③同一壓實系數的膨脹土,相同軸向應變對應的主應力差隨凍融次數增加而減小,應力衰減幅度隨凍融次數增加而逐次降低,但這種逐次衰減幅度幾乎不受土體初始壓實系數的影響。

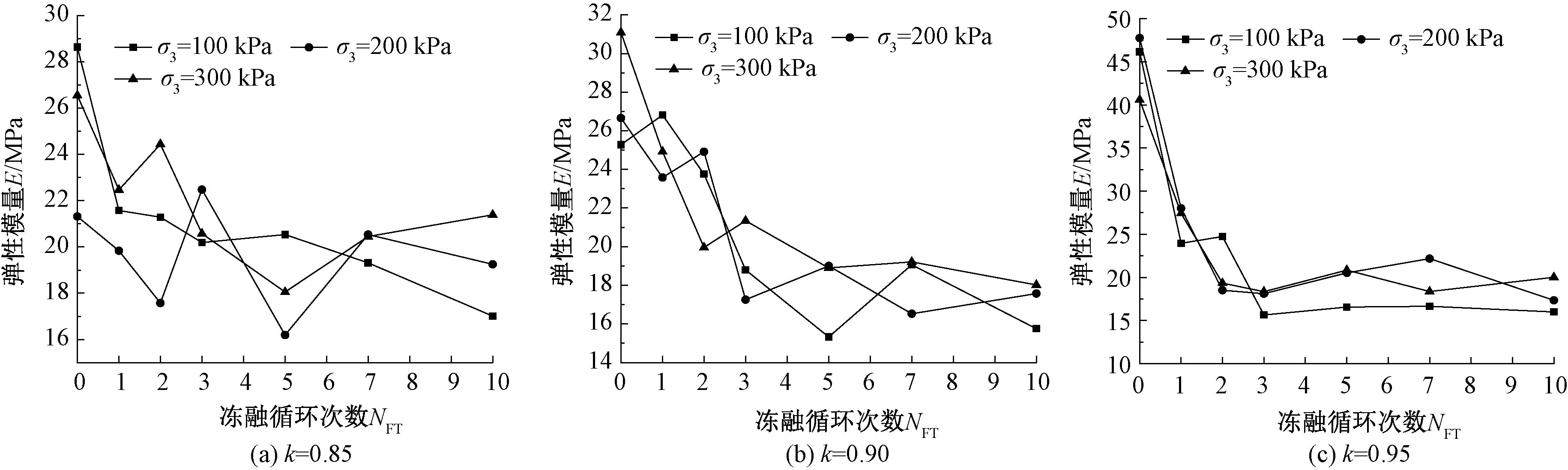
圖4 不同壓實系數條件下膨脹土彈性模量隨凍融次數與圍壓的發展規律

2.4 不同密實狀態膨脹土抗剪強度參數隨凍融循環的發展規律

2.4.1 黏聚力隨凍融次數的發展規律

具體步驟為:為盡量減少凍融過程膨脹土試樣表層水分蒸發量,利用塑料保鮮膜將預制好的膨脹土三軸試樣包裹起來并編號,凍融作用在凍融循環實驗箱(溫控精度:±0.5 ℃)的中進行試;將實驗箱溫度調至-15 ℃后運行10 min,確保箱內環境溫度達到均衡,放入膨脹土三軸試樣開始凍結作用,期間間隔20 min快速測量一次試樣軸向與徑向尺寸直至達到變形穩定標準,且總凍結時間不少于8 h;凍結過程結束后調整實驗箱溫度至20 ℃開始融化過程,試樣變形測量頻率同凍結過程直至達到穩定標準,且總融化時間不少于8 h。

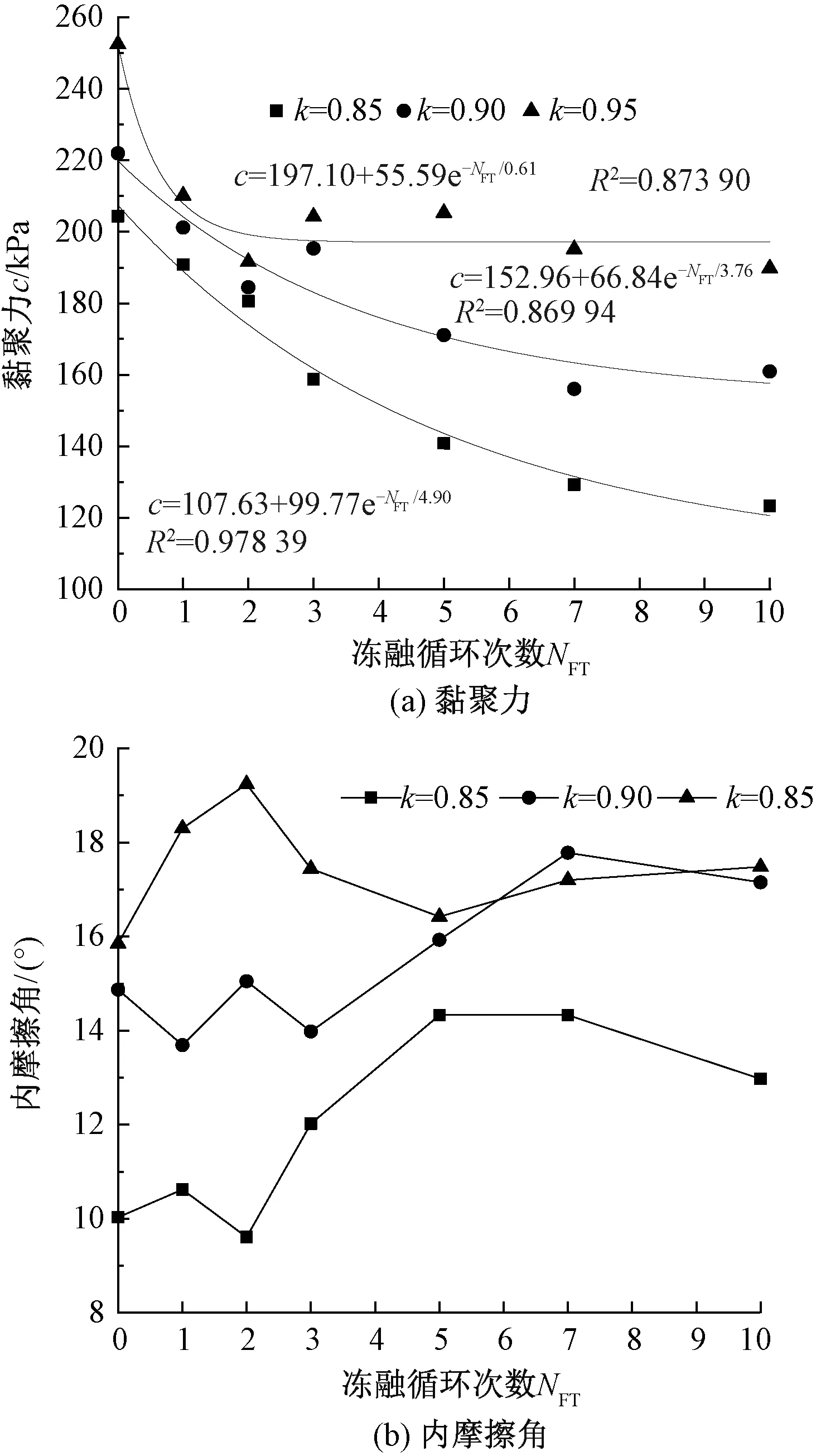
圖5 不同密實狀態膨脹土抗剪強度參數隨凍融次數發展規律

c=D+Ee-NFT/F

( 2 )

式中:D、E、F為通過試驗得到的參數。

經過同樣次數凍融作用后的膨脹土黏聚力c隨初始壓實系數k增加而增大;同一壓實狀態試驗組膨脹土黏聚力隨凍融次數增加而快速衰減,但衰減幅度逐漸次縮小;黏聚力快速衰減階段主要集中在前2次凍融循環,且衰減幅度隨著壓實系數的增大而逐漸增大,分別為未凍融狀態的88.4%(k=0.85)、83.1%(k=0.90)、75.8%(k=0.95),凍融循環作用下膨脹土黏聚力總體上呈指數型小幅波動衰減趨勢;經過10次凍融循環后膨脹土的黏聚力進一步衰減為未凍融狀態的60.3%(k=0.85)、72.5%(k=0.90)、75.2%(k=0.95)。

2.4.2 內摩擦角隨凍融次數的發展規律

2)凍融變形穩定標準與具體步驟。依據TB 10102—2010《鐵路工程土工試驗規程》[22]的規定,試樣2 h內變形量小于0.05 mm視為變形穩定,為提高試驗精度,本次采用的試樣變形凍融穩定標準為每2 h不大于0.01 mm,共進行10次凍融循環。

3 周期性凍融作用下膨脹土統一應力-應變關系

實施最嚴格水資源管理，落實三條紅線，須大力發展水利科學技術，切實提高水生產力。目前，我國許多地區還處在水生產力的人工和機械化階段，電氣及信息化的生產力水平非常有限，這是阻礙最嚴格水資源管理制度進一步落實的主要問題。因此，大力發展水利科學技術，汲取國際水管理的先進經驗，提高監控水資源的技術與管理能力，提高水生產力，是當前進一步落實最嚴格水資源管理制度的關鍵任務。此外，深入闡述水生產力的內涵，從勞動者、生產工具及勞動對象等方面，建立水生產力的定量評價指標體系，評價流域社會水生產力的發展水平，提出水生產力提高的途徑，是下一步研究的主要思路。

( 3 )

( 4 )

式中:a為初始切線模量倒數;b為極限偏應力倒數。

由圖2可知,軸向應變小于0.74%時,基于曲線計算的初始切線模量離散性大,其原因應是應力-應變關系受到了試樣安裝、加載系統與試樣初始接觸調整等因素影響,為此,以軸向應變0.9%對應的應力-應變曲線點進行初始切線模量計算。

利用式( 4 )得到的不同圍壓、凍融循環次數下的a、b值見表3。經過對數據分析發現,a在沒有經過凍融作用時隨圍壓增大而線性減小,而在承受凍融循環作用后則隨圍壓增大而線性增大;b則凍融前后均隨圍壓增加線性遞減;相同圍壓條件下,在前5次凍融過程中a與凍融次數呈線性增長關系,此后a與凍融次數的規律性較差。基于表3分別對a、b與凍融次數、圍壓關系曲線進行擬合,結果見圖6,則氣候邊緣地帶平頂山地區膨脹土Konder雙曲線模型參數分別為

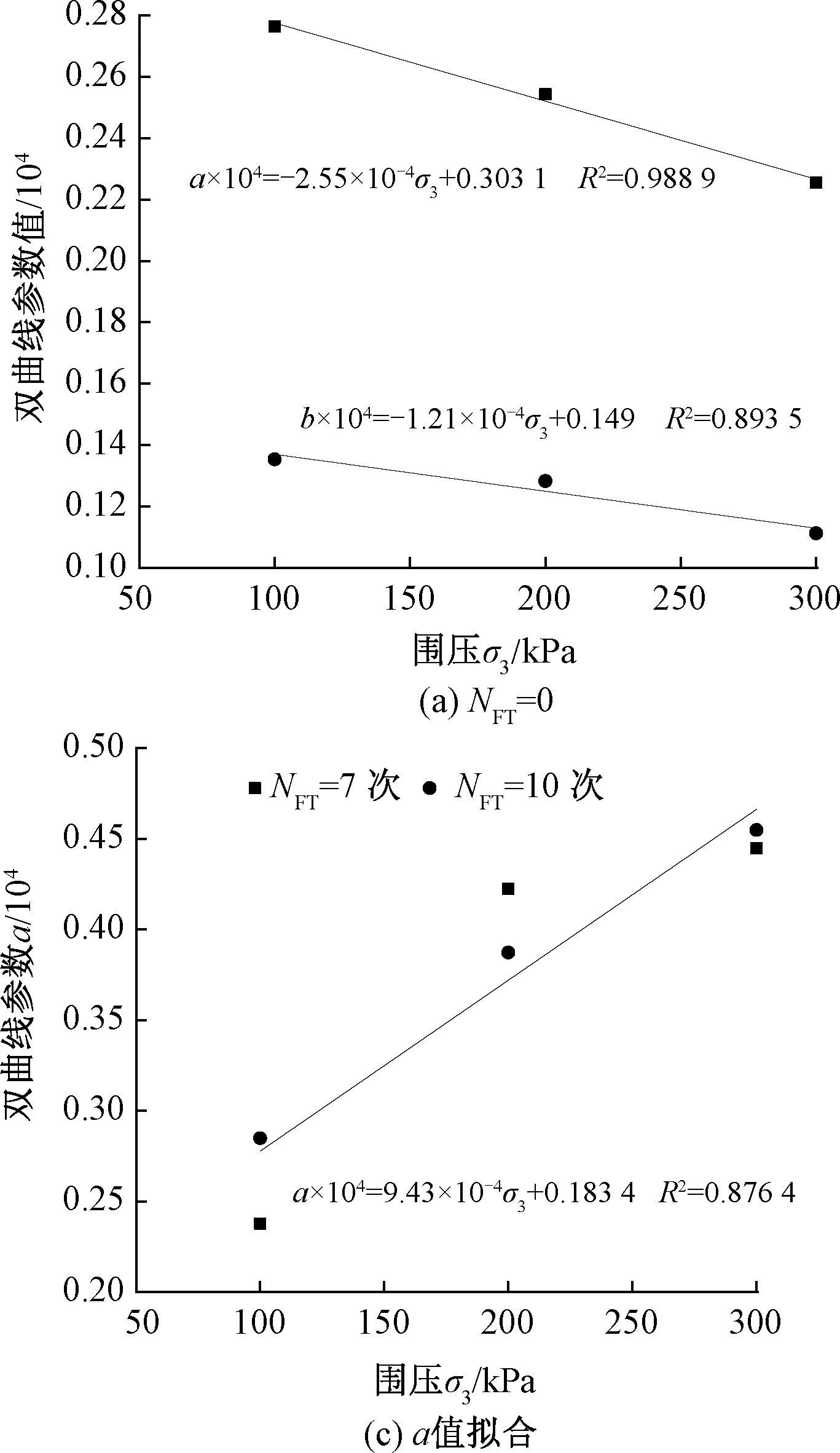
圖6 雙曲線參數擬合

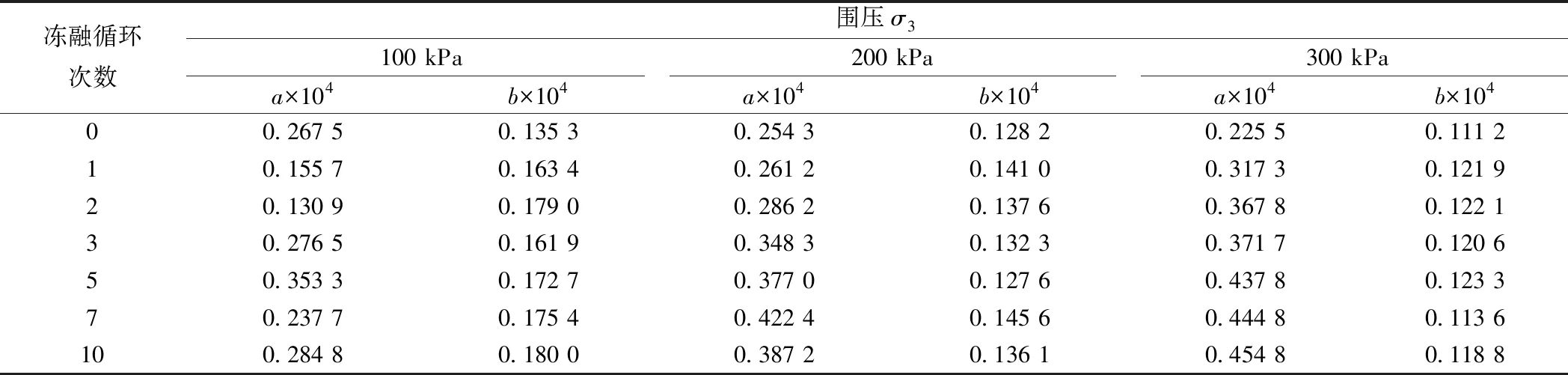
表3 不同凍融循環次數下的參數a、b值

a×104=

( 5 )

( 6 )

4 結論

1)密實狀態不變時,膨脹土相同軸向應變對應的主應力差值隨凍融次數增加而逐漸減小,應力衰減幅度隨凍融作用而逐次降低,且逐次衰減幅度與初始壓實系數關系不顯著。

2)膨脹土破壞強度、黏聚力與凍融次數之間為負相關關系,而與初始壓實系數則為正相關關系,凍融作用下膨脹土彈性模量總體上呈指數型衰減趨勢,內摩擦角波動性較大但總體隨凍融次數小幅增大。

男生甲 （生氣）別以為我們都是白癡，沒談過戀愛！成天茉莉茉莉，飛機上人家跟你說聲對不起，就以為人家看上你，呸，自戀！

3)凍融循環主要對初始切線模量具有顯著影響,而極限偏應力影響不顯著,且在第5次凍融循環后土體應力-應變關系趨于統一。