基于多目標并行加點映射代理模型的高速鐵路橋上行車安全快速評價方法

勾紅葉，梁 浩，趙 虎，肖 暢，劉 鈺

(1.西南交通大學 土木工程學院，四川 成都 610031；2.西南交通大學 橋梁智能與綠色建造全國重點實驗室，四川 成都 611756；3.中國鐵道學會 標準與認證部，北京 100844)

我國高速鐵路運營里程已達4萬 km,橋梁平均占比58%。軟土、高溫及凍脹等特殊地質與復雜氣候條件下的線路里程越來越長,線下基礎結構變形和層間結構性能劣化現象日趨突出[1-2]。針對高速鐵路橋梁,更應關注運行列車的安全性和舒適度[3-5]。

針對長期服役條件下高鐵橋上行車安全性問題,國內外學者已開展大量研究。黎國清等[6]根據橋梁徐變上拱引起的軌面高低不平順變化規律,利用有限元方法得出梁體徐變上拱狀態下列車安全運營的允許時速。蔣麗忠等[7]推導連續梁橋橫向變形與軌面狀態的映射關系,分析不同結構變形下列車運行的安全隱患。劉丹等[8]利用軌道板脫空的無砟軌道實尺模型,評估板端脫空長度對列車-軌道系統動力性能的影響。吳楠等[9]建立考慮橋梁基礎變形的車-軌-橋有限元模型,研究橋墩不同變形模式對行車安全評價的影響。Chen等[10]基于推導的多墩沉降與列車動態特性的映射關系,提出保障列車安全運營的橋墩沉降限值。Jin等[11]建立用于評價變形橋上列車運行安全性的簡化仿真模型,提高了行車安全的評估效率。文獻[12-13]刻畫了典型橋梁變形模式、不同車速和運行方式對高速列車時頻域動力性能的映射影響機制,揭示橋梁變形與行車安全的定量映射關系,制定了橋墩沉降、墩頂側偏、梁端轉角和徐變上拱的合理評價指標及剛度標準。然而,由于基礎結構性能演變是個復雜的非線性問題,如果將各種附加變形、層間聯結失效等非線性因素直接考慮至車輛-基礎結構系統動力學中,將引發巨大的計算規模,難以實時快速評價復雜環境下橋上行車安全。因此,有必要提出一種求解計算量小、有物理機制解釋,亦能高精度計算橋上列車動力響應特征的理論方法,為復雜服役條件下行車安全快速評價及預判提供理論基礎。

針對動力分析數值模擬耗時長、成本高等問題,不少學者基于代理模型技術,通過模擬輸入與輸出的映射關系,高效預測真實系統的復雜響應。常用的代理模型有多項式響應面(RSM)[14]、徑向基函數(RBFs)[15]、克里金模型(Kriging)[16]、神經網絡(NN)[17]等。其中,Kriging模型可同時對響應均值與方差進行預測,具備強大的序列優化設計潛力與多維非線性自適應擬合功能,已被廣泛用于結構優化、可靠度分析、模型近似等領域。Feng等[18]基于Kriging模型,通過分解EI準則提出一種基于高效全局優化算法(EGO)的多目標優化方法,提高了設計優化的計算效率與精度。Echard等[19]提出了一種基于Kriging模型與蒙特卡洛模擬的可靠度分析方法,顯著降低了分析過程中數值模型的調用次數。李永樂等[20]利用Kriging模型建立了無砟軌道簡化模型與精細模型的映射關系,提出了無砟軌道簡化模擬方法,改善了無砟軌道仿真計算復雜、低效等問題。然而,上述研究成果主要基于真實系統特定響應的預測尋優,難以精確描述系統全局趨勢的變化規律。

有鑒于此,本文提出并驗證了一種針對Kriging代理模型的多目標并行加點新算法,該算法可同時考慮系統全局搜索與局部開發;并以軟土沉降區域運營高鐵為例,通過將車-軌-橋耦合振動模型與優化算法相結合,訓練板底脫空條件下橋墩沉降與列車動力響應的多點映射關系,建立復雜服役條件下高效率計算行車安全參數的映射代理模型,進而實現橋上行車安全性的快速精準評價。

1 基于Kriging代理模型的多目標并行加點算法

1.1 Kriging代理模型

通過某高斯靜態隨機過程,Kriging模型[16]可實現變量與響應的一一映射。該隨機過程由線性回歸模型與隨機狀態模型兩部分組成,即

( 1 )

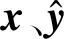
( 2 )

其中,xi、xj為自變量x中不同類型的設計變量;R(xi,xj)為xi、xj的空間相關函數,以高斯相關函數應用最為廣泛,其表達式為

( 3 )

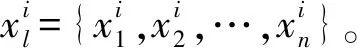
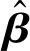
( 4 )

( 5 )

式中:F、R分別為變量樣本對應回歸函數值、相關函數值構成的矩陣;Y為變量對應真實響應構成的矩陣;N為樣本變量個數。

( 6 )

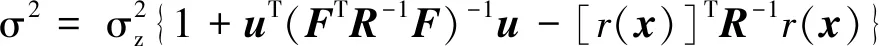
( 7 )

式中:r(x)為未知變量與樣本變量之間的相關函數向量;u=FTR-1r(x)-f。

1.2 多目標并行加點算法

受抽樣數目、分布等影響,基于初始樣本建立的Kriging代理模型往往無法反映真實系統的映射機理,常需設計序列優化算法對模型進行優化更新,不斷提高響應預測精度。

序列優化是指代理模型基于一定的加點準則,通過自適應的順序添加新樣本點,不斷更新優化、直至收斂的過程。其中,加點準則直接關系到新樣本的形成,并對模型的優化效率、最終精度等產生重要影響。因此,對于復雜車-軌-橋系統的響應預測,研究和發展高性能的加點策略尤為關鍵。

1.2.1 優化目標分析

要保障高鐵基礎結構性能演變下運行列車的優良工作狀態,實現信息更新條件下的橋上行車安全快速準確評價與預測,則要求基于代理模型構建的映射關系不僅能夠準確反映性能劣化對列車動力響應的影響機制,更要確保列車動力性能閾值輪廓的超高精度刻畫,這是判斷行車安全舒適性的核心與關鍵。鑒于此,提出一種新的序列優化方法,使代理模型同時滿足系統全局變化趨勢模擬與特定區間超高精度預測的優化目標。

1.2.2 并行加點準則

基于上述優化目標,本節提出一種多目標并行加點準則,該準則在一次序列優化過程中同時對整體與局部進行優化加點。

1)全局加點過程

均方差準則方法(MSE)是一種基于響應預測的均方差最大值進行加點的優化策略[21]。其將預測不確定性較大的點作為更新樣本,避免了局部重復加點,可快速揭示系統響應全局趨勢。本節采用該準則進行全局加點,即通過智能算法求解如下優化問題。

( 8 )

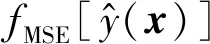
然而,由于車-軌-橋系統的強非線性特征,作為空間填充性質的加點策略,僅采用全局加點的均方差準則常常收斂較慢,難以滿足閾值區域的高精度預測要求。

2)局部加點過程

局部加點的目的是搜索設計空間中閾值的潛在區域,并對其預測精度進行優化提高。行車安全閾值作為指定的具體數值,采用針對全局最大/最小值進行優化的EGO方法[22]往往難以實現。為解決這一問題,Bichon等[23]基于EGO,通過輪廓估計思想,發展出高效全局可靠度分析方法(EGRA),大大推動了可靠度領域的發展。

在可靠度分析過程中,EGRA方法[23]根據服從正態分布的高斯隨機過程,搜索比當前極限狀態更優或不確定性更大的樣本點,通過不斷明確極限狀態輪廓(即閾值輪廓),最終實現失效概率的高精度預測。其實質是對指定響應數值對應的輸入變量進行預測、優化。鑒于此,本節引入EGRA方法,將其應用于特定區間優化的局部加點過程中。

( 9 )

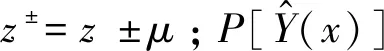
預期函數的積分解析形式表示為

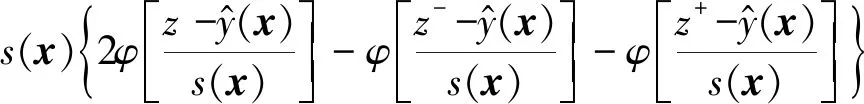
(10)

式中:Φ(·)、φ(·)分別為標準正態累積分布函數與標準正態概率密度函數;μ正比于s(x),通常記為μ=2s(x)。

在此基礎上,通過求解fEF(x)最大值對應的樣本點即可實現對代理模型的優化更新,其表達式為

xnew=argmax{fEF(x)}

(11)

1.2.3 EF-MSE算法的提出和實現

基于上述并行加點準則,本節提出一種基于fEF與fMSE兩種優化函數并行加點的優化算法(EF-MSE)。該算法可同時實現整體趨勢模擬與局部高精度預測,基本優化流程見圖1。

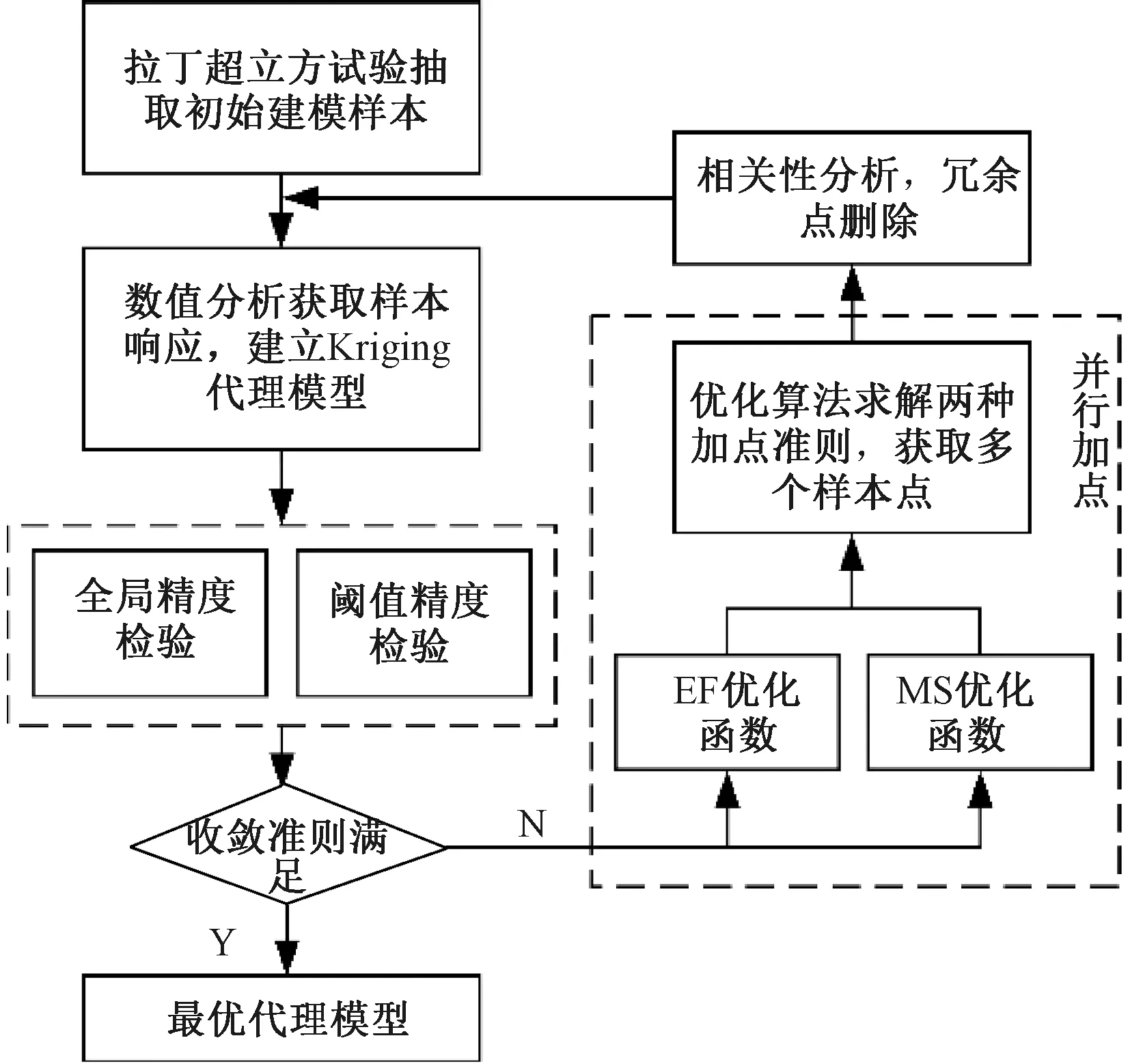
圖1 EF-MSE多目標并行加點流程

具體步驟如下:

Step1在給定設計空間中生成建模所需的初始樣本變量。采用可使樣本隨機布滿整個設計空間的拉丁超立方試驗設計方法[24]進行抽樣。

Step2通過數值分析等物理方法獲取現有樣本變量的實際響應,并針對相應樣本對構建Kriging代理模型。

Step3分別計算當前Kriging模型全局趨勢、閾值區域預測與實際響應的偏差情況。

Step4檢驗Kriging模型是否收斂。若已滿足設定的收斂條件,則可停止迭代,當前模型即輸出為最優代理模型;否則,需執行Step5,繼續優化更新。

Step5通過智能優化算法求解基于fEF函數與fMSE函數的兩種加點準則,同時得到多個并行的新樣本。優化算法采用全局尋優強、搜索效率高的遺傳算法[25]。

Step6利用高斯準則進行新樣本之間、新樣本與現有樣本之間的相關性分析,刪除冗余樣本,得到最終優化樣本。高斯函數見式( 3 ),將相關性大于0.9的樣本視為冗余樣本。

Step7將優化樣本加入現有樣本變量,轉至Step2,從而不斷更新Kriging代理模型,直至收斂。

本節提出的序列優化算法結合fEF與fMSE兩種性能互補的優化函數,形成多目標并行加點的優化策略,可在快速搜索全局最優值的同時有效提高模型整體精度,具備充分的理論可行性和優越性。

2 EF-MSE算法性能分析

以某一維函數為研究對象,通過對比EF-MSE算法下不同優化目標的收斂情況,驗證所提算法的可行性;基于實際研究需求,將不同優化算法應用至高維復雜非線性函數中,分析EF-MSE算法在全局精度及閾值搜索方面的優越性。

2.1 可行性驗證

以實現函數全局精度優化及閾值搜索為目標,選取一維函數的Kriging模型分別對EGRA、MSE及EF-MSE優化方法進行了比較。其中,閾值定義為函數零點。該一維函數[26]曲線見圖2,其表達式為

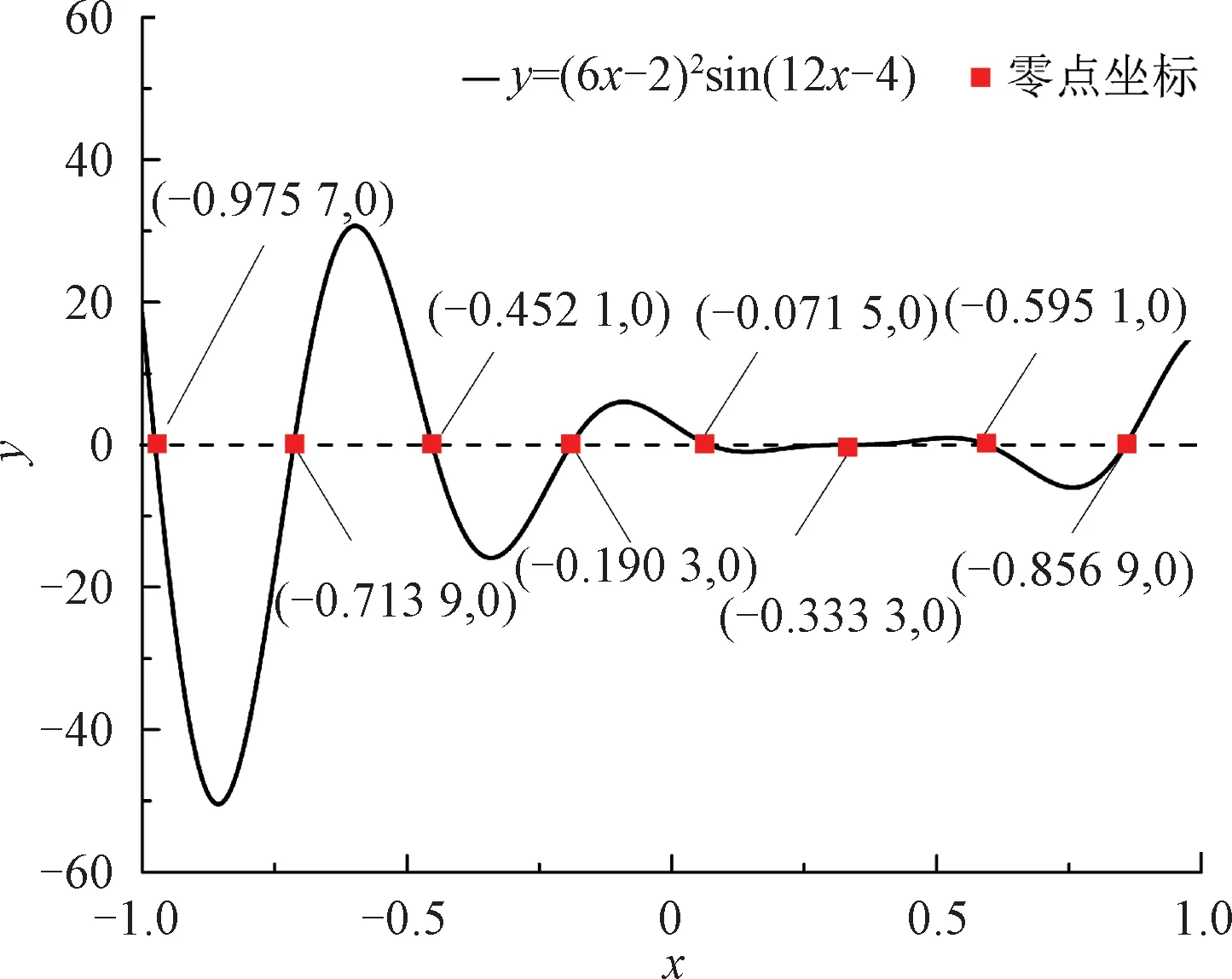
圖2 一維函數圖像

y=(6x-2)2sin(12x-4)x∈[-1,1]

(12)

由圖2可知,該函數存在5個局部峰值,并有8個函數零點,是典型的非線性多峰一維函數。

為方便比較,應用Matlab中的DACE程序[27]建立基于相同初始樣本與優化次數的Kriging代理模型,試驗初始樣本選取均布設計空間的5個變量。基于不同加點準則優化算法循環4次與8次后的擬合曲線見圖3。各準則針對不同優化目標的精度比較見表1。表1中,精度通過相關點位實際響應與預測響應的平均絕對誤差表示,其中全局精度采用20個均布樣本點進行計算。

表1 優化結果對比

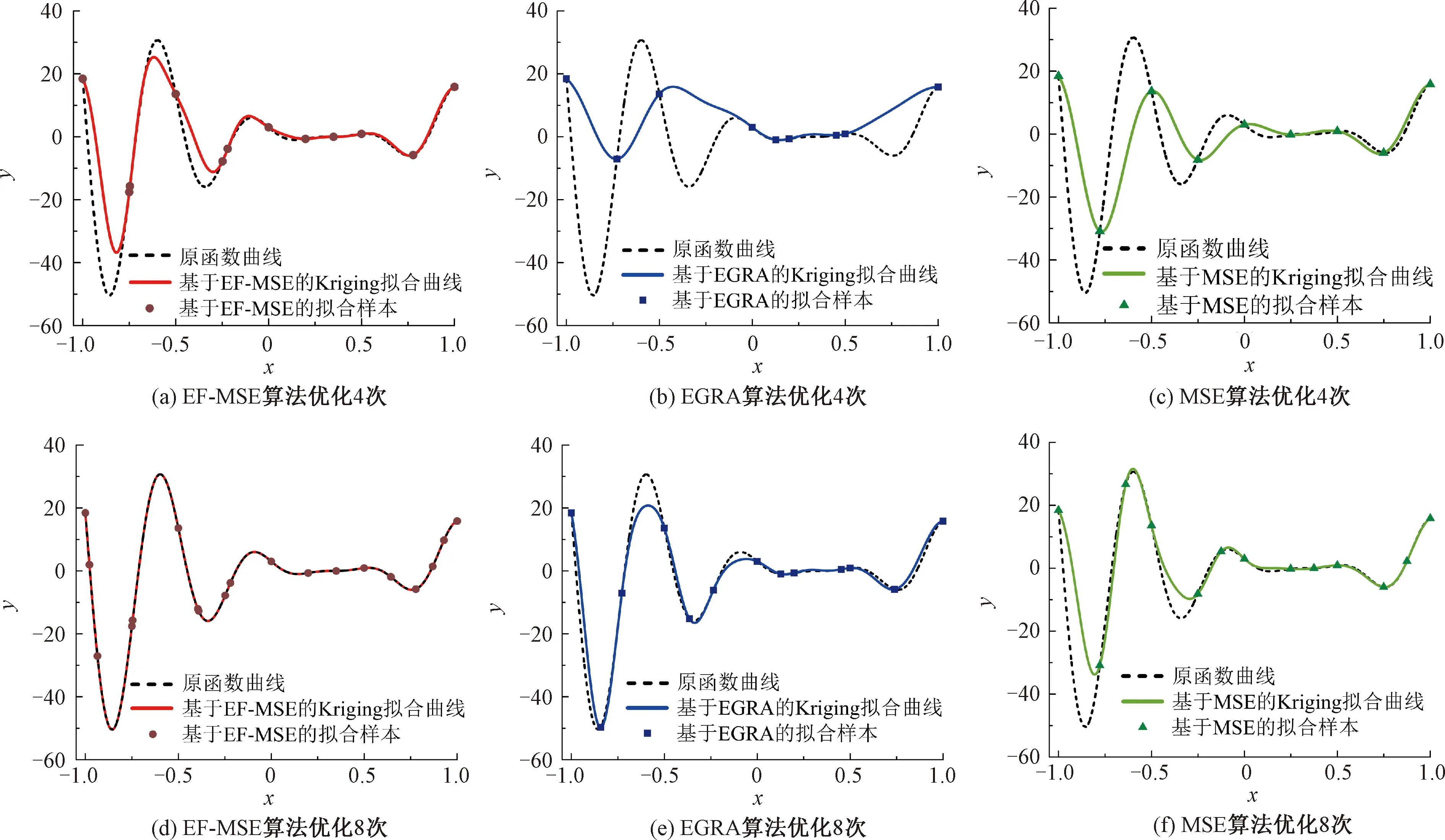
圖3 基于不同優化算法的Kriging擬合曲線

由圖3可知,EGRA算法加點存在徘徊現象,在早期優化過程中更偏向局部收斂;MSE算法及EF-MSE算法的優化樣本離散性相對較好,EF-MSE算法優化結果與原函數曲線擬合程度最高。由表1可知,在相同初始樣本與優化次數的情況下,采用EF-MSE優化算法在全局趨勢預測、零點搜索方面相比EGRA、MSE算法均有顯著提高,這表明提出的優化算法可較好地兼顧系統全局響應預測及特定區間尋優,具備多目標優化的可行性。

2.2 復雜非線性函數優化性能對比

本節以兩種典型的復雜二維非線性函數為例,對比分析了EF-MSE算法在全局趨勢與閾值搜索方面的優越性。兩函數閾值均定義為函數零點。

兩個函數的等值線見圖4。函數1[23]為二維非線性多模態函數,多個局部極值點集中分布于該函數給定的設計空間內,零點等值線具有極強的非線性。函數2[28]為二維非線性立方函數,該函數等值線分布相對較為規律,但變化坡度極大,常數項的存在決定了其零點等值線的高度非線性。

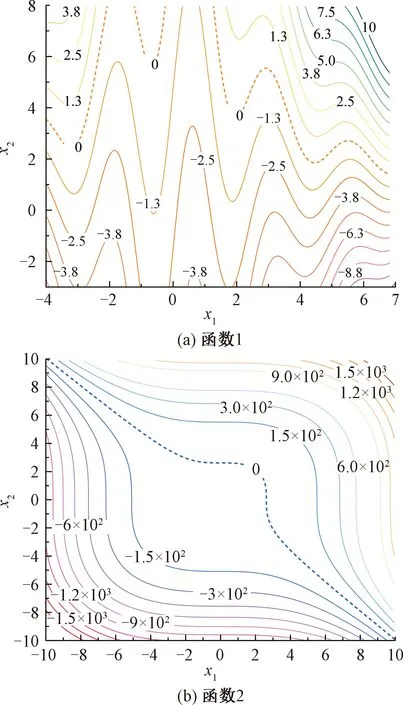
圖4 典型非線性二維函數等值線

函數1表達式為

(13)

函數2表達式為

(14)

不同優化算法的收斂準則分別定義為

MSE優化算法為

(15)

EGRA優化算法為

max{fEF(x)}≤εef

(16)

EF-MSE優化算法為

(17)

當上述算法中的優化函數值小于或等于式(15)～式(17)右邊設定的閾值時,算法即視為收斂,可停止計算。需要注意由于EF-MSE算法實質為并行加點過程,因此收斂準則中各優化函數滿足收斂要求時僅結束自身優化進程,并不終止算法總體優化進程。

為正確分析EF-MSE并行加點算法對于相應單一加點算法的性能狀態,不同算法中相同優化函數的收斂條件應保持一致,相關參數設置見表2。

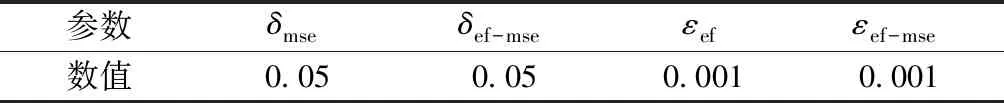
表2 參數設置

基于20個初始樣本,采用不同算法對上述函數全局及閾值預測精度的優化過程見圖5、圖6(全局與閾值預測精度分別通過均布設計空間與零點等值線的20個檢驗樣本真實值與預測值的平均絕對誤差進行計算)。

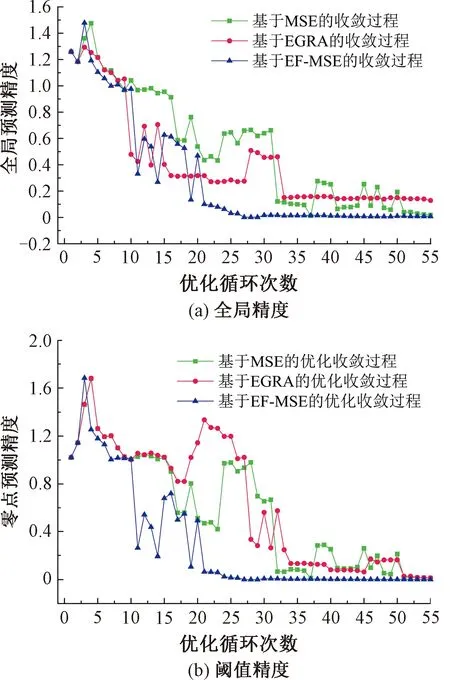
圖5 二維非線性多模態函數優化過程

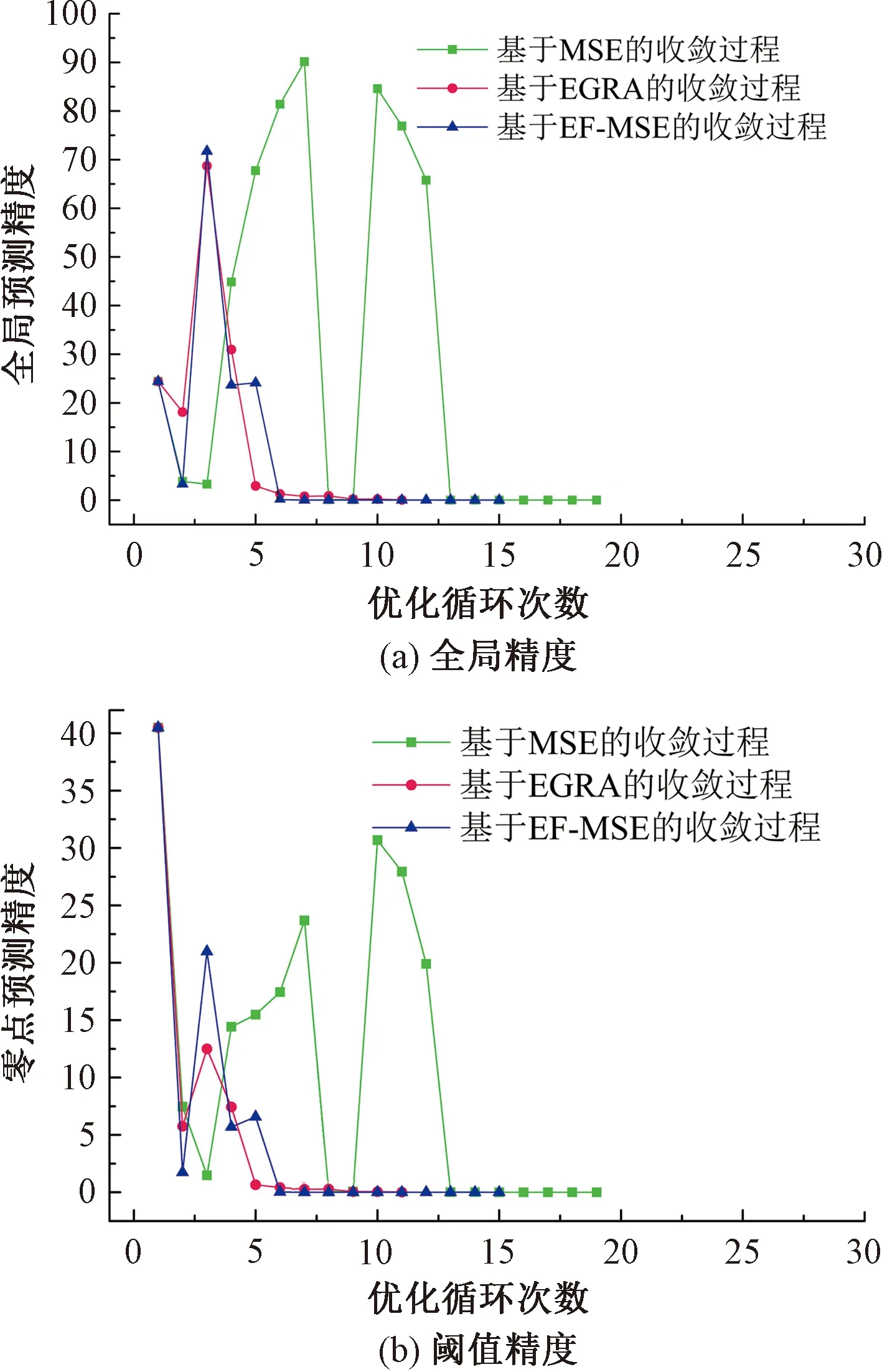
圖6 二維非線性立方函數預測精度優化過程

由圖5、圖6可知,EGRA算法雖能較快收斂,但全局預測精度相對較低;MSE算法收斂時全局及閾值預測精度基本一致,但優化次數相對較多,優化中后期預測精度仍有較大波動,穩定性相對較低;相比之下,EF-MSE算法能夠有效結合MSE算法與EGRA算法各自的優勢,以更少的迭代次數迅速收斂至更為精確的預測結果。

為進一步分析不同優化算法在優化收斂時的預測精度、計算成本及優化效率,對于不同測試函數各優化算法收斂時的優化結果見表3。為避免偶然性,表中數據為50次序列優化結果的平均值。

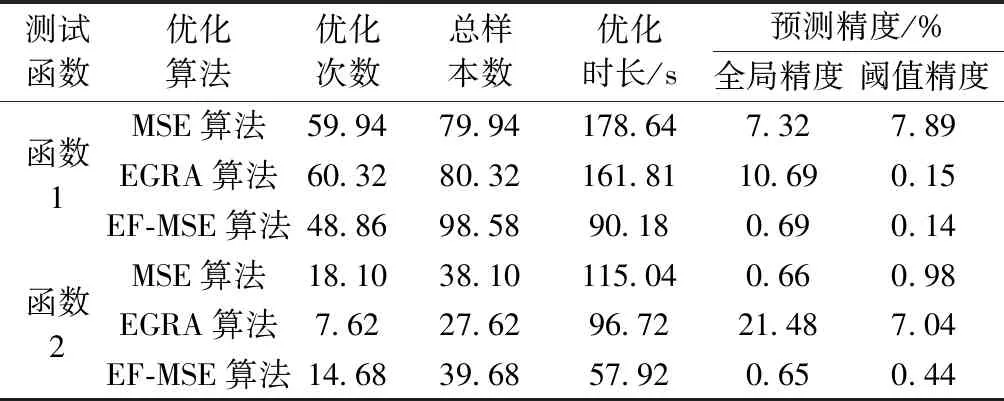
表3 不同優化算法收斂結果對比

由表3可知,采用EF-MSE算法優化能夠在保持良好預測精度的同時有效減少優化次數,相應地,雖然EGRA算法對于空間分布較為規律的立方函數僅需7.62次優化,但過早的收斂及較大的函數坡度也導致了較差的預測結果。作為并機計算的優化算法,EF-MSE算法程序運行總時長相比其他算法大大縮短,優化效率顯著提高;此外,在同一優化函數收斂條件相同的情況下,雖然EF-MSE算法在一次優化過程加入的樣本是其他算法的兩倍,但總樣本數僅略大于其他算法,表明EF-MSE算法并不是兩種算法的簡單疊加,而是具備更加穩定和高效的優化性能。

3 高鐵橋上行車安全快速評價方法

基于前述Kriging模型多目標并行加點算法,本節提出了一種行車安全快速評價方法,并以軟土沉降區域運營高鐵為例,通過建立信息更新條件下高效率求解行車安全參數的映射關系代理模型,實現基于代理模型的橋上行車安全快速精準評價。

3.1 快速評價方法的提出

快速評價方法主要包括性能演變數據檢測監測、列車響應預測、快速評價與預警3個模塊,見圖7。檢測監測模塊主要記錄高鐵沿線橋梁-軌道結構服役狀態,列車響應預測模塊通過將實測數據輸入映射關系代理模型,實時輸出車輛響應數值及變化趨勢,進而實現對橋上行車安全性的快速精準評價和預警。其中,映射代理模型可反映不同基礎結構服役性能演變(橋墩沉降、梁端轉角、離縫、板底脫空、上拱等)與列車動力響應的多點映射關系,是實現快速精準評價的核心基礎。

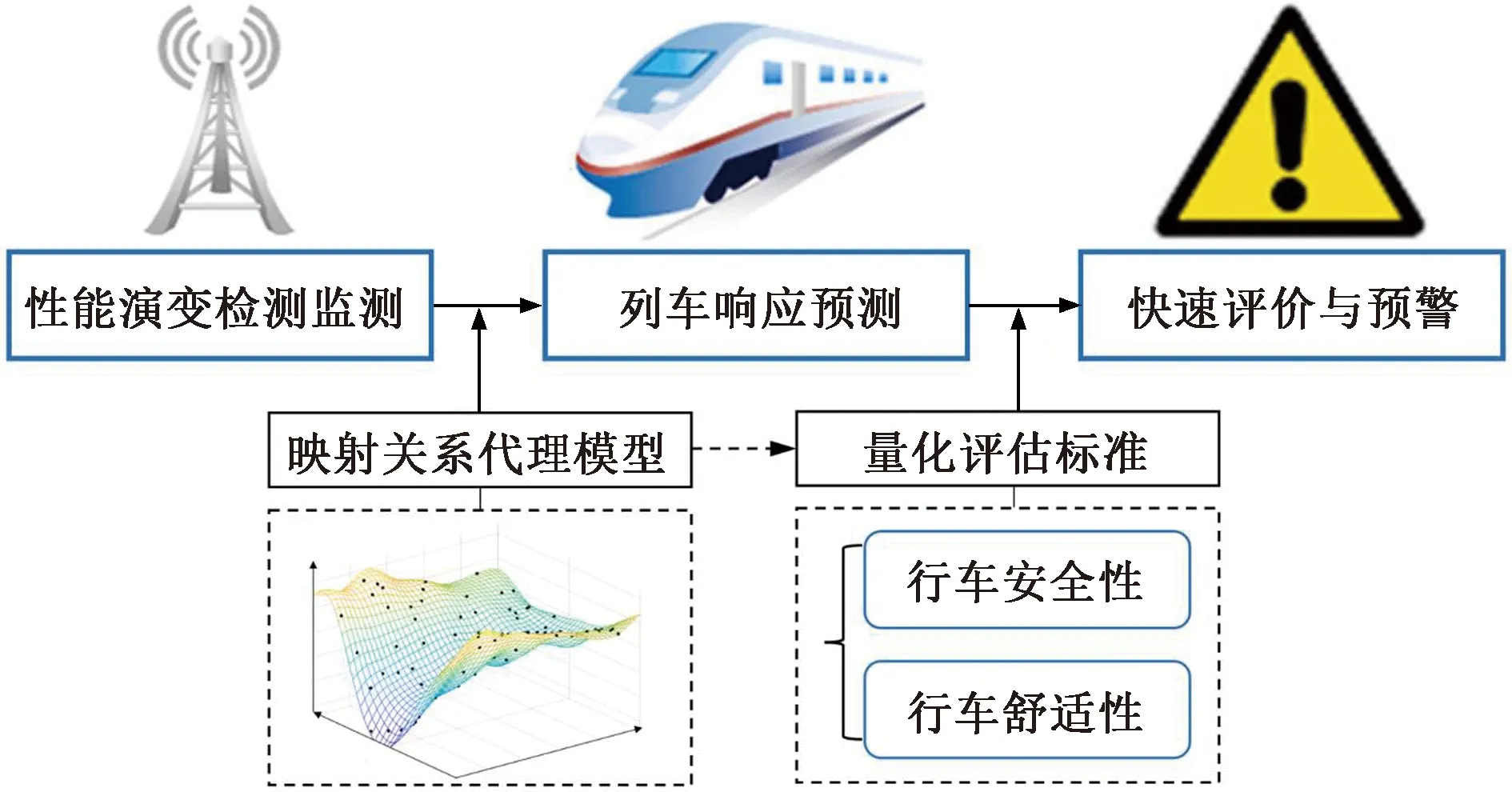
圖7 行車安全快速評價方法

3.2 多點映射關系

已有研究表明,軟土地質區域高鐵橋梁基礎不均勻沉降現象突出[29]。加之軌道結構產生的板底脫空、離縫、上拱等病害現象[30],保障橋上行車安全面臨重大挑戰[31]。

鑒于此,本節對我國軟土地區某高鐵區段線下結構監測結果進行分析,以探明軟土地區高鐵橋梁基礎結構典型病害特征及其對列車動力性能的影響規律。在此基礎上,分析不同性能演變與列車響應的預測需求,進而闡明代理模型所需構建的多點映射關系。2016年11月9日某高鐵上行段(K1308+733.919—K1309+159.713 75)基礎結構性能演變實測數據見表4。表4中,板底脫空均為軌道板底縱向脫空,對應橋墩墩頂位置處。

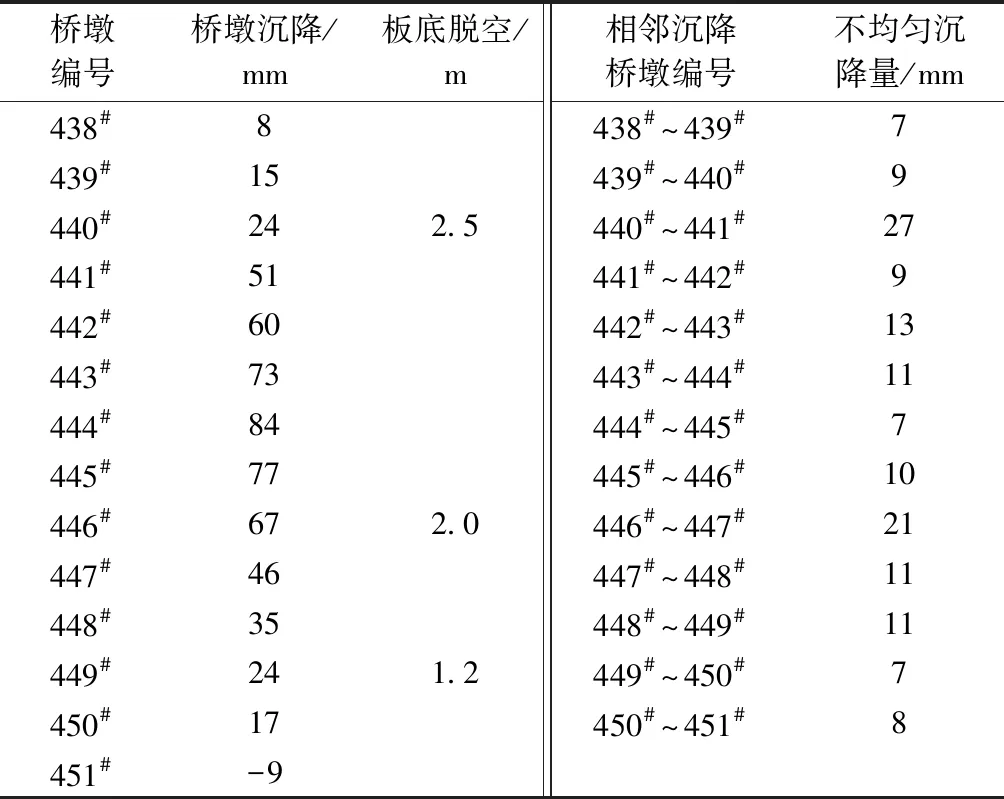
表4 軟土地區某高鐵基礎結構性能演變實測數據

從表4可知,監測區段線下基礎均發生不同程度沉降,相鄰墩不均勻沉降差最大達27 mm,橋梁發生附加變形的同時,部分軌道板底部出現沿縱向的脫空現象,并主要集中于沉降墩附近。

以高速鐵路32 m簡支箱梁橋和CRTS Ⅱ型板式無砟軌道以及CRH2列車為研究對象,針對橋墩沉降和底座板脫空這一典型工況,基于文獻[12]研發的橋梁-軌道變形映射模型,求解軌道附加不平順并作為系統激勵輸入至車-軌-橋耦合振動模型[13]中,獲得典型工況下列車動力響應。

速度為350 km/h列車的動力響應見圖8。由圖8可知,由于橋墩沉降與板底脫空僅引起軌道發生豎向變形,列車經過沉降與脫空區域時,車體豎向加速度與輪軌垂向力發生顯著變化,而橫向加速度與輪軌橫向力基本未發生變化,表明橋墩沉降與軌道板脫空組合作用主要影響車-軌-橋系統的豎向振動,而對橫向動力性能影響較小。

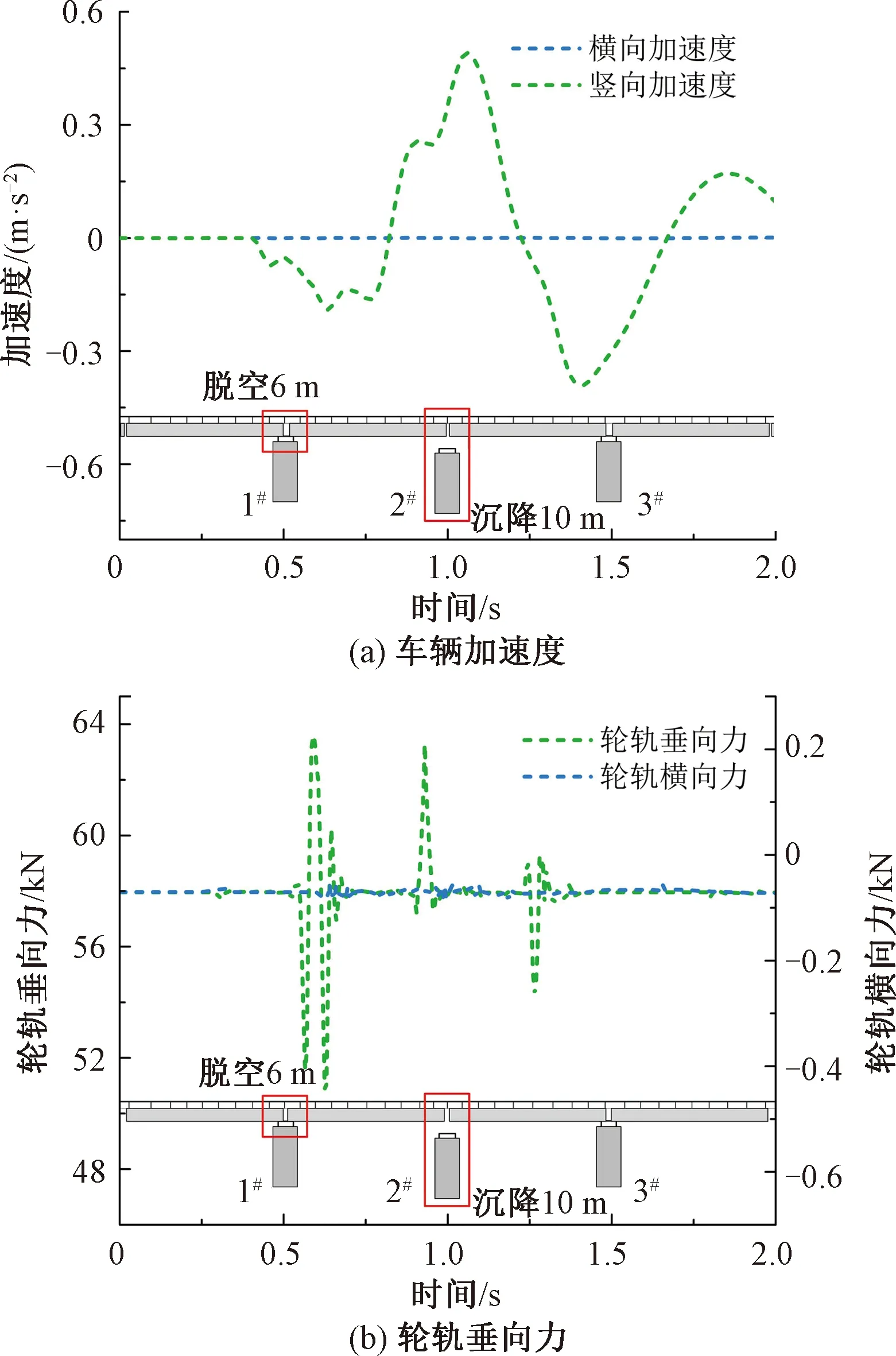
圖8 橋墩沉降與板底脫空組合工況下列車動力響應

測量和計算結果表明,軟土地區高速鐵路基礎結構典型病害為橋墩不均勻沉降與軌道板底脫空,并對列車豎向動力性能產生明顯影響。此外,橋梁豎向變形作用下,列車動力響應隨車速提高不斷增大[13]。因此,綜合考慮沉降區域運營高鐵行車安全性與舒適性,以行車速度350 km/h為計算工況,映射關系考慮沉降與脫空組合作用,對應其引起的列車輪軌垂向力與豎向加速度變化。其中,輪軌垂向力與豎向加速度變化閾值基于輪重減載率與豎向加速度的定義[13]及TB 10621—2014《高速鐵路設計規范》[32]規范限值進行計算,分別為10.376 kN、0.972 m/s2;沉降與脫空范圍分別為0～30 mm、0～6 m,脫空位置選擇對軌道變形更為不利的沉降相鄰墩處[13]。

3.3 映射關系代理模型的構建與檢驗

基于圖1所示EF-MSE算法的代理模型優化流程,構建板底脫空條件下橋墩沉降與輪軌垂向力變化量的映射關系代理模型。

首先采用拉丁超立方抽樣選取20個不同橋墩沉降與板底脫空的組合工況,通過車-軌-橋耦合振動模型,獲取相應的列車輪軌垂向力變化量,形成初始樣本對,從而建立初始Kriging代理模型;其次根據結合fEF函數與fMSE函數的并行加點準則,對動力響應整體變化趨勢與安全限值區域進行迭代優化,直至滿足優化收斂要求,最終完成映射關系代理模型的構建。其中,模型整體精度基于均布設計空間的20個樣本對,通過計算其響應預測結果與車軌橋有限元仿真結果的平均誤差進行檢驗。而對于閾值輪廓的刻畫精度,則通過對當前代理模型模擬的閾值等值線均勻抽取的20樣本對,計算其數值模擬結果與閾值的偏差進行檢驗。本節將全局預測平均絕對誤差小于5%、閾值預測偏差小于1%作為精度收斂條件。需要注意,由于列車運行過程中輪軌垂向力連續變化,這里僅考慮對行車安全最不利的最大減少量[13]。

精度檢驗結果顯示,對于整個設計空間,代理映射模型預測輪軌垂向力變化量的平均絕對誤差為2.86%,而針對安全限值附近區域的預測偏差僅為0.81%,均滿足優化目標,表明基于EF-MSE算法優化的代理模型可較好地實現全局趨勢與閾值輪廓的預測需求。收斂后代理模型對于輪軌垂向力變化量的模擬結果見圖9。

由圖9可知,相較于橋墩沉降和板底脫空單獨作用,組合效應顯著加劇了輪軌垂向力的變化,對列車運行安全性更為不利。隨沉降量增大,輪軌垂向力近似呈線性增大,而板底脫空對輪軌垂向力的影響相對較小,僅在大范圍脫空時產生顯著影響,并隨橋墩沉降量的增大不斷減弱。

同理,基于EF-MSE優化算法,構建了板底脫空條件下橋墩沉降與豎向加速度最大變化量的映射關系。收斂后代理模型模擬的映射關系,對比數值模擬結果見圖10,模型整體預測的平均偏差為1.78%,而閾值區域預測偏差為0.18%,滿足收斂要求。

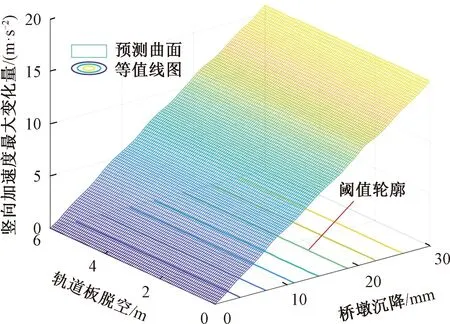
圖10 板底脫空條件下橋墩沉降與豎向加速度最大變化量的映射關系

由圖10可知,豎向加速度變化隨橋墩不斷沉降持續加大,而板底脫空對豎向加速度影響很小,僅造成豎向加速度的微小波動。

此外,對于梁端轉角、離縫、上拱等其他多種基礎結構性能劣化現象,可同樣基于上述代理模型技術,通過訓練映射關系,快速輸出對應工況下的行車動力響應,從而避免大規模的車-軌-橋耦合計算。由于篇幅有限,這里僅以軟土地區橋墩沉降與板底脫空兩種典型工況進行介紹。

3.4 基于代理模型的行車安全舒適性評價

采用基于代理模型的行車安全評價方法,通過構建的映射關系代替復雜耗時的車軌橋計算,實時準確輸出上述高鐵監測區段不同工況下的列車動力響應,見表5。

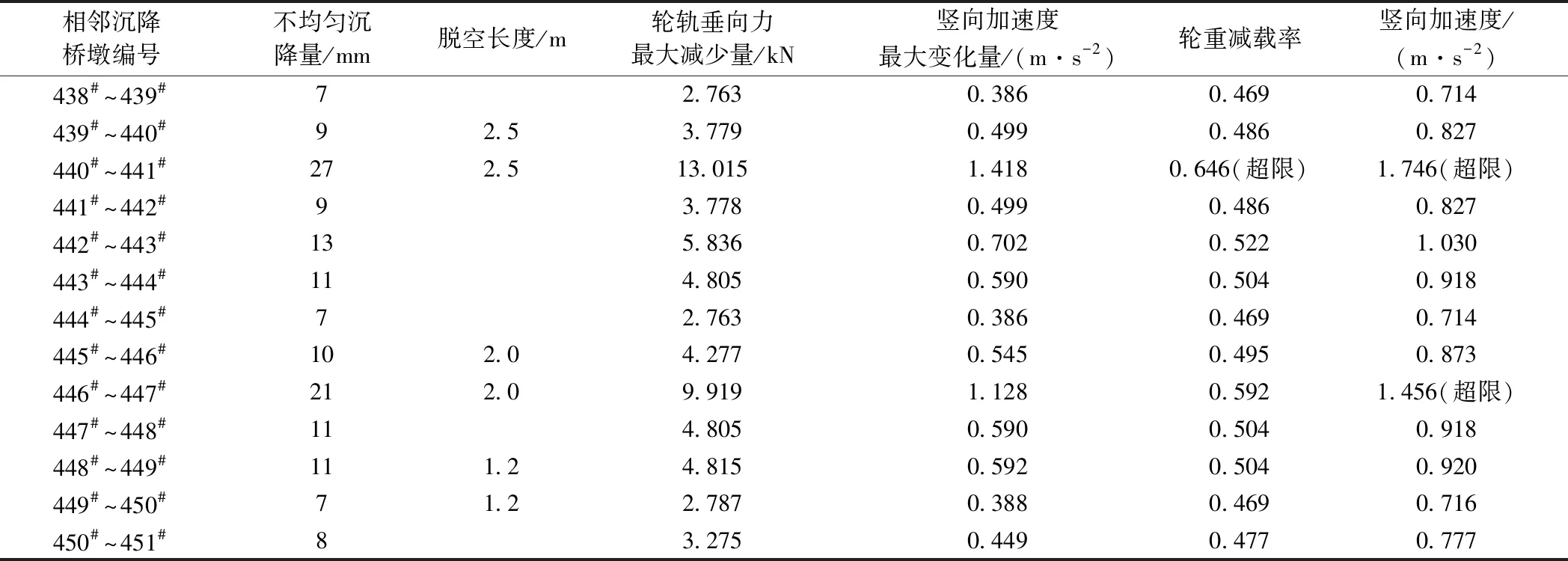
表5 基于映射代理模型求解列車動力響應

由表5可知,當列車由440#橋墩經過441#橋墩過程中,行車安全與舒適性超限,輪重減載率最大達0.646,最大豎向加速度為1.746 m/s2,此時不均勻沉降、板底脫空縱向長度分別為27 mm、2.5 m,對于即將通過該橋跨的列車,應及時發出降速預警,以確保列車安全與舒適性。由此可見,基于代理模型的行車安全評價方法實現了行車安全快速準確評價與預警,為保障列車長期運營安全提供了基礎。

4 結論

本文針對傳統方法難以快速評價列車安全舒適性的難題,提出了一種在序列優化迭代中兼顧全局搜索與局部開發的智能算法,訓練了不同橋梁附加變形及基礎結構服役性能演變與車輛動力響應的多點映射關系,建立了信息更新條件下高效率求解行車安全參數的代理模型,提出了基于代理模型的橋上行車安全評價方法。主要結論如下:

1)相較于傳統加點算法,提出的EF-MSE算法在序列優化迭代中可對全局搜索與局部開發同時優化,自適應地提高模型多目標優化精度,顯著減少加點次數,收斂速度大大提高,并表現出良好的穩定性。

2)建立的映射關系能夠正確反映基礎結構性能劣化對列車動力響應的影響規律,精準刻畫列車動力性能的閾值輪廓;代理模型求解計算量小、有物理機制解釋,亦能高精度、高效率計算橋上行車動力響應特征。

3)提出的基于代理模型的行車安全快速評價方法,可以用于復雜服役條件下行車安全性能的快速評價及預判,促進了高鐵橋上行車安全智能評價和預警系統的逐步形成,有力保障了橋梁-軌道體系的安全服役。

4)可進一步開展數據與代理模型、物理機制深度融合的橋上行車安全智能預測、評價及控制方法研究。