磁懸浮列車磁浮力的計算與分析

汪 斌，王偉旭，孫體佳，湯港歸

(西南交通大學 土木工程學院，四川 成都 610031)

自1842年英國物理學家Samuel Earnshaw提出磁懸浮概念以來,磁懸浮技術得以不斷發展。1922年,德國工程師Hermann Kemper提出電磁懸浮原理,于1934年申請了磁懸浮列車的專利,自此磁懸浮技術得以運用到交通運輸之中。磁懸浮列車(Maglev Train)是一種無接觸的地面有軌交通工具,利用磁吸力或磁斥力懸浮車輛,以直線電動機牽引列車,具有速度域寬、爬坡能力強、噪聲小、維修成本低、乘坐舒適和安全等特點[1]。此外,磁懸浮列車與軌道之間不存在直接接觸。相比于傳統機械式輪軌接觸系統,磁懸浮交通避免了輪軌摩擦帶來的損耗[2]。因此,磁懸浮列車作為未來的交通運輸方式受到世界各國的廣泛關注與青睞。磁懸浮列車懸浮模式可分為:電磁懸浮(Electromagnetic Suspension,EMS)、電動懸浮(Electrodynamic Suspension,EDS)、超導釘扎磁懸浮(SPL)[3]。其中電磁懸浮技術出現時間最早,對其進行研究的國家也較多,包括德國、中國、韓國等。電動懸浮技術分為低溫超導電動懸浮和永磁電動懸浮,對低溫超導電動懸浮技術的研究主要在日本,而對永磁電動懸浮技術的研究主要在美國、中國等國家。超導釘扎磁懸浮也稱為高溫超導懸浮(High Temperature Superconductor,HTS),其出現和發展相對較新,當前的研究主要集中在中國、俄羅斯、巴西等國家。

磁懸浮列車行駛的軌道大多鋪設在橋梁結構(包括軌道梁)之上,使得磁懸浮列車-橋梁耦合系統的動力特性成為磁懸浮列車研究的重點方向。在動力特性研究中,無法避免求解磁懸浮列車-橋梁的動力耦合方程。磁懸浮列車與橋梁間正是通過磁浮作用力進行相互動力耦合,故準確求解磁浮列車的磁浮力尤為重要。本文整理得出電磁懸浮、電動懸浮、高溫超導懸浮三種磁懸浮模式中磁浮力的計算式,并系統性地闡述了其優缺點及適用情況,以期能為不同制式磁懸浮列車-橋梁耦合系統或磁懸浮列車-軌道耦合系統的動力特性研究提供基礎性參考。

1 電磁懸浮

電磁懸浮(EMS)列車依靠車載電磁鐵與導磁性軌道之間產生的磁吸力平衡車輛負載,實現車體懸浮。EMS列車按行駛速度可分為高速與低速EMS列車,其結構見圖1。中低速EMS列車采用整體式懸浮與導向系統,即列車的懸浮與導向采用同一套電磁鐵系統,利用電磁鐵的自復位特性來提供導向力[4]。高速EMS列車采用分離式懸浮與導向系統,即列車的懸浮與導向采用兩套相互獨立的電磁鐵系統。車輛的整個懸浮系統由多個懸浮架串接形成,懸浮架又由電磁鐵與推進電機組成。而導向系統則由列車兩側的多個導向電磁鐵組成,高速EMS列車具有獨立的懸浮、導向功能[5]。EMS列車的懸浮氣隙約為8～12 mm,懸浮高度較小。EMS列車電磁力具有開環不穩定性,列車穩定性需要合適的控制系統來維持。從磁吸力的電磁原理出發,高速EMS與中低速EMS的磁浮力計算較為一致,本部分多借鑒公開成果較多的中低速EMS列車磁浮力的計算方法。

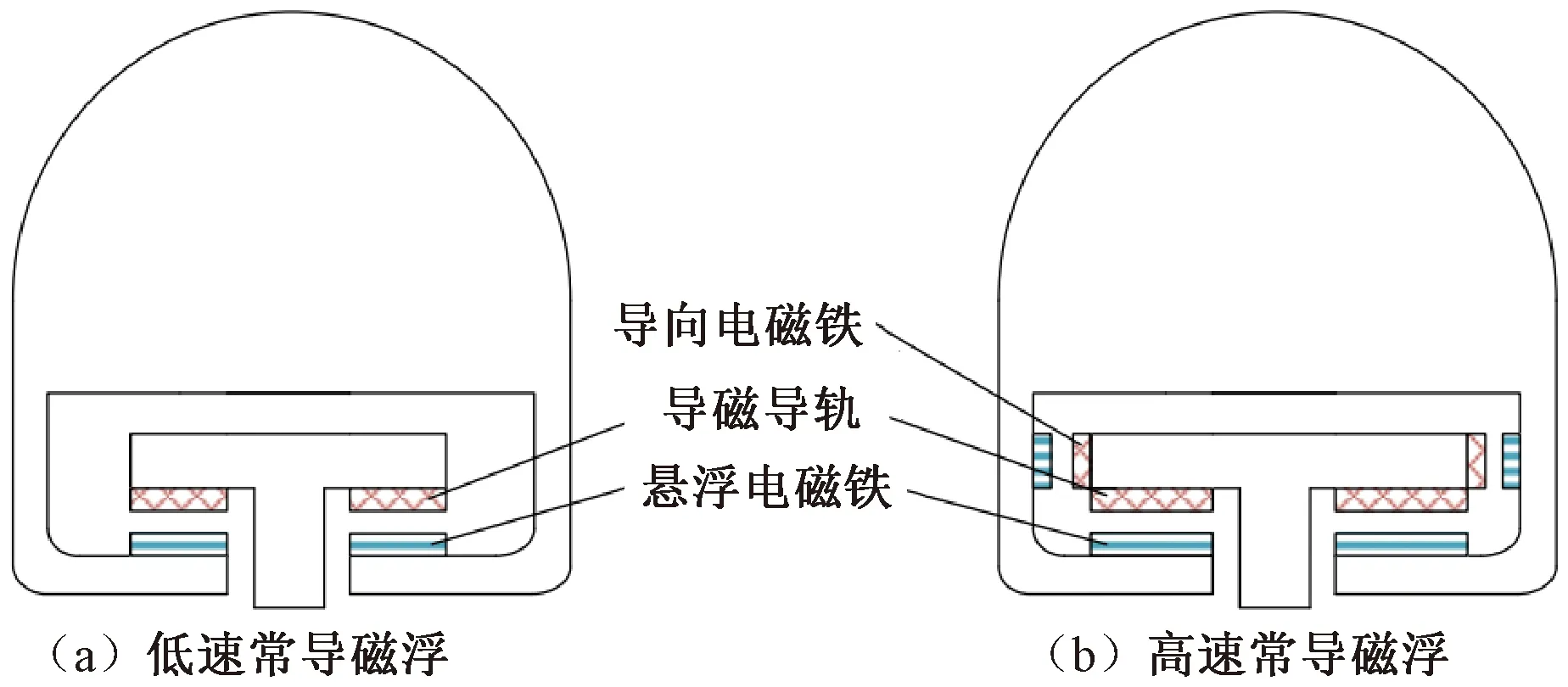
圖1 高速與低速EMS列車結構[4]

1.1 EMS列車的懸浮力計算

在早期的研究之中,一般將EMS列車懸浮力與懸浮氣隙變化的關系等效為線性彈簧-阻尼模型。即在懸浮平衡位置附近采用線性化的懸浮力與懸浮氣隙的關系,懸浮力Fz計算式為

Fz=F0+keΔ+ceΔ

( 1 )

式中:F0為電磁鐵的額定懸浮力,一般與負載相等;ke為等效磁隙剛度;ce為等效磁隙阻尼;Δ為懸浮氣隙相對平衡位置的變化值。

時瑾等[6]通過對電磁懸浮力特性的研究,為懸浮力線性化的處理方式提供了理論依據。該式成立的條件是Δ非常小,這時懸浮力的高階分量可以忽略。當氣隙波動較大時,受高階項影響計算結果偏差較大。該線性化懸浮力計算公式在懸浮氣隙小幅度變化時具有一定精度,而在懸浮氣隙大幅波動的情況下精度降低[1]。

輪軌列車軌道受到的是車輪集中力,磁懸浮列車與輪軌列車在受力的表現形式上存在較大差異。胡基士[7]指出磁浮列車軌道受到的是由懸浮架電磁鐵產生的分布式懸浮力,基于此推導得出電磁鐵的吸力方程為

( 2 )

式中:i為電磁線圈中的電流;ψ為電磁鐵線圈磁鏈;δ為懸浮氣隙。

式( 2 )為非線性微分方程,較難直接求解,在實際工程中,可忽略一些次要因素求解其近似值。如假定電磁鐵磁路在不飽和(線性)區段工作,則該吸力方程可簡化為[7]

( 3 )

式中:N為電磁鐵線圈匝數;G為電磁鐵等效總磁導,是氣隙的函數,可由磁路計算求得。

若將電流隨時間變化的函數代入式( 3 )即可求得EMS列車任意瞬時的懸浮力。

麥克斯韋(Maxwell)電磁吸力是近年來計算懸浮力的經典公式之一,麥克斯韋電磁吸力Fz的表達式為

( 4 )

式中:B為磁感應強度;A為磁極面積;μ0為空氣磁導率;Φ為磁通量,Φ=B·A。

式( 4 )簡單實用,使用時須滿足三個假設條件:①假設定子、轉子以及懸浮氣隙中的磁場均勻分布;②假設鐵芯呈線性不飽和特性;③忽略漏磁和磁滯的情況。由式( 4 )及這三個假設條件可以看出,Maxwell電磁吸力公式存在以下缺點:①不適合電磁鐵系統處于極小氣隙或大氣隙情況下電磁力的計算。當電磁鐵系統處于極小氣隙條件下時,易出現磁通飽和現象;當電磁鐵系統處于大氣隙條件下時,易出現氣隙磁場分布不均勻或漏磁增大等現象。此時,Maxwell電磁吸力公式的三個假設條件難以成立。②只能計算電磁鐵系統中豎向力總的數值大小而無法體現其受力形式,且無法計算電磁鐵產生的橫向力與縱向力[1]。

針對Maxwell經典計算公式的第一個缺點,即實際情況不符合三個假設條件而造成計算誤差,張亦靜[8]提出了修正懸浮力后實際的FR的計算式為

( 5 )

式中:FT為Maxwell電磁吸力公式計算的理論大小,即式( 4 )中的Fz;k1、k2、k3分別為磁場不均勻因素、鐵芯非線性因素、漏磁因素引起的誤差修正系數。

磁場的不均勻性在磁路法計算中主要體現在磁路長度的不同[9]。磁路分布見圖2。圖2中,l1為任意磁路的長度;l為磁路計算法所選取的中心磁路的長度。根據文獻[9]可知,當W<1/10即0.6l≤l1≤1.4l時,選取中心磁路l計算電磁力的誤差可以忽略不計,取修正系數k1=1。k2適用于懸浮氣隙大于2 mm、小于12 mm的情況,此時其數值大小主要受電磁鐵中電流大小的影響。根據文獻[8]中的實驗,當定子材料為QD122 G-30取向冷軋硅鋼片時,使用最小二乘法對k2進行擬合可得式( 6 )。根據文獻[8]中計算的誤差分布,可以得到不同氣隙下電磁力在鐵芯線性區間的誤差值,進而得到不同氣隙下對應的漏磁系數k3,使用最小二乘法對k3進行擬合可得式( 7 )。

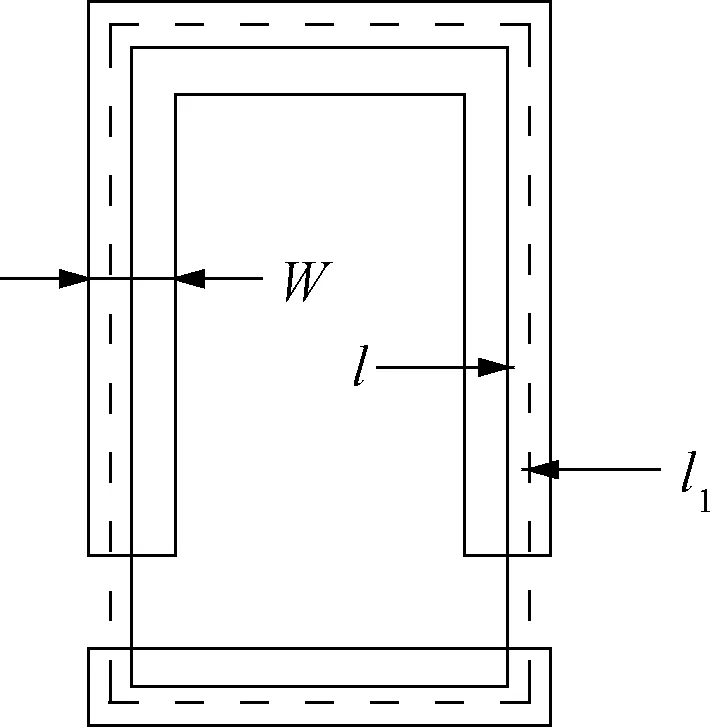
圖2 磁路分布圖[9]

( 6 )

( 7 )

1.2 三維磁浮力計算

針對Maxwell經典計算公式的第2個缺點,即只能計算電磁鐵豎向懸浮力而無法計算其余兩個方向的磁浮力,諸多學者對整體式懸浮與導向系統中的三維磁浮力計算進行了研究。Brzezina等[10]為了避免處理電磁鐵四角問題時須求解橢圓方程以及進行橢圓積分的麻煩,將細長型矩形磁極對四角問題簡化為兩個兩角問題,見圖3。運用保角變換獲得了二維平面內的懸浮力Fz與導向力Fy的計算式為

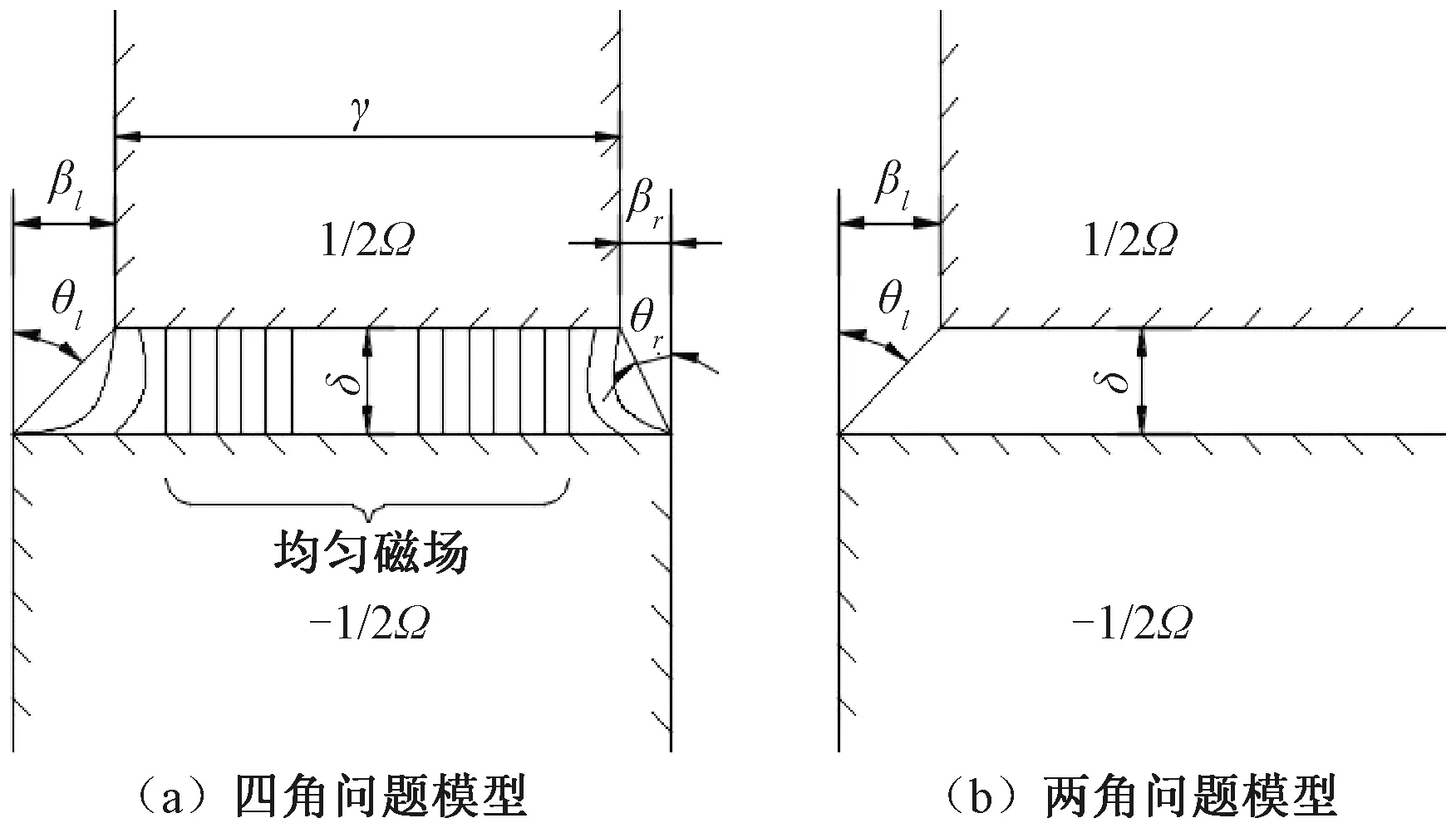
圖3 矩形磁極對模型[10]

( 8 )

( 9 )

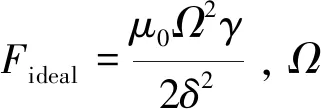
式( 8 )可進一步簡化為[10]

(10)

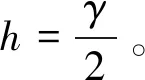
式( 8 )～式(10)是懸浮磁鐵處于小側滾條件下推導而得的。因為中低速EMS列車均設有防電磁鐵側滾裝置,能有效抑制列車運行過程中電磁鐵的側滾運動[11],所以可采用以上公式計算中低速EMS列車的懸浮力與導向力。

除了上述計算二維磁浮力公式,任曉博[4]還根據磁軌橫作用關系得出了新的二維磁浮力計算式為

(11)

(12)

式中:Δy為電磁鐵與導軌橫向偏移量,磁軌橫向作用關系見圖4。

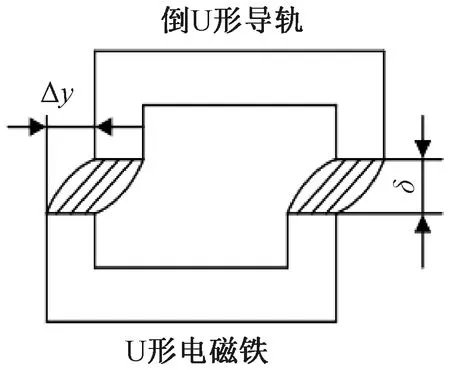
圖4 磁軌橫向作用關系[4]

由式(12)可知,磁極寬度γ越窄,橫向力Fy就越大。橫向錯位Δy越大,橫向力Fy亦越大。中低速EMS列車電磁鐵的橫向與豎向運動是相互耦合的[4]。當電磁鐵與導軌發生橫向偏移時,電磁力方向由豎向轉變為斜向,斜向電磁力的水平分力將使懸浮模塊回復到橫向平衡位置。當磁浮列車的懸浮氣隙發生變化時,控制系統會改變控制電磁線圈中的電流,電磁力大小會隨之改變,其水平分力也會發生變化。

三維磁浮力中還包含沿列車行駛方向的磁浮力,該方向的磁浮力又可分為驅動力與制動阻力。王桂榮等[12]根據EMS磁浮列車運行時所在位置處的定、轉子幾何分布和載荷分布,用隨時間變化的定、轉子磁動勢和勵磁函數來計算驅動磁懸浮列車的凸極直線同步電機的懸浮力Fz(x,t)與驅動力Fx(x,t)分別為

(13)

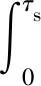
(14)

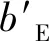
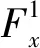
(15)

(16)

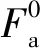
(17)

其中,dh為電磁鐵高度;σ為電導率;v為列車行駛速度;a為磁極寬度。

可以看出,式(15)、式(16)與式( 8 )～式(12)不同,反映了磁浮力大小與列車行駛速度復雜的非線性關系。

1.3 特殊情況下懸浮力計算

前述電磁力計算公式僅針對列車電磁鐵與軌道平行的情況,而張耿等[14]基于磁通管法推導了電磁鐵位于豎曲線時電磁懸浮力的解析表達式并進行了適當的簡化,凹曲線電磁懸浮力Fzajn簡化為

(18)

式中:r為豎曲線曲率半徑。

凸曲線電磁懸浮力Fztjn簡化為

(19)

根據文獻[14]中的仿真實驗結果可知,在不同情況下所得的擬合曲線基本吻合,且該豎曲線電磁懸浮力簡化公式具有較高的精確性。此外,式(18)、式(19)形式與Maxwell電磁吸力公式推導而得的懸浮力計算公式形式類似,且所需參數基本相同。

現有混合型電磁鐵大多采用電磁和永磁混合勵磁方式,這種混合形式有以下兩個優點。第一,提供相同大小的懸浮力時,混合型電磁鐵所需的電流相較于純電磁鐵所需的電流要小得多[15],極大地降低了磁懸浮列車的能耗。第二,與相同結構的純電磁鐵系統相比,將系統中的部分電磁鐵替換為永磁鐵會適當增加懸浮磁鐵的承載能力,從而增大列車等效的懸浮氣隙[16]。王蕓[16]沿用德國TR08磁浮列車架構,將懸浮磁鐵部分更換為電磁永磁混合磁鐵。進行如下假設:①忽略氣隙、繞組和永磁鐵的漏磁通;②磁路中鐵芯和導軌的磁導率無窮大,磁勢均勻地降落在氣隙和永磁鐵上;③氣隙中的磁場均勻分布;④軌道作用面的剛度系數無窮大,不考慮軌道本身的彈性振動或動態形變。推導得出混合型電磁鐵中單個閉合磁路產生的懸浮力為

(20)

式中:μm為永磁鐵相對磁導率;Sm為永磁鐵截面積;Hc為永磁鐵矯頑力;δm為永磁鐵厚度。式(20)所需參數均為電磁鐵與永磁鐵自身的固有參數。若取永磁鐵厚度δm=0,式(20)退化為純電磁鐵懸浮力Maxwell式( 4 )。

1.4 公式分析

懸浮力計算分為3部分:①將懸浮力與懸浮氣隙變化值關系(磁軌關系)線性化,推導得出的式( 2 ),該種方法僅適用于懸浮氣隙變化值較小的情況;②將根據磁懸浮系統力學分析的基本關系,假定電磁鐵磁路工作在不飽和(線性)區段,簡化而得的式( 3 );③Maxwell電磁吸力式( 4 )以及基于式( 4 )提出的修正方程式( 5 );值得注意的是,Maxwell電磁吸力公式須滿足2.1節提及的三個假設條件,這三個假設條件往往與實際的工程情況不符,因此,其修正公式提供了以對三個假設條件分別使用三個修正系數為思路的修正計算方法。

三維磁浮力計算包括懸浮力、導向力、驅動力與制動阻力。懸浮力與導向力的計算方法主要分為兩部分:①將長型矩形磁極對二維四角問題簡化為兩個兩角問題,運用保角變換推導得出懸浮力與導向力的計算式( 8 )、式( 9 ),該公式適用于懸浮磁鐵處于小側滾條件;②根據磁軌橫向作用關系推導得出懸浮力與導向力的計算式(11)、式(12),該公式說明了中低速EMS列車的橫向運動與豎向運動相互耦合的關系。磁浮列車的凸極直線同步電機的驅動力式(14)是使用定子、轉子磁動勢與勵磁曲線推導得出的。制動阻力的計算式(16)是通過對氣隙磁場分布與電磁鐵速度特性的研究分析得出的,該公式反映了制動阻力與列車行駛速度復雜的非線性關系。

特殊情況下的懸浮力計算分為兩部分:①中低速EMS列車經過凹曲線與凸曲線的懸浮力計算式(18)、式(19)是基于磁通管法推導得出的,該公式計算參數與Maxwell電磁吸力公式相似,對中低速EMS列車具有一定的適用性;②混合磁鐵中單個磁路的懸浮力計算式(20)是根據德國TR08列車架構,將懸浮磁鐵部分替換為電磁永磁混合磁鐵推導得出的,使用該公式時,除了需滿足Maxwell電磁吸力公式的三個假設條件外,還需假設軌道作用面剛度無窮大。

2 電動懸浮

與EMS型列車的懸浮原理不同,電動懸浮(EDS)列車依靠運動磁場在導體軌道中產生的渦流實現斥力懸浮。其斥力較大,可使懸浮氣隙達100 mm,降低了列車對軌道變形與控制系統精度的要求。因此,EDS列車具有高速穩定性好,且不需要主動控制等優點。但是EDS列車在靜止時無法懸浮,若要使其懸浮,須使列車達到一定的行駛速度,這個速度也被稱為起浮速度。因此,在EDS列車起浮之前,需借助輪軌在軌道上行駛。現有的EDS列車按產生運動磁場的物體主要分為永磁EDS列車與低溫超導EDS列車。永磁EDS列車的軌道鋪設鋁板。低溫超導EDS列車的軌道最初被設計為鋪設導體板,該種結構形式會產生較大的電磁阻力,從而引起較大的能量損耗。為了降低能量損耗,Danby等[17]提出用零磁通線圈(即8字線圈)代替導體板的方案。

2.1 永磁EDS列車磁浮力計算

永磁EDS列車主要是利用Halbach結構排列的永磁體產生的磁場切割導體板,產生感應電流從而達到懸浮狀態,具有結構簡單且節能的特點。Halbach結構陣列中相鄰永磁體的磁化方向相差一個固定的角度。陳殷等[18]使用Ansys軟件對Halbach永磁EDS系統受力進行了數值計算,研究了懸浮力隨系統參數改變的變化規律,得到懸浮力Fz(d)簡單有效的表達式為

(21)

式中:τ為Halbach陣列極距;k為高度極距比;m為氣隙極矩比;F0(d)為極距、矯頑力、高度極距比、氣隙極距比分別取τ0、Hc0、k0、m0時的受力,也稱為反應板厚度為d時的標準力;F(k)、F(k0)為高度極矩比分別取k、k0時的受力。

由式(21)可以看出,懸浮力與極距τ、矯頑力Hc成正比。從文獻[18]可知,懸浮力Fz(d)隨高度極矩比k、氣隙極矩比m分別遵循某一固定曲線,且該曲線不隨其他因素變化,具有較好的普遍意義。

李云鋼等[19]從電磁感應定律和電磁力定律出發推導得出永磁EDS列車中一個Halbach排列周期內的平均懸浮力Fz與阻力Fx的計算式分別為

(22)

(23)

式中:B0為永磁體產生的磁感應強度;f為空間頻率,f=2π/τ;L0為電感;vT=R/kL0,R為導體的電阻。

式(23)物理意義明確,便于理解磁阻力不會隨速度增加而一直增加。在一個Halbach排列周期內,導體穿越磁場時的速度v與此時的懸浮氣隙δ的變化幅度不大。為計算方便,可假設Halbach排列周期內速度v與懸浮氣隙δ為常數。從式(22)、式(23)可以看出,懸浮力隨速度增大而增大,但當速度達到一定數值時,懸浮力不再繼續增大;阻力隨速度增大先快速增大,當速度達到一定數值時,阻力又隨速度增大而逐漸減小。

陳殷[20]分別采用麥克斯韋張量法與磁荷法推導得出Halbach陣列永磁EDS列車三維磁浮力的解析計算公式經文獻[20]的實驗驗證,該三維磁浮力的解析計算式的計算結果與實驗結果的平均誤差僅為1%。

2.2 低溫超導EDS列車磁浮力計算

軌道鋪設常導8字零磁通線圈是低溫超導EDS列車的主要形式。低溫超導EDS列車依靠車載低溫超導線圈與軌道8字零磁通線圈發生錯位時會產生回復力的特性,在能量損耗較低的前提下實現了自懸浮和自導向。王琳[21]從描述超導體宏觀電磁特性的Maxwell方程出發,確定超導體表面屏蔽電流的分布,進而求得低溫超導EDS系統中的兩同軸環形線圈的軸向作用力(靜態懸浮力)Fz的計算式為

(24)

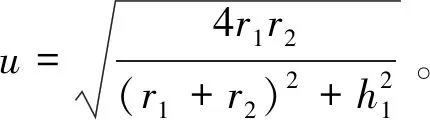
張娟[22]通過推導發現,一對交叉連接的8字線圈和超導線圈之間的懸浮力和導向力與線圈間的相對位置和車輛運行速度有關。并且導軌線圈隨著超導線圈縱向運行,受到的力為簡諧分布力,周期為τsc/v,τsc為超導線圈極距。得到列車縱向運行時引起的左、右兩側超導線圈受到的總的懸浮力Fz1、Fz2和總的導向力Fy1、Fy2的計算公式。

這對于確定參數的低溫超導EDS系統,懸浮力與導向力大小主要受列車運行速度的影響,其次受懸浮氣隙與導向氣隙的影響。

Cai等[23]基于動態電路理論,建立了8字零磁通軌道線圈無交叉連接EDS列車系統中懸浮導向結構的等效電路模型,采用能量法推導得出超導磁體與軌道線圈間的懸浮力Fz、導向力Fy、磁阻力Fx的計算公式。使用這3個公式進行計算前須確定列車的速度與懸浮間隙。另外,這3個公式的局限性在于不能完全反映低溫超導EDS列車電磁力、速度與加速度的動態特性。

2.3 公式分析

永磁EDS列車懸浮力的計算式(21)雖不具有通用性,但為Halbach永磁EDS系統的懸浮力計算提供了解決思路。永磁EDS列車的一個Halbach排列周期內的平均懸浮力Fz與阻力Fx式(22)、式(23)具有良好的適用性,并且驗證了EDS系統中,懸浮力不會隨速度增大而無限增大、阻力隨速度增大先增大后減小的特性。基于麥克斯韋張量法和磁荷法兩種不同的方法,均可得出永磁EDS列車的三維磁浮力計算公式。

低溫超導EDS列車的懸浮力計算公式不具有通用性,但其揭示了低溫超導EDS系統的中懸浮力與線圈電流、間隙變化之間的關系。低溫超導EDS列車總的懸浮力與導向力計算公式展現出低溫超導EDS系統中懸浮力與導向力第一影響因素是列車運行速度,其次是懸浮氣隙與導向氣隙。低溫超導EDS列車的三維磁浮力計算公式是基于動態電路理論,采用能量法推導得出的。

3 高溫超導懸浮

超導體具有兩個基本特性:①零電阻,即當溫度低于一定值后,超導體的電阻低至現有設備無法測量得到;②邁納斯效應,即超導體無論是在場冷(使超導體先降溫,后施加磁場)條件下還是在零場冷(先給超導體施加磁場,后降溫)條件下從一般態相變至超導態,超導體的磁通量恒等于零。其中邁納斯效應是區別理想導體與超導體的重要依據。與超導體不同,理想導體除了具有零電阻特性外,在其降溫過程中導體內的磁通量凍結不變。邁納斯效應與理想導體的情況見圖5。圖5中,N表示導體處于一般態;S表示導體處于超導態。高溫超導懸浮中的“高溫”是相對低溫超導電動懸浮中的“低溫”而言的,低溫超導須使溫度接近絕對零度,即達到-269 ℃,高溫超導僅須使溫度達到-196 ℃。

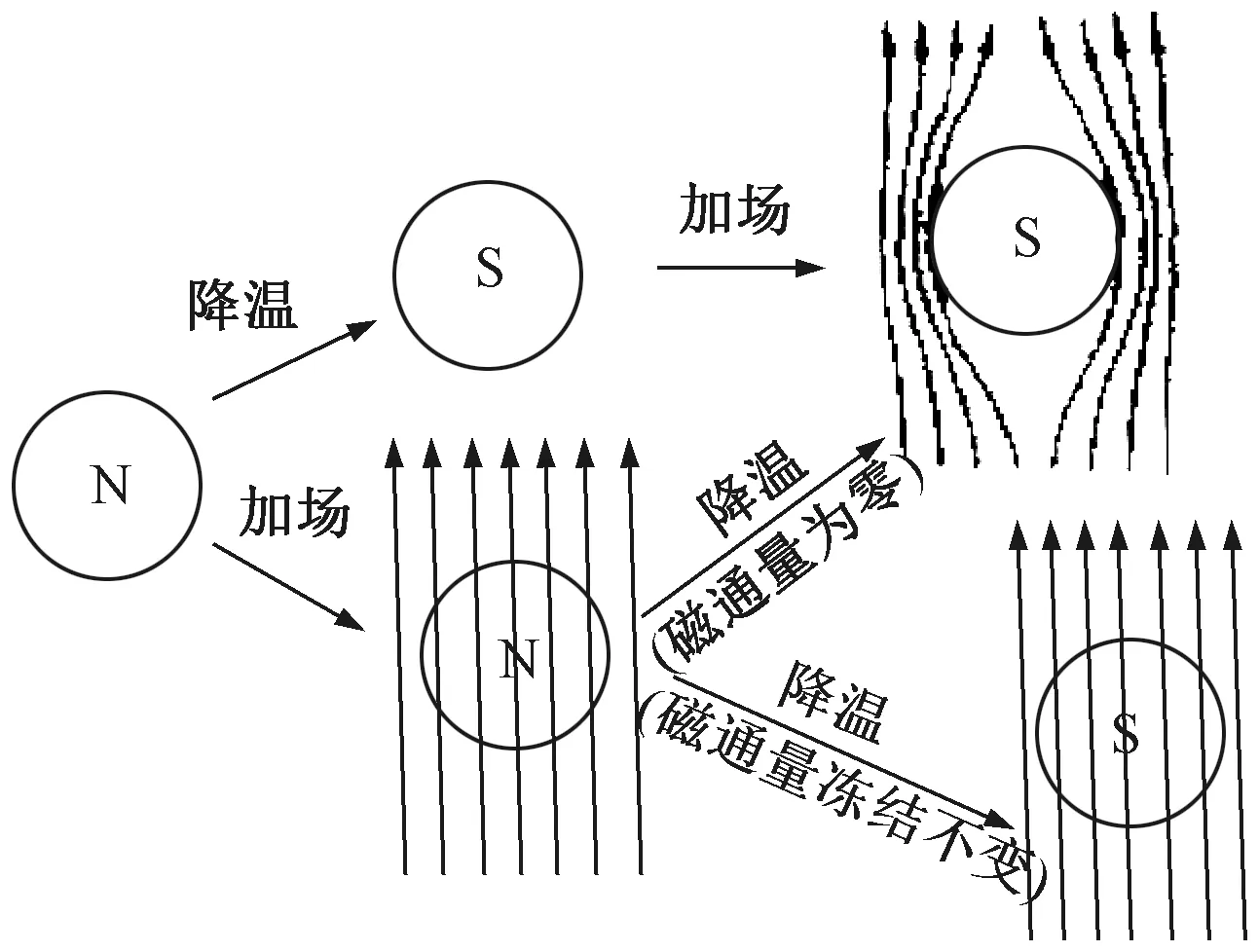
圖5 邁納斯效應與理想導體情況比較[24]

高溫超導懸浮(HTS)列車采用永磁體做軌道,高溫超導體置于列車之上。HTS列車一般采用非理想第二類高溫超導體作為車載磁體,該導體內存在晶體缺陷,磁通線會受這些缺陷束縛從而出現磁通釘扎現象。利用非理想第二類高溫超導體在混合態中的磁通釘扎效應可實現HTS列車自懸浮、自導向和沿永磁軌道前行[3]。HTS列車的懸浮與導向均通過磁通釘扎效應實現,具有無需主動控制、自穩定、自懸浮、自導向等特點。相較于低溫超導EDS列車而言,HTS列車還能實現靜止懸浮,無需輔助輪軌。沿行駛方向不存在固有磁阻力,降低了能耗。

3.1 HTS列車的懸浮力計算

高溫超導體的電阻為0,其內產生的感應電流會一直存在。由楞次定律,感應電流產生的磁場與引起感應電流的磁場方向相反,劉文旭等[2]指出永磁體與高溫超導體之間作用力可表示為

(25)

式中:H為超導體內的場強;M為超導體內的磁化強度;V為超導體內的有效磁化體積。

Hao等[25]采用有限元法分析了HTS系統的懸浮力,并根據渦流分布和力分析結果使用了一種鏡像法,以簡化HTS系統中單個線圈的飽和懸浮力Fzs計算,其計算公式為

Fzs=2πRaBrFcoil

(26)

式中:Ra=(Rin+Rout)/2為HTS線圈的平均半徑;Fcoil=N·Iapp,Iapp為HTS線圈的工作電流;Br為圓柱坐標下鏡像線圈在HTS線圈區域感應的磁場分量,其計算式為

(27)

其中,hs=2δ為HTS線圈到鏡像線圈的距離;Es和Ks為線圈形狀和尺寸對應的參數,根據高溫超導線圈參數分別設置為1.044和3.093。

由于單個HTS線圈不僅會受自身感應磁場的影響,還會受到其他HTS線圈感應磁場的影響,這使得鏡像法的解析解十分復雜。此時可采用基礎的電磁懸浮力計算式為

(28)

式中:Jc為超導臨界電流密度;Bp為永磁體中的磁通量密度。

3.2 HTS列車的二維磁浮力計算

張興義[26]通過對凍結鏡像模型的改進,推導得出HTS系統導向力Fy、懸浮力Fz的計算式分別為

(29)

(30)

式中:m1為永磁體簡化而得的磁偶極子數量;m2為超導體表面屏蔽電流形成的磁場簡化而得的抗磁鏡像磁偶極子數量;m3為高溫超導體在初始冷卻位置上冷卻形成凍結磁通簡化而得的凍結鏡像磁偶極子數量;hf為高溫超導體初始冷卻時距離磁場的高度。

磁浮力與懸浮氣隙、導向氣隙具有一一對應關系。值得注意的是,文獻[26]中指出該公式無法計算零場冷情況下懸浮系統的導向力,原因是當場冷高度趨近無窮大(零場冷情況)時,式(29)計算所得的導向力為0。

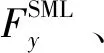
-2Lxμ0[H1sin(krvt)+H2cos(krvt)+C]

(31)

(32)

式中:Lx為高溫超導塊材沿行駛方向的長度;By、Bz分別為磁感應強度的兩個分量;kr為橫向力剛度與懸浮力的比值系數,krvt為運動行程;χx、χy、χz均為高溫超導塊材磁化曲線的幾何參數;H1、H2分別為關于sin(krvt)、cos(krvt)的函數;C為不含sin(krvt)、cos(krvt)的常數項,其表達式分別為

(33)

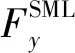
(34)

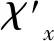
根據文獻[27]中實驗,導向力剛度主要受場冷高度和工作高度的影響。當場冷高度一定時,導向力剛度隨工作高度的降低而增加,當工作高度一定時,導向力剛度隨場冷高度的降低而增加。可見,若需保持SML子系統較高的導向力剛度,可使HTS系統在較低的場冷高度和工作高度下運行。

3.3 公式分析

一維磁浮力計算公式分為三部分:①從微觀角度出發,描述永磁體與高溫超導體之間的相互作用力,宏觀上則表現為超導體與永磁體之間的懸浮力,其計算公式為式(25);②采用有限元法分析HTS系統的懸浮力,然后根據其渦流分布與力分析結果使用鏡像法,簡化得出飽和懸浮力的計算式(26);③式(27)僅適用于單個HTS線圈的飽和懸浮力計算,HTS系統中多個線圈自身的感應磁場會相互影響,此時可采用基礎電磁懸浮力的計算式(28)。

二維磁浮力計算公式分為兩部分:①通過對凍結鏡像模型改進推導得出HTS列車的導向力與懸浮力式(29)、式(30),其中導向力公式無法計算零場冷情況;②通過對高溫超導—永磁混合懸浮列車的磁力特性分析得出SML子系統的導向力、懸浮力與導向剛度的計算式(31)～式(34),由該公式可知懸浮力隨場冷高度的增大而增大,導向力剛度隨場冷高度、工作高度的增大而減小。

4 結論

本文總結了電磁懸浮(EMS)、電動懸浮(EDS)與高溫超導懸浮(HTS)三種不同懸浮模式特性及磁浮力計算方式。主要結論如下:

1)電磁懸浮列車采用常導體作為線圈繞組產生電磁吸力實現懸浮與導向,具有結構簡單(無需冷卻系統)、可靜懸浮等特點。線性化的懸浮力公式簡單易用,但僅適用于較小的懸浮氣隙變化。懸浮力計算以Maxwell公式最為經典,但在特殊條件下具有局限性,可采用磁場不均勻修正、鐵芯非線性修正、漏磁修正將Maxwell公式拓展到極小氣隙或極大氣隙條件。通過將長型矩形磁極對二維四角問題簡化為兩個兩角問題,運用保角變換可得到小側滾條件下二維平面內的懸浮力、導向力,也可通過磁軌橫向作用關系推導得出二維平面內的懸浮力、導向力。使用定子、轉子磁動勢與勵磁函數或氣隙磁場分布特性得到懸浮力、阻力的計算公式。對于曲線軌道、電磁與永磁混合型電磁鐵,具有不同的懸浮力計算公式。

2)永磁EDS列車利用車載永磁體與軌道導體板渦流磁場間的斥力實現懸浮,具有結構簡單、成本低、車體質量輕、懸浮氣隙大等特點。通過磁場數值模擬可獲得表達式,為Halbach永磁EDS系統的懸浮力計算提供了思路。在一個Halbach排列周期內從電磁感應定律和電磁力定律出發推導得到了適用性較好的平均懸浮力與阻力計算公式。基于麥克斯韋張量法和磁荷法,可得到永磁EDS列車的三維磁浮力計算公式。

3)低溫超導EDS列車利用車載低溫超導體切割軌道線圈產生的斥力實現懸浮,具有自懸浮、自導向、懸浮氣隙大、無需主動控制,適合高速行駛等特點。從超導體宏觀電磁特性Maxwell方程出發,或基于動態電路理論采用能量法,可推導得到磁浮力表達式。有學者提出懸浮力與車輛運行速度有關,建立了反映速度影響的懸浮力、導向力表達式。

4)高溫超導懸浮列車利用車載高溫超導體與永磁軌道間的磁通釘扎效應實現列車懸浮與導向,具有自懸浮、自導向、高穩定性、懸浮氣隙大以及無磁阻力、可靜懸浮等特點。從超導體磁場理論或有限元數值模擬方式均可建立超導體與永磁體之間的懸浮力公式,有限元中可采用鏡像法模擬渦流分布簡化分析過程。通過改進的凍結鏡像模型或者磁力特性分析可建立高溫超導懸浮列車懸浮力與導向力的公式。