基于升弓高度的受電弓氣動(dòng)抬升系數(shù)計(jì)算方法與分析

宋詩揚(yáng)，韓通新

(1.中國鐵道科學(xué)研究院 研究生部，北京 100081；2.中國鐵道科學(xué)研究院集團(tuán)有限公司 機(jī)車車輛研究所，北京 100081)

受電弓的主要作用是通過接觸線使列車完成良好可靠的受流過程,這需要受電弓滑板與接觸線間保持一定弓網(wǎng)接觸力。接觸力過高會(huì)對接觸導(dǎo)線造成機(jī)械磨耗,嚴(yán)重時(shí)會(huì)形成硬彎和局部不平順,加大弓網(wǎng)之間的振動(dòng),使受流不穩(wěn)定;接觸力過低則會(huì)使碳滑板與接觸導(dǎo)線間不能完全接觸或離線而產(chǎn)生燃弧和火花,嚴(yán)重影響弓網(wǎng)受流質(zhì)量,同時(shí)也會(huì)降低系統(tǒng)總體壽命。弓網(wǎng)接觸力是靜態(tài)接觸力、氣動(dòng)抬升力、摩擦接觸力和垂直方向上的質(zhì)量慣性力的合力。在高速情況下,氣動(dòng)抬升力是弓網(wǎng)接觸力的主要組成部分,其大小隨速度提升急劇增大,因此氣動(dòng)抬升力在高速弓網(wǎng)關(guān)系研究中至關(guān)重要。

為此國內(nèi)外眾多學(xué)者對受電弓的空氣動(dòng)力影響開展了大量研究。文獻(xiàn)[1]分析了上、下臂桿直徑對高速受電弓氣動(dòng)抬升力的影響,發(fā)現(xiàn)上、下臂桿直徑變化在開口和閉口方向運(yùn)行時(shí),對受電弓的氣動(dòng)抬升力產(chǎn)生相反的影響。文獻(xiàn)[2]研究了受電弓弓頭的外形幾何結(jié)構(gòu),指出改變弓頭外形并利用不同高度和斜度的檔板可以提高高速列車受電弓的氣動(dòng)性能。文獻(xiàn)[3]探討了高速列車在過隧道時(shí)受電弓的空氣動(dòng)力性能,發(fā)現(xiàn)受電弓氣動(dòng)抬升力在隧道入口和出口時(shí)出現(xiàn)峰值,而隧道內(nèi)的氣動(dòng)抬升力顯著上升。文獻(xiàn)[4]采用風(fēng)洞試驗(yàn)方法,得出在受電弓前部安裝各種導(dǎo)流罩和風(fēng)擋可以改善其空氣動(dòng)力性能的結(jié)論。文獻(xiàn)[5]提出了受電弓的空氣抬升力計(jì)算方法,總結(jié)出在受電弓橫桿上加裝導(dǎo)流板以及在受電弓支持絕緣子底部加一個(gè)支撐座以提高受電弓空氣動(dòng)力性能的兩個(gè)方案。文獻(xiàn)[6]對受電弓導(dǎo)流板的氣動(dòng)特性進(jìn)行了二維數(shù)值研究,發(fā)現(xiàn)導(dǎo)流板的橫截面翼型在一定角度下能產(chǎn)生有效的氣動(dòng)升力,從而改善受電弓的氣動(dòng)性能。文獻(xiàn)[7]通過對兩種受電弓進(jìn)行風(fēng)洞試驗(yàn),發(fā)現(xiàn)不同受電弓弓架的空氣動(dòng)力性能存在較大差異。

本文從現(xiàn)場實(shí)際應(yīng)用角度出發(fā),分析了不同線路中接觸線高度差異造成的不同升弓高度對空氣動(dòng)力性能的影響。基于氣動(dòng)抬升力基本公式和受電弓各臂桿間的幾何關(guān)系推導(dǎo)出升弓高度與氣動(dòng)抬升力和氣動(dòng)抬升系數(shù)的數(shù)學(xué)模型,并進(jìn)行理論分析;使用計(jì)算流體力學(xué)軟件Ansns Fluent對受電弓進(jìn)行仿真建模,并通過調(diào)整運(yùn)行方向、速度和升弓高度,得到開、閉口運(yùn)行方向下氣動(dòng)抬升系數(shù)與受電弓升弓高度之間的關(guān)系,驗(yàn)證基于數(shù)學(xué)計(jì)算模型的理論分析;對國內(nèi)某線路通過壓力傳感器測量的方法收集氣動(dòng)抬升力數(shù)據(jù),對比前面的分析與結(jié)論。其中,模型仿真數(shù)值求解采用目前最常見的SSTk-ω湍流模型,在眾多文獻(xiàn)中均有應(yīng)用:如文獻(xiàn)[8]采用該模型計(jì)算雙滑板受電弓不同滑板間距條件下的氣動(dòng)抬升力;文獻(xiàn)[9]使用該模型求解受電弓導(dǎo)流裝置不同擋風(fēng)角度下的氣動(dòng)抬升力;文獻(xiàn)[10]利用該模型計(jì)算受電弓不同安裝位置的空氣動(dòng)態(tài)力;文獻(xiàn)[11]使用該模型得到升弓和降弓狀態(tài)下高速列車受電弓氣動(dòng)抬升系數(shù)和氣動(dòng)阻力系數(shù);文獻(xiàn)[12-13]驗(yàn)證了使用仿真軟件和該模型計(jì)算受電弓氣動(dòng)抬升力的準(zhǔn)確性;文獻(xiàn)[14]基于該模型計(jì)算4種類型的受電弓在不同運(yùn)營場景中的氣動(dòng)抬升力;文獻(xiàn)[15]使用該模型計(jì)算受電弓不同安裝位置時(shí)的氣動(dòng)阻力和升力的時(shí)域均值;文獻(xiàn)[16]利用該模型計(jì)算不同受電弓結(jié)構(gòu)影響下的氣動(dòng)阻力;文獻(xiàn)[17]基于該模型模擬明線軌道上單列高速列車的氣流流場,并給出受電弓等各部件的氣動(dòng)阻力相對列出總氣動(dòng)阻力的比值。

1 受電弓空氣動(dòng)力計(jì)算模型

1.1 基本公式

空氣氣流作用在受電弓上的機(jī)械力分解為水平氣動(dòng)阻力和垂直氣動(dòng)抬升力。其中氣動(dòng)抬升力直接影響弓網(wǎng)受流質(zhì)量和受電弓滑板與接觸線間的磨耗,因此本文重點(diǎn)研究氣動(dòng)抬升力和氣動(dòng)抬升系數(shù)的計(jì)算。

氣動(dòng)抬升力FL計(jì)算式為

( 1 )

式中:ρ為空氣密度;v為受電弓邊界速度;A為迎風(fēng)面積;CL為氣動(dòng)抬升系數(shù)。

在不考慮壓力對空氣密度變化的影響時(shí),ρ可視為一個(gè)常量;迎風(fēng)面積A由受電弓本體結(jié)構(gòu)決定,也是一個(gè)常量,令A(yù)=A′sinθ,A為計(jì)算面積,A′為實(shí)際面積,θ為受電弓表面相對平行方向氣流的夾角,迎風(fēng)面積是受電弓各部分相對空氣氣流的表面積,基于桿件的幾何形狀計(jì)算得出;CL取決于升弓角度和開閉口行駛方向等因素,計(jì)算相對復(fù)雜,一般通過仿真或風(fēng)洞、線路試驗(yàn)得出。

升弓高度和開、閉口運(yùn)行方向會(huì)影響氣動(dòng)抬升力系數(shù),原因是受電弓本體幾何結(jié)構(gòu)和臂桿長度是既定的,升弓高度決定了各臂桿之間和下臂桿間與底座間的夾角。氣流相對于受電弓的運(yùn)行方向是水平的,任何非平行于氣流運(yùn)行方向的角度都會(huì)使該臂桿存在一個(gè)非零的氣動(dòng)抬升系數(shù)。將各臂桿與氣流水平之間的夾角α定義為風(fēng)攻角。由于風(fēng)攻角直接影響氣動(dòng)抬升系數(shù),因此將各臂桿間夾角以風(fēng)攻角表示,見圖1,例如上下臂桿間夾角等于風(fēng)攻角α2+α5。

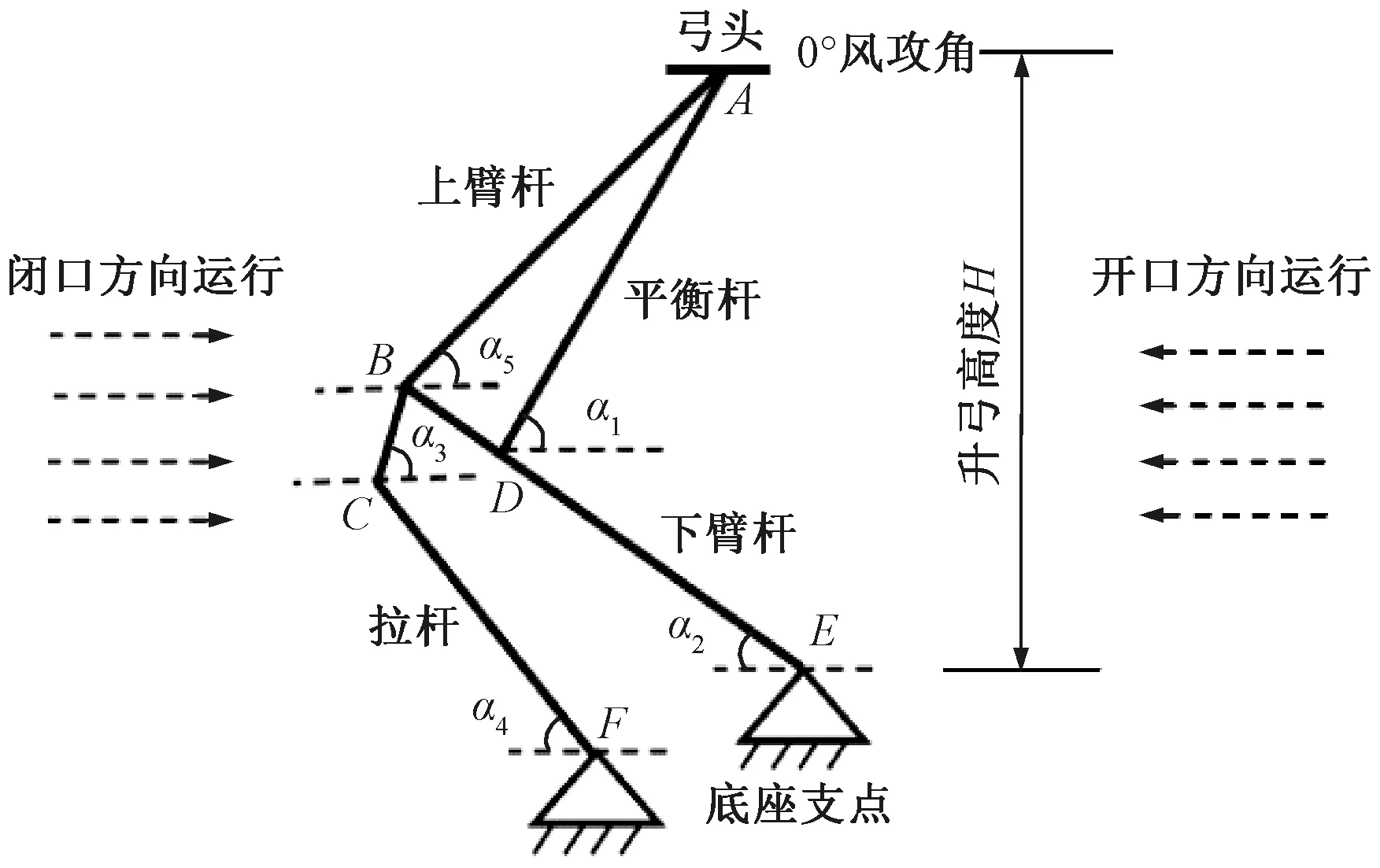
圖1 風(fēng)攻角示意

1.2 風(fēng)攻角計(jì)算

由圖1可知,升弓高度H的表達(dá)式為

H=LADsinα1+LDEsinα2=LABsinα5+

LBCsinα3+LCFsinα4

( 2 )

式中:LAD、LDE、LAB、LBC、LCF為各臂桿長度,這些參數(shù)均為已知項(xiàng)。

等式兩邊整理可得

( 3 )

在升弓時(shí),受電弓各臂桿并非獨(dú)立運(yùn)作,而是在電動(dòng)彈簧或氣囊氣壓的作用下聯(lián)動(dòng),其余臂桿按照一定比例角度同時(shí)升起。基于這一特點(diǎn),可將測量某一升弓高度時(shí)各臂桿夾角間的比例關(guān)系表示為

α2+α5=k(α1+α2)=k′(α3+α4)=

k″[α5+(180°-α3)]

( 4 )

式中:4個(gè)等式分別表示αABE、αADE、αBCD和αABC。

又知兩支點(diǎn)處夾角比例可表示為

( 5 )

由式( 5 )可解得

( 6 )

代入式( 3 )中得

( 7 )

此時(shí),等式僅有兩個(gè)變量,可寫出α1和α5的關(guān)系式。代入式( 6 )中可分別將α2、α3、α4、α5用α1表示。

又知式( 2 )中等式兩邊均等于升弓高度H,因此可以寫出升弓高度相對風(fēng)攻角α1的關(guān)系式。同樣方法,可以基于升弓高度求出其余風(fēng)攻角,這里不再詳細(xì)贅述。

得到α1～α5后,可以計(jì)算氣動(dòng)抬升系數(shù)。

1.3 氣動(dòng)抬升系數(shù)計(jì)算

平衡桿處受力較小,且點(diǎn)D處不存在力矩傳遞。為簡化計(jì)算,根據(jù)文獻(xiàn)[18],將作用在平衡桿的力進(jìn)行等效處理。受力分析見圖2。

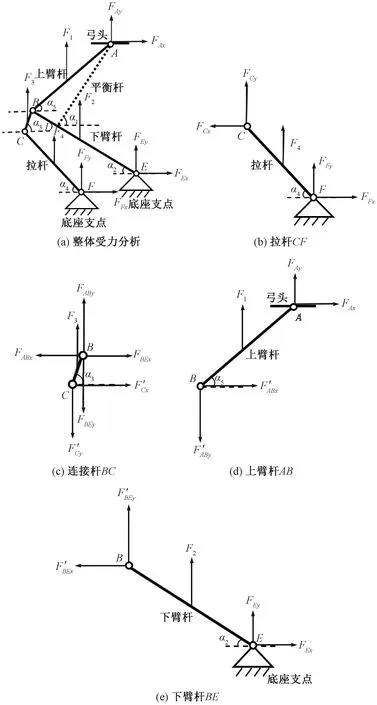
圖2 受力分析

拉桿CF受力分析

( 8 )

連接桿BC受力分析

( 9 )

上臂桿AB受力分析

(10)

下臂桿BE受力分析

(11)

由于LAB、LBE、LEF、LAC、LCD、LDG長度已知,α2、α3、α4、α5已由前面計(jì)算得知。因此,可對式( 8 )～式(11)求解,得到各臂桿連接處氣動(dòng)抬升力。再將氣動(dòng)抬升力代入式( 1 )中可反推得到相應(yīng)氣動(dòng)抬升系數(shù)CL為

(12)

雖然由風(fēng)攻角直接計(jì)算氣動(dòng)抬升系數(shù)有難度,但兩者關(guān)系比較直觀:當(dāng)風(fēng)攻角取值較低時(shí),氣動(dòng)抬升系數(shù)與風(fēng)攻角呈正相關(guān)。考慮我國接觸線高度普遍為5.15～6.45 m,此高度限制下,開口方向運(yùn)行的受電弓的各臂間風(fēng)攻角不會(huì)超過上述關(guān)系臨界值,因此升弓高度越高,空氣動(dòng)態(tài)性能越差。

受電弓閉口方向運(yùn)行時(shí),各風(fēng)攻角取值與開口方向相反,因此一般情況下,閉口方向運(yùn)行的受電弓氣動(dòng)抬升系數(shù)和氣動(dòng)抬升力均高于開口方向。同時(shí),閉口方向的升弓高度與氣動(dòng)抬升系數(shù)呈負(fù)相關(guān)。這一結(jié)論在下述仿真和試驗(yàn)分析中再次驗(yàn)證。

2 受電弓空氣動(dòng)力仿真模型

2.1 受電弓模型

使用Ansys Fluent仿真軟件建立受電弓3D幾何模型。由于原廠CAD模型細(xì)節(jié)繁多,仿真計(jì)算費(fèi)用高且對結(jié)果影響甚微,因此采用簡化模型進(jìn)行模擬仿真。各臂桿長度尺寸參考實(shí)際測量數(shù)值,受電弓3D仿真模型見圖3。受電弓最大升弓高度2 600 mm,兩滑板間距離580 mm,滑板長、寬分別為1 060、58 mm。

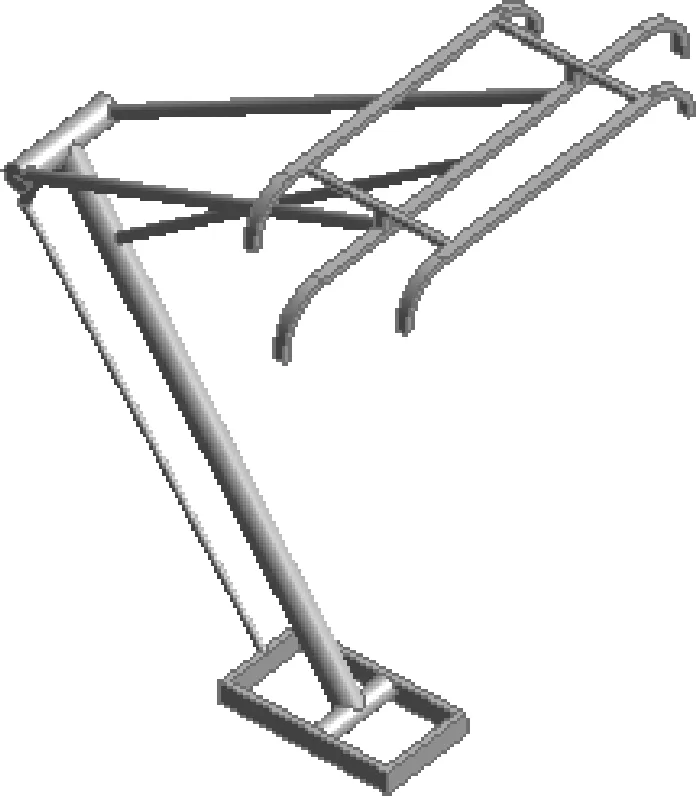
圖3 受電弓3D仿真模型

空氣動(dòng)力學(xué)仿真中,墻壁等障礙物對氣流動(dòng)力反射效果明顯(如隧道內(nèi)),因此應(yīng)盡可能擴(kuò)大計(jì)算區(qū)域,但過大也會(huì)造成網(wǎng)格面積劃分過于粗糙且易忽略邊界處空氣作用力影響和受電弓主要細(xì)節(jié)等問題。最終確定的計(jì)算區(qū)域?yàn)?.00×104mm×2.00×104mm×1.00×104mm(長×寬×高),氣流進(jìn)出口距受電弓中心點(diǎn)均為2.50×104mm。采用非線性離散網(wǎng)格,受電弓表面最小網(wǎng)格為3.91 mm,外部計(jì)算區(qū)域最小網(wǎng)格為14.59 mm,成漸變趨勢,最小曲率半徑2.92 mm, 曲度法向角18°。受電弓表面共計(jì)77個(gè)網(wǎng)格面,仿真計(jì)算面積見圖4。出口截面表壓力為0 Pa,氣流入口界面速度設(shè)為受電弓實(shí)際運(yùn)行速度(無風(fēng)下仿真)。對250、300、350、400 km/h共4個(gè)速度級的開、閉口兩個(gè)運(yùn)行方向的受電弓進(jìn)行空氣動(dòng)力仿真。空氣密度設(shè)為1.225 kg/m3,空氣黏滯系數(shù)為1.789×10-5Pa·s。

圖4 仿真計(jì)算面積

2.2 固定升弓高度仿真結(jié)果

在升弓高度不變的情況下,基于目前最為常用的SSTk-ω算法模型對受電弓仿真進(jìn)行數(shù)值求解,得出不同運(yùn)行方向、速度的仿真結(jié)果見表1。

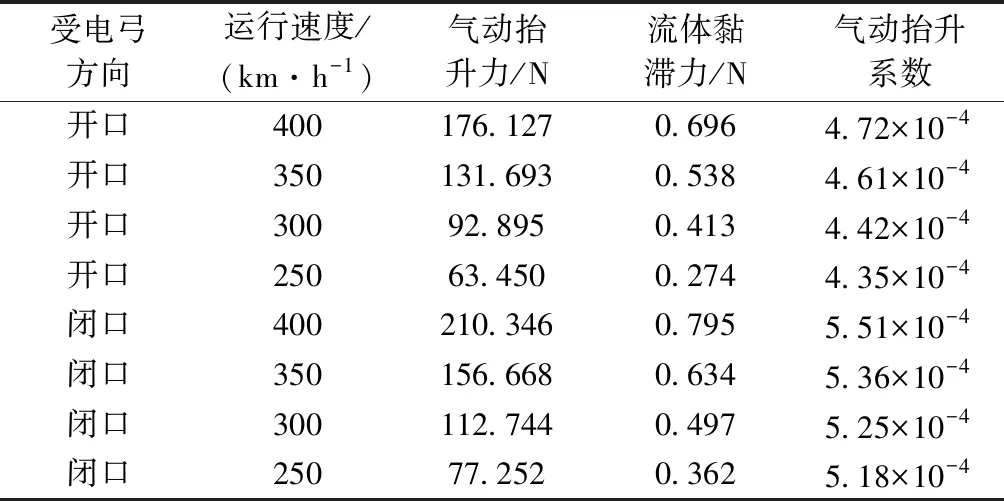
表1 仿真結(jié)果

由前文分析可知,氣動(dòng)抬升系數(shù)僅取決于受電弓本體幾何結(jié)構(gòu)和升弓高度(影響風(fēng)攻角)。當(dāng)本體幾何結(jié)構(gòu)既定時(shí),氣動(dòng)抬升系數(shù)與速度不產(chǎn)生關(guān)聯(lián)。但在實(shí)際中,由于氣動(dòng)黏性效應(yīng)速度提升會(huì)成使空氣邊界層密度降低,改變氣體相對受電弓表面的迎風(fēng)面積(略小于A′sinθ),而計(jì)算時(shí)將迎風(fēng)面積視為一個(gè)常量,因此氣動(dòng)抬升系數(shù)理論數(shù)值略大于實(shí)際數(shù)值。受電弓速度越高這種效應(yīng)越顯著。仿真結(jié)果亦受此影響,開口方向運(yùn)行的受電弓氣動(dòng)抬升系數(shù)為4.35×10-4～4.72×10-4,閉口方向?yàn)?.18×10-4～5.51×10-4。受電弓閉口方向運(yùn)行氣動(dòng)抬升力和氣動(dòng)抬升系數(shù)均大于開口方向。

2.3 不同升弓高度仿真結(jié)果

在前面研究的基礎(chǔ)上,考慮運(yùn)行速度不變的情況下,不同升弓高度對受電弓氣動(dòng)抬升系數(shù)的影響結(jié)果見圖5。

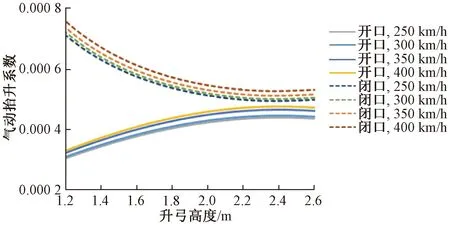
圖5 升弓高度與氣動(dòng)抬升系數(shù)關(guān)系

由圖5可見,仿真結(jié)果與前文理論分析結(jié)論相同。開口方向運(yùn)行的受電弓氣動(dòng)抬升系數(shù)隨升弓高度變大而增長,閉口方向反之。正常受電弓工作高度范圍內(nèi),受電弓閉口方向的空氣動(dòng)力性能低于開口方向。根據(jù)我國接觸線高度限界,升弓高度影響的氣動(dòng)抬升系數(shù)變化在10%以內(nèi)。

3 受電弓空氣動(dòng)力線路試驗(yàn)

為驗(yàn)證仿真計(jì)算結(jié)果和前文分析結(jié)論,通過線路試驗(yàn)測量實(shí)際運(yùn)行環(huán)境中受電弓的氣動(dòng)性能數(shù)據(jù)。線路試驗(yàn)的目的并非優(yōu)化或改進(jìn)已投入運(yùn)營的受電弓,而是用于與模型預(yù)測結(jié)果進(jìn)行對比,以驗(yàn)證仿真模型和前文的分析結(jié)論。

盡管風(fēng)洞試驗(yàn)在控制條件下易接近仿真條件,但線路試驗(yàn)可以更為準(zhǔn)確和真實(shí)地反映受電弓實(shí)際運(yùn)行情況,以提高模型預(yù)測的準(zhǔn)確性和實(shí)用性。故本文采用線路試驗(yàn)方式。

對國內(nèi)某線路采用250、300、350 km/h共3個(gè)速度級,在開、閉口兩個(gè)方向進(jìn)行空氣動(dòng)力線路試驗(yàn)。受電弓滑板的邊緣安裝4個(gè)壓力傳感器,用于測量受電弓上的空氣動(dòng)力,安裝方式見圖6。試驗(yàn)時(shí)令其中一個(gè)受電弓正常升弓受流,另一個(gè)受電弓升弓同時(shí)利用絕緣繩索控制其與接觸線保持150～200 mm的距離并通過壓力傳感器測量作用在弓頭處的空氣動(dòng)態(tài)力。測試完成后,打開絕緣繩索讓其升弓受流,并降下另一個(gè)受電弓進(jìn)行返程測驗(yàn),同時(shí)采集受流性能相關(guān)參數(shù),記錄測試結(jié)果。運(yùn)行工況如下:CRH3-013試驗(yàn)列車,K1587—K1799運(yùn)營區(qū)段,試驗(yàn)當(dāng)天天氣晴,無風(fēng),氣溫20 ℃。試驗(yàn)前,受電弓廠家對受電弓導(dǎo)流翼板進(jìn)行調(diào)整優(yōu)化,靜態(tài)抬升力設(shè)置為70 N。受電弓后弓開口方向在最高試驗(yàn)運(yùn)行速度時(shí)的弓網(wǎng)接觸力最大值為240～290 N,最小接觸力為40～90 N,氣動(dòng)抬升力為190～210 N;受電弓前弓閉口方向在最高試驗(yàn)速度運(yùn)行時(shí)的弓網(wǎng)接觸力最大值為260～320 N,最小接觸力為60～110 N,氣動(dòng)抬升力為215～235 N。弓網(wǎng)接觸力在相應(yīng)速度下的數(shù)值分布基本符合相關(guān)標(biāo)準(zhǔn),整個(gè)試驗(yàn)過程離線火花較小,無大的拉弧現(xiàn)象發(fā)生。

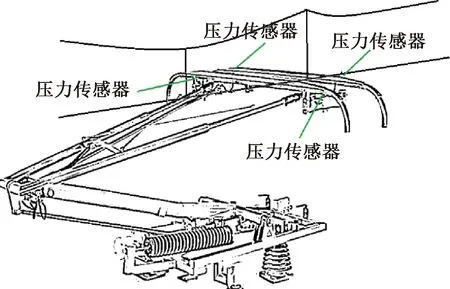
圖6 壓力傳感器安裝示意

傳感器連接監(jiān)控設(shè)備進(jìn)行實(shí)時(shí)測量,同時(shí)車頂安裝高速攝像機(jī)監(jiān)視受電弓運(yùn)行狀態(tài)。

對比線路試驗(yàn)數(shù)據(jù)和仿真結(jié)果,相對運(yùn)行速度的氣動(dòng)抬升力曲線對比見圖7。由圖7可見,試驗(yàn)測量數(shù)據(jù)與仿真結(jié)果基本吻合。

氣動(dòng)抬升系數(shù)的計(jì)算結(jié)果見表2,通過以下方法計(jì)算得出:在仿真軟件Fluent中,基于仿真模型計(jì)算得到迎風(fēng)面積A。在20 ℃、標(biāo)準(zhǔn)大氣壓下,空氣密度ρ為1.204 kg/m3。通過式(12)可得到氣動(dòng)抬升系數(shù)CL。試驗(yàn)中,氣動(dòng)抬升力為一個(gè)波動(dòng)區(qū)間,采用測量得到的統(tǒng)計(jì)平均值用同樣方法計(jì)算得出氣動(dòng)抬升系數(shù)。對比發(fā)現(xiàn)結(jié)果基本一致,最大相差約5%。

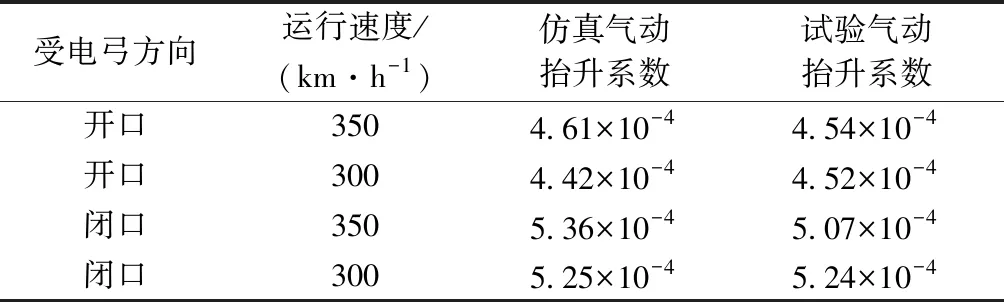
表2 氣動(dòng)抬升系數(shù)對比

4 結(jié)論

本文基于升弓高度的氣動(dòng)抬升系數(shù)和氣動(dòng)抬升力計(jì)算模型,對比仿真和線路試驗(yàn)結(jié)果分析,得到以下結(jié)論:

1)不考慮外界運(yùn)行環(huán)境時(shí),受電弓氣動(dòng)抬升力與列車運(yùn)行速度的平方和氣動(dòng)抬升系數(shù)成正比。受電弓本體幾何結(jié)構(gòu)既定條件下,可由升弓高度和開閉口方向計(jì)算受電弓氣動(dòng)抬升系數(shù),再基于列車運(yùn)行速度可求出氣動(dòng)抬升力。

2)受電弓在開口方向運(yùn)行時(shí)氣動(dòng)抬升系數(shù)、氣動(dòng)抬升力與升弓高度成正相關(guān)關(guān)系,在閉口方向運(yùn)行時(shí)呈負(fù)相關(guān)。不同升弓高度時(shí)氣動(dòng)抬升系數(shù)變化在5%～10%范圍內(nèi)。在升弓高度不變的情況下,開口方向氣動(dòng)抬升力和氣動(dòng)抬升系數(shù)小于閉口方向。仿真結(jié)果和線路測試數(shù)據(jù)均支持上述結(jié)論。為更全面地分析受電弓空氣動(dòng)力性能,應(yīng)考慮升弓高度對氣動(dòng)抬升力和氣動(dòng)抬升系數(shù)的影響。

氣動(dòng)抬升系數(shù)理論上是一個(gè)與速度不相關(guān)的常量,但在分析中發(fā)現(xiàn)在空氣黏性效應(yīng)作用下會(huì)隨速度提高發(fā)生些許變化。對速設(shè)為350 km/h及以下的受電弓影響不大,但未來進(jìn)一步提速時(shí)應(yīng)考慮受電弓高速情況下空氣流體密度變化、黏著性和可壓縮性等因素對氣動(dòng)抬升系數(shù)計(jì)算的影響。