考慮貨物異質性和模糊需求的高速鐵路貨運組織優化方法

陳婉茹，張得志，秦 進，曹 健，徐光明，王 超

(1.中南大學 交通運輸工程學院，湖南 長沙 410075；2.中國國家鐵路集團有限公司 辦公廳，北京 100044)

截至2021年底,我國高速鐵路(以下簡稱“高鐵”)運營里程突破4萬km,然而,部分線路部分時段的運力和設施能力在實際運營中未能充分利用。與此同時,公路快運正面臨著運能飽和和時效有限的雙重壓力[1]。2021年12月國務院頒布的《“十四五”現代綜合交通運輸體系發展規劃》中明確指出:利用“八縱八橫”的高鐵網提供的線路條件和穩定貨源[2],發揮高鐵在中長距離運輸方面成本低、容量大、速度快的突出優勢,發展高鐵快運等鐵路快捷貨運產品,是緩解公路運輸壓力,提升我國快捷貨物運輸效能的一大突破口[3]。然而,現階段基于客運捎帶和確認車運輸的高鐵快運干線組織模式存在節點功能不清晰、運輸效率低、集散能力不足等問題[4]。結合國外鐵路高速貨運產品的發展經驗,在夜間非天窗檢修時段開行高鐵貨運專列,是加強高鐵貨運能力建設的關鍵。

2020年高速貨運動車組就已下線,但其運輸組織方案至今仍未明確。為解決該問題,金偉等[5]研究高鐵快運組織方案優化問題,構建兩階段混合整數規劃模型并基于列生成算法求解。高如虎等[6]以時變需求為導向,按分階段優化的思路,研究快運專列時刻表和配裝方案的綜合優化方法。Hampaeyan等[7]以碳排放量最低為優化目標,構建混合整數非線性模型,確定城際單線雙向鐵路網中客貨列車運行的最佳調度計劃。Li等[8]在貨運專列和客車捎帶的組合服務模式下,以實現利潤最大化為目標,優化列車時刻表和貨物分配計劃。以上研究遵循“按流開車”的基本原則,對列車徑路、停站方案、開行頻率等高鐵貨運專列開行方案的部分內容進行了定量優化,但忽略了其與服務網絡和組織模式的相互關系,不利于指導生產實踐。

為逐步擴大高鐵貨運專列的運行范圍,穩步推進專列的成網開行,運輸組織需要考慮高鐵快運的網絡特征和產品供需特點。高鐵快運“軸-輻”式網絡見圖1,在高鐵快運網絡中,高鐵站點被劃分為一級樞紐和二級貨運站,二級貨運站依托高鐵經由一級樞紐彼此相連,具有“軸-輻”式特征[9]。為實現規模效應,降低單位運輸成本,二級貨運站的待運貨物依托一級樞紐間開行的高鐵貨運專列,實現由始發樞紐至貨運站的疏運或由貨運站至終到樞紐的集運,以直達或中轉的組織模式送至目的地所在高鐵站點[4]。除此之外,高鐵貨運專列的開行還應當考慮到如下現實特征:首先,受限于夜間的綜合維修天窗,能夠開行的專列數量有限;其次,高鐵貨運產品日益豐富,不再局限于單一快遞包裹,在運輸組織中需要考慮貨物的異質性;此外,快運需求具有不確定性,計劃需求和實際需求的差異將直接影響開行方案的服務質量。

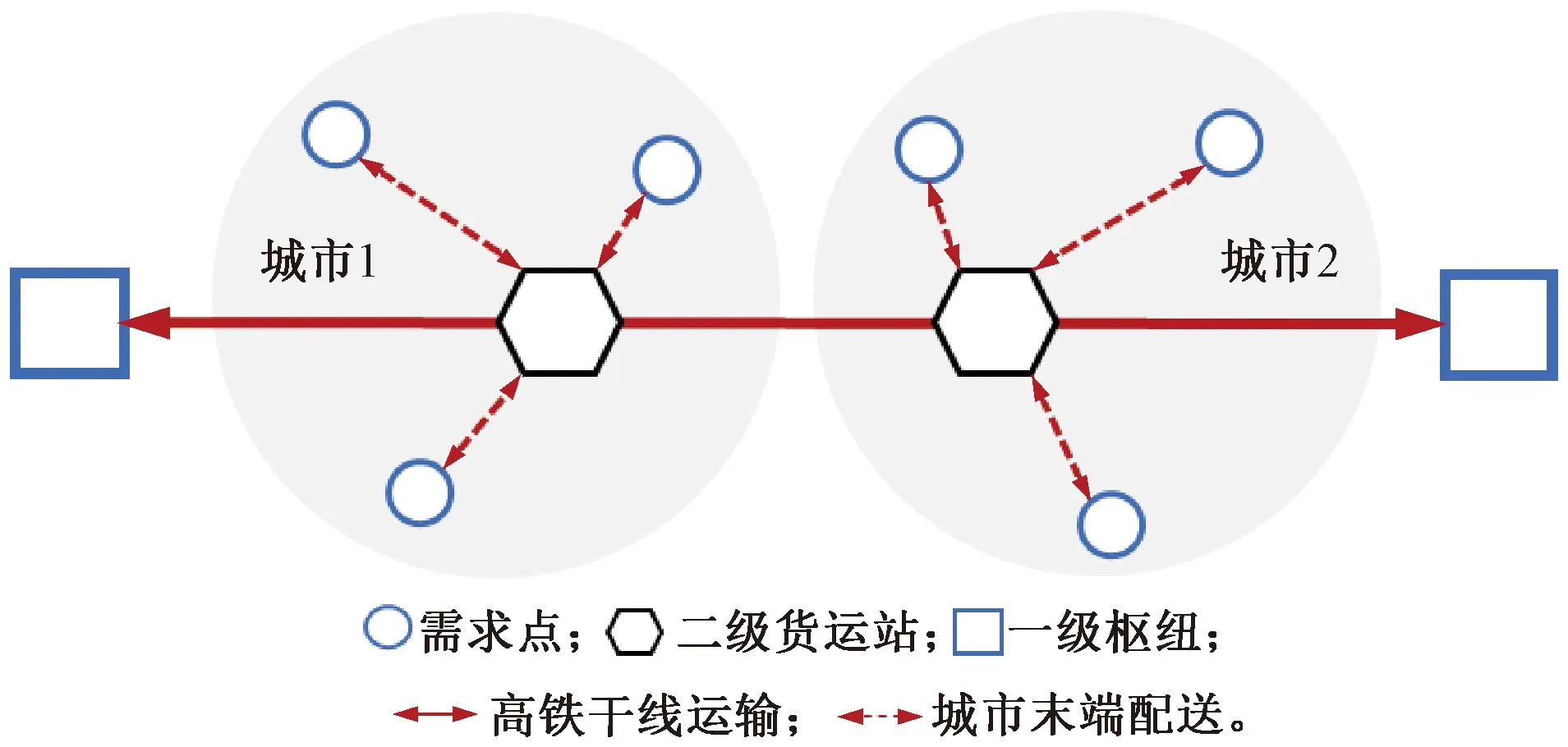
圖1 高鐵快運“軸-輻”式網絡

針對以上問題,本文面向高鐵“軸-輻”式快運網絡和高鐵快運貨物的集疏運需求,考慮高鐵快運需求的異質性和不確定性特點,提出基于裝載空間劃分和需求拆分的異質貨物協同運輸策略,引入模糊集貨需求下的機會約束,構建高鐵貨運專列開行方案和配載方案優化模型,設計并行改進變鄰域搜索算法求解。最后,以京滬高鐵貨運專列的開行為例,驗證上述模型和算法的有效性,探究決策者風險偏好對優化方案的影響,并給出相關建議。

1 模型構建

1.1 問題描述

本文基于“軸-輻”式網絡下快捷貨物的集疏運需求,研究單條高鐵線路某一方向貨運專列開行方案和配載方案的聯合優化問題。高鐵快運貨物的集疏運過程見圖2,V為高鐵線路站點集合,V={0,1,…,n,n+1},其中,0和n+1分別為始發和終到的一級樞紐,即所有列車均從樞紐0出發,最后返回樞紐n+1;N為線路途經二級貨運站集合N={1,…,n}。以一天為一個計劃期,K為線路在夜間非天窗檢修時段所能開行的有限專列集合,即線路通過能力為|K|對/天。貨物在一級樞紐和二級貨運站間的集疏運過程描述如下:高鐵貨運專列從一級樞紐站0出發,裝載OD為(0,i)的快運需求,將其運輸到車站i(1≤i≤n),即完成了快運貨物從起點至二級貨運站i的疏運;接著,到達車站j(i≤j≤n)裝載OD為(j,n+1)的快運需求,將其運輸到樞紐n+1,即完成了快運貨物從二級貨運站j至終點的集運。

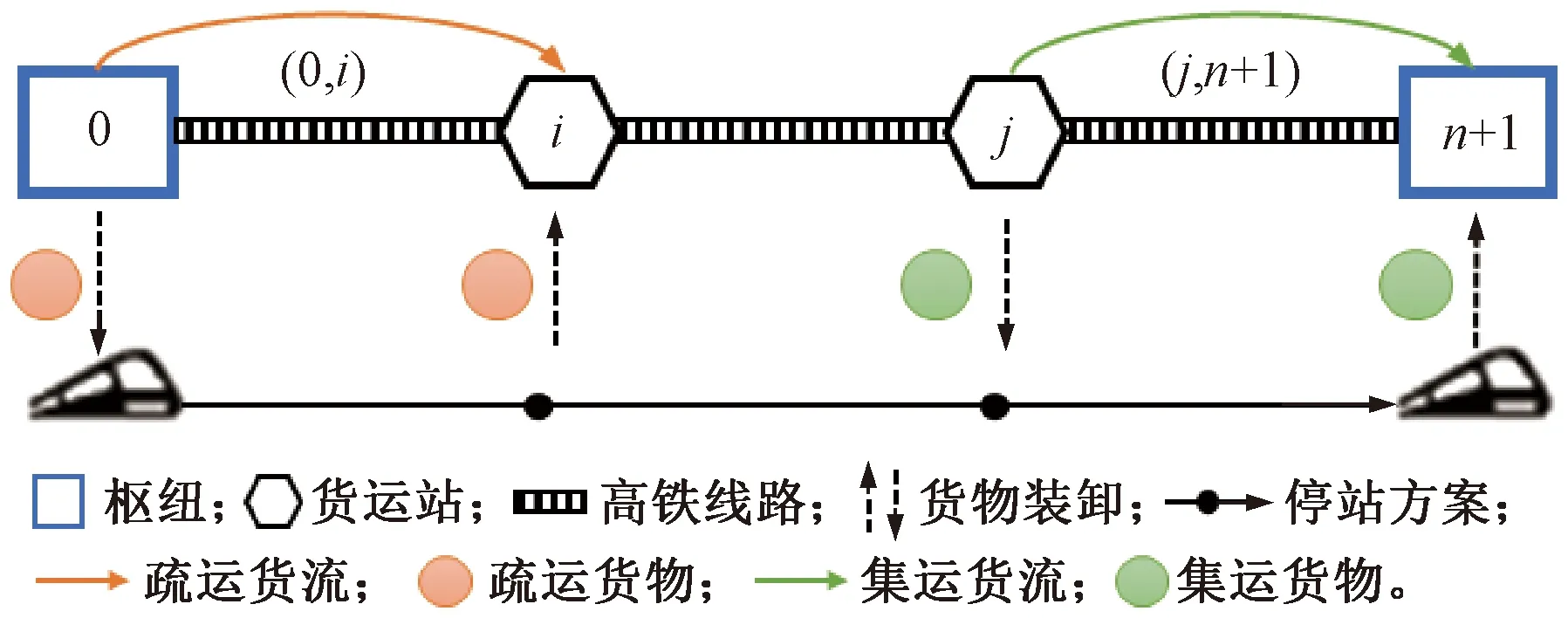
圖2 高鐵快運貨物的集疏運過程

基于以上分析,本文所研究的集疏運需求OD具備以下特點:疏運需求均以一級樞紐車站0為起點,集運需求均以一級樞紐車站n+1為終點。本文需要解決的問題是合理開行高鐵貨運專列,并將不同類貨物配載到不同專列上,滿足一級樞紐和各二級貨運站間的所有集疏運需求,具體內容包括優化高鐵貨運專列的開行對數、各高鐵貨運專列的停站方案及配載方案,使得總運營成本最低。

高鐵快運產品主要針對商務文件、電商包裹、數碼產品、生鮮等高附加值貨物。這些貨物對于運輸環境的要求不同,具有特殊屬性的貨物(例如藥品)不能與一般貨物混裝混運。但在已有研究中,貨物的異質性被忽略,相同OD的貨流被簡單合并。本文考慮將貨物依據相容性進行劃分,H為所有貨物種類構成集合,將列車內部空間劃分為|H|個與貨物種類一一對應的裝載空間,以實現異質貨物在空間上的分隔和時間上的同步運輸,高鐵貨運專列裝載空間劃分見圖3。值得注意的是,|H|是一個可以自定義的參數,可以根據具體的待運貨物進行設置,而對應的裝載空間可以根據貨物的種類數和需求量預先靈活劃分。當各二級貨運站的所有集疏運需求由唯一專列一次停站全部滿足時,所有專列共停站n次,可以最大限度減少停站作業成本。但異質貨物協同運輸時,不同裝載空間的容量相互制約,可能會造成運力虛糜。因此,將二級貨運站內的異質貨物需求拆分,并通過停站方案實現不同站點異質貨物需求的耦合,能夠更好地利用專列的裝載能力。

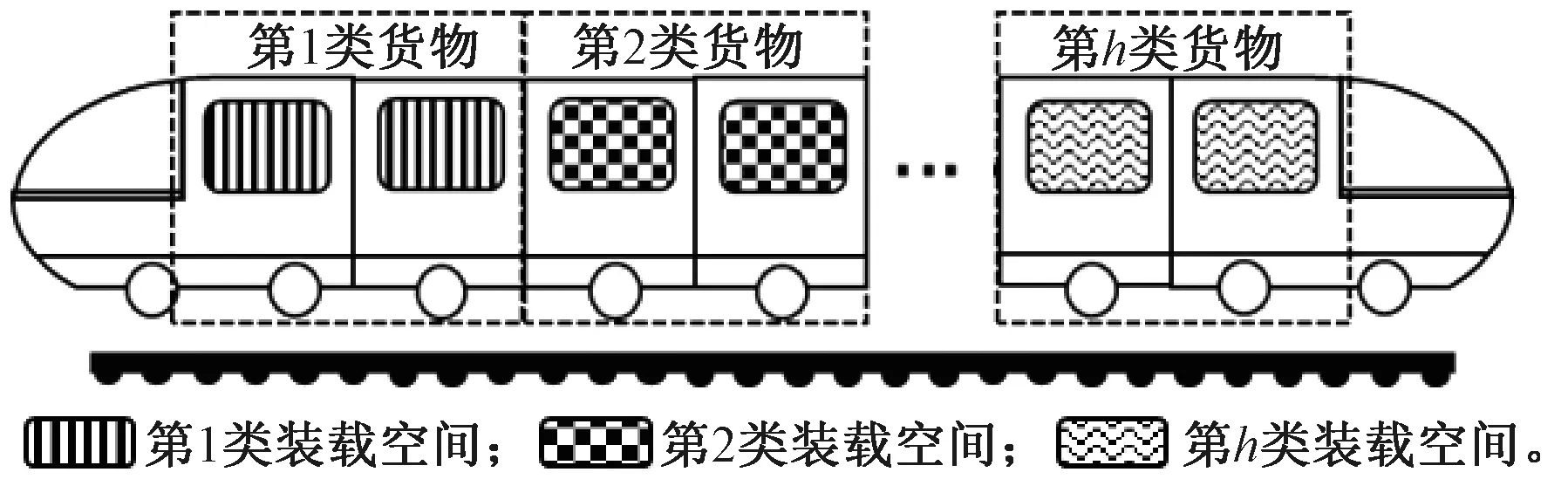
圖3 高鐵貨運專列裝載空間劃分示意

由于快運貨物具有小批量、多批次的特征,二級貨運站i∈N對h∈H類貨物的實際集運需求可能基于計劃集運需求波動[6],實際集運需求更趨向于一個模糊區間[10],在制定專列開行方案時應當考慮上述不確定需求[11]。相比于一般模糊集,三角模糊變量對快運需求模糊現象的描述更為貼切[10],因此采用三角模糊變量描述集貨需求的不確定性。不失一般性,將實際集運需求設定為對稱三角模糊數[12],即

式中:pih為集運需求的期望;Lpih、Mpih分別為實際集運需求的下界和上界,且有Lpih=(1-?)pih,Upih=(1+?)pih,?為集運需求的波動因子。

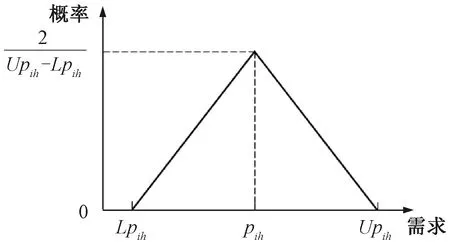
圖4 模糊集運需求的概率密度函數

做出如下基本假設:

1)開行的有限專列能夠滿足線路上所有二級貨運站的集疏運需求。

2)所有二級貨運站的各類貨物集疏運需求均不超過對應裝載空間容量,可以被一次滿足。

3)二級貨運站內的不同類貨物集疏運需求可拆分,并由不同專列滿足;同類貨物集疏運需求不可拆分,需由唯一專列一次滿足。

4)僅以重量衡量專列的載運能力,不考慮貨物體積對裝載的影響,且貨物運輸過程中不允許混裝。

決策變量見表1。

表1 決策變量

1.2 優化模型

模型以高鐵快運專列的總運營成本最低作為優化目標,包括固定成本、變動成本和停站成本。固定成本由專列開行數量決定,變動成本由專列的走行距離決定,停站作業成本由專列停站作業次數決定,即

( 1 )

式中:c1為專列開行的單位固定成本;c2為專列在區間行駛單位距離的平均開行成本;c3為專列的單位停站服務成本;r為始發終到樞紐間的線路里程。

1) 集疏運需求約束

所有集疏運需求都將被唯一服務,即

( 2 )

2) 停站約束

停站約束為

( 3 )

( 4 )

( 5 )

式中:M為一個足夠大的正數。

式( 3 )表示當前專列不開行時,在任何途經站點都不停站。式( 4 )、式( 5 )保證專列停站時一定服務于站點的需求。

3) 載貨能力約束

式( 6 )限制發車時各裝載空間的裝載量不超過其裝載能力。

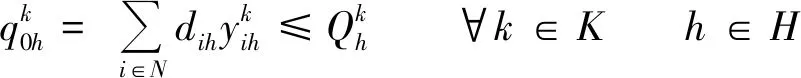
( 6 )

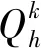
專列在途的貨流量守恒約束為

?i∈Nk∈Kh∈H

( 7 )

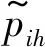
引入決策者的風險偏好值α,α∈[0,1],但一般不取0值,故有α∈(0,1][10]。限制專列服務完任意站點后各裝載空間載重小于其裝載能力的概率需大于等于預先設定的決策者風險偏好值α,即

( 8 )

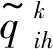
( 9 )

4)決策變量取值約束

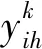
xk={0,1}k∈K

(10)

(11)

專列的載貨量滿足非負約束

(12)

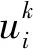
2 求解算法

2.1 算法框架

構建的非線性混合整數規劃模型,涉及多個多維決策變量,其組合數隨著問題規模的增大將爆炸式增長,屬于NP難問題。為了實現模型的高效求解,本文設計了基于并行改進變鄰域搜索(Parallel Improved Variable Neighborhood Search, PIVNS)的啟發式算法,總體框架見圖5。

PIVNS算法基于3步后悔值插入算法[13]得到初始解;通過均衡擾動策略擴大搜索范圍;采用變鄰域下降[14]策略在給定鄰域結構內嵌套尋優;達到最大迭代次數或最大不改進迭代次數時算法終止。

2.2 評價函數

對?i∈N,h∈H,順序編碼站點i的h類貨物需求,構成需求集合R={r1,r2,…,r|N|×|H|}。構造|K|個與專列一一對應的空數組,記錄其服務需求和服務順序。將?ri∈R,i=1,2,…,|N|×|H|唯一指配給一列專列即構成一個解x。然而,并非所有解都能夠滿足載重約束,在評價解時需要對載重約束的違反施加懲罰,促使搜索朝著可行域的方向收斂[15]。因此,本文設計評價函數為

F(x)=f(x)+γiV1(x)+δiV2(x)

(13)

式中:f(x)為由式( 1 )計算得到的總成本;V1(x)和V2(x)分別為當前解中載重約束式( 6 )和式( 8 )的違背量;γi,δi為動態懲罰因子。若在第i-1次迭代后得到的局部最優解不違反約束式( 6 ),則在第i次迭代時置γi為γi-1的1/ρ倍,否則置其為γi-1的σ倍。同理,根據第i-1次迭代后得到的局部最優解是否違反約束式( 8 )更新δi。

2.3 初始解

基于3步后悔值插入[13]的方法生成初始解:對?ri∈R計算3步后悔值R3(ri);以最佳服務順序將argmax{R3(ri),ri∈R}指派給使得評價函數值最少增加的專列,最佳服務順序指需求點插入當前專列對應數組時引起評價函數值增加最少的位置;更新R=R{ri};重復以上步驟直到R=?。需求點ri的3步后悔值為

(14)

式中:fi,k為將需求ri以最佳的服務順序指派給專列k所帶來的評價函數值增量;xij為專列序號,當需求ri以最佳服務順序指派給該專列時,評價函數值增量相較于指派其他專列是第j小的。

2.4 VNS算法

1)鄰域結構

VNS算法涉及的鄰域結構由如下算子產生:

inter-swap (n-n-n):如圖6所示,該算子用以順序交換三列專列所服務的連續n個需求點。

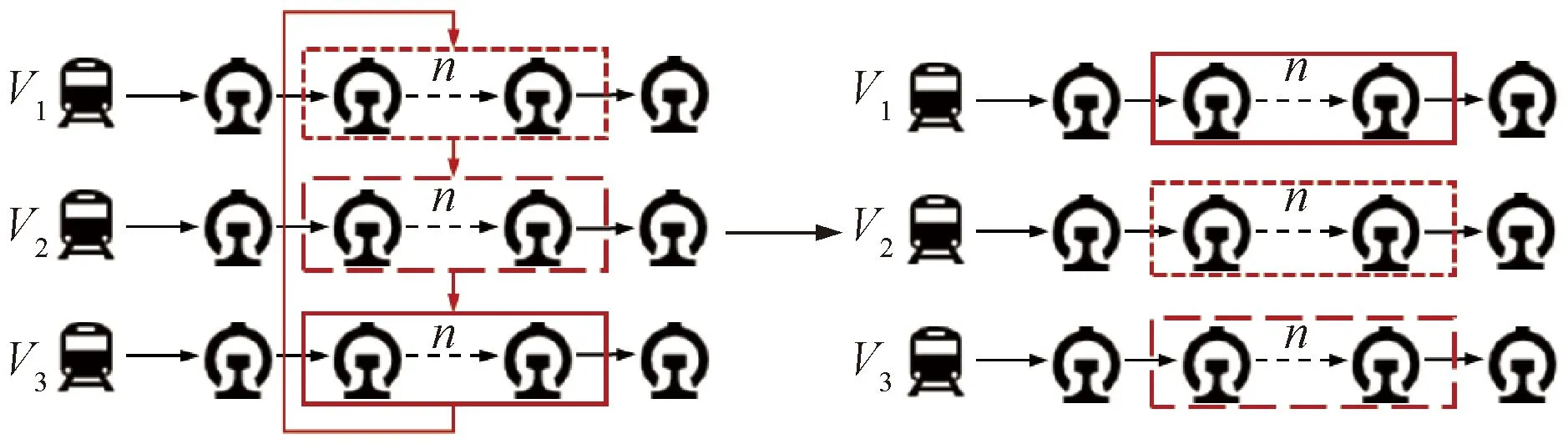
圖6 inter-swap (n-n-n)算子示意

1-insert:將一列專列所服務的一個需求點重新指派給另一專列。

2-insert:將一列專列所服務的連續兩個需求點重新指派給另一專列。

Inter swap 1-1:交換一列專列所服務的一個需求點與另一專列所服務的一個需求點。

Inter swap 2-2:交換一列專列所服務的連續兩個需求點與另一專列所服務的連續兩個需求點。

Intra 2-opt:將一列專列所服務的連續兩個需求點以不同的服務順序重新指派給當前專列。

Intra swap:交換一列專列所服務的兩個需求點的服務順序。

Shift:將一列專列所服務的一個需求點以不同的服務順序重新指派給當前專列。

2)擾動

為了擴大搜索范圍,需要擾動當前解,即從定義的鄰域結構中選擇一個解輸入局部搜索。3個擾動鄰域結構基于算子inter-swap (n-n-n)產生。不妨設C1,C2,C3分別為三列專列所服務需求的數量,表2給出鄰域結構κ對應的算子最大操作長度nmax。nmax的設置在保證n不超過擾動路徑長度的同時,給出n的上界。鄰域中n的取值是隨機的。

表2 抖動鄰域結構

3)局部搜索

局部搜索指在給定鄰域結構NK(x)內搜索改進解以更新當前解的過程。7個局部搜索鄰域結構由算子1-insert,2-insert,Inter swap 1-1,Inter swap 2-2,Intra 2-opt,Intra swap,Shift依次生成。研究表明,最佳改進搜索策略能更好地平衡算法的求解質量和運行時間[16]。設當前解x的鄰域結構NK(x)中包含解x1,…,xn,xi=F(xi)-F(x)。若xi≥0,?xi∈NK(x),則不更新當前解x;否則以argmin{xi,xi∈NK(x)}更新x。若在鄰域結構NK(x)中更新當前解,則搜索回到鄰域N1;否則搜索鄰域NK+1。當K>7時,本次迭代中的局部搜索結束。

2.5 IVNS算法

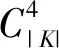
2.6 PIVNS算法

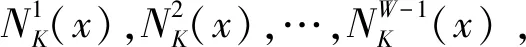
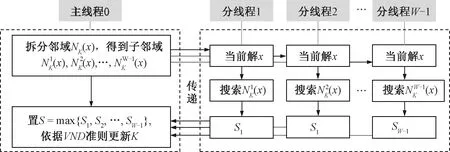
圖7 并行局部搜索示意

3 算例仿真與分析

3.1 算例設計及參數

本文以京滬高鐵為例進行仿真分析,線路示意見圖8。

圖8 京滬線高速鐵路線路示意

假定線路的專列通過能力為6對/d[18],|H|=2且兩類貨物需求相當,8節編組專列被均分為兩個由4

節車廂組成的裝載空間,單節車廂最大載重為143.75 kN。單位固定成本c1為42萬元/列,單位可變成本c2為0.07萬元/km,單位停站成本c3為5萬元/次[5]。二級貨運站i∈N對h∈H類貨物集疏運需求pih、dih見表3。設置算法最大迭代次數和最大不改進迭代次數分別為2 000和150,動態懲罰因子控制參數ρ,σ均為100。所有算法通過Matlab 2020a編程實現,計算機參數配置為Intel Core i5-9500,3.0 GHz,8 GB RAM。各算例下算法的測試結果均基于10次運算。

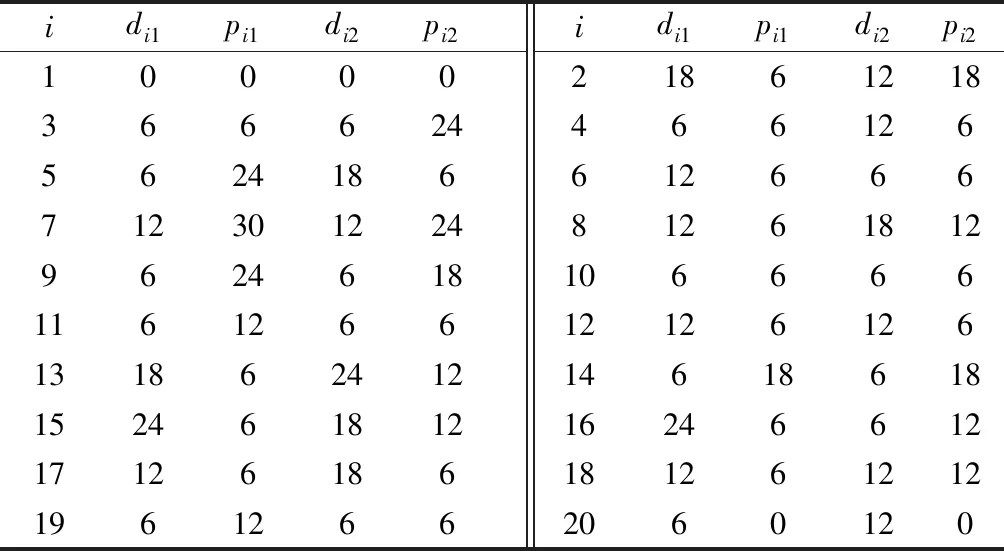
表3 算例詳細信息表

3.2 算法對比分析

當?=0.25時,對比VNS算法、IVNS算法和PIVNS算法在偏好值α∈(0,1]按0.1增時的求解結果,以驗證PIVNS算法的有效性和穩定性。表4給出各算法求得的最優解Bbest、平均值Aavg、平均值Aavg相對于Bbest的誤差比率Ggap和與Bbest對應的最佳運行時間T。

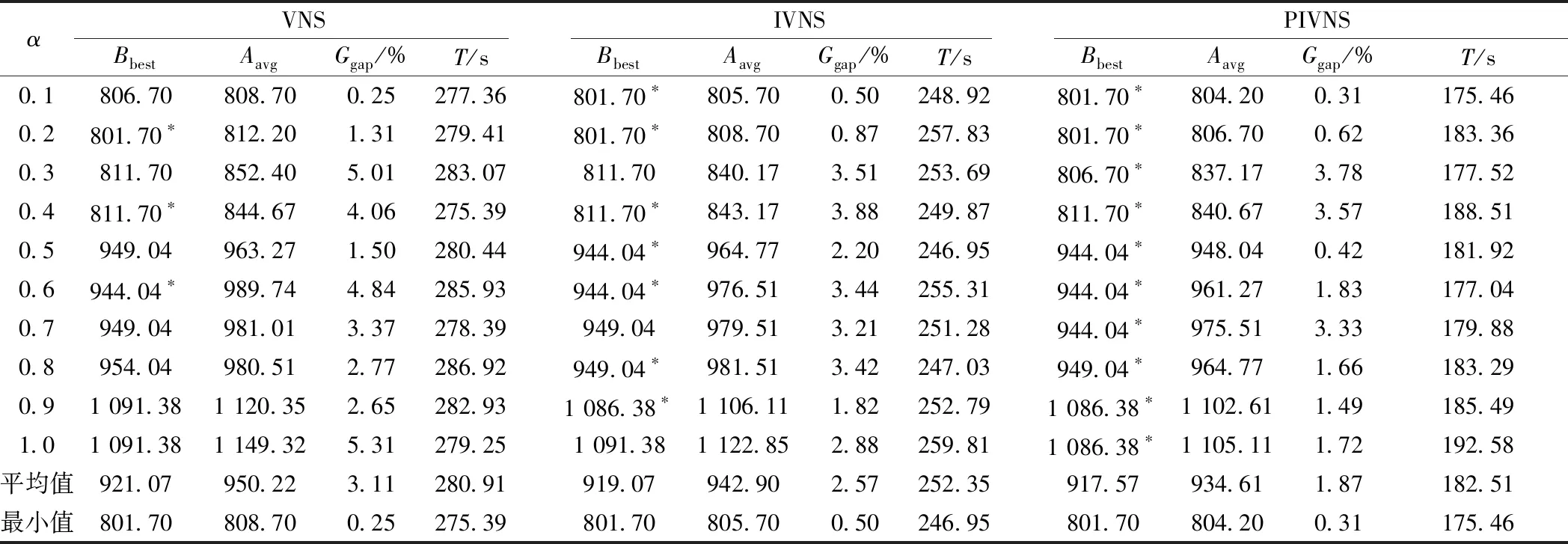
表4 PIVNS算法和VNS算法、IVNS算法的求解結果對比

Ggap=(Aavg-Bbest)/Bbest×100%

(15)

由表4可知,PIVNS算法求得所有偏好值下的當前最優解,IVNS算法求得其中7個,VNS算法僅求得3個,說明改進策略的加入能增強算法的全局搜索能力,一定程度上避免算法陷入局部最優;在求解時間方面,PIVNS算法的計算時間均要明顯少于VNS算法和IVNS算法,說明并行策略的加入能大大提升算法的運行的效率;在求解穩定性方面,VNS的算法的平均Ggap為3.11%,IVNS算法的平均Ggap為2.57%,PIVNS算法的平均Ggap最小,僅為1.87%,說明PIVNS算法的求解較為穩定。

3.3 結果分析

基于提出的PIVNS算法,對比分析?=0、?=0.25且偏好值α∈(0,1]按0.1遞增時不同運輸策略下的優化方案。其中,MCSD為裝載空間劃分且需求拆分策略,MC為裝載空間劃分但需求不拆分策略,SC為不劃分裝載空間且需求不拆分策略。SC策略中始發站配備分別用于運輸兩類貨物的專列各|K|/2列。當前偏好值下各策略組織方案總成本Bbest和當前策略Bbest相對于MCSD策略的誤差比率Ggap見表5。

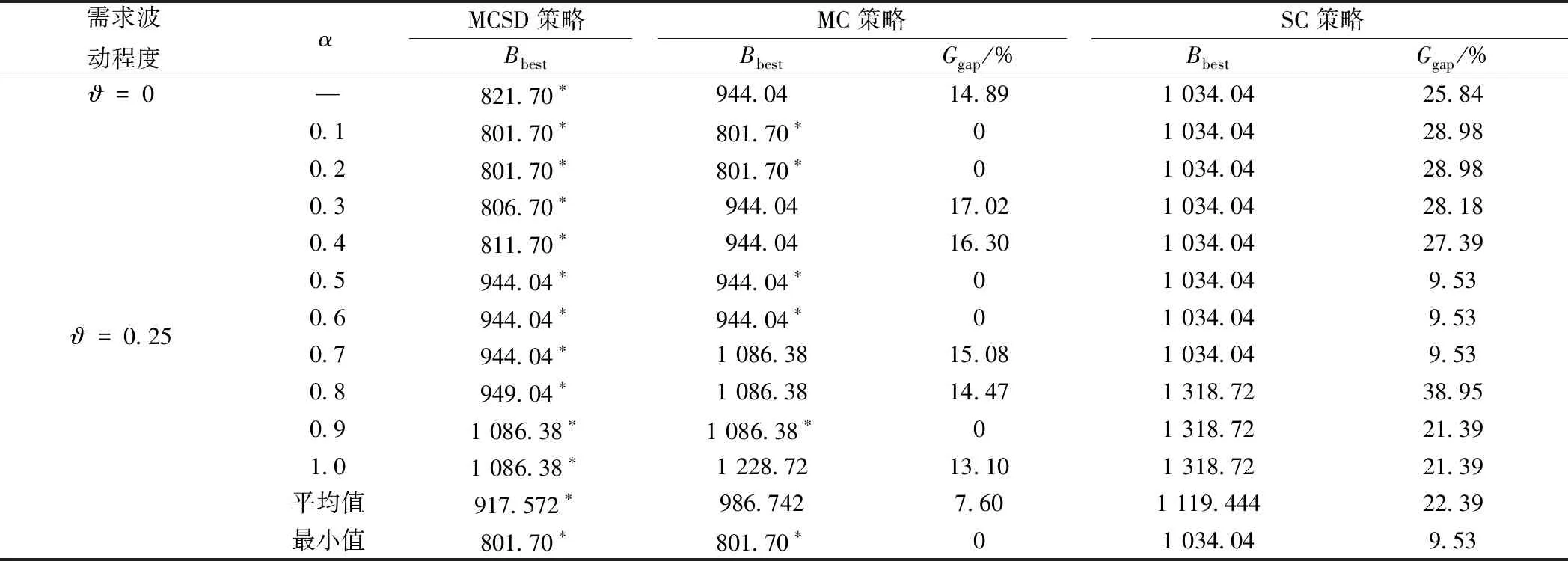
表5 不同波動因子下不同策略的求解結果

(16)

1)異質物協同配送策略

?=0時各策略優化方案見圖9。在開行對數方面,SC策略和MC策略的開行對數均為6列,而MCSD策略為5列。在停站方案方面,MC策略停站次數最少,MCSD策略次之,SC策略停站次數最多。相較于MC策略,MCSD策略通過犧牲部分停站成本實現了固定成本和變動成本的大幅下降。為了更加直觀地對比不同運輸策略下配載方案的優劣,表6給出各策略方案的區間平均裝載率,裝載率為實際載貨量和專列最大裝載能力的比值。

圖9 ?=0時各策略下的優化方案

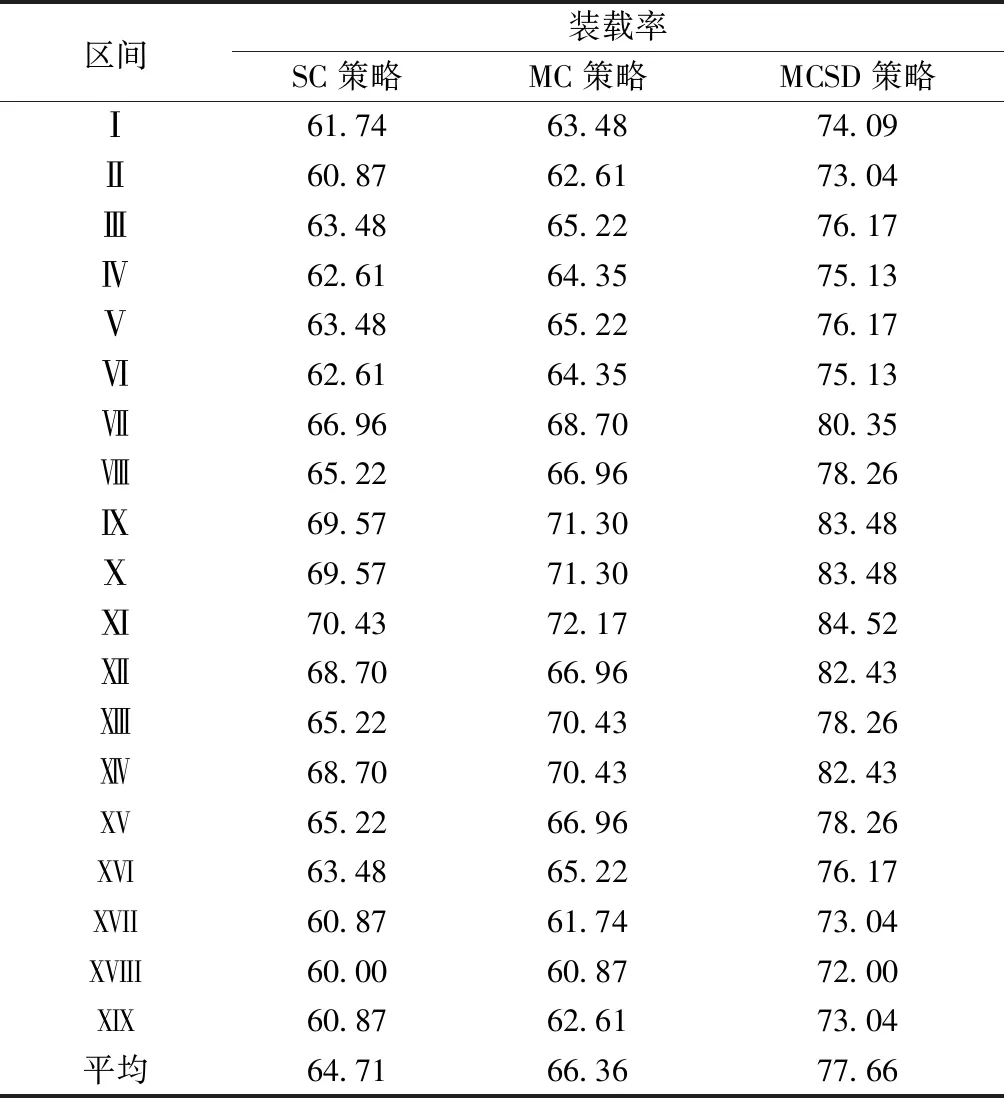
表6 各策略下確定模型優化方案的區間裝載率 %

由表6可知,高鐵貨運專列的在途載貨量是動態變化的。在裝載空間容量約束下,為滿足全部集疏運需求,SC策略中V2和V4專列的運力大量虛糜,平均區間裝載率為64.71%。MC策略中不同裝載空間的容量互相制約同樣導致V5和V6專列的運力大量虛糜,平均區間裝載率為66.36%。多類貨物協同運輸的MCSD策略能夠優化整體方案,平均區間裝載率為77.66%。

2)模糊需求下決策者偏好的影響

α的大小反應決策者在模糊環境下對待風險的態度。α越小,決策者越冒險,希望當前專列可以服務更多需求,而服務失敗的概率也越大,會對客戶滿意度造成負面影響;α越大,決策者越保守,更重視線路可行性安排,雖然服務失敗的風險低,但會導致運力資源浪費。需要注意的是,專列可服務的需求點數量受到配貨需求的硬性約束,并不會隨著偏好的減小而一直增加。

偏好值的設置可以參考?=0時的求解結果,即確定計劃需求下的運輸組織方案。在當前算例中,當α取0.5～0.7時,既不會因為決策者的保守而帶來較大的浪費,也預留了部分運力用以滿足波動的集貨需求,是較為合適的。此外,動態設置偏好值能夠有效規避固定偏好值設置不合理而導致的問題,即在不同周期的決策內,根據當前貨物的實際波動情況,設置不同的偏好值,以更好地安排運力。

4 結論

本文針對需求不確定的異質快運貨物在高鐵貨運“軸-輻”式網絡中的集疏組織問題,研究高鐵貨運專列開行方案和配載方案的聯合優化方法。以運營成本最低為優化目標,構建基于模糊需求的混合整數非線性規劃模型,設計并行改進變鄰域搜索(PIVNS)算法進行求解。以京滬高速鐵路為背景的仿真實驗結果表明:

1)PIVNS算法的求解有效且穩定,提出的均衡擾動策略能夠增強算法的全局搜索能力,采用的并行局部搜索策略能夠減少算法運行時間。

2)基于專列裝載空間劃分和站點需求拆分的異質貨物協同運輸策略能夠優化方案的開行對數,合理安排列車停站,有效提高專列在區間的裝載率,降低配送成本。

3)決策者對待模糊需求的風險偏好會直接影響組織方案,偏好值的設置應當以確定計劃需求下的組織方案為基準,并結合貨物需求的實際波動情況,在不同計劃周期內動態設置。

本文的研究為相關部門實現高鐵干線集疏運的智能組織調度提供有力支撐。未來的研究將圍繞提高算法效率及多組織模式下高鐵快運專列的成網運行展開。