C、Mn對(duì)γ-Fe層錯(cuò)能影響的第一性原理研究

蔣人豪 盧冠杰 董 瀚 史 文 王 洋

（1.上海大學(xué) 材料科學(xué)與工程學(xué)院，上海 200444；2.上海大學(xué) 計(jì)算機(jī)工程與科學(xué)學(xué)院，上海 200444）

先進(jìn)高強(qiáng)鋼因具有良好的力學(xué)性能而被廣泛應(yīng)用于眾多領(lǐng)域［1-3］。其優(yōu)異的力學(xué)性能主要來(lái)源于變形過(guò)程中奧氏體發(fā)生的相變誘導(dǎo)塑性（transformation induced plasticity，TRIP）和／或?qū)\晶誘導(dǎo)塑性（twinning induced plasticity，TWIP）效應(yīng)［4］。這兩種變形機(jī)制都是提高材料強(qiáng)韌性的重要手段，不同之處在于TRIP效應(yīng)是鋼在變形過(guò)程中亞穩(wěn)奧氏體經(jīng)歷γ →ε →α′相變或γ →ε 相變［4］，使材料的強(qiáng)度和塑性得到提高，而TWIP效應(yīng)則是在變形過(guò)程中出現(xiàn)孿晶組織，使材料的強(qiáng)韌性得到改善［5］。層錯(cuò)能（stacking fault energy，SFE）是決定材料變形機(jī)制的重要因素之一［6］。層錯(cuò)能小于18 mJ／m2，相變是主要的變形機(jī)制；層錯(cuò)能介于12 ～35 mJ／m2之間，孿晶是主要的變形機(jī)制；層錯(cuò)能大于35 mJ／m2，滑移占主導(dǎo)［7-10］。層錯(cuò)能是一種原子尺度的性能［8］，試驗(yàn)中任何一個(gè)細(xì)微的變化都將影響層錯(cuò)能的準(zhǔn)確度，而采用理論計(jì)算可準(zhǔn)確獲得各元素對(duì)層錯(cuò)能的影響。C、Mn是先進(jìn)高強(qiáng)鋼中的重要元素［11-12］，對(duì)層錯(cuò)能具有重要影響，故本文通過(guò)第一性原理計(jì)算研究了C、Mn 對(duì)γ-Fe 層錯(cuò)能的影響，并以形成層錯(cuò)后的自由能ESF為依據(jù)確定C、Mn 在γ-Fe 中的最穩(wěn)定位點(diǎn)，計(jì)算和預(yù)測(cè)了相應(yīng)的層錯(cuò)能和變形機(jī)制。

1 理論方法

層錯(cuò)是金屬中常見(jiàn)的晶體缺陷，由正常堆垛的原子層出現(xiàn)錯(cuò)排而引起。在面心立方（face center cubic，F(xiàn)CC）金屬的密排面上，原子的正常堆垛順序從... ABCABCABC... 轉(zhuǎn)變?yōu)?..ABCABC ｜BCABC...時(shí)，就形成了一個(gè)內(nèi)廩層錯(cuò)，層錯(cuò)區(qū)域變?yōu)镠CP（hexagonal close packed）結(jié)構(gòu)。“｜”代表層錯(cuò)所在位置。γSF表示層錯(cuò)能，表達(dá)式為，其含義為自由能之差與層錯(cuò)面積之比。Gdef、Gfcc、A分別代表形成缺陷時(shí)的自由能、完美排列晶體的自由能以及層錯(cuò)面積。本文采用Bleskov等［13］提出的層錯(cuò)模型，由FCC 晶胞經(jīng)過(guò)切面得到，如圖1 所示。層錯(cuò)模型有12層，每層2 個(gè)原子。圖1 中紅色虛線為層錯(cuò)面，層錯(cuò)面上半部分方向進(jìn)行剪切。位移量為時(shí)，會(huì)形成一個(gè)勢(shì)壘USF（unstable stacking fault），對(duì)應(yīng)的層錯(cuò)能為γUSF，γUSF越大，變形需要克服的勢(shì)壘越大。位移量為時(shí)，在層錯(cuò)面附近形成ε 相（intrinsic stacking fault，ISF結(jié)構(gòu)），如圖1（e）綠框所示。ISF 結(jié)構(gòu)對(duì)應(yīng)的層錯(cuò)能為內(nèi)廩層錯(cuò)能（intrinsic stacking fault energy，ISFE），即γISF。γISF＞0，代表形成缺陷時(shí)體系自由能高于FCC 晶體，F(xiàn)CC 相更穩(wěn)定，不會(huì)發(fā)生γ→ε轉(zhuǎn)變；γISF＜0，容易發(fā)生γ→ε轉(zhuǎn)變。在形成ISF 結(jié)構(gòu)后，將圖1（e）藍(lán)框內(nèi)的原子進(jìn)行“二次剪切”，可獲得孿晶（twin stacking fault，TSF結(jié)構(gòu)），剪切時(shí)存在兩個(gè)特殊值，分別為γUTF孿晶勢(shì)壘與γTSF孿晶缺陷能［14］。

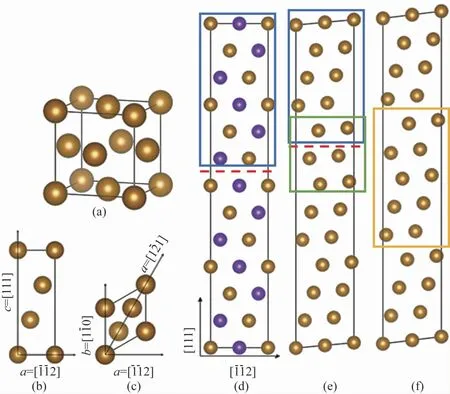
圖1 構(gòu)建層錯(cuò)模型示意圖（（a）FCC晶胞；（b）切面后晶胞的側(cè)視圖；（c）切面后晶胞的俯視圖；（d）擴(kuò)胞后的層錯(cuò)模型，黃色原子磁序?yàn)檎仙哟判驗(yàn)樨?fù)；（e）ISF結(jié)構(gòu)，藍(lán)框內(nèi)為ε相；（f）TSF結(jié)構(gòu)，黃框內(nèi)為孿晶）Fig.1 Schematic diagrams of building a stacking fault model（（a）FCC unit cell；（b）side view of the unit cell after sectioning；（c）top view of the unit cell after sectioning；（d）stacking fault model obtained by cell expansion，where yellow atoms represent positive magnetic order，and purple atoms represent negative magnetic order；（e）ISF structure，ε phase in the blue box；（f）TSF structure，twinning in the yellow box）

本文通過(guò)Jo 等［15］的塑性理論，由γd值判斷層錯(cuò)、孿晶、滑移傾向，表達(dá)式為

式中：－0.5 ＜γd＜0 時(shí)，層錯(cuò)與滑移共存，但層錯(cuò)占主導(dǎo)；0 ＜γd＜2 時(shí)，孿晶與滑移共存，且γd越小，孿晶的比例越高；γd＞2 時(shí)，僅存在滑移。

此外，理想狀態(tài)下FCC 金屬的孿晶形成能力可通過(guò)固有孿晶判據(jù)P來(lái)判斷［16］，P越大說(shuō)明孿晶能力越強(qiáng)，表達(dá)式為：

孿晶形成的另一個(gè)重要因素是臨界孿晶應(yīng)力。臨界孿晶應(yīng)力τcrit的值越小，說(shuō)明孿晶越易形成。Kibey等［17］提出了FCC 金屬臨界孿生應(yīng)力的表達(dá)式，如下：

所有計(jì)算通過(guò)Vienna Ab-initio Simulation Package（VASP）軟件包實(shí)現(xiàn)［18-19］。離子-電子間的相互作用采用綴加投影波贗勢(shì)方法來(lái)描述（projected augmented wave，PAW），交換關(guān)聯(lián)效應(yīng)通過(guò)廣義梯度近似框架（generalized gradient approximation，GGA）下的PW91 進(jìn)行處理［20］。經(jīng)過(guò)收斂性測(cè)試后確定平面波截?cái)嗄転?50 eV。布里淵區(qū)的積分采用Monkhorst-Pack特殊k點(diǎn)網(wǎng)格方法，經(jīng)過(guò)收斂性測(cè)試后確定k 點(diǎn)為7 ×15 ×1。計(jì)算時(shí)的收斂標(biāo)準(zhǔn)為10－4eV。

2 結(jié)果與討論

2.1 γ-Fe的層錯(cuò)能

主要對(duì)無(wú)磁（non-magnetic，NM）和反鐵磁（antiferromagnetic，AFM）態(tài)γ-Fe 的層錯(cuò)能進(jìn)行計(jì)算。γ-Fe面心立方模型經(jīng)弛豫后得到NM態(tài)的晶格常數(shù)為3.45 ?，而AFM態(tài)的為a ＝b ＝3.41 ?，c／a ＝1.07，與文獻(xiàn)中的弛豫結(jié)果一致［21］。弛豫后的晶胞經(jīng)切面得到層錯(cuò)模型，其廣義層錯(cuò)能（generalized stacking fault energy，GSFE）如圖2 所示。由圖2 可知，隨著剪切運(yùn)動(dòng)的位移量增大，NM與AFM態(tài)γ-Fe的GSFE均呈現(xiàn)出先上升后下降的趨勢(shì)，前半段的上升表明勢(shì)壘的形成，隨后的下降表明開始形成內(nèi)廩層錯(cuò)。層錯(cuò)能的計(jì)算結(jié)果如表1 所示。NM 態(tài)γ-Fe 的γUSF與γISF分別為478、－400 mJ／m2，與Medvedeva 等［22］的結(jié)果比較接近，而AFM態(tài)γ-Fe的γUSF與γISF分別為239、122 mJ／m2，與Cui 等［23］的計(jì)算結(jié)果較為接近。這說(shuō)明本文設(shè)置的計(jì)算參數(shù)具有相當(dāng)?shù)目煽啃浴淖杂赡艿慕嵌瓤紤]，NM態(tài)γ-Fe 發(fā)生剪切運(yùn)動(dòng)后傾向于形成具有HCP 結(jié)構(gòu)的ε 相。但引入磁性后，層錯(cuò)能由負(fù)轉(zhuǎn)為正，ε 相不容易產(chǎn)生。實(shí)際奧氏體為順磁性，凈磁矩為0，而反鐵磁性的凈磁矩也為0，故采用反鐵磁的計(jì)算結(jié)果更接近實(shí)際。同樣后續(xù)計(jì)算的磁性也設(shè)置為反鐵磁。

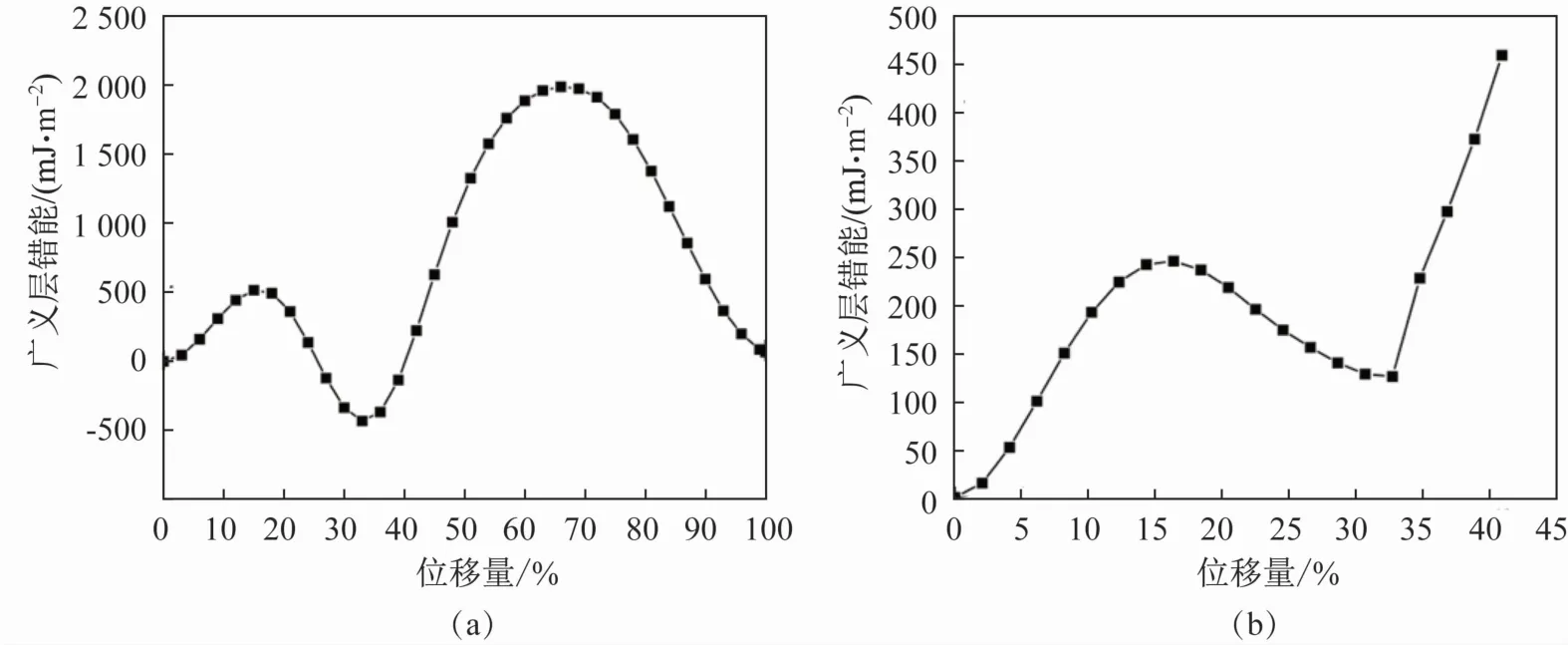
圖2 NM（a）與AFM態(tài)（b）γ-Fe的廣義層錯(cuò)能曲線Fig.2 Generalized stacking fault energy curves of γ-Fe in NM and AFM states

2.2 C、Mn對(duì)γ-Fe層錯(cuò)能的影響

C是間隙原子，位于層錯(cuò)模型的八面體間隙位置；Mn 是置換性原子，通過(guò)替換層錯(cuò)模型中的Fe進(jìn)入模型。將合金原子與層錯(cuò)面的距離定義為n（n ＝0，1，2，3），其中n ＝0 表示合金原子位于層錯(cuò)面上，n ＝1，2，3 則表示該合金原子位于層錯(cuò)面下方且距離層錯(cuò)面1，2，3 個(gè)原子層處。具體原子位置示意圖如圖3 所示。

表2 為Fe24C1 模型中C 與層錯(cuò)面之間的距離不同時(shí)計(jì)算得到的γUSF和γISF，圖4 為4 個(gè)不同C位點(diǎn)的GSFE曲線。由圖4 可知，n ＝0 位點(diǎn)的GSFE曲線變化趨勢(shì)與其他3 個(gè)位點(diǎn)的趨勢(shì)不同。n ＝0 位點(diǎn)的C正好位于層錯(cuò)面上，當(dāng)位移量達(dá)到時(shí)，層錯(cuò)面上方的Fe正好處在C的正上方，在層錯(cuò)區(qū)域形成了一種不穩(wěn)定結(jié)構(gòu)，在圖中則表現(xiàn)為該位移量下的層錯(cuò)能達(dá)到了最大值。當(dāng)位移量為時(shí)，層錯(cuò)能達(dá)到了局部極小值。此外，C 在n ＝1，2，3 處的GSFE 曲線變化趨勢(shì)與γ-Fe 的一致，分別在位移量為和時(shí)達(dá)到局部最大值與局部最小值，即γUSF和γISF。當(dāng)C 遠(yuǎn)離層錯(cuò)面時(shí)，γUSF與γISF均逐步下降，都在n ＝3時(shí)降至最低。同時(shí)，n ＝3 位點(diǎn)處自由能最低，C 此時(shí)應(yīng)處于最穩(wěn)定狀態(tài)，故Fe24C1 模型的C取n ＝3 位點(diǎn)。文獻(xiàn)［24］提到，層錯(cuò)運(yùn)動(dòng)會(huì)將C擠出層錯(cuò)區(qū)域，而在本文計(jì)算模型中，n ＝3 處的C 處于層錯(cuò)區(qū)域外，因此C位于n ＝3處時(shí)的γISF應(yīng)為C對(duì)γ-Fe的γISF真實(shí)影響。與γ-Fe 相比，C 使γISF提高約20 mJ／m2，γUSF提高約38 mJ／m2。

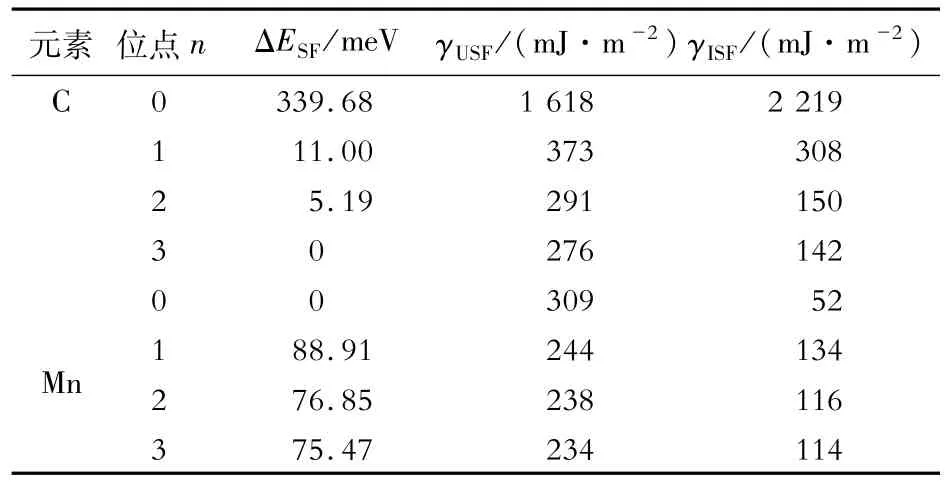
表2 Fe24C1 模型中C、Mn在不同位點(diǎn)對(duì)應(yīng)的γUSF與γISFTable 2 γUSF and γISF corresponding C and Mn at different sites in Fe24C1 model

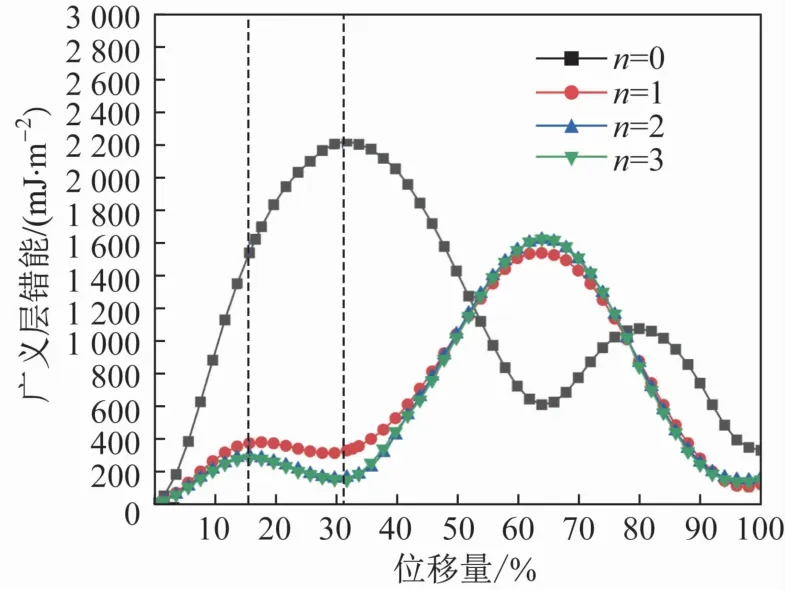
圖4 C處于不同位點(diǎn)時(shí)的廣義層錯(cuò)能曲線Fig.4 Generalized stacking fault energy curves of C at different sites

表2 還列出了Mn與層錯(cuò)面之間的距離不同時(shí)的γUSF和γISF。Mn位于n ＝0 位點(diǎn)時(shí)γISF最低，為52 mJ／m2，相比于γ-Fe，γISF約降低70 mJ／m2。當(dāng)Mn遠(yuǎn)離層錯(cuò)面時(shí)，對(duì)γISF的影響逐漸減弱直至趨近于γ-Fe。此外，當(dāng)Mn 遠(yuǎn)離層錯(cuò)面時(shí)，γUSF呈下降趨勢(shì)，說(shuō)明隨著Mn的遠(yuǎn)離，發(fā)生變形的勢(shì)壘降低。從自由能的角度考慮，Mn在n ＝0 位點(diǎn)處，ESF最低，故Mn在此位點(diǎn)時(shí)最穩(wěn)定。

確定C、Mn 在層錯(cuò)模型中最穩(wěn)定的位點(diǎn)后，按圖1 所示進(jìn)行“二次剪切”，計(jì)算γUTF與γTSF，結(jié)果如表3 所示。由表3 知，γ-Fe的γUTF為420 mJ／m2，加入C 后γUTF提高，為443 mJ／m2，說(shuō)明形成孿晶的勢(shì)壘上升；加入Mn 后γUTF大幅度下降，為174 mJ／m2，說(shuō)明形成孿晶的勢(shì)壘下降。

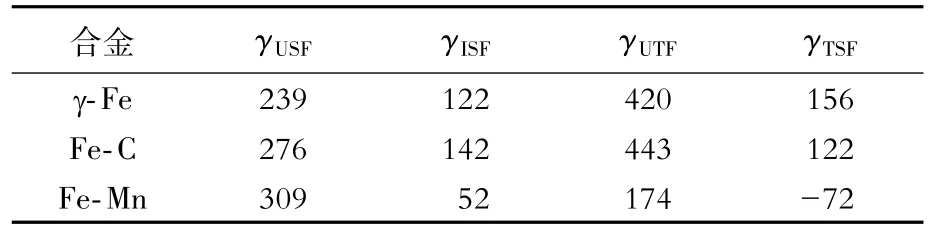
表3 C、Mn在γ-Fe中最穩(wěn)定位點(diǎn)對(duì)應(yīng)的γUSF、γISF、γUTF、γTSFTable 3 γUSF，γISF，γUTF，γTSF of C，Mn at the most stable sites in γ-FemJ／m2

2.3 變形機(jī)制預(yù)測(cè)

依據(jù)表3 的層錯(cuò)能計(jì)算孿晶判據(jù)，結(jié)果如表4 所示。γ-Fe的γISF遠(yuǎn)高于0，層錯(cuò)難以形成。按照γd理論，γ-Fe 的γd值介于0 ～2 之間，表明變形時(shí)兼具孿晶與滑移，而PTwinning的值為8.92，表明γ-Fe變形時(shí)具有較弱的孿晶形成能力。綜上，γ-Fe變形機(jī)制應(yīng)以滑移為主，兼具少量孿晶。

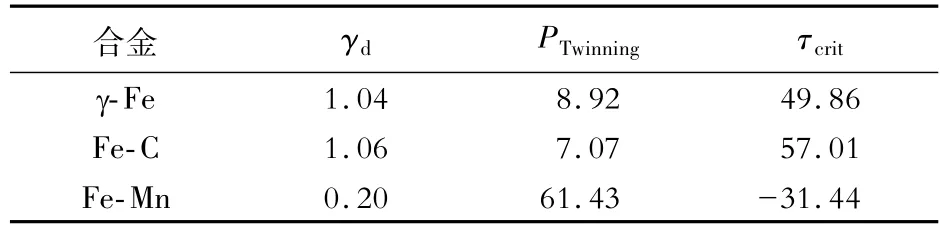
表4 孿晶判據(jù)計(jì)算結(jié)果Table 4 Calculated twinning criteria

加入C后，γISF上升，滑移更容易形成。另一方面，C導(dǎo)致γd上升，相比于γ-Fe，滑移的比例增加。同時(shí)，γUTF比γ-Fe 的高，使PTwinning下降、臨界孿晶應(yīng)力τcrit上升，因而加入C 后孿晶形成能力比γ-Fe更弱，F(xiàn)e-C的變形機(jī)制以滑移為主。

Fe23Mn1 模型中，Mn 的加入使γISF顯著下降，但仍遠(yuǎn)大于0，故層錯(cuò)難以形成。相較于γ-Fe，F(xiàn)e23Mn1 的γd大幅度下降，PTwinning大幅度上升，因此Mn在一定程度上有利于形成孿晶。同時(shí)，加Mn后臨界孿晶應(yīng)力τcrit大幅度降低，說(shuō)明Mn的存在可能比γ-Fe 更容易形成孿晶。綜上，F(xiàn)e-Mn變形時(shí)以滑移為主，孿晶為輔。

3 結(jié)論

（1）NM 態(tài)γ-Fe 的γISF為－400 mJ／m2，AFM態(tài)的γISF為122 mJ／m2，磁性對(duì)γISF的貢獻(xiàn)約為520 mJ／m2。反鐵磁γ-Fe變形時(shí)以滑移為主，孿晶形成能力較弱。

（2）C受層錯(cuò)運(yùn)動(dòng)的排斥作用，在層錯(cuò)區(qū)域外最穩(wěn)定。C 會(huì)提高γ-Fe 的γISF至144 mJ／m2。相比于γ-Fe，C 的存在使滑移更容易，孿晶更難形成。

（3）Mn 在層錯(cuò)面上最穩(wěn)定，使γISF降低至52 mJ／m2。加入Mn 后變形仍以滑移為主，但孿晶形成能力強(qiáng)于γ-Fe。