例析高考中直線與圓相切問題

袁海軍

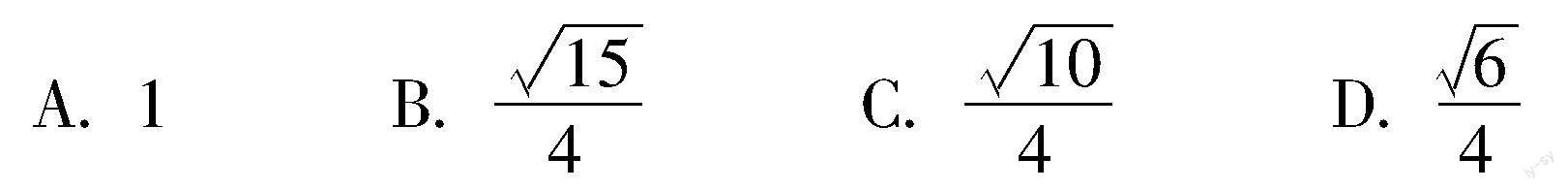
引例.（2023年新高考全國(guó)1卷第6題）

過點(diǎn)（0，-2）與圓x2+y2-4x-1=0相切的兩條直線的夾角為α，則sin α=（）

答案：B.

解析：本題考查了直線與圓的位置關(guān)系，重點(diǎn)考查相切問題，以下從三個(gè)角度來進(jìn)行求解：

點(diǎn)評(píng)：本題考查了直線與圓的位置關(guān)系，重點(diǎn)考查相切問題，可從切線方程、切線長(zhǎng)，切點(diǎn)三角形等方面入手，其難度不大.此題的解法相對(duì)容易，屬常規(guī)思路通法求解，思路一：根據(jù)切線的性質(zhì)求切線長(zhǎng)，轉(zhuǎn)化到切點(diǎn)三角形的一個(gè)內(nèi)角，并結(jié)合二倍角公式運(yùn)算求解；思路二：根據(jù)切線方程結(jié)合點(diǎn)到直線的距離公式可得k2+8k+1=0，利用韋達(dá)定理結(jié)合夾角公式運(yùn)算求解；思路三：根據(jù)切線的性質(zhì)求切線長(zhǎng)，轉(zhuǎn)化到有公共邊且對(duì)角互補(bǔ)的兩個(gè)三角形，再結(jié)合余弦定理運(yùn)算求解．

針對(duì)此題我們來進(jìn)一步探討有關(guān)直線與圓的相切問題：

1.定義：直線與圓只有一個(gè)公共點(diǎn).

2.方法：幾何法：圓心到直線的距離d等于半徑長(zhǎng)r，即（d=r）.

代數(shù)法：聯(lián)立直線與圓的方程，消元后得到關(guān)于x（或y）的一元二次方程，方程有唯一的實(shí)數(shù)解，即（Δ=0）.

3.基本類型：

（1）求過圓上的一點(diǎn)（x0，y0）的切線方程：

（2）求過圓外一點(diǎn)（x0，y0）的圓的切線方程：

①幾何方法：當(dāng)斜率存在時(shí)，設(shè)為k，則切線方程為y-y0=k（x-x0），

即kx-y+y0-kx0=0.由圓心到直線的距離等于半徑長(zhǎng)，即可得出切線方程.

②代數(shù)方法：當(dāng)斜率存在時(shí)，設(shè)為k，則切線方程為y-y0=k（x-x0），即y=kx-kx0+y0，代入圓的方程，得到一個(gè)關(guān)于x的一元二次方程，由Δ=0，求得k，切線方程即可求出．

（3）在求過一定點(diǎn)的圓的切線方程時(shí)，應(yīng)首先判斷定點(diǎn)與圓的位置關(guān)系，若點(diǎn)在圓上，則該點(diǎn)為切點(diǎn)，切線只有一條；若點(diǎn)在圓外，切線有兩條；若點(diǎn)在圓內(nèi)，則切線不存在．

4.常用結(jié)論：

①過圓x2+y2=r2上點(diǎn)P（x0，y0）的圓的切線方程為x0x+y0y=r2.

②過圓（x-a）2+（y-b）2=r2上點(diǎn)P（x0，y0）的圓的切線，

方程為（x-a）（x0-a）+（y-b）（y0-b）=r2.

③過圓x2+y2=r2外一點(diǎn)P（x0，y0）作圓的兩條切線，則兩切點(diǎn)所在直線（切點(diǎn)弦），

方程為x0x+y0y=r2.

④過圓（x-a）2+（y-b）2=r2外一點(diǎn)P（x0，y0）作圓的兩條切線，則兩切點(diǎn)所在直線（切點(diǎn)弦）方程為（x-a）（x0-a）+（y-b）（y0-b）=r2.

下面我們?cè)賮砜唇鼛啄甑乃牡栏呖荚}，并從多維度，多方法進(jìn)行分析與求解．

例1.（2023年高考全國(guó)乙卷文數(shù)第11題）

已知實(shí)數(shù)x，y滿足x2+y2-4x-2y-4=0，則x-y的最大值是（）

答案：C.

解法1：判別式法

解法2：幾何法

解法3：三角換元法

點(diǎn)評(píng)：本題作為選擇題的第11題，言簡(jiǎn)意賅，方法明確，難度中檔.看似是一個(gè)求函數(shù)最大值問題，其本質(zhì)是考查直線與圓的相切問題，要求考生學(xué)會(huì)將函數(shù)問題轉(zhuǎn)化為解幾問題，并結(jié)合直線與圓的相關(guān)知識(shí)，利用幾何法，代數(shù)法進(jìn)行求解.思路一：令x-y=k進(jìn)行代入消元，利用判別式法即可；思路二：通過整理得（x-2）2+（y-1）2=9，利用三角換元法即可，思路三：整理出圓的方程，設(shè)x-y=k，利用圓心到直線的距離小于等于半徑即可．

例2.（2021年新高考全國(guó)Ⅰ卷第11題）

已知點(diǎn)P在圓（x-5）2+（y-5）2=16上，點(diǎn)A（4，0），B（0，2），則（）

A.點(diǎn)P到直線AB的距離小于10

B.點(diǎn)P到直線AB的距離大于2

答案：ACD.

點(diǎn)評(píng)：本題作為多項(xiàng)選擇題，要求考生考慮全面，逐項(xiàng)論證.此題表面上考查動(dòng)點(diǎn)到定直線的距離和動(dòng)直線與定直線夾角的最值問題，其本質(zhì)還是考查直線與圓的相切問題，要求考生學(xué)會(huì)將最值問題用極端位置法處理，利用圖形簡(jiǎn)單明了.

例3.（2020年高考全國(guó)新課標(biāo)1卷理數(shù)第11題）

已知⊙M：x2+y2-2x-2y-2=0，直線l：2x+y+2=0，P為l上的動(dòng)點(diǎn)，過點(diǎn)P作⊙M的切線PA，PB，切點(diǎn)為A，B，當(dāng)|PM|·|AB|最小時(shí)，直線AB的方程為（）

A.2x-y-1=0B.2x+y-1=0

C.2x-y+1=0D.2x+y+1=0

答案：D

解法1：公共弦法

以MP為直徑的圓的方程為（x-1）（x+1）+y（y-1）=0，即 x2+y2-y-1=0，兩圓的方程相減可得：2x+y+1=0，即為直線AB的方程. 故選：D．

解法2：切點(diǎn)弦法

由公式可得P（-1，0）的切點(diǎn)弦方程為（xP-1）（x-1）+（yP-1）（y-1）=4，即AB的方程為：2x+y+1=0. 故選：D．

點(diǎn)評(píng)：本題主要考查直線與圓的位置關(guān)系，最值問題，破解此題的關(guān)鍵是會(huì)轉(zhuǎn)化，即把|PM|·|AB|的最小值問題層層轉(zhuǎn)化，最終轉(zhuǎn)化為|PM|的最小值，從而轉(zhuǎn)化到點(diǎn)到直線的距離的最小值問題.考查的核心素養(yǎng)是邏輯推理，直觀想象，數(shù)學(xué)運(yùn)算.在思路二中直接采用切點(diǎn)弦公式求解，需巧記將圓方程的兩變量各“代一半”的模式.

例4.（2022年新高考全國(guó)1卷第15題）

寫出與圓x2+y2=1和（x-3）2+（y-4）2=16都相切的一條直線的方程 ．

解析：圓x2+y2=1的圓心坐標(biāo)為O（0，0），半徑r1=1，圓（x-3）2+（y-4）2=16的圓心坐標(biāo)為C（3，4），半徑r2=4，如圖：∵|OC|=r1+r2，∴兩圓外切，由圖可知，與兩圓都相切的直線有三條．

∴與圓x2+y2=1和（x-3）2+（y-4）2=16都相切的一條直線的方程為：

x=-1（填3x+4y-5=0，7x-24y-25=0都正確）．

故答案為：x=-1（填3x+4y-5=0，7x-24y-25=0都正確）．

點(diǎn)評(píng)：本題考查兩圓的公切線問題，要先判斷兩圓的位置關(guān)系，再結(jié)合直線與圓相切的幾何意義，分情況討論即可.此題因?yàn)閮蓤A是外切，它有三條公切線，通過作圖觀察其中的一條比較容易求出.這也是開放型試題的一個(gè)優(yōu)點(diǎn)，要求考生快速求出一個(gè)答案即可，不要求全面求解．

鞏固練習(xí)題

（1）求過點(diǎn)P的圓C的切線方程；

（2）求過點(diǎn)M的圓C的切線方程，并求出切線長(zhǎng)．

2.設(shè)m，n∈R，若直線（m+1）x+（n+1）y-2=0與（x-1）2+（y-1）2=1 相切，則m+n的取值范圍是．

3.在平面直角坐標(biāo)系xOy中，已知圓C：x2+（y-3）2=2，點(diǎn)A是x軸上的一個(gè)動(dòng)點(diǎn)，AP，AQ分別切圓C于P，Q兩點(diǎn)，則線段PQ的取值范圍是．

參考答案：

參考答案：

1.解析：由題意得圓心C（1，2），半徑長(zhǎng)r=2．

（2）因?yàn)椋?-1）2+（1-2）2=5>4，所以點(diǎn)M在圓C外部．

當(dāng)過點(diǎn)M的直線斜率不存在時(shí)，直線方程為：x=3，又點(diǎn)C（1，2）到直線x=3的距離d=3-1=2=r，所以直線x=3是圓的一條切線．

當(dāng)切線的斜率存在時(shí)，設(shè)切線方程為y-1=k（x-3），即y=kx-3k+1，