氣-膜耦合作用對充氣薄膜管動力特性的影響

王曉峰，付慧杰，楊慶山

(1.北京交通大學土木建筑工程學院，北京 100044；2.重慶大學土木工程學院，重慶 400044)

充氣膜因質量輕、折疊體積小、成型快等優點，廣泛應用于土木工程的大跨建筑結構和航空航天領域的空間可展結構。充氣膜屬于柔性結構，通過內充氣壓使外圍薄膜產生預張力而獲得剛度，在荷載作用下易產生較大的變形，從而引起內充氣體體積和壓力的顯著改變。而內充氣壓的變化又影響外圍薄膜的張拉應力，進而影響充氣膜的剛度和變形。這種內充氣體壓力與外圍薄膜變形之間的耦合作用(氣-膜耦合作用)對充氣膜的力學行為產生重要影響。充氣薄膜管屬于氣肋式充氣膜，多用于薄膜結構的支撐構件，其動力特性必然對整個薄膜結構的動力行為產生重要影響。研究氣-膜耦合作用對充氣薄膜管動力特性的影響，有助于準確認識其動力性能，保證薄膜結構設計、計算的合理性和工程應用的可靠性。

現有文獻多關注充氣膜的靜力性能，在形態分析[1-5]、充氣階段的平衡構形[6-9]、外圍薄膜的力學性能[10-16]、接觸力學問題[17-21]以及褶皺變形的影響[22-29]等方面進行了研究。關于充氣膜動力性能的研究則相對較少，對于充氣薄膜管，僅涉及自振特性分析[30-33]和充氣展開過程中的動力性能分析[34-37]這兩個方面。

而目前充氣膜力學性能的研究，通常將內充氣壓等效為外圍薄膜的靜力邊界條件，或者假定內充氣體滿足理想氣態方程[38-39]，而考慮氣-膜耦合作用影響的研究文獻很少。文獻[40]通過將外圍流場離散為三維聲學流體單元對充氣薄膜梁進行濕模態分析，通過與相應的干模態分析結果進行對比，研究了外部流場對充氣薄膜梁動力特性的影響。文獻[41 - 42]假定內充氣體為非定常、可壓縮的理想氣體，研究了充氣薄膜管展開過程中氣-固耦合作用的影響。

本文基于作者對氣-膜耦合作用的靜力研究成果[43-44]，對充氣薄膜管的動力特性進行有限元分析，研究氣-膜耦合作用對自振特性的影響規律。考慮到充氣薄膜管外圍薄膜質量輕，內充氣體的附加質量在總質量中占有較大的比重，也對其影響作用進行探究。通過將內充氣體看作小擾動線性勢流以考慮氣-膜耦合作用和內充氣體附加質量的影響。借助商用有限元軟件ADINA，建立內充氣體的三種等效模型，分別將內充氣體作用等效為外圍薄膜靜力邊界條件(模型M1)，同時考慮內充氣體附加質量影響的靜力邊界條件(模型M2)以及小擾動線性勢流體(模型M3)，通過將其相應的有限元分析結果進行對比，研究氣-膜耦合作用和內充氣體附加質量對充氣薄膜管動力特性的影響及其隨初始內壓、長細比、膜厚和端部約束類型等因素的變化規律。

1 理論基礎

外圍薄膜和內充氣體的物理特性及其相互耦合作用決定了充氣薄膜管的力學行為，因此，可通過外圍薄膜和內充氣體的力學微分方程以及氣-膜耦合作用方程建立充氣薄膜管的控制方程。

1.1 薄膜微分方程

假定薄膜的變形具有大轉動、小應變特點，而且在整個變形中保持為線彈性本構關系，即應力-應變關系滿足廣義胡克定律。同時，假定薄膜具有微小的抗彎剛度，其褶皺變形實際上是薄殼在壓應力作用下的局部屈曲，可基于式(1)給出的板殼穩定方程[45]通過非線性屈曲分析求得。

式中： Σ=σh，σ 為二維Cauchy 應力張量，h為薄膜厚度；為薄膜單位面積質量；x為二維位置矢量；x¨=?2x/?t2；x˙=?x/?t，t為時間；μ為單位面積阻尼系數；w為薄膜中面的撓度；w¨=?2w/?t2；，E為彈性模量，ν為泊松比；L為微分算子，且L=??? ； ?=?/?x為梯度算子；q為垂直于膜面的外荷載。式(1)為基于F?ppl-von Kármán 理論的板殼穩定方程。對該方程的位移場進行有限元離散，由變分原理可得離散后的薄膜動力方程為：

式中：MS和CS分別為薄膜的質量矩陣和阻尼矩陣；u¨=?2u/?t2；u˙=?u/?t；u為薄膜單元的結點位移向量；fin(u)為薄膜單元的結點內力向量，是單元結點位移的函數；fex=Q+PS，Q和PS分別為外荷載和內充氣壓所對應的薄膜單元結點外力向量。

1.2 內充氣體微分方程

充氣薄膜管中的內充氣體屬于封閉流場，因外圍薄膜變形而產生的擾動速度很小，可假定其為均勻、無旋、無粘的理想流體，且在變化過程中始終滿足等熵條件。這樣，內充氣體可看作線性有勢流體[46]，在小擾動條件下滿足波動方程[47]：

式中： ?2=?·?為拉普拉斯算子；c為音速；φ¨=?2φ/?t2； φ為速度勢函數，即

式中，vF為內充氣體速度矢量。式(3)為關于函數φ的線性微分方程，在其求解域內分片離散場函數φ，并通過Galerkin 法使加權余量為零，可得有限元離散格式的線性方程為[46]：

1.3 氣-膜耦合作用方程

當不考慮內充氣體的粘性時，充氣薄膜管在內充氣體和外圍薄膜耦合界面處，有：

式中：vF,n和pF分別為內充氣體在氣-膜耦合界面處的法向速度以及承受的薄膜壓力作用；vS,n和pS分別為外圍薄膜在氣-膜耦合界面處的法向速度以及承受的內充氣體壓力作用。由式(6)可以得到有限元離散后的耦合方程為[46]：

式中：T為薄膜位移投影到耦合界面法線方向的轉換矩陣；；NS為薄膜單元的形函數矩陣。將式(7)的第一式和第二式分別代入式(5)和式(2)得：

式(8)和式(9)為考慮氣-薄膜耦合作用的充氣薄膜管有限元離散方程。當充氣薄膜管的外荷載為零，且不考慮結構阻尼時，式(8)退化為：

式(9)和式(10)為考慮氣-膜耦合作用的充氣薄膜管自由振動方程。

2 有限元模型

根據式(9)和式(10)建立的考慮氣-膜耦合作用的充氣薄膜管自由振動方程，借助商用有限元軟件ADINA 對充氣薄膜管的動力特性進行有限元分析。根據1.1 節的基本假定，將外圍薄膜看作Kirchhoff 材料，采用四結點殼單元進行有限元離散；根據1.2 節的基本假定，對內充氣體采用八結點的線性勢流單元進行離散，以考慮內充氣體與外圍薄膜的耦合作用。充氣薄膜管兩端采用與試驗相同的金屬蓋板封閉，以便于與試驗結果進行比較。兩端金屬蓋板采用四結點殼單元進行離散。

圖1 給出了充氣薄膜管在膜厚h=0.075 mm、半徑r=50 mm、長細比λ=7、兩端固定、內壓P0=4 kPa情況下(其他材料參數如表1 所示)，前5 階自振頻率隨單元數量的變化情況。橫坐標num 為薄膜單元數量，縱坐標Δf為不同單元數量得到的同階頻率差值，n為頻率的階次。從圖1 可以看出，隨著薄膜單元數量的增加，頻率的差值逐漸減小，最終趨于零。

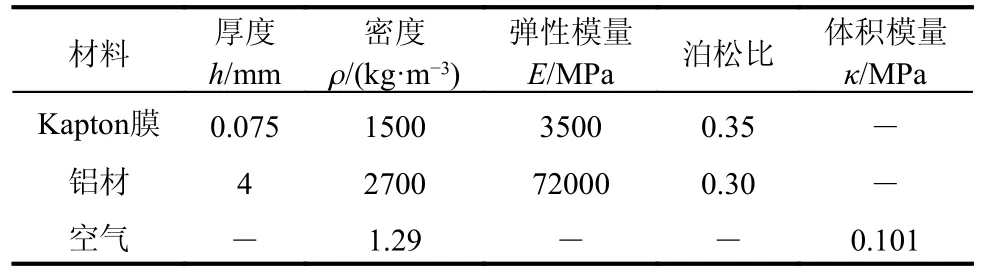
表1 充氣薄膜管材料參數[44]Table 1 Material properties of the inflated membrane tube[44]

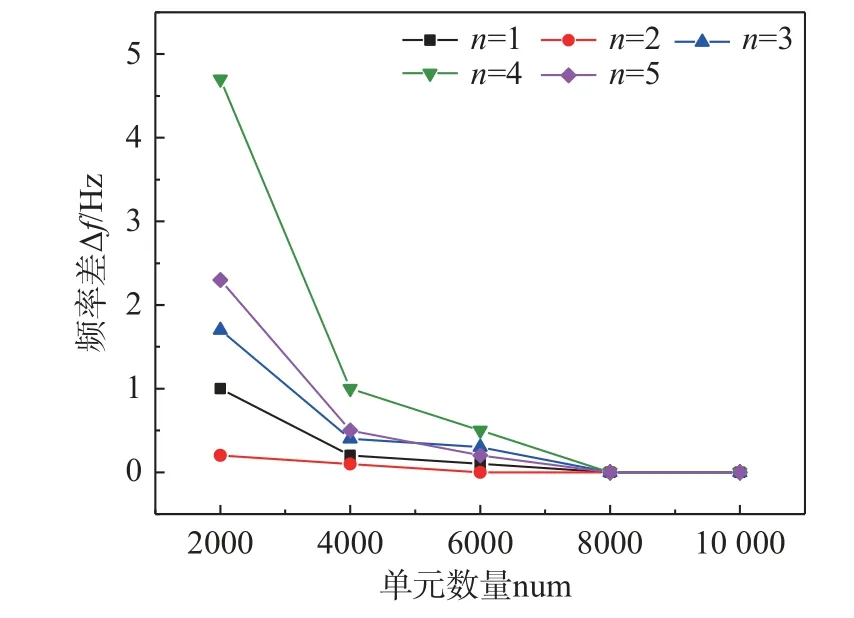
圖1 前5 階自振頻率隨單元數量變化情況[44]Fig.1 Variations of the first five-order natural frequencies with the element number[44]

根據圖1 給出的充氣薄膜管的前5 階自振頻率隨單元數量的變化情況，權衡其計算精度和計算時間，最終確定外圍薄膜的單元數量為8000 個，單元尺寸為3.93 mm×7.00 mm；內部勢流的單元數量為84 400 個，單元尺寸為(2.91 mm～3.93 mm)×(2.91 mm～3.93 mm)×7.00 mm；兩端蓋板的單元數量為844 個，單元尺寸為(2.91 mm～3.93 mm)×(2.91 mm～3.93 mm)。建立的有限元模型如圖2 所示。

圖2 充氣薄膜管有限元模型[44]Fig.2 Finite element model of the inflated membrane tube[44]

充氣薄膜管外部薄膜采用Kapton 膜材，內充氣體為空氣，兩端采用鋁制蓋板封閉，相應的材料參數如表1 所示。充氣薄膜管的端部蓋板剛度遠大于外圍薄膜，可將其看作剛性平面，通過約束其作為剛體的三個平動和三個轉動自由度來實現固定約束條件；通過約束其作為剛體的三個平動自由度和繞z軸(縱軸)和y軸(彎曲平面內的橫截面形心慣性軸)的轉動自由度來實現簡支約束條件。

具體有限元分析過程如下：

1) 通過對外圍薄膜、端蓋板采用四結點殼單元進行有限元離散，建立式(10)相應的結構離散模型。

2) 對內充氣體采用八結點的線性勢流單元進行有限元離散，建立式(9)相應的勢流場離散模型。

3) 通過薄膜單元和勢流單元在交界面上共享結點實現氣-膜耦合，形成式(9)和式(10)中的耦合矩陣A。

4) 在充氣薄膜管兩端施加邊界條件，然后對離散后的內充氣體施加質量流荷載使其達到初始內壓，同時使外圍薄膜產生預張應力。

5) 對充氣薄膜管進行模態分析，即通過Lanczos方法求解式(9)和式(10)確定的特征值問題，獲得其自振頻率和自振模態。

3 有限元模型驗證

3.1 靜力驗證

通過研發試驗裝置，對充氣薄膜管進行靜力加載試驗，驗證本文建立的考慮氣-膜耦合作用有限元模型在靜力分析時的正確性和精確性。靜力分析時的邊界條件如圖3 所示，研發的試驗裝置如圖4 所示。試驗中，通過砝碼施加豎向和橫向荷載；位移和內壓分別采用松下HG-C1100 激光位移計和數字差壓計進行量測；充氣設備為220 V單缸充氣泵，并在排氣口位置處安裝活塞用于氣壓微調，確保初始氣壓的精度。

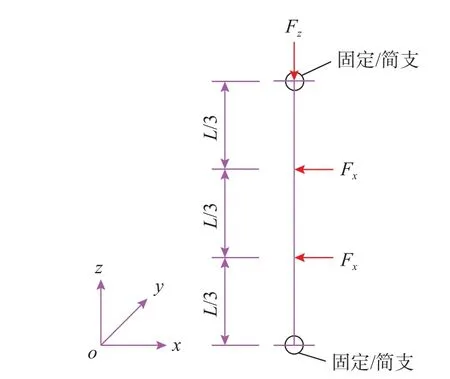
圖3 充氣薄膜管荷載作用示意圖[44]Fig.3 Diagram of the inflated membrane tube under load[44]

圖4 試驗裝置實物圖[44]Fig.4 Experimental setup[44]

圖5 給出了充氣薄膜管在直徑100 mm、長細比為7、膜厚75 μm 以及內充氣壓為6 kPa 情況下試驗與數值的對比結果。有限元模型信息和物理參數如第2 節所示，考慮了氣-膜耦合作用和內充氣體附加質量的影響。靜力有限元分析中，根據第1 階特征值屈曲模態施加初始缺陷，考慮幾何非線性的影響[44]。內充氣體為恒質量情況下內壓P、跨中橫向位移uH隨橫向荷載FH的變化曲線如圖5(a)、圖5(b)所示。

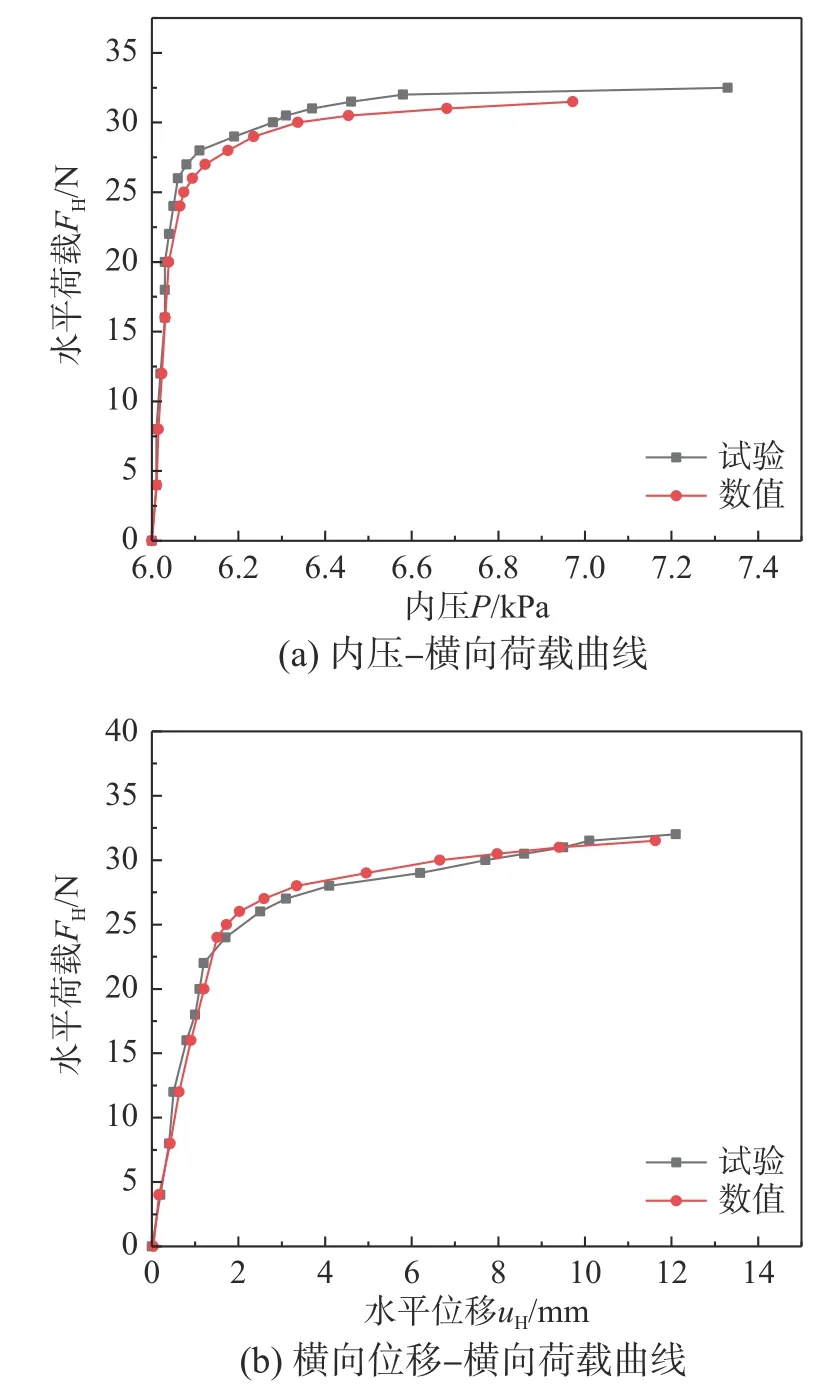
圖5 試驗和有限元分析結果對比Fig.5 Comparison between experimental and numerical results

從圖5 的對比結果可以看出，分別由試驗和有限元分析得到的內壓-荷載曲線以及位移-荷載曲線均吻合很好，從而驗證了本文建立的充氣薄膜管有限元模型在考慮氣-膜耦合作用和內充氣體附加質量影響的情況下，靜力分析的正確性和精確性。

3.2 動力特性驗證

通過與文獻[48]中相應的試驗和數值計算結果進行對比，驗證本文建立的考慮氣-膜耦合作用的充氣薄膜管有限元模型在模態分析中的有效性和精確性。文獻[48]中充氣薄膜管兩端為固定約束，具體幾何及物理參數取值如表2 所示。

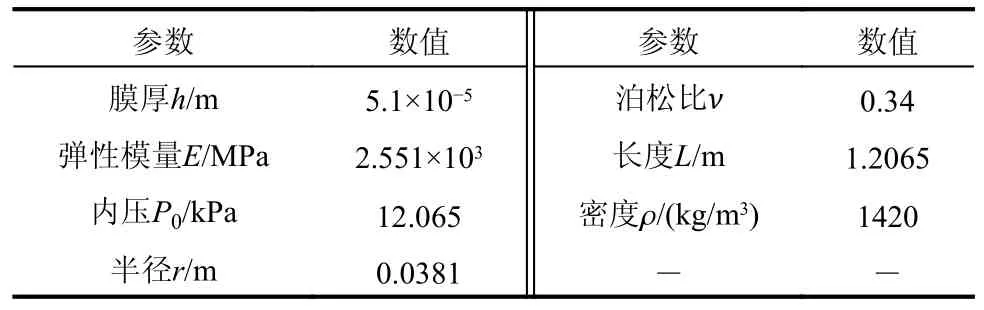
表2 充氣薄膜管參數[48]Table 2 Parameters of the inflated membrane tube[48]

表3 給出了分別由文獻[48]試驗和本文有限元分析得到的前3 階自振模態形狀。表4 給出了分別由文獻[48]試驗和有限元分析(將內充氣體等效為外圍薄膜的靜力邊界條件而未考慮氣-膜耦合作用)得到的前3 階自振頻率以及相應的本文有限元分析(考慮氣-膜耦合作用)結果。

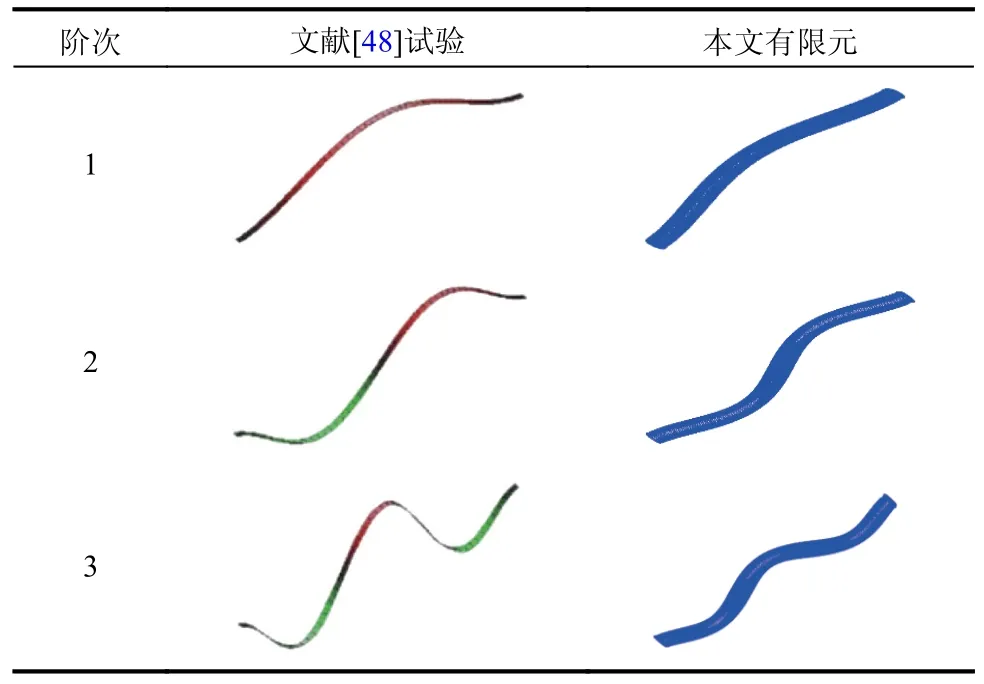
表3 充氣薄膜管自振模態Table 3 Modal shapes of the inflated membrane tube

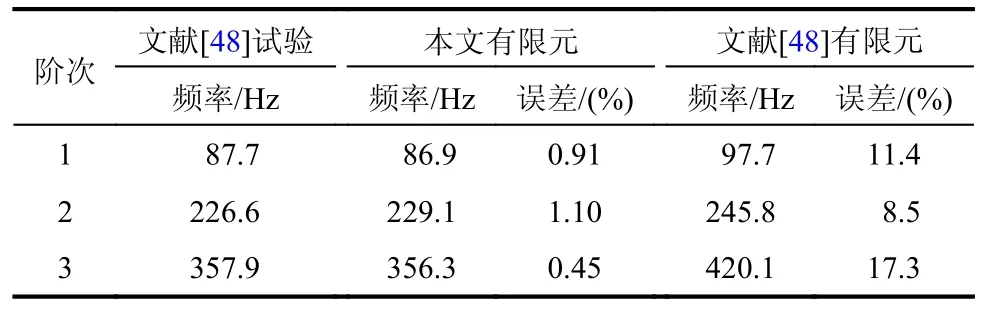
表4 充氣薄膜管自振頻率Table 4 Natural frequencies of the inflated membrane tube

由表3 和表4 可知，由本文有限元模型得到的前3 階自振模態和相應頻率與文獻[48]試驗結果吻合很好，頻率最大誤差為1.1%。而文獻[48]在有限元分析中，由于沒有考慮氣-膜耦合作用以及內充氣體附加質量的影響，其頻率計算結果與試驗結果差異較大。可見，將內充氣體作用等效為外圍薄膜的靜力邊界條件會導致較大的計算誤差，應考慮氣-膜耦合作用的影響。而本文建立的考慮氣-膜耦合作用的充氣薄膜管有限元模型具有良好的精度，可用于研究氣-膜耦合作用對充氣薄膜管動力特性的影響及其隨參數的變化規律。

4 氣-膜耦合作用對動力特性的影響

基于如表5 所示的三種內充氣體等效模型(M1、M2、M3)，對充氣薄膜管進行模態分析。通過將三種模型的計算結果進行對比，研究氣-膜耦合作用對充氣薄膜管動力特性的影響及其隨初始內壓、長細比、膜厚以及端部約束類型的變化規律，并探究內充氣體附加質量的影響程度。各影響因素的取值范圍以及相應的其他參數取值情況如表6所示。由于三種模型對模態形狀沒有明顯影響，4.1 節～4.4 節只給出由模型M3(將內充氣體等效為有勢流體)得到的前5 階模態形狀。

表5 內充氣體的等效模型Table 5 Equivalent models of the inner air

表6 影響因素及其他參數取值Table 6 Values of the influencing factors and other parameters

4.1 隨初始內壓的變化

對初始內壓分別為2 kPa、4 kPa、6 kPa、8 kPa、10 kPa、12 kPa 情況下的充氣薄膜管進行自振特性分析，研究氣-膜耦合作用隨初始內壓的變化規律，其他參數及物理特性取值分別如表6 和表1 所示。表7 給出了模型M3 的前5 階自振模態形狀。

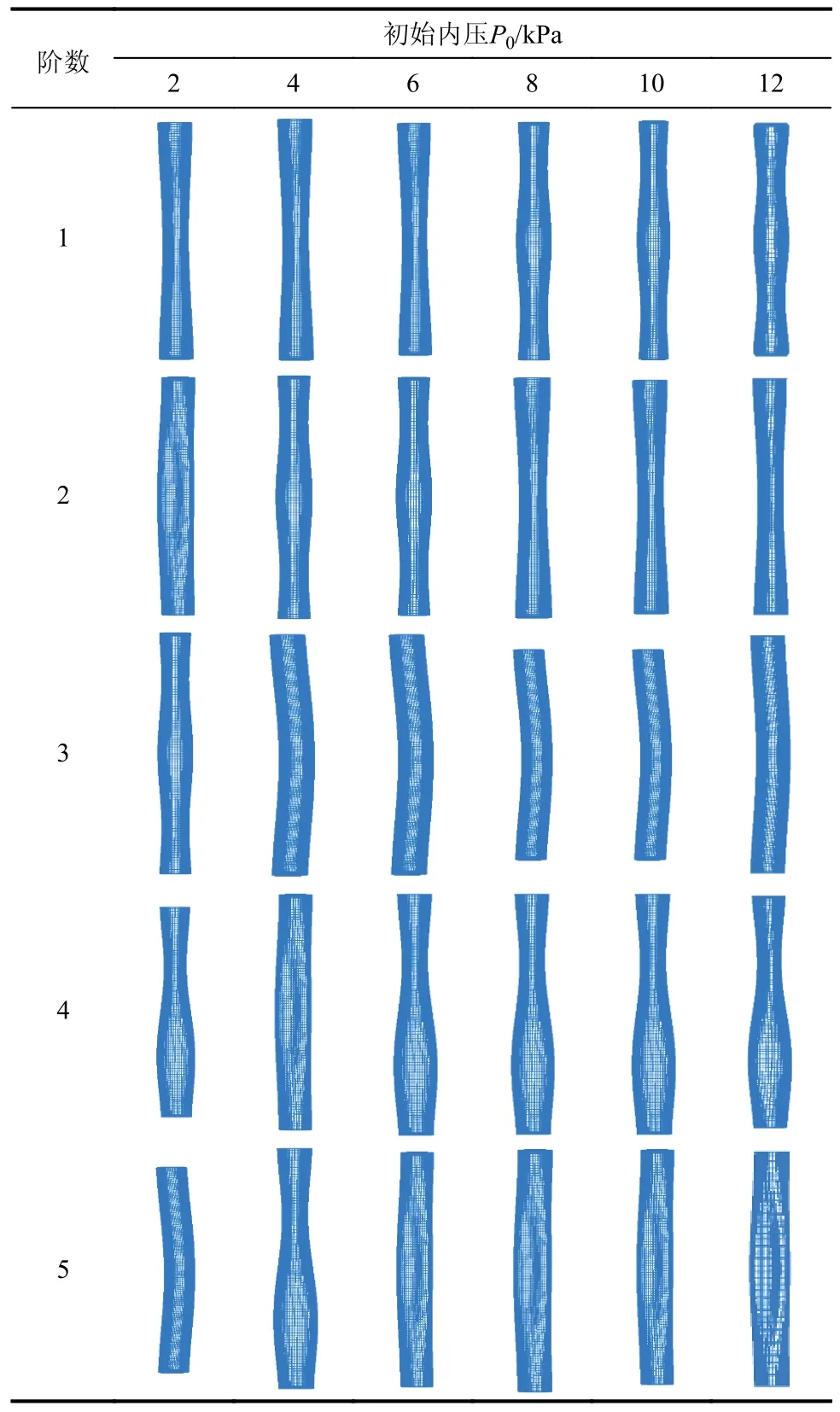
表7 不同初始內壓情況下的前5 階自振模態Table 7 The first five mode shapes for different initial internal pressures

從表7 可以看出，初始內壓對充氣薄膜管自振模態形狀出現階次的影響較為顯著。隨著內壓的升高，中間凹陷的自振模態從P0≤6 kPa 的第1 階推后到P0>6 kPa 的第2 階；單側鼓凸的自振模態從P0=2 kPa 的第2 階推后到P0=4 kPa 的第4 階以及P0≥6 kPa 的第5 階；中間鼓凸的自振模態從P0=2 kPa 的第3 階提前到4 kPa≤P0≤6 kPa 的第2 階以及P0≥8 kPa 的第1 階；上部凹陷下部鼓凸的自振模態從P0=2 kPa 第4 階推后到P0=4 kPa的第5 階，然后又提前到P0≥6 kPa 的第4 階；整體的彎曲模態從初始內壓P0=2 kPa 的第5 階，提前到P0≥4 kPa 的第3 階。從表7 還可以看出，當P0≥8 kPa 后，相同自振模態形狀的階次不再發生變化。

但三種模型(即M1、M2 和M3)得到的同一階次自振模態形狀基本相同，所以氣-膜耦合作用以及內充氣體的附加質量對充氣薄膜管的自振模態形狀沒有明顯影響。隨著內充氣壓的升高，外圍薄膜管的應力分布發生改變，進而引起充氣薄膜管不同位置相對剛度的變化，所以對相同模態形狀出現的階次產生影響作用。

圖6 給出了模型M1 和模型M2 的前5 階頻率分別與模型M3 相應頻率的比值隨初始內壓的變化情況。fM1、fM2和fM3分別為由模型M1、模型M2和模型M3 得到的頻率，n為頻率的階次。

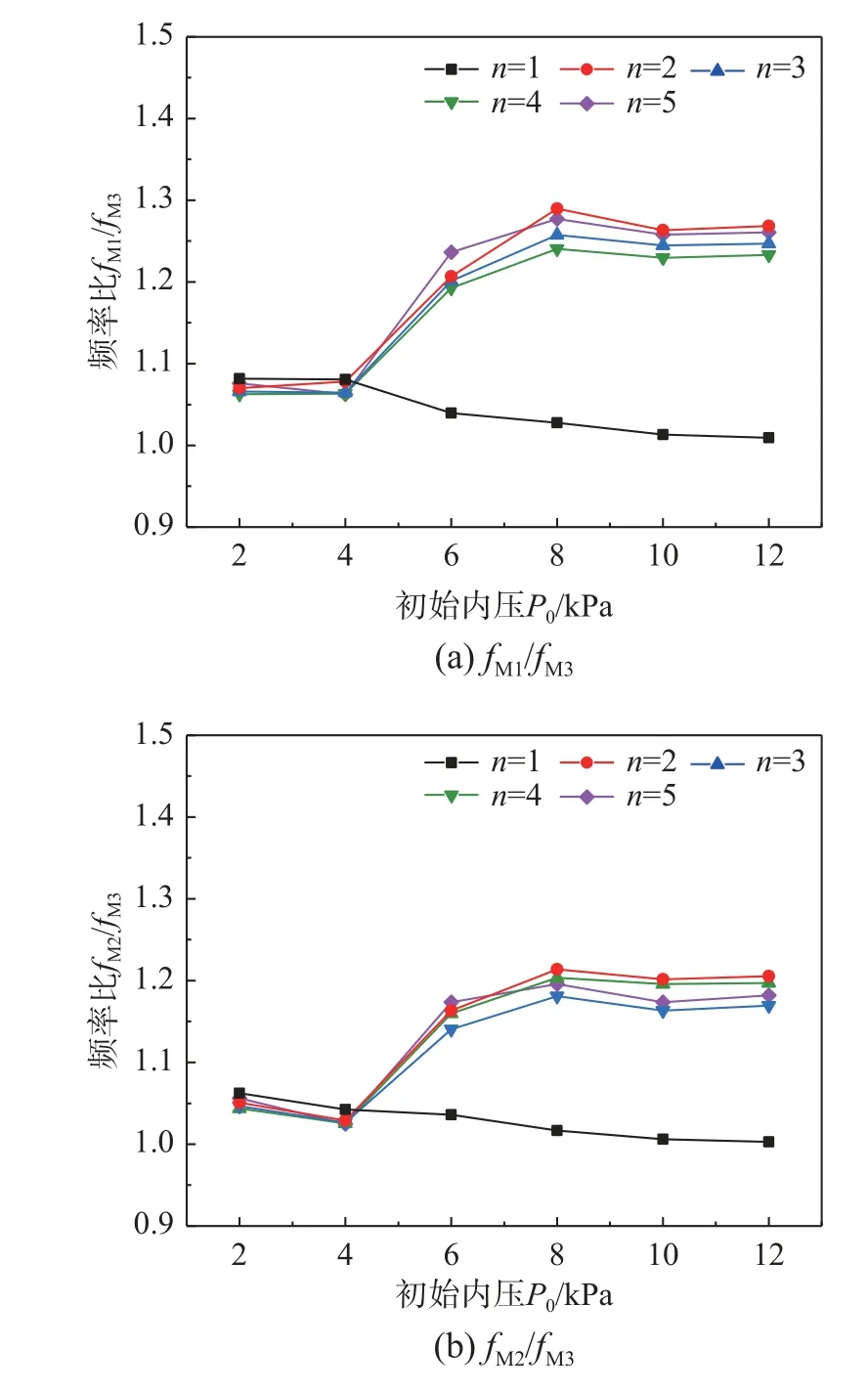
圖6 不同內壓下頻率比值曲線Fig.6 Ratios of frequencies for different internal pressures

從圖6(a)可以看出，初始內壓P0≤4 kPa 時，各階頻率比值fM1/fM3未見明顯變化，而當P0≥4 kPa后，第1 階頻率比值與第2 階～第5 階頻率的比值隨初始內壓增加呈現不同的變化規律：第1 階頻率的比值fM1/fM3隨初始內壓的升高而逐漸降低；第2 階～第5 階頻率的比值fM1/fM3均隨初始內壓的升高而較快增加，但在P0≥ 8 kPa 后又略有降低。

從圖6(b)可以看出，初始內壓P0≤4 kPa 時，各階頻率比值fM2/fM3均隨初始內壓升高而略有減小；但當P0≥4 kPa 后，第1 階頻率比值與第2 階～第5 階頻率的比值隨初始內壓增加呈現不同的變化規律，與圖6(a)所示相應曲線相似：第1 階頻率的比值fM2/fM3隨初始內壓的升高而逐漸降低，第2 階～第5 階頻率的比值fM2/fM3均隨初始內壓的升高先較快增加然后又略有減小，并逐漸趨于穩定。

由于模型M2 考慮了內充氣體附加質量的影響，相同初始內壓情況下的頻率要略低于模型M1的相應頻率，但兩者隨初始內壓的變化規律大致相同。模型M1 和模型M2 的自振頻率與模型M3 的自振頻率平均相差分別為14.73%和10.53%。可見，內充氣體附加質量的影響較小，平均為4.20%，而氣-膜耦合作用影響則較為顯著，平均為10.53%。

充氣薄膜管的剛度包括結構剛度Km和氣-膜耦合作用產生的剛度Kami兩部分。本文中，結構剛度Km是指由于外圍薄膜慣性矩、約束條件等因素產生的剛度總和；氣-膜耦合作用產生的剛度Kami是指由于內充氣體內壓和外圍薄膜變形之間的耦合作用而產生的剛度。薄膜管剛度Km影響占主導位置而氣-膜耦合作用影響較弱，則比值fM1/fM3和fM2/fM3較小，接近于1；薄膜管剛度Kami影響占主導位置，則氣-膜耦合作用影響較強，比值fM1/fM3和fM2/fM3遠大于1。薄膜管剛度Km和Kami兩者在對頻率影響作用中所占比重及其變化情況影響fM1/fM3和fM2/fM3的比值曲線形狀。隨初始內壓的升高，剛度Km和Kami均增大，但剛度Km在第1 階頻率中的影響作用中所占比重明顯增大，而剛度Kami在第2 階～第5 階頻率的影響作用中所占比重增大更為顯著。因此，fM1/fM3和fM2/fM3的頻率比值曲線呈現如圖6 所示的變化特征。但當初始內壓P0≥8 kPa 后，剛度Kami的影響作用中所占比重基本趨于穩定。

4.2 隨長細比的變化

對長細比λ 分別為6、8、10、12、14 情況下的充氣薄膜管進行自振特性分析，研究氣-膜耦合作用隨長細比的變化規律。其他參數同4.1 節。表8所示給出了模型M3 的前5 階自振模態形狀。

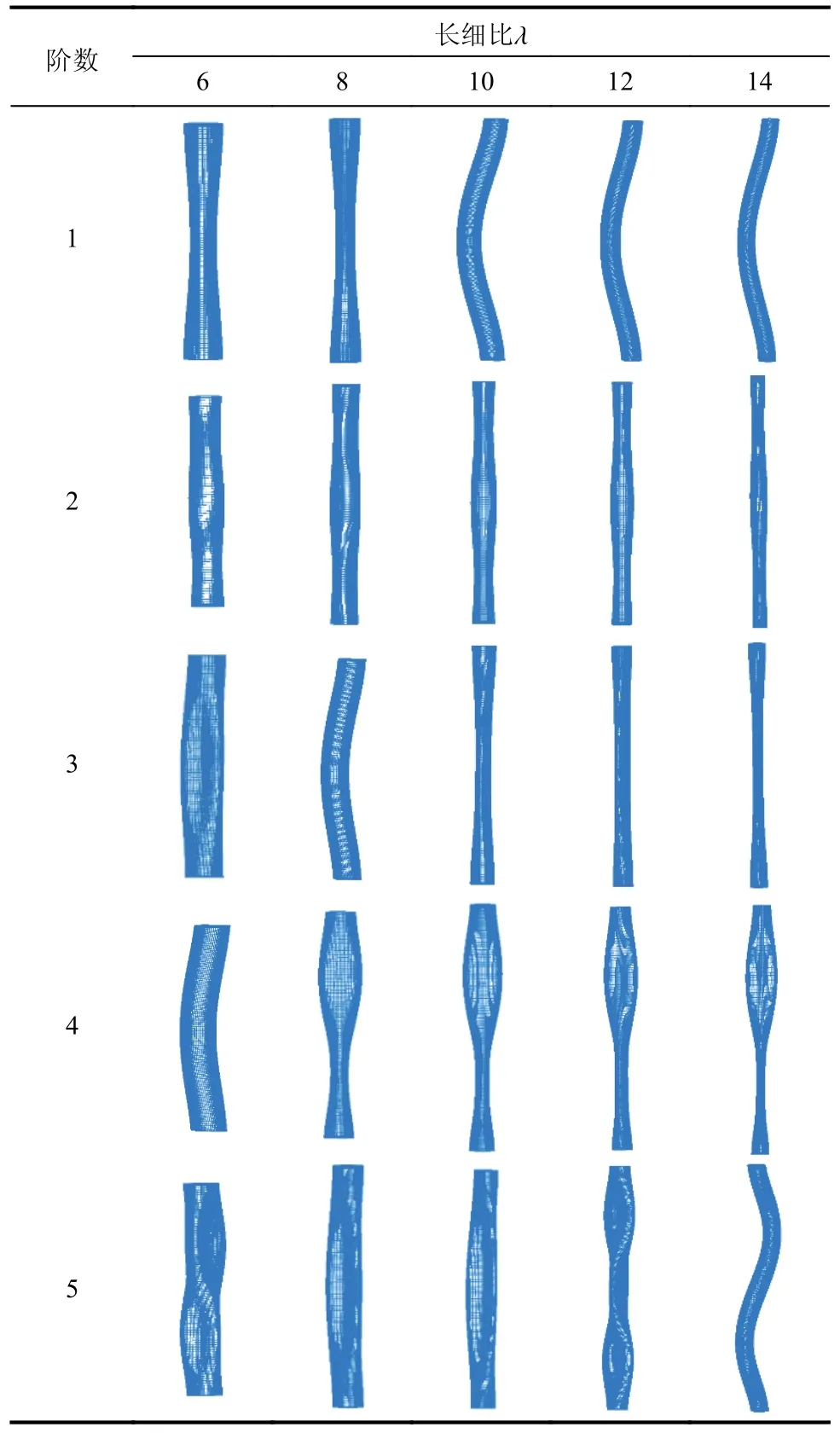
表8 不同長細比情況下前5 階自振模態Table 8 The first five mode shapes for different slenderness ratios

從表8 可以看出，長細比對充氣薄膜管自振模態出現階次的影響較為顯著。隨著長細比的增加，中間凹陷的自振模態從λ≤8 的第1 階推后到λ≥10 的第3 階；中間鼓凸的自振模態則始終為第2 階，并沒有隨長細比的增加發生變化；單側鼓凸的自振模態從λ=6 的第3 階推后到8≤λ≤10的第5 階以及λ>10 的更高階(表8 只給出前5 階)；整體的彎曲模態從長細比λ=6 的第4 階，提前到λ=8 的第3 階以及λ≥10 的第1 階；長細比λ≥8后，第4 階出現了充氣薄膜管上部鼓凸而下部凹陷的新自振模態，并且隨長細比的增加其階次沒有發生變化。此外，當長細比λ=14 時，第5 階出現“S”形彎曲自振模態，可以預測當長細比進一步增大，“S”形彎曲自振模態的階次可能會進一步提前。因為充氣薄膜管的整體彎曲模態階次隨著長細比的增加而降低，而其局部振動模態的階次則隨長細比的增加而升高。

圖7 給出了模型M1 和模型M2 的前5 階頻率分別與模型M3 相應階次頻率的比值隨長細比的變化情況。從圖7(a)和圖7(b)可以看出，模型M2由于考慮了內充氣體附加質量的影響，相同長細比情況下要低于模型M1 的相應頻率，與模型M3的頻率差異略小于模型M1 和模型M3 的頻率差異。頻率比值fM2/fM3與fM1/fM3平均相差約為4.06%。可見內充氣體附加質量對充氣薄膜管的自振頻率的影響較小。但氣-膜耦合作用對自振頻率則有顯著影響作用，模型M1 和模型M2 的自振頻率與模型M3 的自振頻率平均相差分別為22.41%和18.35%。

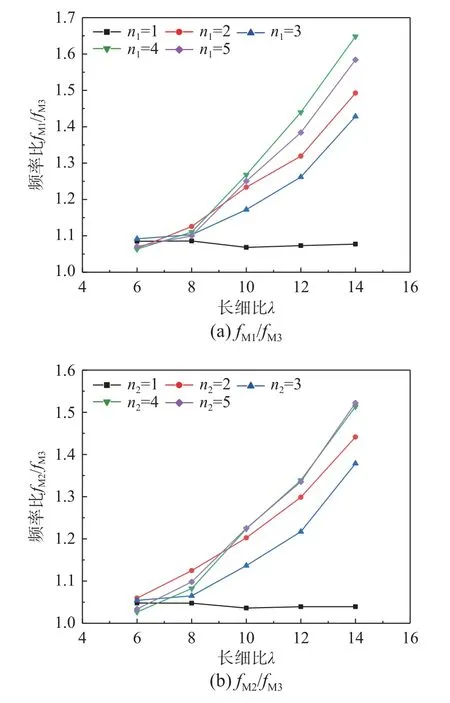
圖7 不同長細比情況下的頻率比值Fig.7 Ratios of frequencies for different slenderness ratios

從圖7(a)和圖7(b)中不同階頻率比值的變化曲線可以看出，氣-膜耦合作用的影響(fM1/fM3、fM2/fM3比值曲線)隨長細比的變化表現出因頻率階次不同而不同的規律：對第1 階自振頻率影響隨長細比沒有明顯變化，但對第2 階～第5 階自振頻率的影響則隨長細比的增加迅速增大。

隨長細比的增大，剛度Km和Kami均減小。但在第1 階頻率中的影響作用中，由于Kami的影響減小更快，Km的影響所占比重明顯增大；而在第2 階～第5 階頻率的影響作用中，由于Km的影響減小更快，Kami的影響所占比重增大更為顯著。因此，fM1/fM3和fM2/fM3的頻率比值曲線呈現如圖7 所示的變化特征。

圖8 給出了表8 所示第1 階彎曲模態對應的頻率比值fM1/fM3與fM2/fM3隨長細比的變化曲線。縱坐標中f表示頻率fM1或fM2。氣-膜耦合作用對第1 階彎曲模態的影響(fM1/fM3、fM2/fM3比值曲線)呈現出隨長細比的增加而非單調變化的特點。當長細比λ≤8 時，第1 階彎曲模態在充氣薄膜管的自振模態中為第4 階(λ=6)或第3 階(λ=8)。根據上一段的分析可知，對于第2 階～第5 階頻率，剛度Kami的影響更顯著，并隨長細比的增大其影響作用所占比重逐漸增大，因此，fM1/fM3和fM2/fM3比值曲線呈上升趨勢。當λ>8 后，第1 階彎曲模態躍遷為自振模態的第1 階。而對于第1 階頻率，剛度Km影響更顯著，并且隨長細比的變化，其影響作用所占比例始終占主導地位，所以fM1/fM3和fM2/fM3比值曲線會在λ=10 時突然減小，繼而隨長細比的變化，基本保持不變。

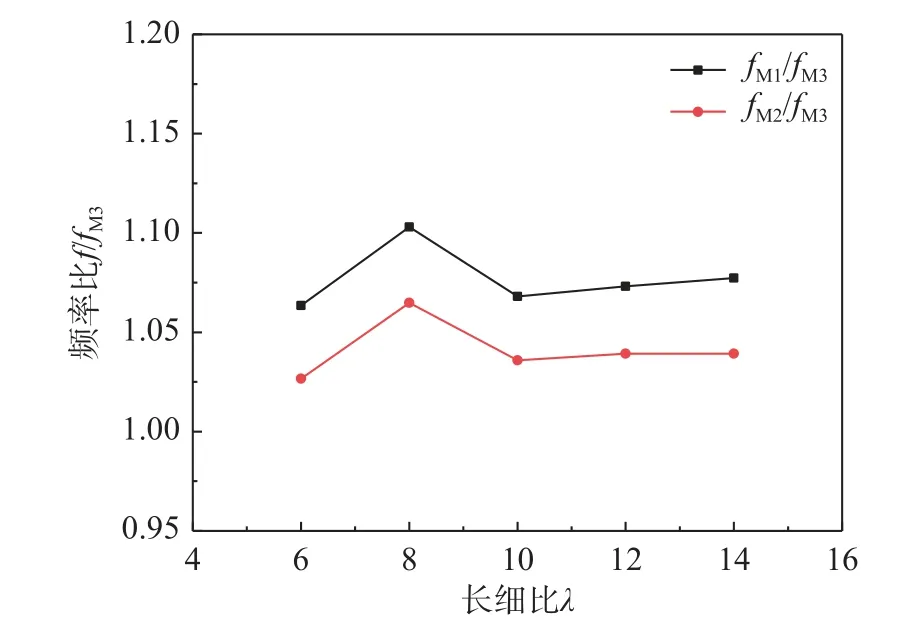
圖8 不同長細比情況下對應彎曲模態的頻率比值Fig.8 Ratios of frequencies corresponding to the bendingmode shape for different slenderness ratios

4.3 隨膜厚的變化

對膜厚分別為0.025 mm、0.050 mm、0.075 mm、0.100 mm 情況下的充氣薄膜管進行模態分析，研究氣-膜耦合作用隨膜厚的變化規律，其他參數同4.1 節。由模型M3 得到的前5 階自振模態如表9所示。

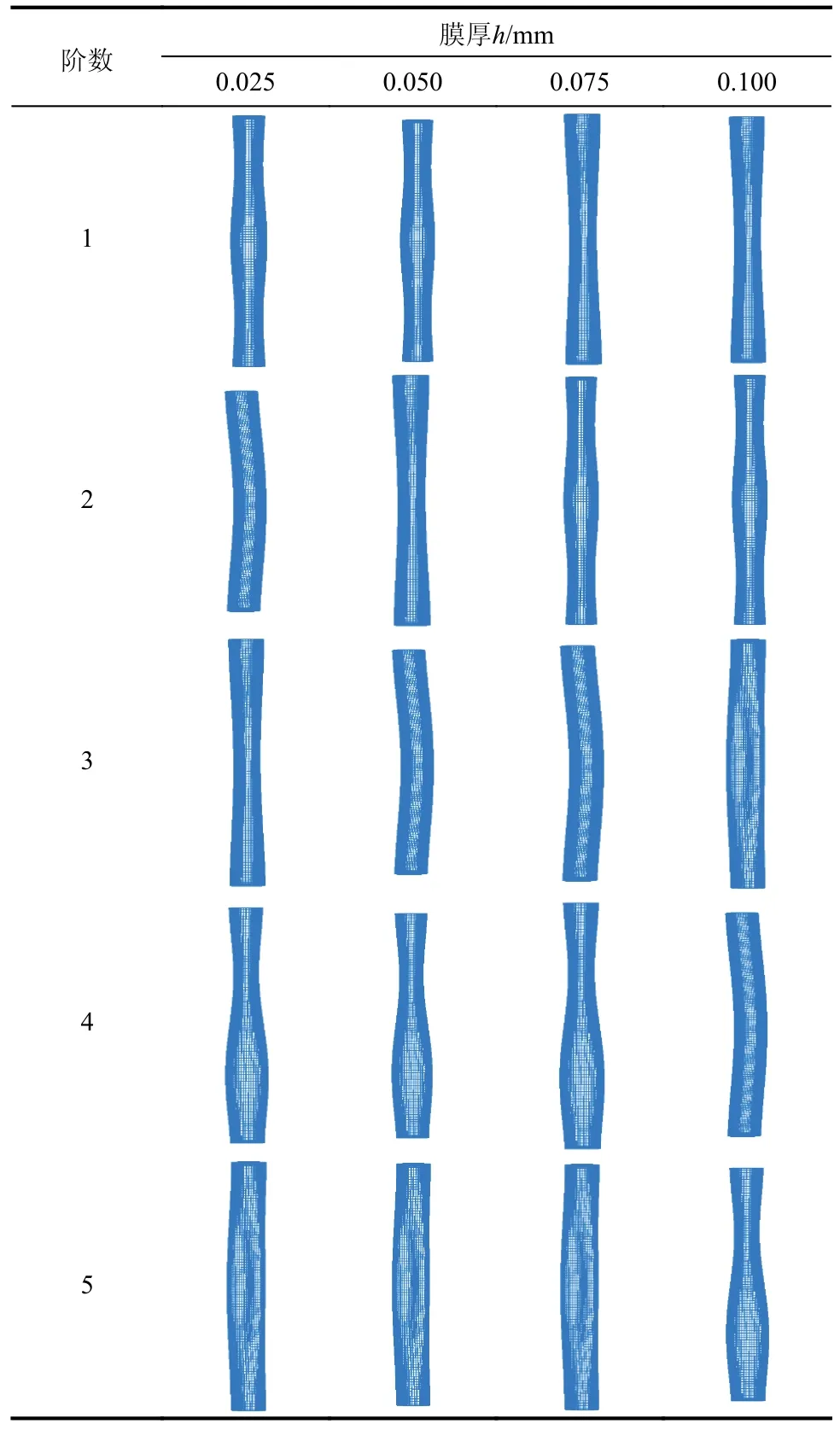
表9 不同膜厚情況下前5 階自振模態Table 9 The first five modal shapes for different membrane thickness

從表9 可以看出，膜厚對充氣薄膜管自振模態出現階次的影響較為顯著。隨著膜厚的增加，中間鼓凸的自振模態從膜厚h≤0.050 mm 的第1 階推后到h≥0.075 mm 的第2 階；整體彎曲模態從膜厚h=0.025 mm 的第2 階推后到 0.050 mm≤h≤0.075 mm 的第3 階以及h≥0.100 mm 的第4 階；中間凹陷的自振模態從h=0.025 mm 的第3 階提前到h=0.050 mm 的第2 階以及h≥0.075 mm 的第1 階；充氣薄膜管上部凹陷而下部鼓凸的自振模態從h≤0.075 mm 的第4 階推后到h≥0.100 mm 第5 階；中間局部鼓凸的自振模態從h≤0.075 mm 的第5 階提前到h≥0.100 mm 第3 階。

圖9 給出了模型M1 和模型M2 的前5 階頻率分別與模型M3 相應階次頻率的比值隨膜厚的變化情況。

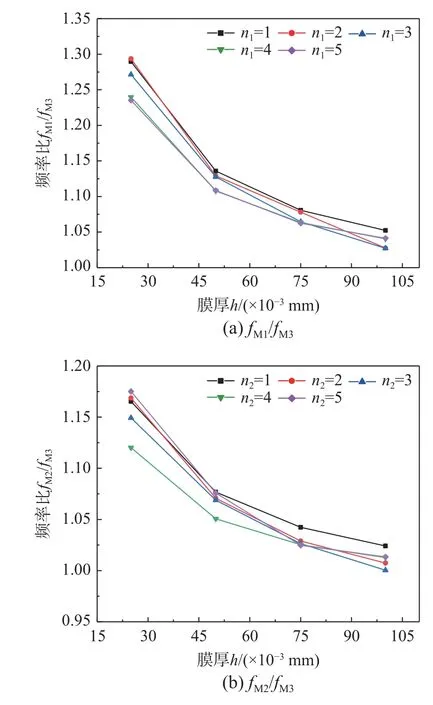
圖9 不同膜厚情況下的頻率比值Fig.9 Ratios of frequencies for different membrane thickness

從圖9(a)和圖9(b)可以看出，模型M2 由于考慮了內充氣體附加質量的影響，所以相同膜厚情況下的自振頻率低于模型M1 的相應頻率，與模型M3 的頻率差異小于模型M1 和模型M3 的頻率差異。頻率比值fM2/fM3與fM1/fM3平均相差約為5.75%，可見內充氣體附加質量對充氣薄膜管的自振頻率的影響較小。而氣-膜耦合作用影響則較為顯著，模型M1 和模型M2 的自振頻率與模型M3的自振頻率平均相差分別為12.38%和6.63%。

隨著膜厚的增加，剛度Km增大，但內充氣壓和體積均未發生改變，所以Kami不變，因而在對頻率的影響作用中，Km影響所占比重明顯增大，Kami影響所占比重顯著減小。因此，fM1/fM3和fM2/fM3的頻率比值呈現如圖9 所示的變化特征，即均隨膜厚而減小。當膜厚h<0.075 mm 時氣-膜耦合作用對自振頻率的影響作用仍然處于顯著的地位，但當膜厚h≥0.075 mm 后，氣-膜耦合作用的影響可以不用考慮。

4.4 隨端部約束的變化

對不同端部約束情況下的充氣薄膜管進行模態分析，研究氣-膜耦合作用隨端部約束類型的變化規律。端部約束考慮了兩端固定，一端固定一端簡支以及兩端均簡支的情況，其他參數同4.1 節。表10 給出了模型M3 的前5 階自振模態。

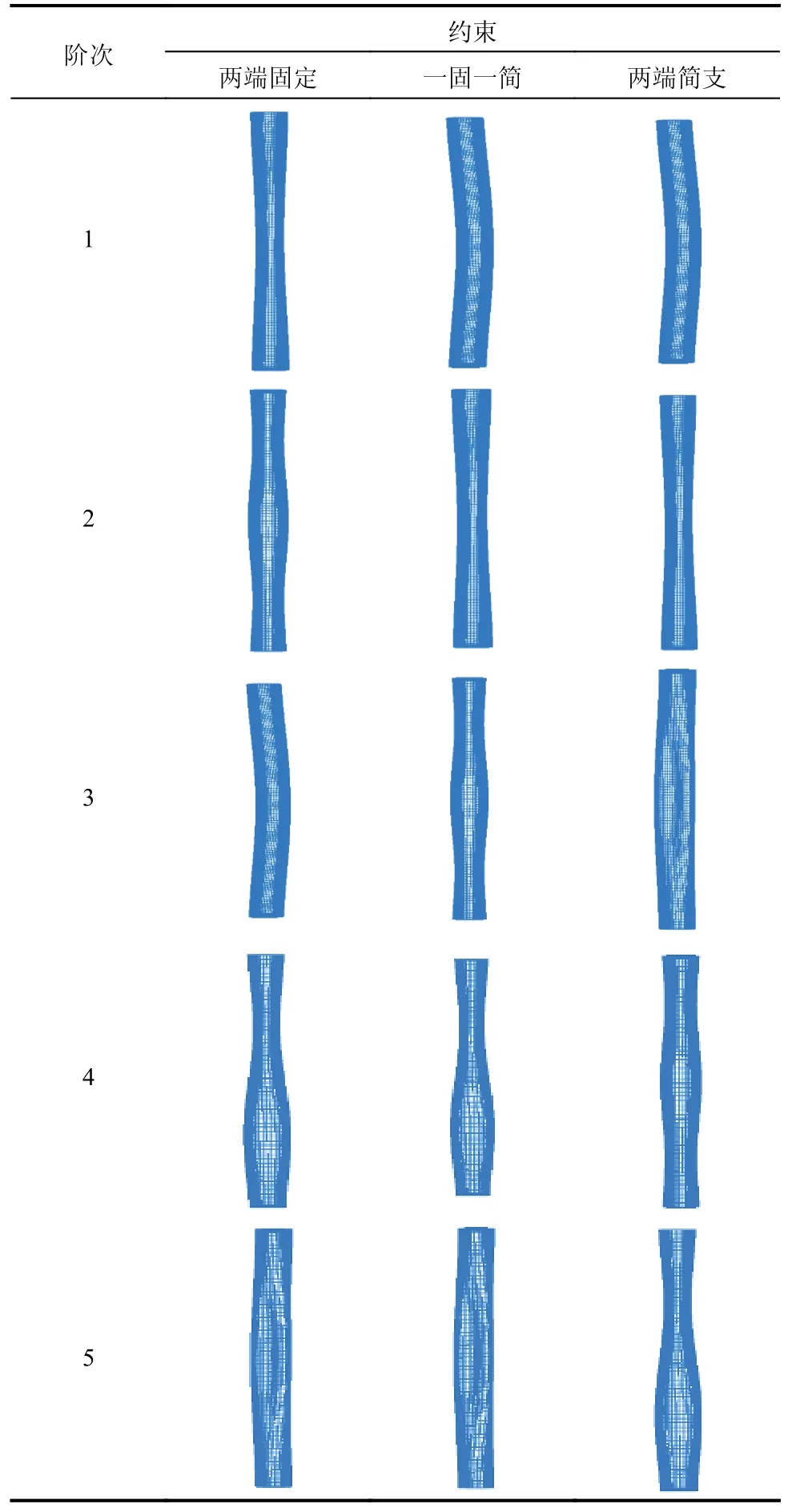
表10 不同端部約束情況下前5 階自振模態Table 10 The first five modal shapes for different end constraints

從表10 可以看出，端部約束強弱對充氣薄膜管自振模態出現階次的影響較為顯著。隨著端部約束的減弱，中部凹陷的自振模態從兩端固定時的第1 階推后到一端固定一端簡支以及兩端簡支時的第2 階；中部鼓凸的自振模態從兩端固定時的第2 階推后到一端固定一端簡支時的第3 階以及兩端簡支時的第4 階；整體彎曲自振模態從兩端固定時的第3 階提前到一端固定一端簡支以及兩端簡支時的第1 階；上部凹陷下部鼓凸的自振模態從兩端固定以及一端固定一端簡支時的第4 階推后到兩端簡支時的第5 階；中間局部鼓凸的自振模態從兩端固定以及一端固定一端簡支時的第5 階提前到兩端簡支時的第3 階。

圖10 給出了模型M1 和模型M2 的前5 階頻率分別與模型M3 相應階次頻率的比值隨端部約束程度的變化情況。

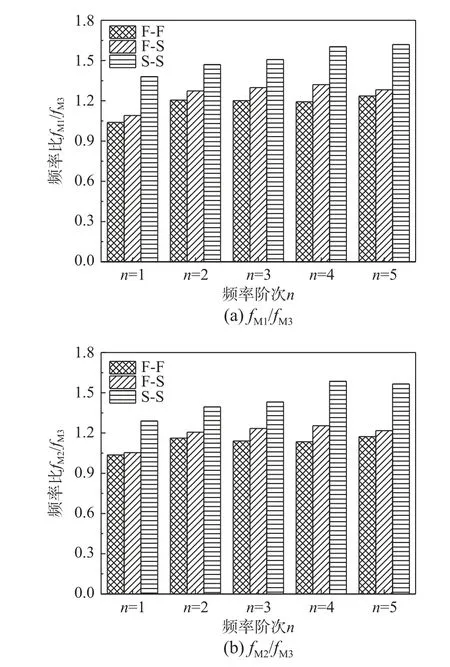
圖10 不同端部約束情況下的頻率比值Fig.10 Ratios of frequencies for different end constraints

從圖10(a)和圖10(b)可以看出，模型M2 由于考慮了內充氣體附加質量的影響，相同端部約束情況下的自振頻率低于模型M1 的相應頻率，與模型M3 的頻率差異略小于模型M1 和模型M3的頻率差異。頻率比值fM2/fM3與fM1/fM3平均相差約為5.62%。可見，內充氣體的附加質量有一定的影響，但不顯著。

隨著約束程度的減弱，模型M1、模型M2 的頻率與模型M3 的頻率的差異增大，從17.50%(模型M1)和12.93%(模型M2)分別增大到51.63%和45.38%。這意味著，氣-膜耦合作用對充氣薄膜管頻率的影響隨約束程度的減弱而逐漸增強。

隨著約束程度的減弱，剛度Km減小，但內充氣壓和體積均未發生改變，所以Kami不變，因而在對頻率的影響作用中，Km影響所占比重逐漸減小，Kami影響所占比重顯著增大。因此，fM1/fM3和fM2/fM3的頻率比值呈現如圖10 所示的變化特征，即均隨約束程度的減弱而增大。

5 結論

本文通過對充氣薄膜管在不同內充氣體作用等效方式下的動力特性進行有限元分析，研究了氣-膜耦合作用對其自振特性的影響及其隨初始內壓、長細比、膜厚以及端部約束情況的變化規律。取得的主要結論如下：

(1) 氣-膜耦合作用以及內充氣體的附加質量對充氣薄膜管的低階自振模態沒有影響，但初始內壓、長細比、膜厚以及端部約束程度的變化會影響同一模態出現的階次；氣-膜耦合作用對自振頻率有較顯著的影響作用，而內充氣體的附加質量對自振頻率的影響較小。

(2) 隨著初始內壓P0的增加，當P0≤4 kPa 時，氣-膜耦合作用影響的變化較為平緩，而當P0>4 kPa后氣-膜耦合作用影響呈現出因頻率階次不同而不同的規律：對第1 階頻率的影響逐漸降低，而對第2 階～第5 階頻率的影響則顯著增大，但在P0≥8 kPa后影響作用基本保持穩定。

(3) 隨著長細比的增加，氣-膜耦合作用的影響同樣也表現出因頻率階次不同而不同的規律：對第1 階自振頻率影響未見明顯變化，但對第2 階～第5 階自振頻率的影響則迅速增大。

(4) 隨著膜厚的增加，氣-膜耦合作用的影響快速降低。當膜厚h<0.075 mm 時，氣-膜耦合作用仍然處于較顯著的地位，但當膜厚h≥0.075 mm后，氣-膜耦合作用的影響很小。

(5) 隨著端部約束程度的減弱，氣-膜耦合作用對充氣薄膜管自振頻率的影響呈現逐漸增強的變化規律。

本文的研究揭示了氣-膜耦合作用對充氣薄膜管自振特性的影響規律，有助于深入認識充氣薄膜管的動力行為以及動力展開性能，保證充氣薄膜結構設計計算的合理性和可靠性。