采用BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化的振動(dòng)信號(hào)壓縮感知方法
朱一凱,陳安妮,余哲帆,萬(wàn)華平
(1.東南大學(xué)混凝土及預(yù)應(yīng)力混凝土結(jié)構(gòu)教育部重點(diǎn)實(shí)驗(yàn)室,江蘇 南京 211189;2.浙江大學(xué)建筑工程學(xué)院,浙江 杭州 310058)
引言
結(jié)構(gòu)健康監(jiān)測(cè)已成為土木工程結(jié)構(gòu)損傷演化行為研究的有效手段和服役安全保障的重要技術(shù)。結(jié)構(gòu)健康監(jiān)測(cè)是利用傳感技術(shù)實(shí)時(shí)監(jiān)測(cè)結(jié)構(gòu)響應(yīng)和環(huán)境變量,運(yùn)用信號(hào)處理方法提取反映結(jié)構(gòu)健康狀態(tài)的特征量,進(jìn)而對(duì)結(jié)構(gòu)的服役狀況進(jìn)行評(píng)估[1]。新興的無(wú)線傳感網(wǎng)絡(luò)技術(shù)具有成本低廉、安裝維護(hù)方便、布點(diǎn)規(guī)模大、干擾性小等優(yōu)點(diǎn),逐漸被應(yīng)用于大型土木結(jié)構(gòu)的健康監(jiān)測(cè)[2]。無(wú)線健康監(jiān)測(cè)系統(tǒng)受傳感器電池壽命、節(jié)點(diǎn)存儲(chǔ)空間和傳輸帶寬限制,難以進(jìn)行長(zhǎng)期、高頻的數(shù)據(jù)采集工作。因此,尋求一種高效率的采樣方法對(duì)于無(wú)線健康監(jiān)測(cè)系統(tǒng)非常必要,有望解決無(wú)線傳感網(wǎng)絡(luò)的能耗問(wèn)題,提升無(wú)線健康監(jiān)測(cè)系統(tǒng)的工作壽命。
壓縮感 知(Compressive Sensing,CS)[3]是一種新型采樣理論,其利用信號(hào)的稀疏特性,通過(guò)少量的采樣數(shù)據(jù)恢復(fù)出原始信號(hào)。CS 廣泛運(yùn)用于圖像處理、雷達(dá)成像及核磁共振等領(lǐng)域[4-5]。在結(jié)構(gòu)健康監(jiān)測(cè)領(lǐng)域,CS 也逐漸得到研究人員的關(guān)注。Bao 等[6-7]使用CS 對(duì)山東濱州黃河大橋的健康監(jiān)測(cè)數(shù)據(jù)進(jìn)行分析,指出原始信號(hào)自身的稀疏性是成功實(shí)現(xiàn)CS的關(guān)鍵因素,而結(jié)構(gòu)監(jiān)測(cè)信號(hào)自身稀疏性往往有限。Yao 等[8]基于模擬退火算法和蟻群算法,探究了基于CS 的傳感器布置方法,仿真和實(shí)測(cè)數(shù)據(jù)驗(yàn)證了該布置方法有效性。李惠等[9]將隨機(jī)解調(diào)器植入傳感器,用于產(chǎn)生隨機(jī)采樣矩陣,節(jié)省了傳感器內(nèi)存空間。Wan 等[10]基于時(shí)移策略構(gòu)造特殊稀疏字典,適用于風(fēng)速信號(hào)壓縮與重構(gòu),并利用杭州東站屋面實(shí)測(cè)風(fēng)速信號(hào)驗(yàn)證了該方法有效性。
對(duì)于實(shí)測(cè)信號(hào),噪聲污染不可避免,噪聲污染會(huì)導(dǎo)致原始信號(hào)的稀疏性降低,而信號(hào)稀疏性又是影響CS 效果的重要因素。針對(duì)信號(hào)噪聲問(wèn)題,Deanna 等[11]提出了CoSaMP 算法,采用回溯策略來(lái)降低噪聲干擾影響,但該方法效果對(duì)原始信號(hào)(無(wú)噪聲污染)的稀疏性要求較高。Ji 等[12]和Huang 等[13]提出了多任務(wù)貝葉斯壓縮感知方法,通過(guò)納入噪聲先驗(yàn)信息來(lái)降低噪聲干擾,該方法依賴于信號(hào)相關(guān)性且計(jì)算較為復(fù)雜。康杰等[14]基于Polar 插值的改進(jìn)正交匹配追蹤恢復(fù)算法,能夠重構(gòu)稀疏性較低的信號(hào),但該方法主要適用于頻率泄漏引起的低稀疏性情況。
本文針對(duì)受噪聲干擾且稀疏性較低的信號(hào),提出利用反向傳播(Back Propagation,BP)神經(jīng)網(wǎng)絡(luò)對(duì)LASSO 算法得到的稀疏系數(shù)進(jìn)行優(yōu)化,用于改善CS 效果。BP 神經(jīng)網(wǎng)絡(luò)將預(yù)期樣本和輸出樣本的誤差進(jìn)行反向傳播,通過(guò)反復(fù)迭代訓(xùn)練,得到優(yōu)化的稀疏系數(shù)。本文提出了基于BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化的CS方法,可有效提升信號(hào)重構(gòu)的精度,通過(guò)仿真數(shù)據(jù)和實(shí)測(cè)數(shù)據(jù)驗(yàn)證了該方法的有效性。
1 壓縮感知基本理論
原始信號(hào)x∈RN經(jīng)過(guò)觀測(cè)矩陣Φ∈RM×N壓縮觀測(cè),可以得到觀測(cè)信號(hào)y∈RM,如下:
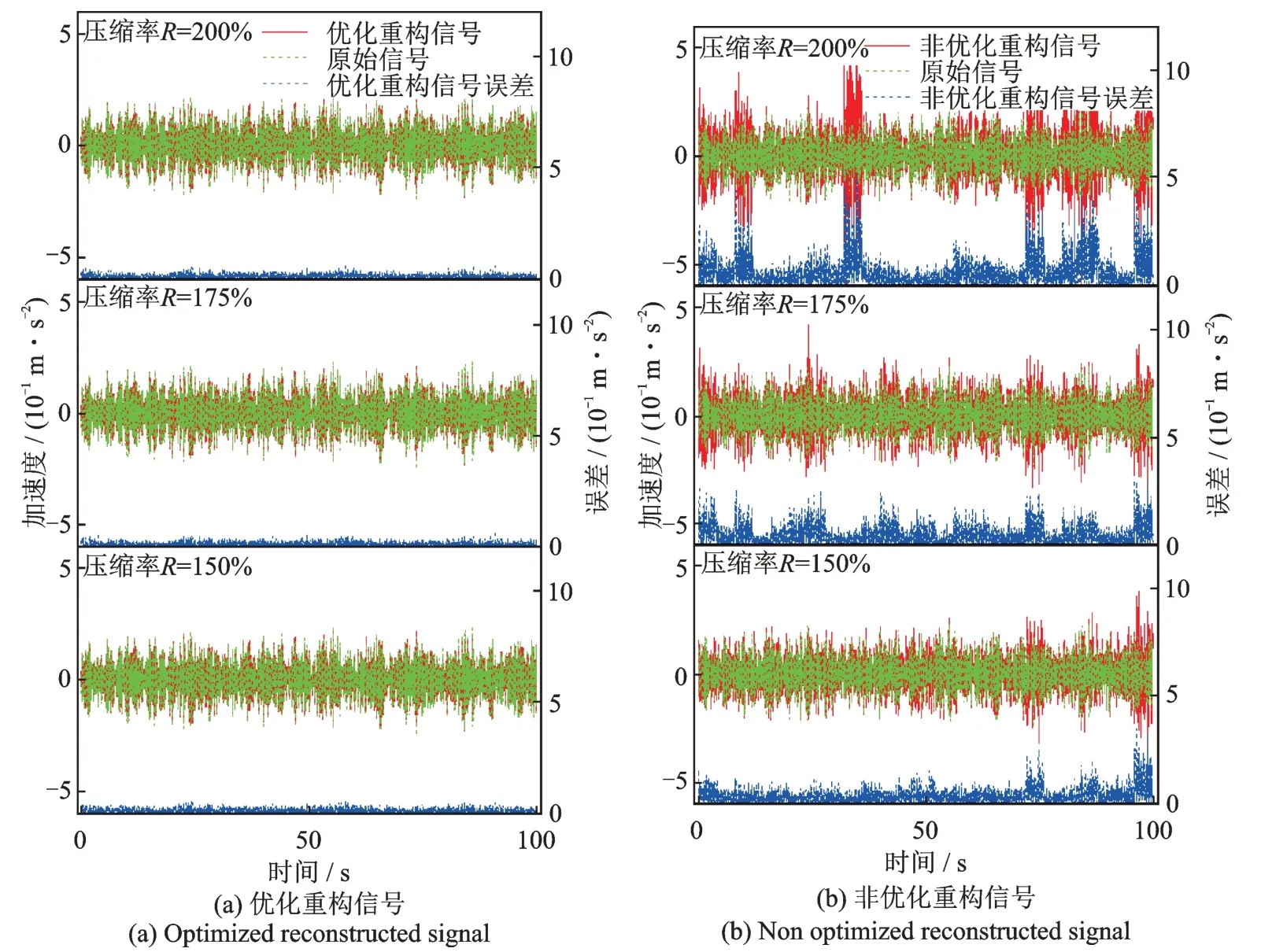
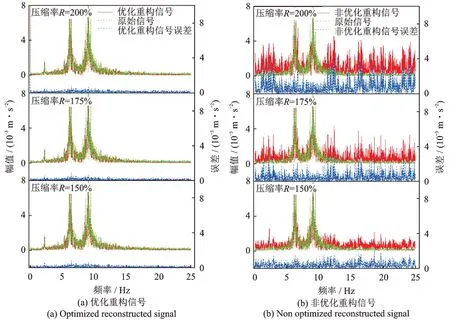
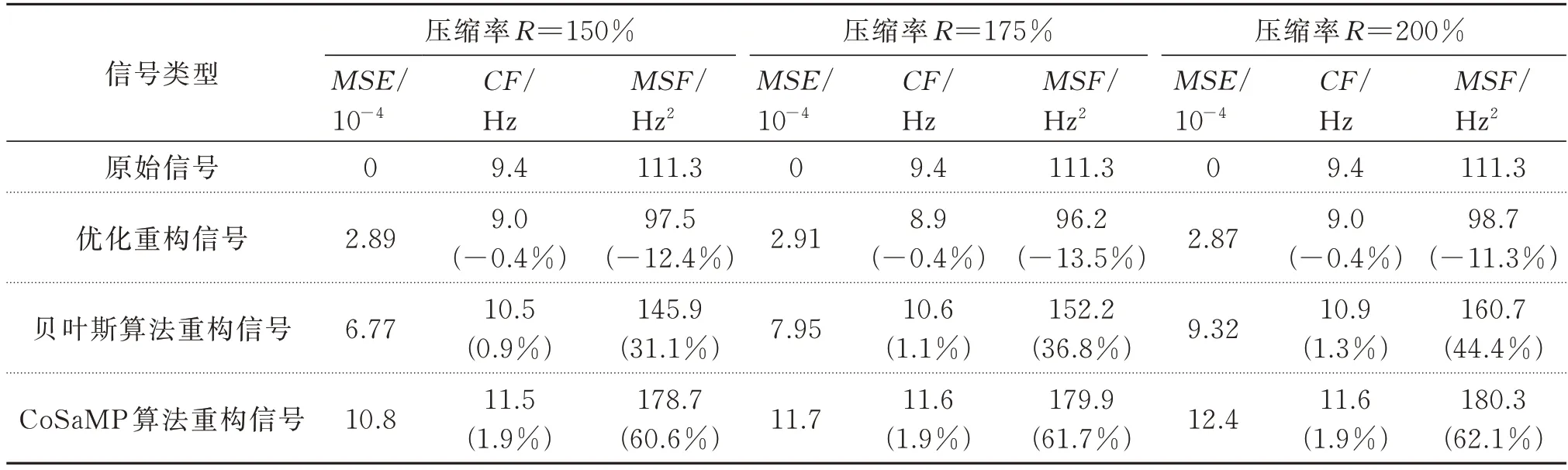
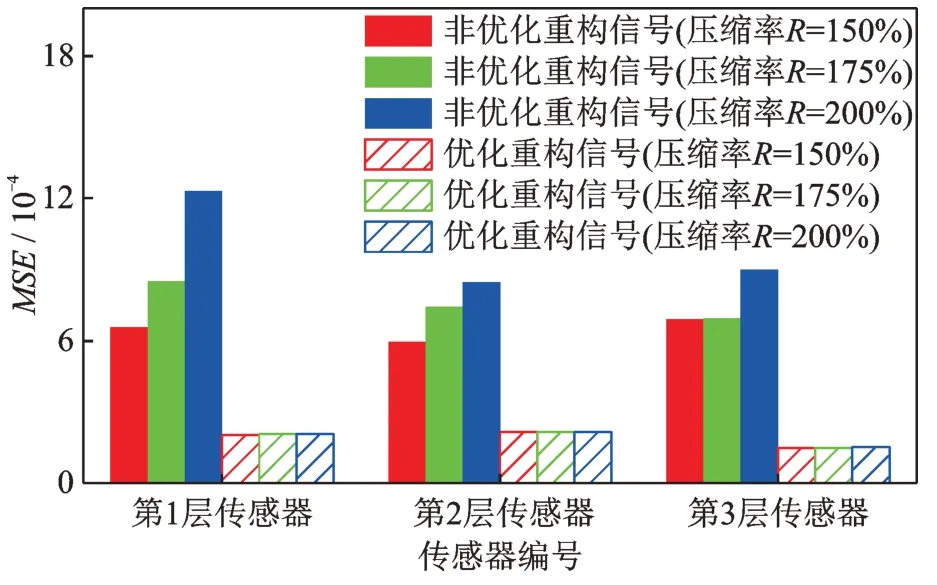
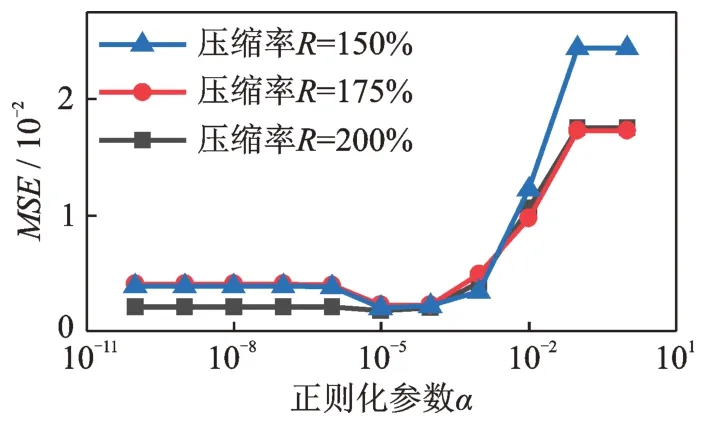
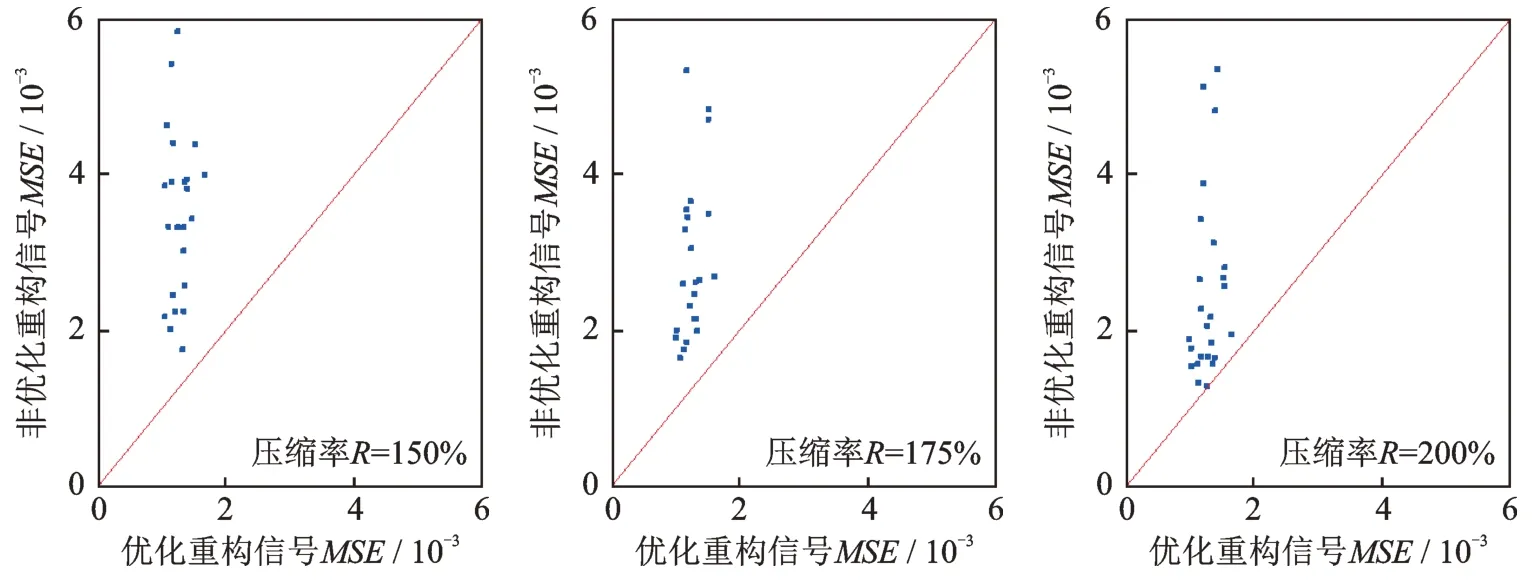
式中M和N的取值滿足M 式中w為稀疏表示的系數(shù)向量。由式(2)可得: 將式(3)代入式(1),令傳感矩陣A=ΦΨ,有: 根據(jù)方程(4),壓縮感知問(wèn)題可描述為:已知觀測(cè)信號(hào)y和傳感矩陣A,在w具有稀疏性的先驗(yàn)條件下,求解w。式(4)的求解可以轉(zhuǎn)化為求解下式表示的l0范數(shù)問(wèn)題: 式中‖·‖0為l0偽范數(shù),表示向量中非零值的個(gè)數(shù)。 Candès 等[15]指出傳感矩陣A滿足有限等距性條件(Restricted Isometry Property,RIP)時(shí): 式(4)可以解得唯一的稀疏解;當(dāng)觀測(cè)矩陣Φ為伯努利隨機(jī)矩陣時(shí),傳感矩陣A通常可以滿足RIP條件。且式(5)可以轉(zhuǎn)變?yōu)榍蠼庀率降膌1范數(shù)最小化問(wèn)題: 式中‖·‖1為l1范數(shù),表示向量各個(gè)分量的絕對(duì)值之和。 式(7)可使用LASSO 算法通過(guò)最小化方差來(lái)求解: 式中α為正則化參數(shù),用來(lái)控制w的稀疏度,避免LASSO 算法出現(xiàn)過(guò)擬合的情況。 式(8)是連續(xù)的凸函數(shù),可以通過(guò)迭代求解,解得稀疏系數(shù)w的估計(jì)值,通過(guò)式(3)計(jì)算得到信號(hào)的估計(jì)值。 若x為一加速度信號(hào),在離散余弦基(DCT)上的表示具有“能量集中”的特性,稀疏性較好,通常DCT 選為變換基Ψ∈RN×N。 考慮到實(shí)測(cè)的加速度信號(hào)往往含有噪聲,式(3)中引入了噪聲項(xiàng)ε,得到: 將噪聲 項(xiàng)ε在DCT上用系數(shù)向量wε表示,則式(9)轉(zhuǎn)變?yōu)椋?/p> 在信號(hào)傳輸過(guò)程中,傳統(tǒng)方法傳輸完整原始信號(hào)x,未進(jìn)行信號(hào)壓縮。而CS 傳輸方法是將原始信號(hào)x乘以觀測(cè)矩陣Φ得到壓縮信號(hào)y,然后將壓縮信號(hào)進(jìn)行傳輸,實(shí)現(xiàn)數(shù)據(jù)壓縮傳輸效果;在接收傳輸數(shù)據(jù)后,再求解系數(shù)向量(w+wε),并重構(gòu)原始加速度信號(hào)x。但此時(shí)系數(shù)向量因受噪聲干擾而稀疏性下降,利用LASSO 算法得到的解為粗略稀疏系數(shù)。為了降低噪聲的干擾影響和提升壓縮感知效果,在粗略稀疏系數(shù)和精確稀疏系數(shù)之間建立一個(gè)映射,采用BP 神經(jīng)網(wǎng)絡(luò)建立此映射。BP 神經(jīng)網(wǎng)絡(luò)具有極強(qiáng)的非線性映射能力,并適合處理大量復(fù)雜數(shù)據(jù),具有得到接近精確稀疏系數(shù)的優(yōu)化稀疏系數(shù)的潛力。 BP 神經(jīng)網(wǎng)絡(luò)如圖1 所示,通常由輸入層、隱含層、輸出層3 個(gè)部分組成,每一層由若干神經(jīng)元組成,層與層之間的神經(jīng)元全數(shù)相連。神經(jīng)元的輸入是上一層神經(jīng)元的輸出,加權(quán)求和后加上閾值,代入激活函數(shù),得到的輸出傳入下一層神經(jīng)元。其對(duì)應(yīng)的數(shù)學(xué)模型為: 圖1 BP 神經(jīng)網(wǎng)絡(luò)及神經(jīng)元結(jié)構(gòu)Fig.1 BP neural network and neuron structure 式中pi為前一層中第i個(gè)神經(jīng)元的輸入;wi為對(duì)應(yīng)的權(quán)值;n為前一層神經(jīng)元的個(gè)數(shù);b為該神經(jīng)元的閾值;f(·)表示激活函數(shù)。 構(gòu)建神經(jīng)網(wǎng)絡(luò)是一個(gè)循環(huán)迭代過(guò)程,不斷調(diào)整和更新神經(jīng)元的權(quán)值和閾值,直到輸出值和目標(biāo)值之間的誤差滿足要求,達(dá)到滿意的擬合效果[16]。神經(jīng)網(wǎng)絡(luò)的輸出值和目標(biāo)值誤差用均方誤差定義,如下式所示: 式中ER(θ)為目標(biāo)誤差;wi為第i個(gè)權(quán)值參數(shù);bi為第i個(gè)閾值參數(shù);K為訓(xùn)練樣本集中的樣本個(gè)數(shù);ξj為第j個(gè)目標(biāo)量為第j個(gè)輸出量;N為目標(biāo)量的長(zhǎng)度。 神經(jīng)網(wǎng)絡(luò)的優(yōu)化問(wèn)題轉(zhuǎn)變成求ER(θ)最小值的問(wèn)題,使用ADAM 優(yōu)化算法[17]求解。ADAM 通過(guò)計(jì)算梯度的一階矩和二階矩估計(jì),動(dòng)態(tài)調(diào)整針對(duì)每個(gè)參數(shù)的學(xué)習(xí)率。其迭代式如下: 式中參數(shù)0≤β1<1,0 ≤β2<1,分別取0.9 和0.999。 本文方法結(jié)合了LASSO 算法和BP 神經(jīng)網(wǎng)絡(luò),前者用于尋找初始稀疏系數(shù),后者優(yōu)化初始稀疏系數(shù)。LASSO 算法的目標(biāo)是尋找稀疏系數(shù)中所有非零元素,但由于噪聲干擾,能夠較為準(zhǔn)確地識(shí)別出稀疏系數(shù)中數(shù)值較大的非零元素。對(duì)于數(shù)值較小的非零元素,LASSO 算法求解精度較低,但數(shù)值較小的非零元素和數(shù)值較大的元素具有一定的相關(guān)性。LASSO 算法求解出初始稀疏系數(shù)和精確稀疏系數(shù),其中較為精確的數(shù)值較大的非零元素與數(shù)值較小的元素具有一定的相關(guān)性。由于噪聲的隨機(jī)性較強(qiáng),難以高效精確描述數(shù)值大元素與數(shù)值小元素間的相關(guān)性,為此根據(jù)初始稀疏系數(shù)來(lái)求解精確稀疏系數(shù)。而B(niǎo)P 神經(jīng)網(wǎng)絡(luò)具有極強(qiáng)的非線性映射能力,能夠通過(guò)訓(xùn)練尋找初始稀疏系數(shù)和精確稀疏系數(shù)之間的非線性擬合關(guān)系,對(duì)初始稀疏系數(shù)優(yōu)化,使其更加接近精確稀疏系數(shù),達(dá)到優(yōu)化重構(gòu)精度的效果。 為了避免神經(jīng)網(wǎng)絡(luò)泛化能力受稀疏系數(shù)幅值大小影響,對(duì)稀疏系數(shù)進(jìn)行線性歸一化。對(duì)粗略稀疏系數(shù)及其對(duì)應(yīng)稀疏系數(shù)歸一化方法如下所示: 需對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練,預(yù)采集一段完整信號(hào),分為K段長(zhǎng)度為N的信號(hào)。根據(jù)式(2)和(15)計(jì)算得到歸一化后的精確稀疏系數(shù)樣本集為了消除稀疏系數(shù)幅值大小影響,對(duì)其進(jìn)行線性歸一化后再作為神經(jīng)網(wǎng)絡(luò)的目標(biāo)輸出;使用LASSO 算法得到粗略稀疏系數(shù)樣本集,作為神經(jīng)網(wǎng)絡(luò)的輸入,得到神經(jīng)網(wǎng)絡(luò)的實(shí)際輸出為歸一化的優(yōu)化稀疏系數(shù)。利用ADAM 優(yōu)化算法得到模型參數(shù),建立BP神經(jīng)網(wǎng)絡(luò)。BP 神經(jīng)網(wǎng)絡(luò)訓(xùn)練完成后,采用新的壓縮數(shù)據(jù)用來(lái)測(cè)試,對(duì)比粗略稀疏系數(shù)和優(yōu)化稀疏系數(shù)的重構(gòu)效果,以檢驗(yàn)該方法有效性。優(yōu)化稀疏系數(shù)的計(jì)算流程如圖2 所示。 圖2 稀疏系數(shù)優(yōu)化的計(jì)算流程Fig.2 Calculation process of sparse coefficient optimization 用三層框架結(jié)構(gòu)(如圖3 所示)驗(yàn)證本文方法的有效性。每層樓板的質(zhì)量表示為mi(i=1,2,3),每層樓的剛度系數(shù)為ki,阻尼系數(shù)為ci。每層樓板的質(zhì)量、剛度系數(shù)、阻尼器系數(shù)分別為10 kg,1000 kg/m和10 N·s/m。則該三層框架結(jié)構(gòu)的質(zhì)量矩陣Μ、剛度矩陣K和阻尼矩陣C分別為: 圖3 三層框架結(jié)構(gòu)模型Fig.3 Structural model of three story frame 假設(shè)在每層樓板均裝有加速度傳感器,且傳感器的采樣頻率設(shè)為50 Hz,采樣持續(xù)時(shí)間為300 s。為了模擬結(jié)構(gòu)振動(dòng)響應(yīng),每層施加高斯噪聲激勵(lì)N(0,0.01);同時(shí)考慮測(cè)試噪聲影響,計(jì)算得到的振動(dòng)響應(yīng)加入高斯噪聲N(0,0.001)。仿真模擬采用的電腦計(jì)算平臺(tái)是:Windows10 操作系統(tǒng)/Intel Core i7-9750H CPU/16G RAM,及數(shù)值軟件是:Python 3.9+numpy 1.21.1+scipy 1.7.1。得到的樓板加速度信號(hào)如圖4 所示。 圖4 各層加速度信號(hào)采樣值Fig.4 Sampling value of acceleration signal of each layer 定義采樣率R=N/M,單次運(yùn)算截取出長(zhǎng)度N=200 的一維時(shí)間序列進(jìn)行運(yùn)算,對(duì)R=150%,175%,200%三種不同壓縮率的情況進(jìn)行討論。在利用神經(jīng)網(wǎng)絡(luò)對(duì)粗略稀疏系數(shù)進(jìn)行優(yōu)化之前,需選取合適的LASSO 算法的正則化參數(shù)α,得到精度較好的稀疏系數(shù),利于后續(xù)BP 神經(jīng)網(wǎng)絡(luò)對(duì)稀疏系數(shù)進(jìn)行優(yōu)化。 采用均方誤差MSE=指標(biāo)來(lái)評(píng)價(jià)重構(gòu)信號(hào)的精度,其中K表示信號(hào)的段數(shù)。α依次取100,10-1,10-2,…,10-10,選用前1000 個(gè)數(shù)據(jù)來(lái)進(jìn)行壓縮感知和重構(gòu),計(jì)算結(jié)果如圖5 所示。可知,當(dāng)α=10-5時(shí),LASSO 算法能夠得到較高精度的粗略稀疏系數(shù)。 圖5 不同壓縮率情況下的均方誤差與正則化參數(shù)的關(guān)系(框架結(jié)構(gòu)模型)Fig.5 Relationship between MSE and regularization parameters under different compression rates(frame structure model) 前10199 個(gè)采樣點(diǎn)通過(guò)步長(zhǎng)為1、長(zhǎng)度為200 的滑動(dòng)窗構(gòu)成10000 個(gè)N=200 的信號(hào)樣本,生成10000 個(gè)精確稀疏系數(shù)樣本和粗略稀疏系數(shù)樣本。將得到的精確稀疏系數(shù)樣本和粗略稀疏系數(shù)樣本劃分為10 組,每組有1000 個(gè)粗略稀疏系數(shù)樣本及其對(duì)應(yīng)的精確稀疏系數(shù)樣本。前9 組數(shù)據(jù)用作訓(xùn)練集對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練,第10 組數(shù)據(jù)作為驗(yàn)證集,判斷出合適的迭代次數(shù)。根據(jù)式(12)定義本文方法的目標(biāo)誤差ER=用于評(píng)價(jià)訓(xùn)練后的神經(jīng)網(wǎng)絡(luò)擬合精度。神經(jīng)網(wǎng)絡(luò)設(shè)置1 層隱藏層,輸入、輸出信號(hào)長(zhǎng)度均為200,避免神經(jīng)網(wǎng)絡(luò)內(nèi)部傳遞信息出現(xiàn)丟失或者冗余,將其神經(jīng)元數(shù)量設(shè)置為200;初始學(xué)習(xí)率η設(shè)置為10-4。圖6 展示了150%,175%,200%三種壓縮率下在不同迭代次數(shù)下的目標(biāo)誤差ER。 圖6 不同壓縮率情況下的目標(biāo)誤差與迭代次數(shù)的關(guān)系(框架結(jié)構(gòu)模型)Fig.6 Relationship between target error and iteration times under different compression rates(frame structure model) 由圖6 可知,當(dāng)?shù)螖?shù)為4400 時(shí),目標(biāo)誤差ER達(dá)到較小值,隨著迭代次數(shù)繼續(xù)增加,目標(biāo)誤差ER逐漸增大,因此迭代次數(shù)為4400 時(shí)的BP 神經(jīng)網(wǎng)絡(luò)的效果最佳。選擇長(zhǎng)度為5000 時(shí)的加速度信號(hào)作為測(cè)試集,將其分為25 段,每段N=200。對(duì)于測(cè)試集,利用上述方法得到粗略稀疏系數(shù)和優(yōu)化稀疏系數(shù),基于兩種稀疏系數(shù)來(lái)重構(gòu)信號(hào),并計(jì)算各自的均方誤差MSE,對(duì)比結(jié)果如圖7所示。從圖7中可以看出,本文方法得到的重構(gòu)信號(hào)與原始信號(hào)的誤差相對(duì)更小。 圖7 重構(gòu)信號(hào)優(yōu)化前后的誤差對(duì)比(框架結(jié)構(gòu)模型)Fig.7 Error comparison before and after optimization of reconstructed signal(frame structure model) 為更加直觀展示重構(gòu)效果,將重構(gòu)出的時(shí)域信號(hào)和頻域信號(hào)及其誤差展示在圖8 和9 中。從圖8和9 中可以看出,對(duì)于第1 層樓板的加速度信號(hào),優(yōu)化稀疏系數(shù)重構(gòu)出的信號(hào)與原始信號(hào)之間的偏差在時(shí)域和頻域都更小。 圖8 重構(gòu)加速度信號(hào)在時(shí)域內(nèi)對(duì)比結(jié)果(第1 層傳感器)Fig.8 Comparison results of reconstructed acceleration signal in time domain(layer 1 sensor) 圖9 重構(gòu)加速度信號(hào)在頻域內(nèi)對(duì)比結(jié)果(第1 層傳感器)Fig.9 Comparison results of reconstructed acceleration signal in frequency domain(layer 1 sensor) 為了更全面展示本文重構(gòu)方法的性能,將第1層優(yōu)化重構(gòu)信號(hào)與貝葉斯算法和CoSaMP 算法重構(gòu)信號(hào)進(jìn)行對(duì)比。采用誤差指標(biāo)MSE衡量重構(gòu)誤差,并引入頻率重心指標(biāo)CF=∑fi yi/∑yi和均方頻率MSF=∑fi2yi/∑yi表征重構(gòu)信號(hào)的頻率特征,其 中,fi表示頻 譜中第i個(gè)頻率;yi表示第i個(gè) 頻率對(duì)應(yīng)的幅值。不同算法的指標(biāo)對(duì)比結(jié)果如表1 所示。相較于其他重構(gòu)算法,使用BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化的重構(gòu)信號(hào)誤差明顯更小,并且重構(gòu)信號(hào)的頻率特征更加接近原始信號(hào)。 表1 不同算法重構(gòu)信號(hào)的誤差和頻率特征對(duì)比(第1 層傳感器)Tab.1 Comparison of error and frequency characteristics of reconstructed signals with different algorithms(layer 1 sensor) 為了更全面展示方法的可行性,對(duì)所有樓板的加速度數(shù)據(jù)進(jìn)行分析。在三種不同壓縮率的情況下,優(yōu)化前后的加速度信號(hào)重構(gòu)誤差對(duì)比結(jié)果如圖10 所示。使用BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化后,加速度信號(hào)的重構(gòu)誤差降低明顯,表明本文方法用于仿真加速度信號(hào)重構(gòu)精度高。 圖10 不同測(cè)點(diǎn)優(yōu)化前后重構(gòu)信號(hào)的誤差對(duì)比(第1~3 層傳感器)Fig.10 Error comparison of reconstructed signals before and after optimization of different measuring points(sensors of layer 1~3) 用廣州塔的實(shí)測(cè)加速度信號(hào)進(jìn)一步驗(yàn)證本文方法的有效性。廣州塔位于中國(guó)廣東省廣州市海珠區(qū),總高度600 m,其中天線桅桿高146 m,塔身主體高454 m。廣州塔的塔身主體布置了20 個(gè)加速度傳感器(如圖11 所示),采樣頻率為50 Hz。關(guān)于廣州結(jié)構(gòu)健康監(jiān)測(cè)系統(tǒng)的更詳細(xì)介紹,請(qǐng)參考文獻(xiàn)[18]和網(wǎng)站:http://www.zn903.com/ceyxia/benchmark/index.htm。 圖11 廣州塔加速度傳感器測(cè)點(diǎn)布置Fig.11 Measuring point layout of acceleration sensor of Canton tower 用廣州塔底部編號(hào)01 傳感器的加速度信號(hào)進(jìn)行深入分析,同樣考慮R=150%,175%,200%三種壓縮率情況。根據(jù)上節(jié)提到的方法構(gòu)建訓(xùn)練集、驗(yàn)證集和測(cè)試集。圖12 展示了正則化參數(shù)α和均方誤差MSE的關(guān)系,由12 圖可知,當(dāng)α取10-5時(shí),粗略稀疏系數(shù)重構(gòu)出的信號(hào)與原始信號(hào)誤差最小。圖13 展示了不同壓縮率下和不同迭代次數(shù)與目標(biāo)誤差ER的關(guān)系。由圖13 可知,當(dāng)?shù)螖?shù)取20000 時(shí),目標(biāo)誤差ER達(dá)到較小值且不再明顯減小,因此迭代次數(shù)為20000 時(shí)的BP 神經(jīng)網(wǎng)絡(luò)達(dá)到訓(xùn)練效果。 圖12 不同壓縮率情況下的均方誤差與正則化參數(shù)的關(guān)系(廣州塔)Fig.12 Relationship between MSE and regularization parameters under different compression rates(Canton tower) 圖13 不同壓縮率情況下的目標(biāo)誤差與迭代次數(shù)的關(guān)系(廣州塔)Fig.13 Relationship between target error and iteration times under different compression rates(Canton tower) 同樣地,選擇長(zhǎng)度為5000 的測(cè)試集,參照上一節(jié)的方法求得粗略稀疏系數(shù)和優(yōu)化稀疏系數(shù)信號(hào)。基于兩種稀疏系數(shù)重構(gòu)出加速度信號(hào),計(jì)算得到各自的均方誤差MSE,結(jié)果如圖14 所示。圖14 表明,優(yōu)化后得到的重構(gòu)信號(hào)的誤差更小。 圖14 重構(gòu)信號(hào)優(yōu)化前后的誤差對(duì)比(廣州塔)Fig.14 Error comparison before and after optimization of reconstructed signal(Canton tower) 為更直觀展示重構(gòu)效果,重構(gòu)加速度信號(hào)在時(shí)域和頻域的對(duì)比結(jié)果如圖15 和16 所示。由圖15 和16 可得,優(yōu)化后的重構(gòu)加速度信號(hào)與原始加速度信號(hào)之間的偏差在時(shí)域和頻域均更小。 圖15 重構(gòu)加速度信號(hào)在時(shí)域內(nèi)對(duì)比結(jié)果(傳感器編號(hào)01)Fig.15 Comparison results of reconstructed acceleration signal in time domain(sensor No.01) 圖16 重構(gòu)加速度信號(hào)在頻域內(nèi)對(duì)比結(jié)果(傳感器編號(hào)01)Fig.16 Comparison result of reconstructed acceleration signal in frequency domain(sensor No.01) 為了更全面展示本文重構(gòu)方法的性能,不同算法重構(gòu)信號(hào)的指標(biāo)對(duì)比結(jié)果如表2 所示。在三種不同壓縮率的情況下,相較于其他重構(gòu)算法,使用BP神經(jīng)網(wǎng)絡(luò)優(yōu)化的重構(gòu)信號(hào)誤差明顯更小,并且重構(gòu)信號(hào)的頻率特征更加接近原始信號(hào)。 表2 不同算法重構(gòu)信號(hào)的誤差和頻率特征對(duì)比(傳感器編號(hào)01)Tab.2 Comparison of error and frequency characteristics of reconstructed signals with different algorithms(sensor No.01) 為了更全面展示方法的可行性,用所有傳感器的加速度數(shù)據(jù)進(jìn)行分析,這里只展示重構(gòu)信號(hào)誤差的對(duì)比結(jié)果。在三種不同壓縮率的情況下,優(yōu)化前后的加速度信號(hào)重構(gòu)誤差對(duì)比結(jié)果如圖17 所示。使用BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化后,加速度信號(hào)的重構(gòu)誤差降低明顯,表明本文方法用于加速度信號(hào)重構(gòu)精度高。 圖17 不同測(cè)點(diǎn)優(yōu)化前后重構(gòu)信號(hào)的誤差對(duì)比(傳感器編號(hào)01~20)Fig.17 Error comparison of reconstructed signals before and after optimization of different measuring points(Sensor No.01~ 20) 噪聲會(huì)導(dǎo)致振動(dòng)信號(hào)的稀疏性下降,進(jìn)而影響LASSO 算法用于信號(hào)重構(gòu)的效果。本文提出了基于BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化的壓縮感知方法,利用BP 神經(jīng)網(wǎng)絡(luò)對(duì)LASSO 算法得到的稀疏系數(shù)進(jìn)行優(yōu)化,提升振動(dòng)信號(hào)的重構(gòu)精度。用三層框架結(jié)構(gòu)和廣州塔驗(yàn)證本文方法的有效性,得到的結(jié)論如下:(1)LASSO 算法的正則化參數(shù)和BP 神經(jīng)網(wǎng)絡(luò)的迭代次數(shù)是本文方法的兩個(gè)關(guān)鍵參數(shù),選擇合適的正則化參數(shù)可以獲得較高精度的稀疏系數(shù),選取合適的迭代次數(shù)可提升BP 神經(jīng)網(wǎng)絡(luò)的優(yōu)化效果。(2)相比非優(yōu)化的重構(gòu)信號(hào),基于BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化的重構(gòu)信號(hào)與原始信號(hào)之間的偏差在時(shí)域和頻域均更小,表明引入的BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化策略可有效提升壓縮感知方法的性能。2 BP 神經(jīng)網(wǎng)絡(luò)優(yōu)化方法
2.1 BP 神經(jīng)網(wǎng)絡(luò)原理

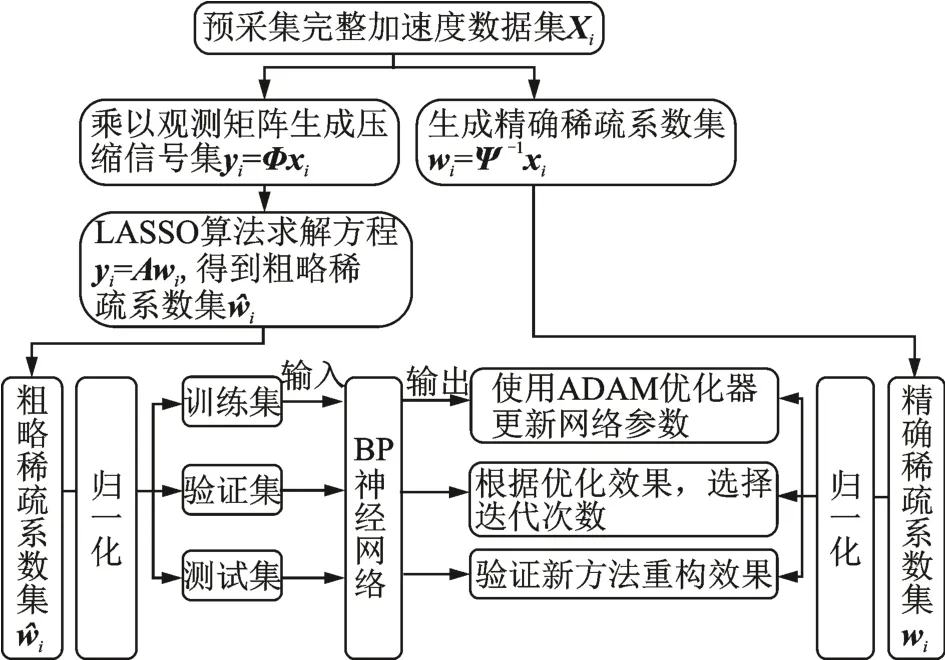
2.2 稀疏系數(shù)優(yōu)化方法
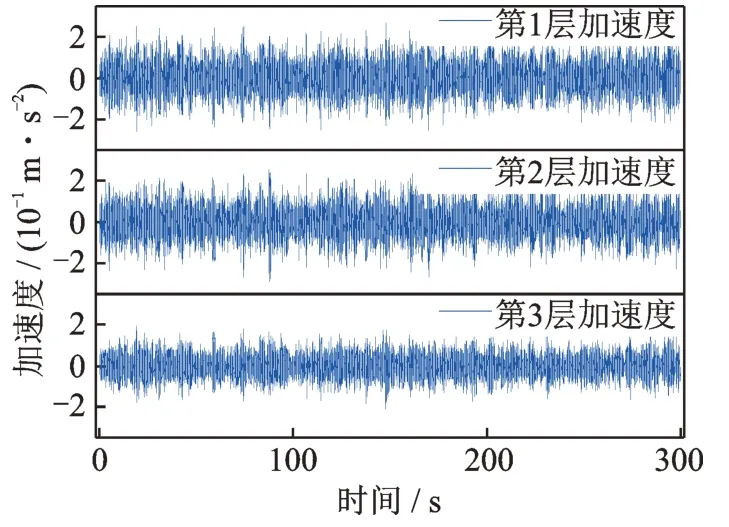
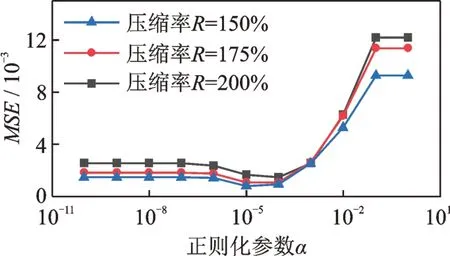
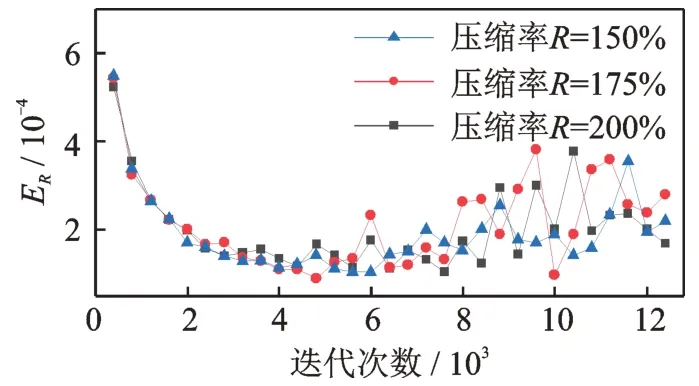
3 仿真數(shù)據(jù)驗(yàn)證


4 實(shí)測(cè)數(shù)據(jù)驗(yàn)證






5 結(jié)論
- 振動(dòng)工程學(xué)報(bào)的其它文章
- 郭永懷 不忘初心志報(bào)國(guó) 留取丹心照長(zhǎng)空
- 模型無(wú)關(guān)元遷移學(xué)習(xí)用于空間滾動(dòng)軸承壽命階段識(shí)別
- 改進(jìn)型EEMD和MSB解調(diào)方法及其在軸承故障特征提取中的應(yīng)用
- 覆水效應(yīng)的地下相干函數(shù)與相變V 形峽谷多點(diǎn)地震動(dòng)模擬及其特征規(guī)律
- 考慮臺(tái)風(fēng)空間位置的橋址區(qū)風(fēng)特性模型實(shí)測(cè)研究
- 橋梁斷面范德波爾振子渦激氣動(dòng)力模型參數(shù)非線性化的能量原理

