某空氣舵系統非線性建模及參數識別

周國峰，劉 博

（中國運載火箭技術研究院，北京 100076）

引言

空氣舵是廣泛使用的飛行器操縱機構，通過舵面偏轉產生氣動控制力，實現飛行器姿態和軌跡控制的目的，是飛行控制系統中的關鍵部件。

空氣舵系統中含有運動副，因此不可避免地存在間隙與摩擦等非線性因素。大量研究表明，間隙等非線性因素會對舵翼結構氣動彈性特性產生顯著的影響［1-7］。趙永輝等［1］研究了三自由度二維翼段系統中操縱面鉸鏈間隙導致的系統極限環振動，并發現振幅、頻率隨著來流速度增加而跳躍的現象。楊寧等［2］分析了折疊翼結構的間隙非線性顫振，發現具有初載間隙的典型折疊翼結構也會產生穩定的極限環振蕩，且結構響應與初始擾動相關。薛紅軍等［3］針對飛機操縱系統，建立了間隙的非線性接觸模型，并采用修正的庫倫摩擦模型描述間隙的摩擦作用，詳細研究了含間隙機構的動態特性。王成華等［4］建立了舵系統含間隙與摩擦的單自由度數學模型，研究了舵結構系統飛行自激振動現象的產生機理。Na 等［5］研究了折疊旋轉尾翼的超音速氣動彈性問題，發現鉸鏈間隙導致旋轉速度增加，引起顫振速度的降低；而相同轉速下，間隙非線性增強了系統氣動彈性穩定性。Kholodar［6］研究了飛機控制面及掛架間隙對顫振極限環振動量級的影響，發現隨著間隙的增加，座艙振動環境變惡劣，到一定程度會影響飛行員駕駛。胡海巖等［7］對國內外控制面間隙非線性研究進展進行了綜述，并指出控制面鉸鏈間隙非線性聯合作用下的氣動彈性控制問題是今后一個時期值得關注的問題之一。

在本文作者多年的飛行器工程研制實踐中，也同樣一直在分析解決間隙和摩擦非線性對舵系統傳遞特性的影響。如果這一問題解決不徹底就會在飛行中產生伺服彈性問題甚至氣動伺服彈性問題。為了開展針對性設計，需要建立合理的舵系統的非線性動力學模型，并通過試驗數據辨識確定模型中的所有參數。非線性系統辨識方法的研究從20 世紀70 年代開始，由最開始的單自由度系統到復雜的工程結構，得到大量學者的關注。提出了能量法［8］、頻域法［9］、基于遺傳算法［10］和等效線性化理論的各種方法［11］等。文獻［12-13］將近幾十年的相關方法分為7 類，進行了系統地綜述，指出連接環節的間隙、摩擦等非線性因素建模與參數識別是當前結構動力學領域的焦點之一。

本文以某航天飛行器空氣舵系統為研究對象，考慮運動副間隙和摩擦，采用理論與試驗相結合的方法，研究建立其非線性動力學模型。

1 系統建模

1.1 系統組成

空氣舵執行機構包括伺服系統和空氣舵機構兩個單元，一般由不同的單位按照控制系統提出的指標設計生產［14］。本文討論的對象是舵機構機械部分，如圖1 所示，包括舵面、舵軸、曲柄連桿等，后續簡稱空氣舵系統。與其連接的邊界是支撐舵軸的軸承和推動舵面轉動的伺服作動器。

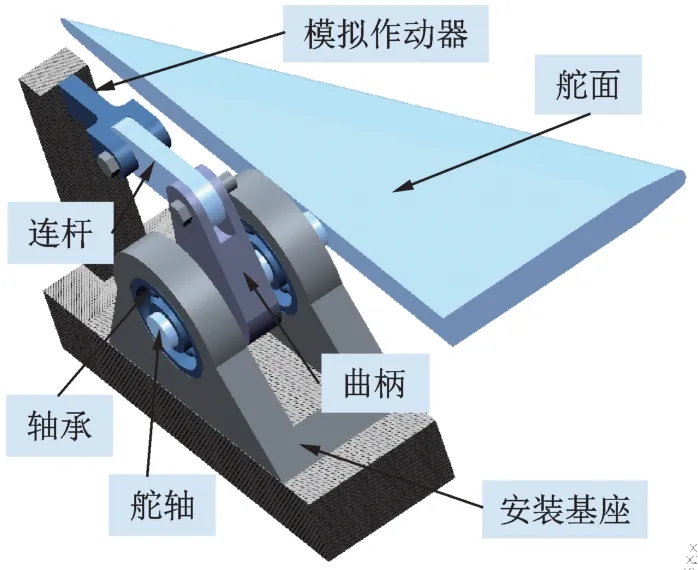
圖1 空氣舵系統Fig.1 The air rudder system

舵面通過舵軸與曲柄連接，舵軸通過軸承安裝于支撐艙段上，作動器推動曲柄使舵軸帶動舵面偏轉，從而產生氣動控制力，通過舵軸和軸承傳遞到飛行器上，控制飛行器姿態和軌跡。

1.2 系統動力學方程

一般航天運載飛行器空氣舵展長等舵面尺寸較小，厚度較大，舵面剛度大，相當于一個剛體，因此舵軸的扭轉剛度和曲柄連桿組件的剛度往往對舵面偏轉過程中系統的剛度起決定性作用。

在舵系統動力學測試時，一般將舵軸的支撐軸承和作動器輸出端固定，在舵面施加激勵，并測量舵面轉角響應，可得到如圖2 所示的空氣舵系統數學模型示意圖。圖2 中，Jr為空氣舵繞舵軸的轉動慣量，K為舵軸與曲柄連桿組件及作動器模擬件串聯后的等效扭轉剛度，C為等效黏性阻尼系數，2e為運動間隙，Tf為舵軸轉動過程的摩擦力矩，Tc為氣動控制力對舵軸的力矩，θr為舵面轉角。雖然從嚴格的機構等效角度看，Jr，K和C會隨著舵面轉角的變化而變化，但是變化量非常小，工程上可近似認定其為常數。

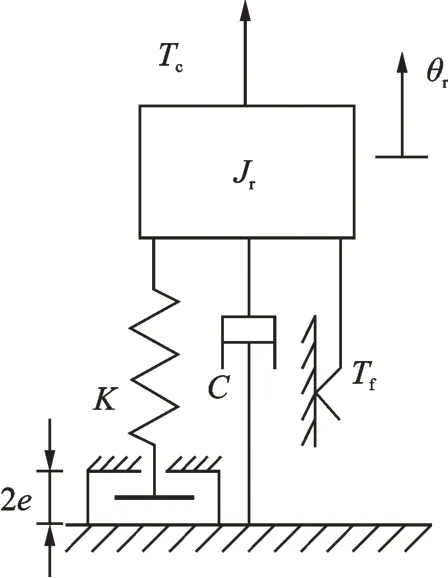
圖2 空氣舵系統數學模型示意圖Fig.2 Mathematical schematic of the air rudder system

根據圖2，空氣舵的動力學方程為：

式中Tk為考慮間隙的彈性恢復力矩，其表達式為：

從已有研究結果看，摩擦力矩Tf一般采用Coulomb 摩擦模型和Stribeck 摩擦模型獲得。如果采用Coulomb 摩擦模型，則：

式中Mf為Coulomb 摩擦力矩。

如果采用Stribeck 摩擦模型，則：

式中Mf為靜摩擦力矩；k1，k3為動摩擦力矩曲線方程系數，具體形式如下：

式中vm為動摩擦力矩最小時的舵面角速度；k0為最小動摩擦力矩與靜摩擦力矩Mf之比，當k0=1時，Stribeck 摩擦模型退化為Coulomb 摩擦模型。

顯然，無論采用哪種摩擦模型，這都是一個非線性系統，其傳遞函數不能簡單地表示成線性有理分式的形式，通過識別分子分母多項式系數的形式完成傳遞函數參數的確定。因此，需要識別式（1）中所有的物理參數。工程實際中，一般空氣舵轉動慣量Jr是可以測量的，式（1）中獨立的未知參數有4 個（即采用Coulomb 摩擦模型時的K，C，Mf，e）或6 個（即采用Stribeck 摩擦模型時的K，C，Mf，e，k0，vm），因此是一個四參數或六參數模型。

1.3 幅頻響應求解

文獻［10-11］中提出過各種參數識別方法，由于在工程中測量系統的頻響是非常成熟和方便的，因此本文將討論基于頻響測試的舵系統非線性參數識別方法。與文獻［11］的常位移測試和常速度測試不同，本文采用的是傳統的常力測試。

參考圖2，頻響測量時，由激振力取代氣動控制力測量舵面的響應。為了識別系統參數，需要首先得到頻響函數表達式。

采用諧波平衡法對式（1）進行求解。由于飛控系統設計關注頻段只包含主共振，因此，可以忽略高次諧波，僅保留一次諧波項。設在如下正弦激勵下：

舵面響應為：

式中T0和θ0分別為激勵力矩和舵面轉角的幅值；ω為激勵頻率；h為響應與激勵的相位差。

1.3.1 四參數模型

四參數模型采用Coulomb 摩擦模型。將式（2），（3），（6）和（7）代入式（1）后取出一次諧波項的系數，得到兩個諧波平衡方程：

式中φ=arcsin(e/θ0)。

通過式（8）和（9）消去相位差，得到舵系統四參數模型幅頻函數方程：

由于φ=arcsin(e/θ0)，所以式（10）是一個超越方程，無法求得幅頻函數的精確顯式解析表達式。

觀察式（10），如果令：

為含間隙影響的等效剛度，則可由式（10）求得如下幅頻響應函數：

由式（12）可知，與線性單自由度系統類似，幅頻函數在ω=附近達到極值。

1.3.2 六參數模型

六參數模型采用Stribeck 摩擦模型。將式（2），（4），（6）和（7）代入式（1）后取出一次諧波項的系數，得到兩個諧波平衡方程：

通過式（13）和（14）消去相位差，得到舵系統六參數模型幅頻函數方程：

2 試驗及舵系統參數識別

2.1 試驗情況

對該飛行器實際使用的空氣舵系統開展頻響測量試驗，如圖3 所示。激振點設置在空氣舵根弦的最前端，以獲取較大的扭矩。通過根弦上的兩個加速度傳感器獲取舵面轉角響應。

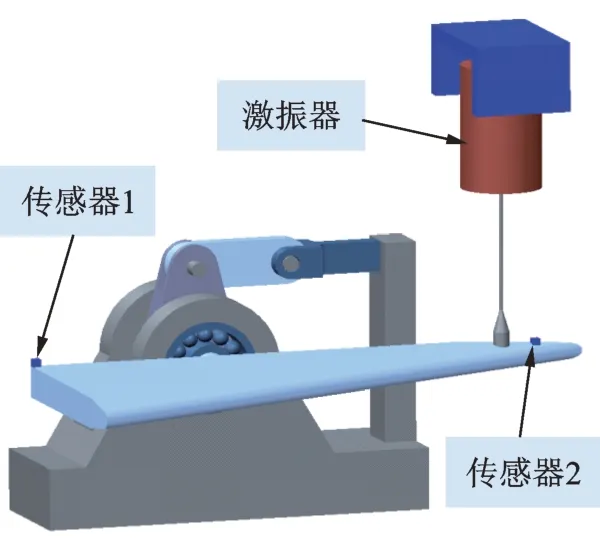
圖3 空氣舵系統頻響試驗Fig.3 FRF test setup of the rudder system

測試時，激振器向舵面施加幅值為常數的正弦掃描激勵，激振力矩與激振力關系按下式計算：

式中l為激振點到舵軸中心的距離。

同時采集加速度傳感器輸出，并由下式計算得到舵面轉角加速度，通過頻域分析獲得頻響曲線：

式中A1和A2為加速度傳感器測量值；L為兩個加速度傳感器間的距離。

試驗測量了等效扭轉力矩幅值分別為70 N·m（A 組）和60 N·m（B 組）的兩組數據，結果如圖4 所示。圖4 中λ為采用控制系統關注頻帶上限頻率歸一化后的無量綱頻率比。頻率歸一化對應的轉動慣量Jr=63062.8 N ?m。

圖4 某飛行器空氣舵系統頻響試驗數據Fig.4 FRF test data of the rudder system of a launch vehicle

由圖4 可見，隨著激振力矩幅值的增加，主共振頻率和共振峰峰值都有明顯提高，這是典型的非線性系統動力學特征。

2.2 參數識別

工程實際中，頻響測試的激振力矩幅值T0(ω)和響應幅值θ0(ω)是可測得的。根據式（10）和（15）隱函數形式幅頻函數，采用MATLAB 非線性最小二乘工具nlinfit 函數擬合試驗數據即可完成物理參數的識別。該工具函數使用高斯-牛頓算法，計算時間短、效率高，但比較依賴初值的選取。因此，可以用兩組頻響測試峰值點處的頻率ω0，力矩幅值T0(ω0)，響應幅值θ0(ω0)等信息，根據式（12）對K，C，Mf，e的值進行初步估計，作為使用nlinfit 函數的初值。

分別對A 組、B 組和（A+B）組測試數據進行擬合，結果如表1 和2，圖5 和6 所示。其中，（A+B）組識別工況是指將A 組和B 組測試數據聯合起來作為nlinfit 函數的輸入數據進行參數辨識，用以考察是否存在一個擬合結果可以同時兼顧A 組和B 組測試數據。

表1 四參數模型識別結果（頻率歸一化后）Tab.1 Identified values with the four-parameter model（with frequency normalization）

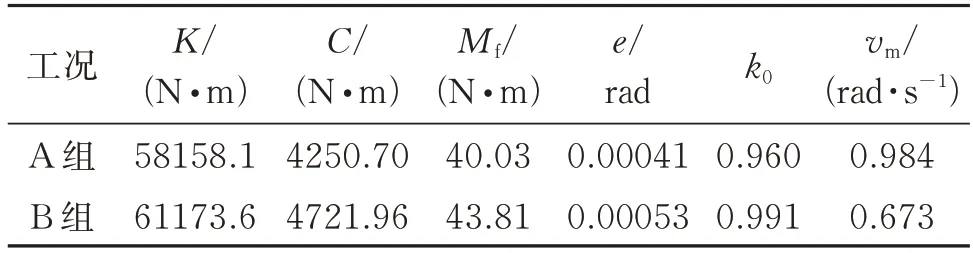
表2 六參數模型識別結果（頻率歸一化后）Tab.2 Identified values with the six-parameter model（with frequency normalization）

圖5 四參數模型擬合結果Fig.5 Curve fittings of the test data with the four-parameter model

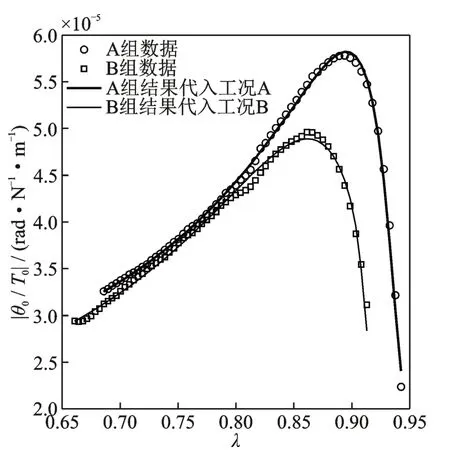
圖6 六參數模型擬合結果Fig.6 Curve fittings of the test data with the six-parameter model

從識別結果可見：

（1）無論采用四參數模型（Coulomb 摩擦模型）還是六參數模型（Stribeck 摩擦模型），采用單一工況數據時，都可以較好地擬合試驗數據，但是識別的Stribeck 摩擦模型參數k0接近1，基本退化至Coulomb 摩擦模型。

（2）單獨采用A 組或B 組測試數據進行擬合時，擬合結果和試驗結果均吻合較好，但是兩組數據識別的結果有一定差異。出現此現象有兩種可能：一是模型不可靠，將每種工況識別的參數代入模型只是對真實舵系統在該工況的一種近似“等效”；二是這個非線性擬合問題的解不唯一，兩組數據識別得到的兩組模型參數結果至少有一組是“虛假”的。如果是后者，那么同時采用兩組測試數據，即（A+B）組工況，識別的模型參數結果應也適用于A 組和B組試驗數據。然而，從圖5 看，情況恰恰相反，（A+B）組識別結果并不能分別很好地擬合A 組和B 組數據。

綜上可知，四參數模型和六參數模型都只能在單一激勵工況近似“等效”地描述實際系統幅頻傳遞特性，由一個工況測試結果識別出的系統參數并不能用來預示其余工況的動力學特性。因此，這兩個模型都不夠可靠。

3 五參數模型及識別結果

第1 節和第2 節所討論的兩個模型由于可靠性不足，無法用于飛控系統的設計與分析。本節將對其進行改進，提高模型可靠性。考慮到對于該空氣舵，Stribeck 摩擦模型相對于Coulomb 摩擦模型并無明顯優勢，因此在原四參數Coulomb 摩擦模型基礎上進行改進。

參考圖3，當激振器激勵舵面時，對舵軸除了產生扭矩Tc(t)，還對舵軸支撐軸承運動副有一個正壓力F(t)。那么根據接觸面Coulomb 摩擦的產生機理，由這個隨時間變化的激振力產生的摩擦力矩大小也與其成正比，即與Tc(t)成正比。因此，可在式（3）基礎上，將摩擦力矩Tf進行細化，描述如下：

式中Mf為摩擦力矩的常值項；|μ?Tc(t)|為比例項，引入的新參數μ為摩擦系數。此時，式（1）描述的系統模型中獨立的未知參數有5 個（即K，C，Mf，μ，e），變成一個五參數模型。

采用諧波平衡法，忽略高次諧波，將式（2），（18），（6）和（7）代入式（1）后取出一次諧波項的系數，得到兩個諧波平衡方程：

考察式（19）和（20），由于相位差h不僅在三角函數中存在，在三角函數外也存在，無法類似四參數模型通過兩個諧波平衡方程消去相位差得到幅頻函數方程。因此，五參數模型參數識別僅采用幅頻測試數據是不夠的，需要同時采用幅頻和相頻測試數據。

在四參數模型參數識別基礎上，應用五參數模型，通過非線性擬合法分別對A 組、B 組和（A+B）組測試數據進行擬合，結果如表3 和圖7 所示。

表3 五參數模型識別結果（頻率歸一化后）Tab.3 Identified values with the five-parameter model（with frequency normalization）

圖7 五參數模型擬合結果Fig.7 Curve fittings of the test data with the five-parameter model

可見，采用不同測試數據識別獲得的5 個參數一致性較好，說明五參數模型可以更可靠地描述該空氣舵系統動力學特性。

五參數模型與四參數模型的差別在于摩擦模型。無論何種摩擦模型，其作用都是耗能，在幅頻響應分析中可采用能量等效的原則，將其簡化為線性黏性阻尼［15］。Coulomb 摩擦模型或改進摩擦模型式（18）中的常值項等效阻尼系數為：

它不是常值，反比于振動頻率及振幅。

式（18）中的比例項等效阻尼系數為：

它也不是常值，反比于振動頻率及振幅，正比于激振力幅值，并與相位差h相關。

根據式（21）和（22），五參數模型總的等效阻尼系數為：

四參數模型總的等效阻尼系數為：

代入表1 和3 中的參數，以及圖4 中的試驗數據，得到A 組和B 組工況兩種模型總等效阻尼系數對比情況，如圖8 所示。

圖8 兩種模型總等效阻尼系數的對比Fig.8 Comparison of the total equivalent damping coefficients between the two models

單獨看A 組工況或B 組工況，四參數模型識別結果得到的總等效阻尼系數大小和隨頻率變化特點均與五參數模型接近，特別是在共振峰附近，二者幾乎一致，但四參數模型A 組和B 組工況識別的系統參數差異較大，五參數模型兩個工況基本保持一致，說明四參數模型及其參數辨識結果只能在單一激勵工況近似“等效”為五參數模型。

值得指出的是，火箭等飛行器在大空區域、寬速域飛行過程中，飛行動壓、攻角和舵偏角均實時變化，舵面負載隨之變化。摩擦系數μ的引入，可以反映舵系統摩擦力矩在飛行中的變化情況，適用性更強。

此外，對比表1，2 和3，五參數模型剛度和間隙參數的識別結果相對四參數模型較小。參考式（11），間隙正誤差增加可以一定程度抵消剛度正誤差，所以僅從幅頻響應角度，表1，2 和3 的剛度和間隙參數都是滿足擬合要求的。但是五參數模型參數識別中使用了相頻信息，因此表3 的識別結果更可靠。

4 結論

本文以某航天飛行器空氣舵系統為對象，考慮運動副間隙和摩擦，采用理論與試驗相結合的方法，研究了系統非線性動力學建模問題，提出一種基于改進Coulomb 摩擦模型的五參數模型。相比于基于Coulomb 摩擦模型的四參數模型和基于Stribeck 摩擦模型的六參數模型，五參數動力學模型擬合不同工況測試數據獲得的系統參數一致性更好，四參數模型及其參數辨識結果只能在單一激勵工況近似“等效”五參數模型。因此，五參數模型更可靠，可用于預測其余工況舵系統非線性動力學特性。

實際飛行中，存在舵面激勵力矩幅值上百牛米的工況。五參數模型能計入激勵力矩變化對摩擦力矩的影響，適用性更強。