計(jì)入結(jié)構(gòu)柔性的風(fēng)電齒輪箱行星輪系動(dòng)力學(xué)特性研究

譚建軍，李 浩，冉 峯，朱才朝，宋朝省，李祖鋒

（1.重慶大學(xué)機(jī)械傳動(dòng)國家重點(diǎn)實(shí)驗(yàn)室，重慶 400044；2.重慶工商大學(xué)智能制造服務(wù)國際科技合作基地，重慶 400067）

引言

在“十四五”期間，中國風(fēng)電補(bǔ)貼國家政策將全面取消，對風(fēng)電機(jī)組度電成本提出了嚴(yán)苛要求，而發(fā)展10 MW 及以上超大功率風(fēng)電機(jī)組是降低度電成本的有效措施之一［1］。具有多行星輪功率分流的風(fēng)電齒輪箱被廣泛應(yīng)用于風(fēng)電機(jī)組中傳遞兆瓦級(jí)功率，是極為重要的傳動(dòng)裝置。為了滿足更大功率的傳遞需求，風(fēng)電齒輪箱行星輪系內(nèi)齒圈和行星架等構(gòu)件尺寸將會(huì)設(shè)計(jì)得更大，行星輪數(shù)量也將增多，容易在隨機(jī)氣動(dòng)轉(zhuǎn)矩作用下產(chǎn)生過大的系統(tǒng)振動(dòng)噪聲和動(dòng)載荷，增大疲勞失效風(fēng)險(xiǎn)。因此，開展計(jì)入結(jié)構(gòu)柔性的風(fēng)電齒輪箱行星輪系動(dòng)力學(xué)特性研究具有重要意義。

國內(nèi)外學(xué)者圍繞行星輪系動(dòng)力學(xué)建模、固有特性和動(dòng)態(tài)響應(yīng)等開展了深入研究，取得了諸多有益的研究成果。Lin 等［2］利用行星輪系動(dòng)力學(xué)模型分析了軸承支撐剛度、齒輪副嚙合剛度等設(shè)計(jì)參數(shù)對系統(tǒng)固有頻率與模態(tài)動(dòng)能的影響，發(fā)現(xiàn)了模態(tài)躍遷現(xiàn)象。Eritenel 等［3］分析了行星輪系自由振動(dòng)模態(tài)，將行星輪系振動(dòng)模態(tài)歸納為三類振動(dòng)模式，即中心構(gòu)件扭轉(zhuǎn)、中心構(gòu)件平移和行星輪振動(dòng)模式。Guo等［4-5］考慮時(shí)變嚙合剛度、非線性齒面接觸和軸承游隙等時(shí)變參數(shù)激勵(lì)，分析了行星輪系非線性振動(dòng)特性。Zhai 等［6］考慮時(shí)變行星架裝配誤差，建立了多級(jí)行星輪系動(dòng)力學(xué)模型，分析了行星輪系動(dòng)態(tài)嚙合力。?ztürk 等［7］以彈性力學(xué)為基礎(chǔ)建立了行星輪系純扭轉(zhuǎn)動(dòng)力學(xué)模型，研究了輪齒修形對行星輪系振動(dòng)特性的影響。為了提高行星輪系動(dòng)力學(xué)模型計(jì)算精度，Parker 等［8］將內(nèi)齒圈視為彈性連續(xù)體，建立行星輪系彈性-集中參數(shù)混合動(dòng)力學(xué)模型，分析了行星輪非均布對系統(tǒng)固有特性的影響，在常見的三類振動(dòng)模式［3］基礎(chǔ)之上，發(fā)現(xiàn)了內(nèi)齒圈的彎曲振動(dòng)模式。Fan 等［9］、Guan 等［10］采用殼理論 和Timoshenko 梁理論計(jì)算內(nèi)齒圈結(jié)構(gòu)柔性，建立行星輪系殼/梁單元-集中參數(shù)混合動(dòng)力學(xué)模型，分析了內(nèi)齒圈動(dòng)態(tài)變形和系統(tǒng)固有特性。Kahraman 等［11］采用有限元法建立了行星輪系準(zhǔn)靜態(tài)分析模型，分析了內(nèi)齒圈柔性對構(gòu)件動(dòng)應(yīng)力和變形的影響。張俊等［12］將連續(xù)體柔性內(nèi)齒圈離散為多段等效虛擬彈簧連接的剛性內(nèi)齒圈段，研究了內(nèi)齒圈柔性對系統(tǒng)固有特性的影響。許華超等［13］采用平面梁單元建立彈性邊界柔性直齒內(nèi)齒圈的振動(dòng)分析模型，分析了組合激勵(lì)下系統(tǒng)固有特性。魏靜等［14］采用軸系單元將內(nèi)齒圈和行星架進(jìn)行離散化建模，研究了內(nèi)齒圈和行星架結(jié)構(gòu)柔性對多級(jí)行星輪系動(dòng)態(tài)嚙合力的影響。為了考慮復(fù)雜結(jié)構(gòu)幾何特征，Abousleiman 等［15］、Portron 等［16］考慮內(nèi)齒圈柔性，采用有限元法建立了行星輪系有限元-集中參數(shù)混合動(dòng)力學(xué)模型，分析了系統(tǒng)振動(dòng)特性。Betta?eb 等［17］、Guilbert 等［18］將模態(tài)綜合法引入到定軸齒輪動(dòng)力學(xué)建模中，有效提高了建模精度，并降低了系統(tǒng)自由度。隨后，許華超等［19］采用有限元-集中參數(shù)混合方法建立計(jì)入傳動(dòng)軸和機(jī)匣結(jié)構(gòu)柔性的直升機(jī)主減速器混合動(dòng)力學(xué)模型，研究了機(jī)匣結(jié)構(gòu)對系統(tǒng)振動(dòng)特性的影響。

目前，行星輪系動(dòng)力學(xué)建模方法可以大致劃分為集中參數(shù)模型［2-7，12］、混合模型［8-10，13-19］和有限元模型［11］。集中參數(shù)模型側(cè)重于對系統(tǒng)固有特性、激勵(lì)機(jī)理及動(dòng)態(tài)載荷分配等進(jìn)行初步分析，在建模時(shí)常將齒輪、軸和軸承簡化為一體，以簡單徑向、彎曲和扭轉(zhuǎn)剛度代替彈性軸的復(fù)雜受載狀況。此類模型未計(jì)入內(nèi)齒圈、行星架和箱體等構(gòu)件的彈性變形，整體計(jì)算精度不高。混合模型包括梁/殼單元-集中參數(shù)混合模型和有限元-集中參數(shù)混合模型，由于此類建模方法在集中參數(shù)模型的基礎(chǔ)之上計(jì)入了內(nèi)齒圈、行星架和傳動(dòng)軸等構(gòu)件的彈性變形，整體計(jì)算精度得到提高。相比于梁/殼單元-集中參數(shù)混合模型，有限元-集中參數(shù)混合模型可以考慮復(fù)雜的結(jié)構(gòu)幾何特征，適用性更好，但多用于恒定轉(zhuǎn)速下的振動(dòng)分析，少有文獻(xiàn)關(guān)注計(jì)入內(nèi)齒圈結(jié)構(gòu)柔性的行星輪系變速變載動(dòng)力學(xué)建模。此外，集中參數(shù)模型和混合模型常將齒輪副多輪齒嚙合簡化為等效單點(diǎn)嚙合，以簡單的綜合嚙合剛度代替復(fù)雜的多輪齒嚙合過程，造成在求解輪齒動(dòng)載荷時(shí)精度不高。有限元模型可以考慮復(fù)雜結(jié)構(gòu)幾何特征，并能較好地模擬輪齒接觸狀態(tài)，全面反映行星輪系各構(gòu)件受載狀況，但此類模型建模過程復(fù)雜、計(jì)算量龐大、系統(tǒng)級(jí)建模分析困難，一般不適用于動(dòng)態(tài)設(shè)計(jì)場合。

綜上所述，為了提高變速變載工況下風(fēng)電齒輪箱行星輪系動(dòng)力學(xué)性能的預(yù)測精度，針對常規(guī)梁/殼單元無法考慮復(fù)雜構(gòu)件幾何特征、計(jì)算精度低和大規(guī)模有限元計(jì)算量大、系統(tǒng)級(jí)建模分析困難的問題，基于有限元-集中參數(shù)混合模型，提出一種計(jì)入結(jié)構(gòu)柔性的行星輪系變速動(dòng)力學(xué)建模方法。以某型5 MW 級(jí)風(fēng)電齒輪箱低速級(jí)行星輪系為研究對象，采用有限元縮聚理論對內(nèi)齒圈和行星架進(jìn)行建模，并將齒輪嚙合副常規(guī)等效單點(diǎn)嚙合細(xì)化至多對輪齒嚙合，建立能夠反映復(fù)雜構(gòu)件幾何特征、輪齒動(dòng)載荷且適用于變速運(yùn)行的行星輪系動(dòng)力學(xué)模型，為風(fēng)電齒輪箱行星輪系動(dòng)態(tài)設(shè)計(jì)提供理論基礎(chǔ)。

1 行星輪系動(dòng)力學(xué)建模

1.1 子結(jié)構(gòu)縮聚單元

由于實(shí)際工程結(jié)構(gòu)往往較為復(fù)雜，整體結(jié)構(gòu)有限元模型節(jié)點(diǎn)自由度數(shù)量龐大，造成計(jì)算效率低、收斂慢等問題，因此常采用子結(jié)構(gòu)縮聚方法消除“整體單元”中除需要保留節(jié)點(diǎn)以外的所有節(jié)點(diǎn)自由度，將子結(jié)構(gòu)系統(tǒng)矩陣規(guī)模縮減至可接受的維度。

建立如圖1 所示的行星架（c）和內(nèi)齒圈（r）有限元模型，根據(jù)其結(jié)構(gòu)特征，在其連接位置、軸承支撐和內(nèi)齒圈輪齒處設(shè)置縮聚點(diǎn)，包括行星架的驅(qū)動(dòng)力矩（縮聚點(diǎn)1）、軸承支撐（縮聚點(diǎn)2 和3）和銷軸（縮聚點(diǎn)4～8）；內(nèi)齒圈的輪齒（縮聚點(diǎn)1～93）、箱體連接（縮聚點(diǎn)94 和95）和螺栓連接（縮聚點(diǎn)96～120）。定義如圖2 所示的O-XYZ為原點(diǎn)固定在內(nèi)齒圈中心的絕對坐標(biāo)系；orj-xrjyrjzrj為原點(diǎn)固定在內(nèi)齒圈輪齒縮聚點(diǎn)和螺栓連接縮聚點(diǎn)的絕對坐標(biāo)系，且與O-XYZ平行；oc-xcyczc為原點(diǎn)固定在行星架中心并隨其轉(zhuǎn)動(dòng)的隨動(dòng)坐標(biāo)系；ocpi-xcpiycpizcpi為原點(diǎn)固定在銷軸縮聚點(diǎn)并隨行星架轉(zhuǎn)動(dòng)的隨動(dòng)坐標(biāo)系，且與oc-xcyczc平行。此外，內(nèi)齒圈縮聚點(diǎn)94 和95 參照O-XYZ；行星架縮聚點(diǎn)1～3 參照oc-xcyczc。Rc為太陽輪到行星輪的中心距離，?pi為行星輪i的位置角。

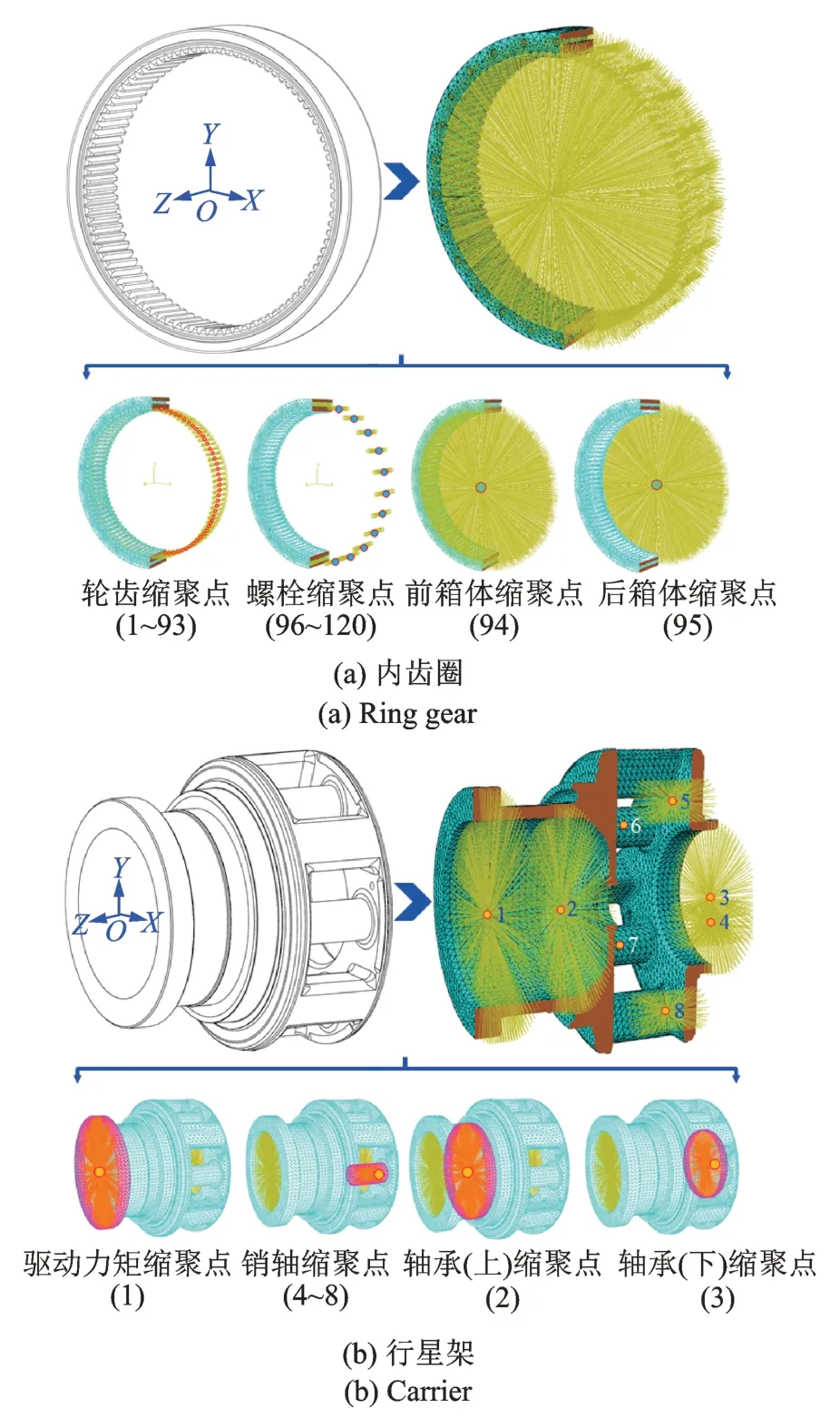
圖1 有限元縮聚模型Fig.1 Finite element condensation model

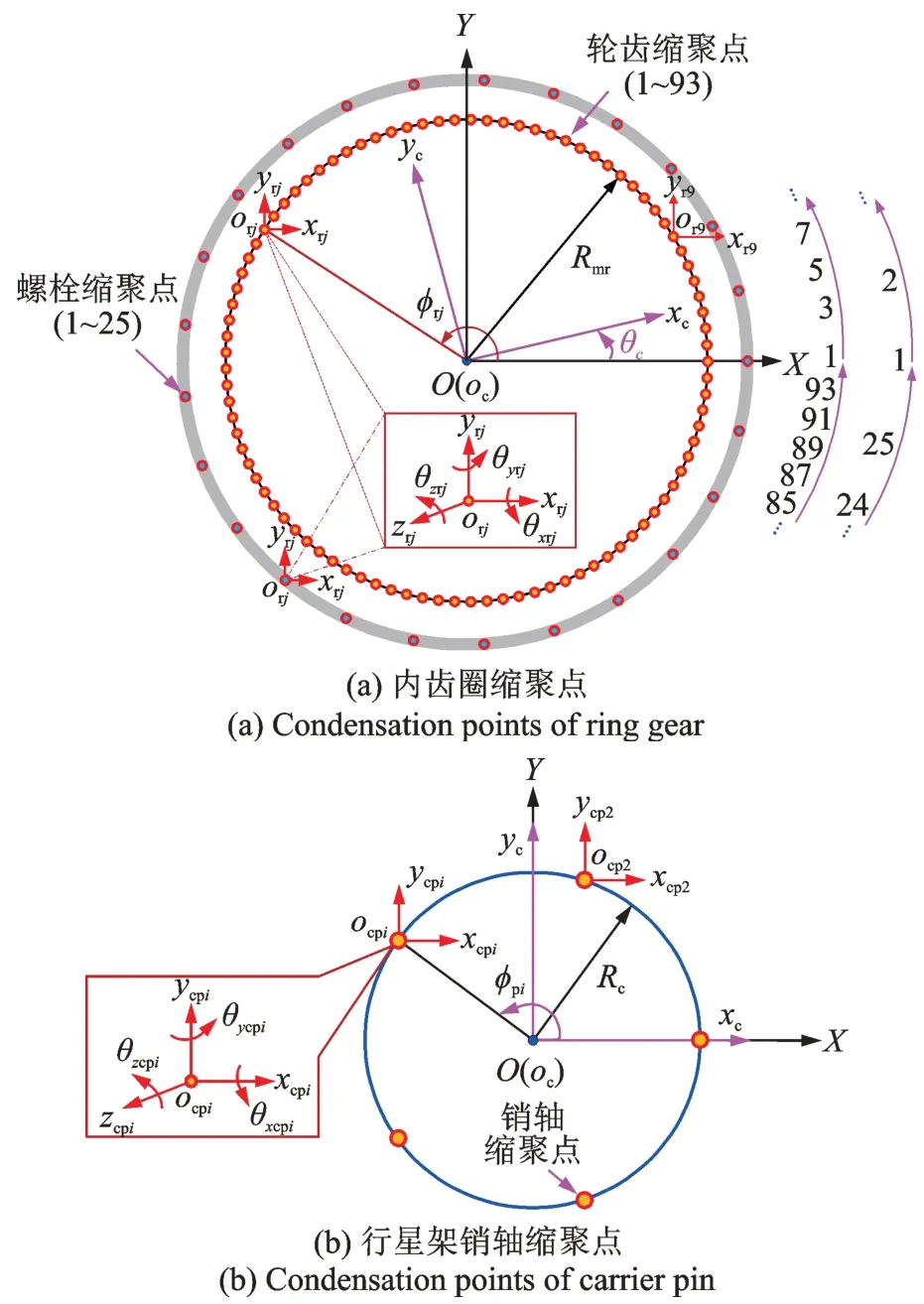
圖2 縮聚點(diǎn)坐標(biāo)系定義Fig.2 Definition of coordinate systems of condensation points

內(nèi)齒圈輪齒縮聚點(diǎn)設(shè)置在每個(gè)輪齒節(jié)圓且位于齒寬中心位置處，則根據(jù)角度可以計(jì)算出任意內(nèi)齒圈輪齒節(jié)點(diǎn)在O-XYZ中的坐標(biāo)如下式所示：

式中Rmr為內(nèi)齒圈節(jié)圓半徑；?rj為內(nèi)齒圈輪齒節(jié)點(diǎn)j的位置角。

同理可得螺栓連接縮聚點(diǎn)坐標(biāo)，不再詳述。

通過柔性多點(diǎn)約束（MPC）［20］將縮聚點(diǎn)與對應(yīng)的界面節(jié)點(diǎn)進(jìn)行連接，采用固定界面模態(tài)綜合法對行星架和內(nèi)齒圈進(jìn)行子結(jié)構(gòu)縮聚，可得縮聚后構(gòu)件χ（χ=r，c）在自身參考坐標(biāo)系下的位移向量為：

可得縮聚后行星架和內(nèi)齒圈的自由振動(dòng)方程為：

1.2 嚙合與支撐單元

采用如圖3 所示的廣義坐標(biāo)系對太陽輪和行星輪進(jìn)行建模，包括太陽輪隨動(dòng)坐標(biāo)系os-xsyszs和行星輪隨動(dòng)坐標(biāo)系opi-xpiypizpi，xpi和ypi分別為行星輪徑向和切向方向。行星輪中心與對應(yīng)的行星架銷軸縮聚點(diǎn)重合，行星架縮聚點(diǎn)轉(zhuǎn)動(dòng)自由度（υ取值參考圖1（b））參照O-XYZ，其余自由度參照oc-xcyczc和ocpi-xcpiycpizcpi（見1.1 節(jié)）。Rbs，Rbp和Rbr分別為太陽輪、行星輪和內(nèi)齒圈的基圓半徑。圖4 所示為行星輪系嚙合副中輪齒動(dòng)態(tài)嚙合點(diǎn)Mc在嚙合平面上的位置。

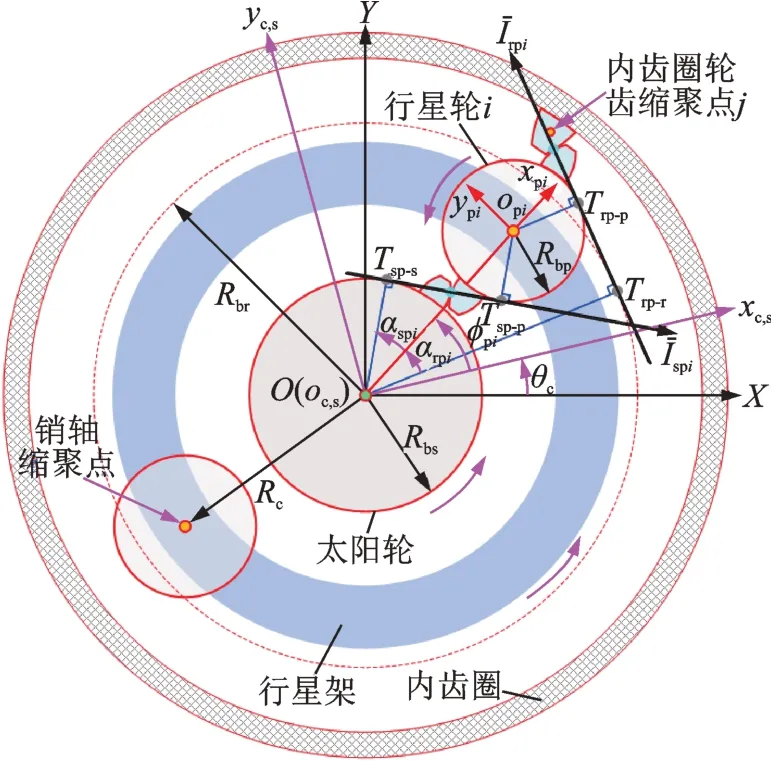
圖3 行星輪系嚙合副Fig.3 Meshing gear pairs in the planetary gear train

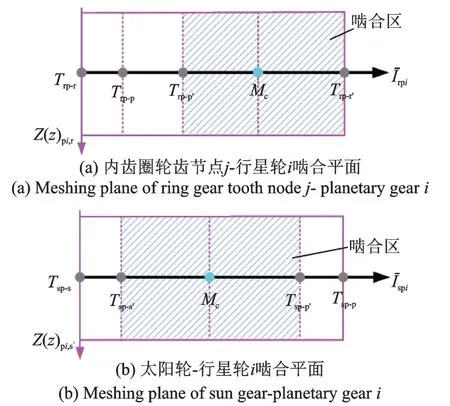
圖4 行星輪系嚙合平面Fig.4 Meshing plane of the planetary gear train

1.2.1 嚙合單元

基于δspi(Mc)和(Mc)，可得太陽輪-行星輪i嚙合副、內(nèi)齒圈輪齒節(jié)點(diǎn)j-行星輪i嚙合副在嚙合點(diǎn)Mc處時(shí)，各構(gòu)件6 個(gè)自由度廣義位移向嚙合線方向轉(zhuǎn)化的投影矢量分別如下式所示［22］：

然而，在文獻(xiàn)［2-14，17-19］中太陽輪-行星輪嚙合副和內(nèi)齒圈-行星輪嚙合副常采用等效綜合嚙合剛度將嚙合副中多輪齒嚙合過程簡化為等效單點(diǎn)嚙合，其嚙合剛度矩陣Ksp(Mc)和Krp(Mc)分別如下式所示：

式中Np為行星輪數(shù)量；Λ為定位矩陣，即將嚙合剛度矩陣擴(kuò)展至整個(gè)系統(tǒng)矩陣；Kspi和Krpi分別為太陽輪-行星輪i嚙合副、內(nèi)齒圈-行星輪i嚙合副的綜合嚙合剛度；Vspi和Vrpi為對應(yīng)的嚙合向量，并未細(xì)化至每對嚙合輪齒。

嚙合阻尼矩陣Csp(Mc)和Crp(Mc)的形式分別與式（7）和式（8）相同，其中嚙合阻尼采用經(jīng)驗(yàn)公式計(jì)算，見文獻(xiàn)［23］。

基于式（7）和（8），按照“化整為零”的思想，將齒輪副綜合嚙合剛度按照其重合度等效分解到每對嚙合輪齒上，同時(shí)為了模擬每對嚙合輪齒從嚙入到嚙出的狀態(tài)變化，引入輪齒嚙合判斷系數(shù)和可得：

式中Nr為內(nèi)齒圈齒數(shù)；為太陽輪-行星輪i嚙合副中參與嚙合的第l對齒嚙合剛度；為第j個(gè)內(nèi)齒圈輪齒節(jié)點(diǎn)在內(nèi)齒圈-行星輪i嚙合副中對應(yīng)參與嚙合的第l對齒嚙合剛度；ceil(?)為朝正無窮大方向取整；ξ為重合度；為太陽輪-行星輪i嚙合副中參與嚙合的第l對輪齒嚙合向量；為內(nèi)齒圈輪齒節(jié)點(diǎn)j-行星輪i嚙合副中參與嚙合的輪齒嚙合向量。

式中l(wèi)spi∈[1，ceil(ξspi)]，lrpi∈[1，ceil(ξrpi)]。

在嚙合區(qū)內(nèi)（見圖4），嚙合點(diǎn)從嚙入到嚙出剛好經(jīng)歷一個(gè)單對齒嚙合剛度變化周期，可得：

式中Tspi和Trpi為單對齒嚙合剛度變化周期；pbt為基圓節(jié)距。

1.2.2 支撐單元

行星架銷軸縮聚點(diǎn)與行星輪通過軸承支撐單元耦合，但銷軸縮聚點(diǎn)的參考坐標(biāo)系與行星輪節(jié)點(diǎn)不一致，需要采用旋轉(zhuǎn)矩陣Tcp［26］將銷軸縮聚點(diǎn)的廣義位移向量轉(zhuǎn)換至坐標(biāo)系opi-xpiypizpi：

基于式（15），可得銷軸縮聚點(diǎn)與對應(yīng)行星輪節(jié)點(diǎn)的耦合剛度矩陣Kcp為：

1.3 軸段單元

結(jié)合如圖5 所示的太陽輪軸結(jié)構(gòu)特征，采用計(jì)入剪切變形影響的修正Euler-Bernouli 梁單元［27］，建立軸段梁單元?jiǎng)恿W(xué)方程。其中，第J個(gè)梁單元包括2 個(gè)節(jié)點(diǎn)，每個(gè)節(jié)點(diǎn)考慮6 個(gè)自由度，定義在自身參考坐標(biāo)下的廣義位移向量為：

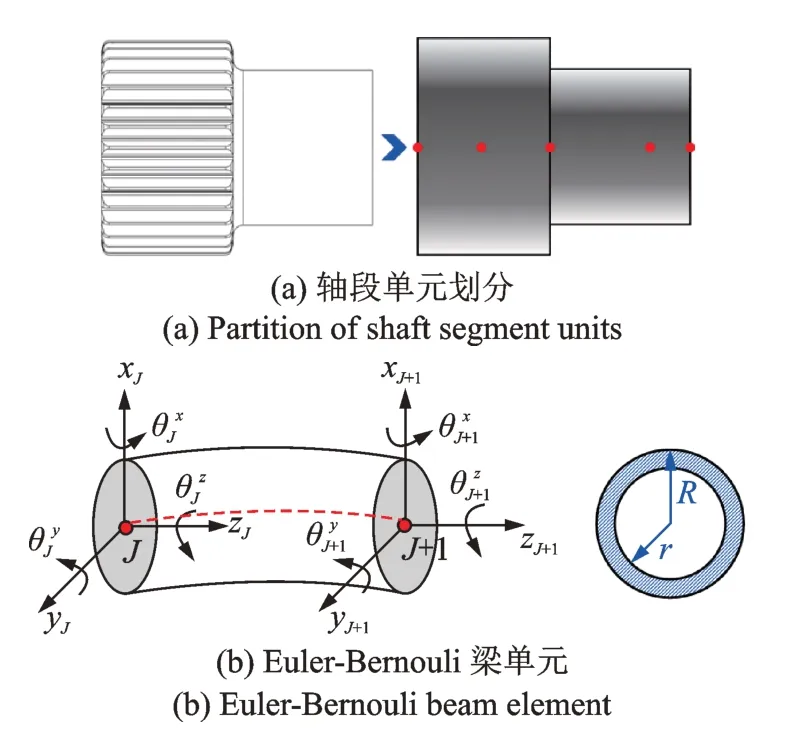
圖5 太陽輪軸段單元建模Fig.5 Modeling of sun shaft segment

可得第J個(gè)梁單元自由振動(dòng)方程為：

1.4 激振力單元

齒形誤差是齒輪制造加工中產(chǎn)生的典型高頻誤差，在齒輪嚙合過程中表現(xiàn)為周期性位移激勵(lì)，可以通過三坐標(biāo)測量機(jī)等儀器實(shí)測獲取。本文僅考慮單齒切向偏差，其與齒輪嚙頻相關(guān)，將其視作簡諧函數(shù)［23］，可得齒輪副嚙合誤差表達(dá)式為：

此外，結(jié)合式（9）和（10），可得由內(nèi)齒圈虛擬振動(dòng)線位移Rbr產(chǎn)生的激振力矩陣為：

同理，可得由齒輪嚙合誤差產(chǎn)生的誤差激振力矩陣，不再詳述。

1.5 系統(tǒng)耦合模型

根據(jù)如圖6 所示的太陽輪、內(nèi)齒圈、行星架和行星輪節(jié)點(diǎn)自由度及其耦合關(guān)系，定義系統(tǒng)節(jié)點(diǎn)在自身參考坐標(biāo)下的廣義位移向量為：

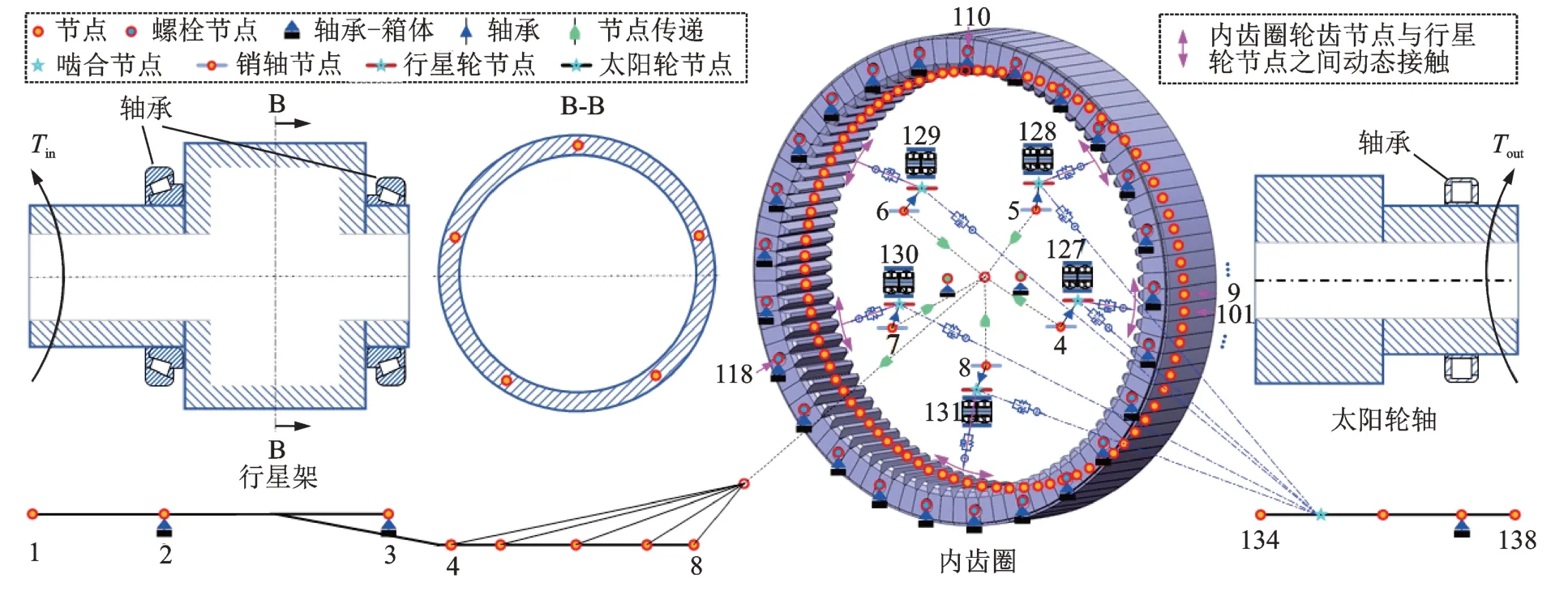
圖6 行星輪系耦合模型Fig.6 Coupling model of the planetary gear train

將太陽輪、內(nèi)齒圈、行星架和行星輪的質(zhì)量矩陣、剛度矩陣與阻尼矩陣按照式（21）所示順序進(jìn)行組裝，建立行星輪系動(dòng)力學(xué)模型：

式中Msys，Ksys和Csys分別為系統(tǒng)質(zhì)量矩陣、剛度矩陣和阻尼矩陣；Fsys為系統(tǒng)激振力矩陣，包括輸入扭矩（Tin）、誤差激勵(lì)、內(nèi)齒圈虛擬振動(dòng)線位移激勵(lì)和負(fù)載（Tout），其中負(fù)載根據(jù)太陽輪轉(zhuǎn)速對轉(zhuǎn)速-轉(zhuǎn)矩運(yùn)行特性曲線進(jìn)行插值得到［29］。

行星輪系動(dòng)力學(xué)模型，共計(jì)138 個(gè)節(jié)點(diǎn)+120 階內(nèi)部節(jié)點(diǎn)保留模態(tài)，948 個(gè)自由度。

由于模型自由度數(shù)量較大，造成行星輪系動(dòng)力學(xué)模型求解困難，本文采用精細(xì)積分法（PIM）［30］求解式（22），計(jì)算各節(jié)點(diǎn)振動(dòng)位移和振動(dòng)速度，步長取為1×10–5。

2 結(jié)果分析與討論

某型5 MW 級(jí)海上風(fēng)電齒輪箱低速級(jí)行星輪系齒輪參數(shù)和軸承支撐剛度分別如表1 和2 所示，時(shí)變嚙合剛度和嚙合誤差如圖7 所示。其中，嚙合剛度和軸承支撐剛度采用ROMAX 軟件在額定工況下計(jì)算得到，齒輪選用5 級(jí)精度。

表1 行星輪系齒輪參數(shù)Tab.1 Gear parameters in the planetary gear train

表2 軸承支撐剛度Tab.2 Bearing supporting stiffness

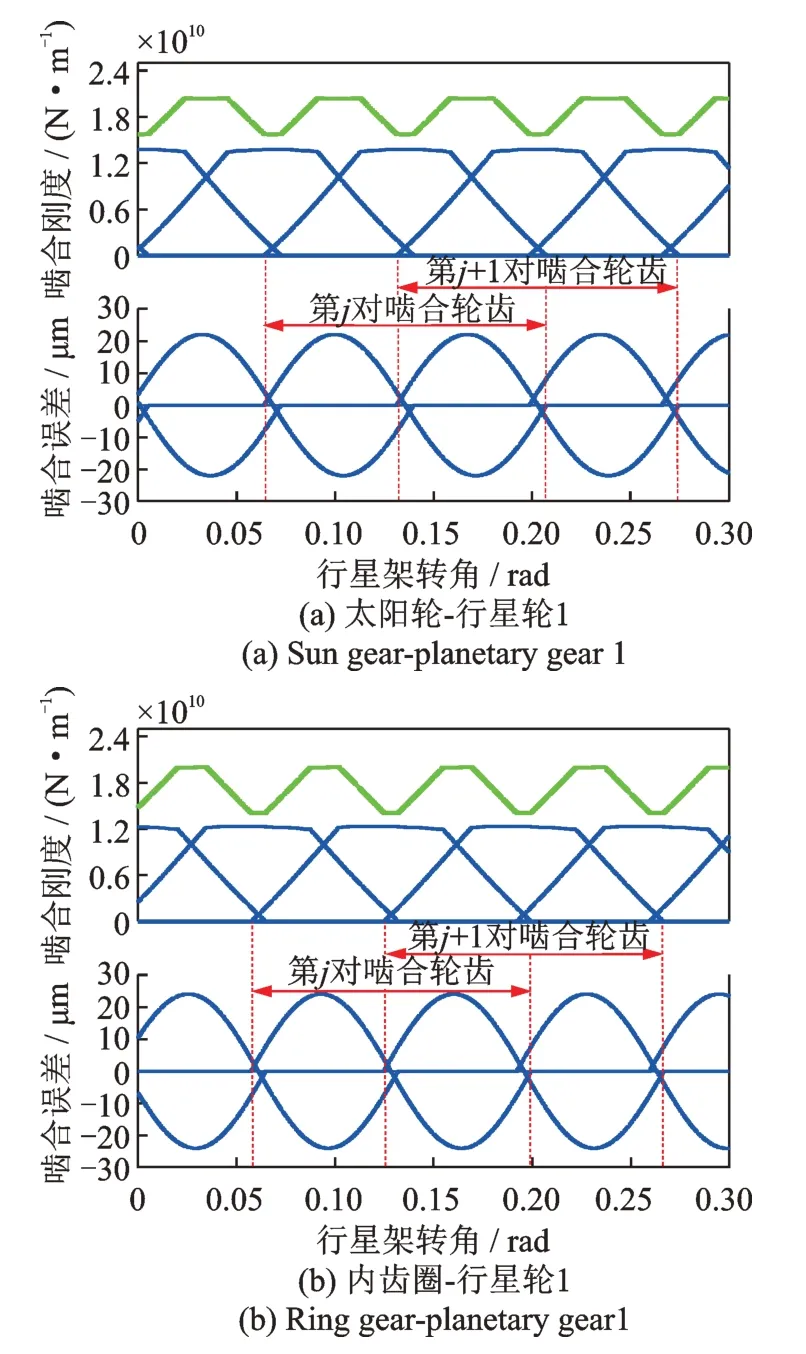
圖7 時(shí)變嚙合剛度和嚙合誤差Fig.7 Time-varying meshing stiffness and meshing error

2.1 模型驗(yàn)證

在額定工況下（Tin=4×106N?m），當(dāng)行星架分別動(dòng)態(tài)旋轉(zhuǎn)至2π/10 rad 和2π/5 rad 時(shí)，行星輪、內(nèi)齒圈和太陽輪的瞬態(tài)受力平衡位置如圖8 所示，其中紅色線表示變形后的狀態(tài)，藍(lán)色線表示原始狀態(tài)。圖9 所示為在行星架3D 有限元模型中，當(dāng)A-A 處縮聚點(diǎn)固定時(shí)，在行星架銷軸縮聚點(diǎn)施加順時(shí)針（正視B-B 平面）切向力后行星架靜態(tài)變形，模擬當(dāng)行星架逆時(shí)針旋轉(zhuǎn)時(shí)銷軸縮聚點(diǎn)變形后的狀態(tài)。

圖8 行星輪系各構(gòu)件瞬態(tài)受力平衡位置Fig.8 Transient forced equilibrium position of each component in the planetary gear train

從圖8 中可知，行星輪切向位置變化與行星架旋轉(zhuǎn)方向（逆時(shí)針旋轉(zhuǎn)）相反，這與圖9 所示的有限元模型銷軸切向變形趨勢較為吻合，其主要原因是由于行星輪主要傳遞周向力矩，造成行星輪沿切向的受力較大。此外，內(nèi)齒圈輪齒節(jié)點(diǎn)的受力平衡位置整體呈“五角星”形狀，且會(huì)隨著行星架逆時(shí)針旋轉(zhuǎn)。這是由于內(nèi)齒圈同時(shí)與5 個(gè)行星輪嚙合，導(dǎo)致內(nèi)齒圈受擠壓變形。太陽輪徑向的受力平衡位置變化很小，其主要原因是由于行星輪徑向?qū)ΨQ布置，同時(shí)由于斜齒輪軸向分力相對于徑向分力較小，內(nèi)齒圈、行星架和太陽輪的軸向受力平衡位置變化較小。

2.2 嚙合副變速表征變量

在恒定輸入扭矩（Tin=4×106N?m）和扭矩突變工 況（Tin=4×106→2×106→4×106N ?m，Tin=4×106→0.2×106→4×106N?m）下，行星架轉(zhuǎn)速變化如圖10 所示，對應(yīng)的恒定輸入扭矩工況下內(nèi)齒圈-行星輪嚙合副變速表征變量（和）如圖11 所示。從圖10 中可知，當(dāng)輸入扭矩恒定時(shí)，初始階段行星架轉(zhuǎn)速逐漸增加，隨后達(dá)到額定轉(zhuǎn)速（輸入轉(zhuǎn)速11.27 r/min）并趨于穩(wěn)定波動(dòng)；當(dāng)輸入扭矩驟減時(shí)，行星架轉(zhuǎn)速隨之降低，而當(dāng)扭矩恢復(fù)時(shí)，其逐漸增速至額定轉(zhuǎn)速，同時(shí)還可以觀察到扭矩跌落幅值越大，行星架轉(zhuǎn)速波動(dòng)也越大。從圖11 中可知，隨著行星架轉(zhuǎn)角增大，內(nèi)齒圈齒數(shù)序號(hào)逐漸增大，表明內(nèi)齒圈輪齒依序參與嚙合；并且由于多行星輪嚙合存在相位差異，造成嚙合副變速表征變量的初始位置沿內(nèi)齒圈均勻分布。此外，嚙合副變速表征變量曲線的兩側(cè)邊緣出現(xiàn)了明顯的周期性“毛刺”，這是由于內(nèi)齒圈-行星輪嚙合副重合度為非整數(shù)時(shí)造成的同時(shí)參與嚙合的齒數(shù)周期性變化。

圖10 行星架轉(zhuǎn)速變化Fig.10 Changes of carrier rotation speed

圖11 內(nèi)齒圈-行星輪嚙合副變速表征變量Fig.11 Characteristic variables for describing the variable speed process of meshing gear pairs of ring gear-planetary gear

為了進(jìn)一步分析內(nèi)齒圈輪齒嚙合狀態(tài)的變化規(guī)律，分別提取了內(nèi)齒圈-行星輪1 嚙合副載荷、內(nèi)齒圈輪齒沿x向的振動(dòng)位移，分別如圖12 和13 所示。從圖12 中可知，隨著行星架轉(zhuǎn)角增加大，內(nèi)齒圈-行星輪1 同時(shí)參與嚙合的齒數(shù)在2 和3 之間周期性波動(dòng)，并且各輪齒動(dòng)載荷先增大后減小，整體變化趨勢與單對齒嚙合剛度相似（如圖7 所示）。從圖13 中可知，隨著行星架轉(zhuǎn)角增加，內(nèi)齒圈輪齒振動(dòng)位移出現(xiàn)明顯的循環(huán)波動(dòng)，間隔相位為2π/5 rad，這是由于內(nèi)齒圈同一輪齒先后與不同行星輪嚙合；當(dāng)行星架轉(zhuǎn)角一定時(shí)，內(nèi)齒圈所有輪齒振動(dòng)位移整體呈原點(diǎn)對稱分布，其主要原因是內(nèi)齒圈輪齒動(dòng)載荷方向（沿嚙合線方向）與對應(yīng)的局部坐標(biāo)系之間的夾角會(huì)隨著行星架轉(zhuǎn)動(dòng)而周期性變化。

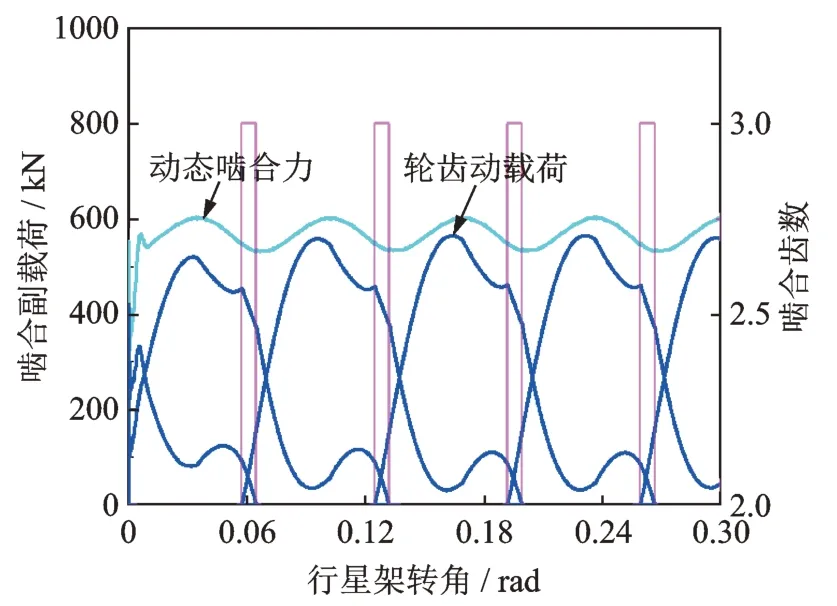
圖12 內(nèi)齒圈-行星輪1 嚙合副載荷Fig.12 Meshing gear pair loads of ring gear-planetary gear 1

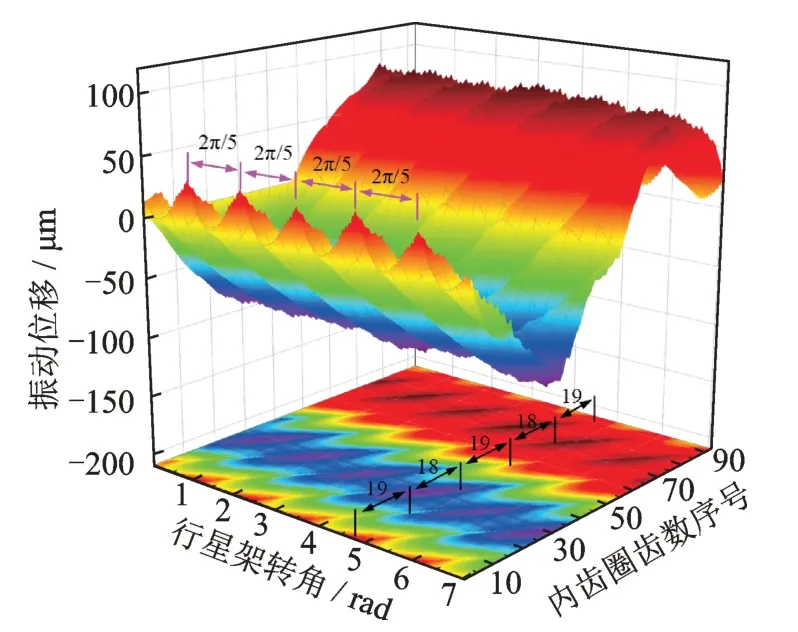
圖13 內(nèi)齒圈輪齒節(jié)點(diǎn)沿x 向的振動(dòng)位移Fig.13 Vibration displacements of ring gear tooth nodes in the x-direction

2.3 穩(wěn)態(tài)工況

2.3.1 構(gòu)件振動(dòng)

當(dāng)Tin=4×106N?m 時(shí)，太陽輪、行星輪和內(nèi)齒圈振動(dòng)位移分別如圖14～16 所示。其中，全柔模型表示本文模型（式（22）），剛性模型則是將式（22）中太陽輪軸、內(nèi)齒圈等構(gòu)件視作剛體，但仍保留行星輪系多輪齒動(dòng)態(tài)嚙合關(guān)系。從圖14～16 可知，考慮構(gòu)件結(jié)構(gòu)柔性后，太陽輪、行星輪和內(nèi)齒圈振動(dòng)位移幅值出現(xiàn)了不同程度增大。其中，內(nèi)齒圈振動(dòng)位移變化最為明顯，呈現(xiàn)大幅低頻波動(dòng)（相鄰行星輪相位與圖13 相似）和高頻振動(dòng)（齒輪嚙頻）的疊加特征；內(nèi)齒圈輪齒節(jié)點(diǎn)1 的最大振動(dòng)位移峰值出現(xiàn)在y向，其次依次為x向和z向，分別為118.4，36.8 和12.5 μm，并且觀察到x向振動(dòng)位移峰值位置超前于y向和z向。其主要原因是隨著行星架逆時(shí)針旋轉(zhuǎn)，當(dāng)行星輪與內(nèi)齒圈輪齒節(jié)點(diǎn)1 剛好嚙合時(shí)，沿著嚙合線方向的輪齒動(dòng)載荷在內(nèi)齒圈輪齒節(jié)點(diǎn)1 處x向的投影量達(dá)最大，使得x向振動(dòng)位移最早出現(xiàn)峰值；隨著行星架轉(zhuǎn)角繼續(xù)增加，輪齒動(dòng)載荷在y向的投影量逐漸增至最大值，隨后出現(xiàn)振動(dòng)位移峰值，并且在整個(gè)嚙合過程中，輪齒動(dòng)載荷沿y向的投影分量大于x向的投影分量。

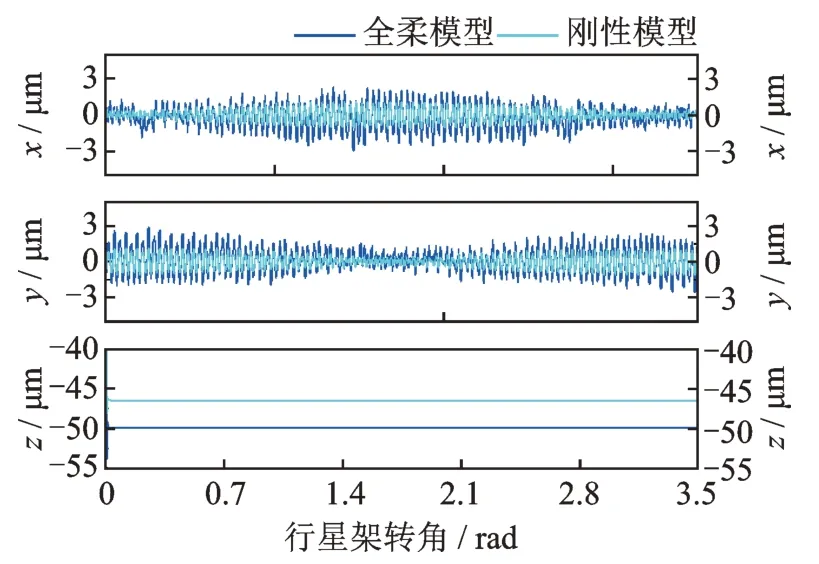
圖14 太陽輪振動(dòng)位移Fig.14 Vibration displacements of sun gear

圖15 行星輪1 振動(dòng)位移Fig.15 Vibration displacements of planetary gear 1

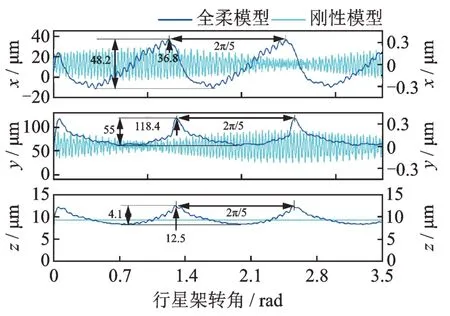
圖16 內(nèi)齒圈輪齒節(jié)點(diǎn)1 振動(dòng)位移Fig.16 Vibration displacements of ring gear tooth node 1

2.3.2 輪齒載荷

圖17 和18 分別為不同建模方式對太陽輪-行星輪1 和內(nèi)齒圈-行星輪1 嚙合副載荷的影響。其中，剛度分解表示根據(jù)嚙合剛度幅值（如圖7 所示），將全柔模型計(jì)算得到的動(dòng)態(tài)嚙合力分解到各輪齒上，進(jìn)而得到輪齒動(dòng)載荷，如下式所示：

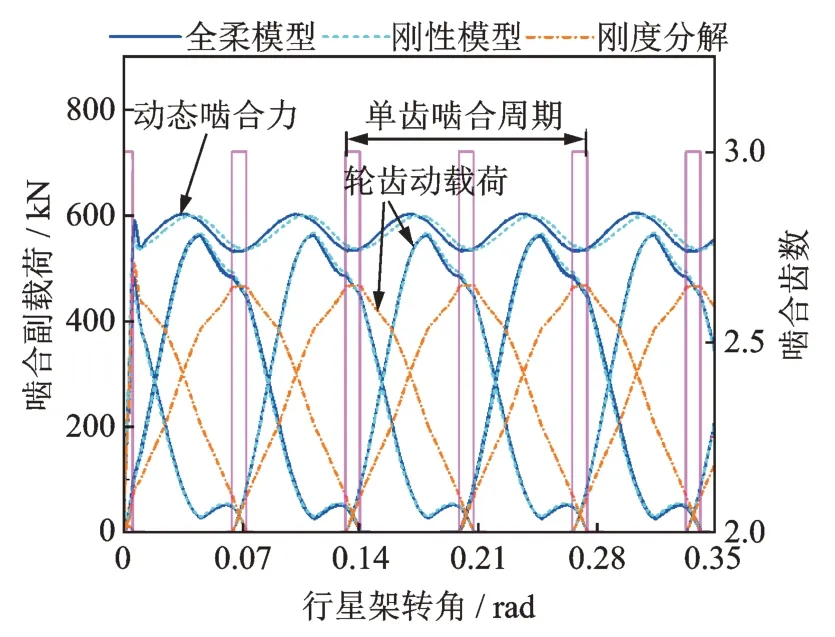
圖17 太陽輪-行星輪1 嚙合副載荷Fig.17 Meshing gear pair loads of sun gear-planetary gear 1

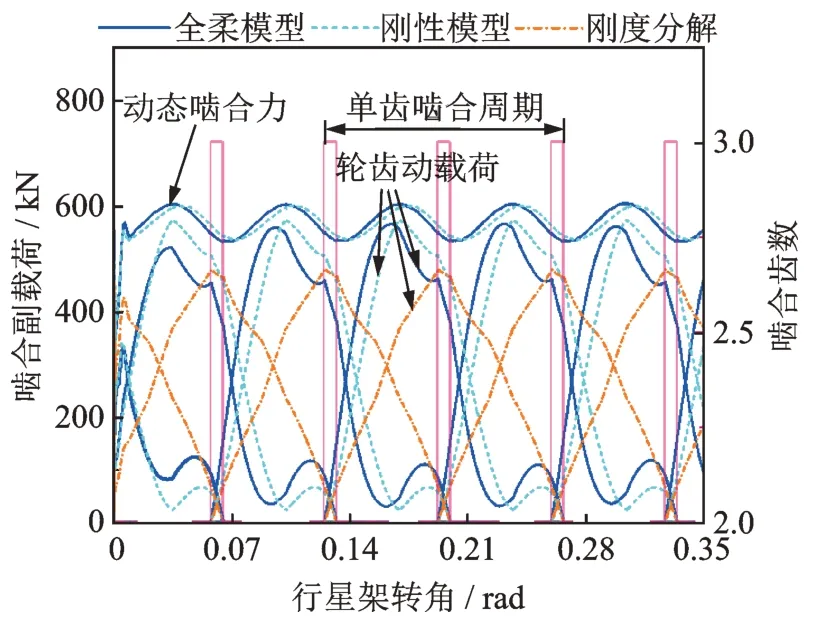
圖18 內(nèi)齒圈-行星輪1 嚙合副載荷Fig.18 Meshing gear pair loads of ring gear-planetary gear 1

從圖17，18 中可知，相較于剛度分解模式下的輪齒動(dòng)載荷，考慮多輪齒動(dòng)態(tài)嚙合狀態(tài)后，其輪齒動(dòng)載荷峰值更大，且更偏向于左側(cè)。因此若將動(dòng)態(tài)嚙合力直接按照嚙合剛度幅值簡單地分解到各輪齒上，容易低估輪齒動(dòng)載荷幅值。在同一對內(nèi)齒圈-行星輪i嚙合副中，多輪齒嚙合點(diǎn)沿嚙合線方向等間隔分布，此時(shí)嚙合點(diǎn)越靠近從動(dòng)輪（內(nèi)齒圈輪齒節(jié)點(diǎn)），內(nèi)齒圈輪齒節(jié)點(diǎn)彈性變形在該處的投影分量將會(huì)越小（即式（4）中θrj叉乘系數(shù)更小），使得對應(yīng)的嚙合副相對位移更大，加之時(shí)變嚙合剛度作用，造成相較于剛性模型，考慮構(gòu)件柔性后，內(nèi)齒圈-行星輪嚙合副的輪齒動(dòng)載荷峰值會(huì)朝左側(cè)偏移（嚙入起始點(diǎn)側(cè)）。因此，考慮內(nèi)齒圈結(jié)構(gòu)柔性有助于獲取更為準(zhǔn)確的內(nèi)齒圈-行星輪的齒輪動(dòng)載荷分布。

2.3.3 均載系數(shù)

為了描述整個(gè)行星輪系因外載荷變動(dòng)、構(gòu)件變形、時(shí)變嚙合剛度與傳動(dòng)誤差等動(dòng)態(tài)參數(shù)激勵(lì)引起的均載性能變化，行星輪系均載系數(shù)的計(jì)算式為［31］：

計(jì)算結(jié)果如圖19 所示。從圖19 中可知，相較于剛性模型，考慮構(gòu)件柔性后，行星輪均載系數(shù)增大。這是由于相較于全柔模型，剛性模型的內(nèi)齒圈被簡化為集中質(zhì)量點(diǎn)，其振動(dòng)位移幅值偏小（如圖16 所示），且無法計(jì)算因輪齒動(dòng)載荷造成的內(nèi)齒圈局部擠壓變形（如圖8（a）所示），造成計(jì)算得到的內(nèi)齒圈與5 個(gè)行星輪之間的動(dòng)態(tài)嚙合力較為理想。分析結(jié)果表明，若采用內(nèi)齒圈-行星輪嚙合副的動(dòng)態(tài)嚙合力計(jì)算行星輪均載系數(shù)（式（24）），建議在模型中考慮內(nèi)齒圈結(jié)構(gòu)柔性。

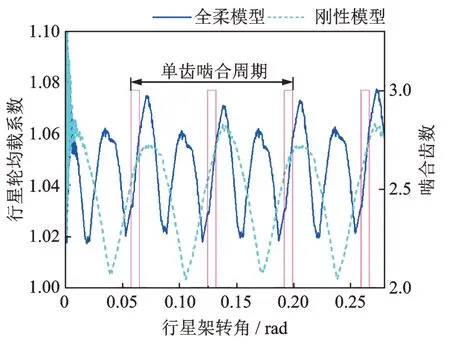
圖19 行星輪均載系數(shù)Fig.19 Load-sharing coefficient of planetary gear

2.4 變速變載工況

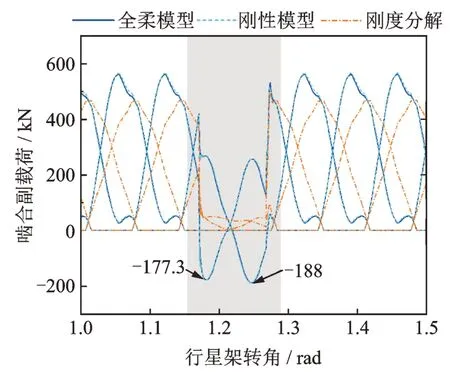
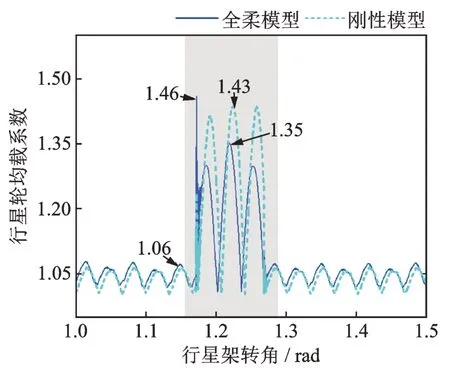
由于風(fēng)速的隨機(jī)性，風(fēng)電齒輪箱需要在變速變載工況下長期運(yùn)行。為了驗(yàn)證本文模型適用于變速變載工況，通過預(yù)設(shè)輸入扭矩產(chǎn)生突變，獲取構(gòu)件振動(dòng)位移、輪齒載荷以及均載系數(shù)。輸入扭矩預(yù)設(shè)過程：①t≤1 s 時(shí)，Tin=4×106N?m；② 1 s

2.4.1 構(gòu)件振動(dòng)

圖20～22 分別為扭矩突變工況下太陽輪、行星輪和內(nèi)齒圈的振動(dòng)位移。從圖20～22 中可知，當(dāng)輸入扭矩驟跌時(shí)，各構(gòu)件的瞬態(tài)振動(dòng)位移幅值明顯降低；全柔模型和剛性模型均可以較好地計(jì)算太陽輪和行星輪的瞬態(tài)振動(dòng)響應(yīng)；相較于剛性模型，全柔模型可以計(jì)算得到更為詳細(xì)的內(nèi)齒圈輪齒節(jié)點(diǎn)瞬態(tài)振動(dòng)響應(yīng)，有助于指導(dǎo)內(nèi)齒圈結(jié)構(gòu)優(yōu)化設(shè)計(jì)。

圖20 太陽輪振動(dòng)位移Fig.20 Vibration displacements of sun gear

圖21 行星輪1 振動(dòng)位移Fig.21 Vibration displacements of planetary gear 1

圖22 內(nèi)齒圈輪齒節(jié)點(diǎn)1 振動(dòng)位移Fig.22 Vibration displacements of ring gear tooth node 1

2.4.2 輪齒載荷

圖23 和24 分別為扭矩突變工況下太陽輪-行星輪1 和內(nèi)齒圈-行星輪1 嚙合副載荷的變化情況。從圖23，24 可知，在全柔模型中，輸入扭矩跌落會(huì)降低輪齒動(dòng)載荷，且不同輪齒動(dòng)載荷降幅存在差異，太陽輪-行星輪1 的輪齒動(dòng)載荷分別降至-177.3 和-188 kN?m，內(nèi)齒圈-行星輪1 的輪齒動(dòng)載荷分別降至-202.5 和-110.8 kN?m，這意味對應(yīng)的輪齒已發(fā)生脫齒，且容易產(chǎn)生反向接觸。剛性模型計(jì)算得到的太陽輪-行星輪嚙合副瞬態(tài)載荷變化與全柔模型計(jì)算結(jié)果差異較小；由于內(nèi)齒圈結(jié)構(gòu)柔性會(huì)吸收部分因沖擊載荷引起的輪齒節(jié)點(diǎn)振動(dòng)，造成剛性模型計(jì)算得到的內(nèi)齒圈-行星輪嚙合副中部分輪齒瞬態(tài)載荷略大于全柔模型計(jì)算結(jié)果。此外，相比于全柔模型計(jì)算結(jié)果，剛度分解模式下各輪齒動(dòng)載荷均大于零，表明該方法不適用于計(jì)算變速變載工況下的輪齒動(dòng)載荷。

圖23 太陽輪-行星輪1 嚙合副載荷Fig.23 Meshing gear pair loads of sun gear-planetary gear 1

圖24 內(nèi)齒圈-行星輪1 嚙合副載荷Fig.24 Meshing gear pair loads of ring gear-planetary gear 1

2.4.3 均載系數(shù)

圖25 所示為扭矩突變工況下行星輪均載系數(shù)的變化情況。從圖25 可知，扭矩突變會(huì)顯著增大行星輪均載系數(shù)，表明此時(shí)內(nèi)齒圈與5 個(gè)行星輪之間的動(dòng)態(tài)嚙合力出現(xiàn)了明顯差異。此外，由于柔性內(nèi)齒圈的吸振作用，造成在扭矩突變期間內(nèi)，柔性模型計(jì)算得到的行星輪均載系數(shù)明顯小于剛性模型計(jì)算結(jié)果。因此，在計(jì)算變速變載工況下的行星輪均載系數(shù)時(shí)，建議考慮內(nèi)齒圈結(jié)構(gòu)柔性，可以提高計(jì)算結(jié)果精度。

圖25 行星輪均載系數(shù)Fig.25 Load-sharing coefficient of planetary gear

3 結(jié)論

本文將行星輪系嚙合副常規(guī)等效單點(diǎn)嚙合細(xì)化至多對輪齒嚙合，通過引入嚙合副變速表征變量和內(nèi)齒圈虛擬振動(dòng)線位移，構(gòu)建了驅(qū)動(dòng)輪轉(zhuǎn)角與行星輪系多輪齒嚙合狀態(tài)的映射關(guān)系，并基于模態(tài)縮減理論，將內(nèi)齒圈輪齒與彈性支撐進(jìn)行耦合，建立計(jì)入結(jié)構(gòu)柔性的風(fēng)電齒輪箱行星輪系變速動(dòng)力學(xué)模型，分析了工況變化對嚙合副變速表征變量、構(gòu)件振動(dòng)、輪齒載荷和均載系數(shù)的影響，主要結(jié)論如下：

（1）當(dāng)5 個(gè)行星輪受力平衡時(shí)，行星輪切向變形量方向與行星架旋轉(zhuǎn)方向相反；內(nèi)齒圈輪齒節(jié)點(diǎn)瞬態(tài)變形整體呈“五角星”形狀，且會(huì)隨著行星架旋轉(zhuǎn)；行星輪系各構(gòu)件徑向受力平衡位置變化最大，軸向受力平衡位置變化較小。

（2）在穩(wěn)態(tài)工況下，內(nèi)齒圈輪齒節(jié)點(diǎn)振動(dòng)位移呈現(xiàn)大幅低頻波動(dòng)和高頻振動(dòng)的疊加特征；行星輪系輪齒動(dòng)載荷先增大后減小，整體變化趨勢與單對齒嚙合剛度相似；輪齒動(dòng)載荷會(huì)使柔性內(nèi)齒圈產(chǎn)生局部擠壓變形，影響均載性能。

（3）當(dāng)輸入扭矩跌落時(shí)，行星輪系各構(gòu)件瞬態(tài)振動(dòng)位移幅值將驟減；扭矩突變會(huì)破壞多個(gè)行星輪之間的動(dòng)載荷平衡，惡化均載性能；柔性內(nèi)齒圈可在一定程度上吸收部分因沖擊載荷引起的構(gòu)件振動(dòng)，提高行星輪均載性能。

本文方法可以直接考慮傳動(dòng)構(gòu)件復(fù)雜結(jié)構(gòu)幾何特征與多輪齒嚙合狀態(tài)，避免因簡化處理帶來的精度不足，為實(shí)現(xiàn)重載風(fēng)電齒輪箱行星輪系變速動(dòng)力學(xué)建模、提高動(dòng)態(tài)特性分析精度提供了一種有效技術(shù)手段。