深研細究　實現教學至簡

于淼紅

摘 要：好的試題往往具有良好的教學導向作用，教師應挖掘典型好題的育人功能，盤活好題資源，開發試題的教學功效，拓寬學生的思考視角，提高教學效能，使學生將知識融會貫通，輕松地學數學，實現教學至簡.

關鍵詞：至簡教學；轉化思想；解題教學

1 深研課標，細品教材

數學教材為學生的數學學習活動提供了學習主題、基本線索和知識結構，是實現數學課程目標、實施數學教學的重要資源.在教學設計之前，教師應該認真研讀課程標準，深入研讀教材，揣摩教材編寫意圖，體會教材如何承載課程目標，過程中不僅要關注數學知識本身，而且要思考知識背后蘊含的數學本質，包括數學知識的內在聯系、數學規律的形成過程、數學思想方法的提煉和數學理性精神的體驗.在此基礎上，靈活地、創造性地使用教材.本節課意圖在深入理解教材的基礎上用教材進行教學.

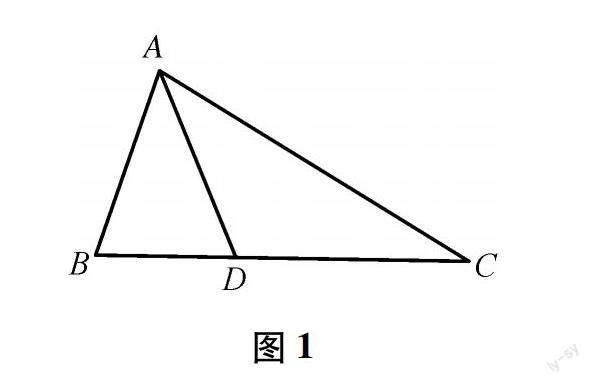
例題：（人教版八上62頁習題） 在△ABC中，AD為角平分線，∠ABC＝2∠ACB，求證：AB+BD=AC.

2 在情境引學中將思維由淺表引向深入

數學是一門訓練思維，提升能力的學科.“解法開放”是全國各地歷年中考數學壓軸題的特色之一.但只要認真探索這些數學試題，均能發現隱藏其中的“共性”，即試題大都回歸數學本源，注重通性通法，凸顯數學能力的考察.

方法探究一（核心思想一：轉換，造等角——出等腰）

在平面幾何中，相等的角有著重要價值，相等的角可以聯想到等腰三角形，可以聯想到角平分線，可以構造全等，可以構造相似等.二倍角問題又是平面幾何中的一個常見問題，也是一個難點問題，所以當二倍角出現時我們可以把二倍角轉化成相等的角，利用相等的角去解決問題.

已知條件∠ABC＝2∠ACB是解題的關鍵.現在我們來研究一下，如何處理二倍角問題.

方法1：延等腰：延長CB至D，使得BD＝AB，可以得到∠D＝∠C＝∠BAD，通過這組等角我們得到兩個等腰三角形和一個斜A相似.

方法2：截等腰：在BC邊上取點D，連接AD，使得AD＝CD，得到∠C＝∠CAD，∠B＝∠ADB，這樣通過這組等角我們可以得到兩個等腰三角形.

方法3：作角平分線：做△ABC的角平分線BD，得到∠CBD＝∠C＝∠ABD，通過這組等角我們得到一個等腰三角形，一個角平分線，一個斜A相似.

方法4：翻折：把直線CB沿AC翻折得到直線CD，設CD交BA延長線于D，得到∠B＝∠BCD，∠ACB＝∠ACD，這樣通過這組等角我們可以得到一個等腰三角形和一個角平分線.

總結：關于二倍角問題，上面介紹了四種添加輔助線的方法，主要目的都是為了構造相等的角，進而推出角平分線、等腰三角形等，然后再利用相關的性質探求解題途徑.由于種種原因，學生的思維往往處于沉睡狀態.數學教學中，教師要努力尋求問題之間的連接點、生長點，循序漸進，形成自然聯系的整體，為思考鋪路，為探究引航，不斷喚醒和激活思維，引導學生進行深度學習，讓學生建立“屬于自己”的知識結構、思維方式和學習經驗.

例題賞析

例1 在△ABC中，AD為角平分線，∠ABC＝2∠ACB，求證：AB+BD=AC.

方法1：延等腰：如圖7，延長AB至E，BE＝BD，連接DE，△ADE≌△ADC，AE＝AC，所以AC＝AB +BD.

方法2：截等腰：在AC邊上截取AE＝AB，則△ABD≌△AED，易得BD＝DE＝CE，所以AC＝AB + BD.

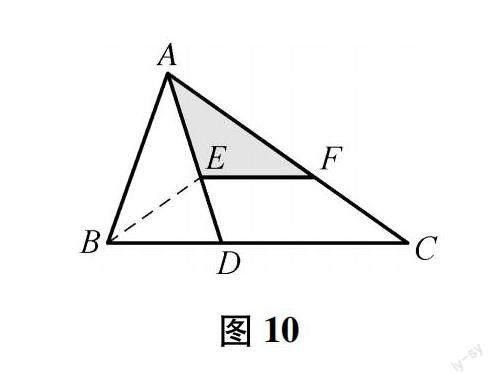
方法3：作角平分線：過B做BE平分∠ABC交AD于E，EF平行BC交AC于F，導角得BD＝BE，易證△ABE≌△AFE，所以AB＝AF，易得CF＝BE，所以AC＝AB+BD.

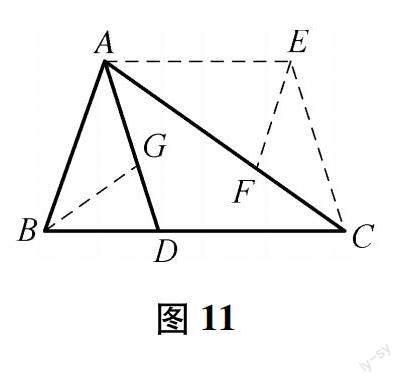
方法4：翻折：把直線CB沿AC翻折得到直線CE，AE∥BC，得到∠ABC＝∠BCE，∠ACB＝∠ACE，易得AB＝CE＝AE，在AC上取點F，在AD上取點G，使得AF＝AE、BG＝BD，△BGA≌△CFE，所以BD＝BG＝CF，所以AC＝AB+BD.

通過這一道教材習題，聚焦基本圖形，深入引導學生挖掘基本圖形中隱含的數學知識.這一過程在學生數學現實的基礎上，利用問題引導學生感受發現數學知識的過程，通過從特殊到一般、從具體到抽象的引導過程激發學生深度思考，促進高階思維的發生.

3 探究研學，激發思維

專題探究課應注重層層深入、揭示問題的本質，促進學生思維深入發展.蘇聯教育家霍姆林斯基說：“只有讓學生在認知過程中感受自己的智力，體會到創造的愉快，才能激發學生高昂持久的興趣.”本節課通過有效設置問題變化情境，精心設計探究過程，有效組織探究活動，引導學生科學有序地對模型本質進行探究.

例2 如圖12，在△ABC中，∠B＝2∠C，求線段AB、BD與CD的數量關系.

方法1：延等腰：延長CB至E，使得BE＝AB，得到∠E＝∠C＝∠BAE，易得DE＝CD，所以AB+BD＝CD.

方法2：截等腰：在BC邊上取點E，連接AE，使得AE＝CE，得到∠C＝∠CAE，∠B＝∠AEB，所以BD＝DE，AB＝AE＝CE，所以AB+BD＝CD.

方法3：作角平分線：過B做BE平分∠ABD交AD于E，EF∥BC交AC于F，在線段AF上取點G，AE＝EG，可證△BDE≌△CHF，△ABE≌△EFG，所以BD＝CH，AB＝EF＝DH，所以CD＝AB+BD.

方法4：翻折：把直線CB沿AC翻折得到直線CE，AE∥BC，得到∠B＝∠BCE， ∠ACB＝∠ACE，易得BD＝CF，AB＝DF，所以CD＝AB+BD.

高階思維的發生需要問題的驅動.如何從學生的數學現實出發設置問題，開展有效的思維活動？如何通過問題引導，讓學生在解決問題的過程中感悟數學思想方法？如何讓學生體會到習題課中的思維升華，通過類比、拓展實現思維創造，生成數學知識，積累基本經驗，基于以上思考，本節課的問題引導從特殊到一般，從方法類比到圖形構造.在問題引導中溯源問題本質，在思想方法的感悟中探求新知，讓學生經歷知識的形成、鞏固和深化的過程.

方法探究二：（核心思想二：導特殊）

有一些二倍角的問題中往往隱藏了某種特殊，可以是隱藏特殊三角形，特殊角，特殊關系，需要我們導角把特殊找到，然后根據特殊解決問題.

例題賞析

例3 如圖17，在△ABC中，AD為高線，BD＝2，CD＝3，∠BAD＝2∠C，求線段AD的長度.

解析：如圖，設∠ACB＝x，則∠BAD＝2x，∠CAD＝90°-x，∠BAC＝90°+x，導出AC為△ABD的外角平分線，所以過C做CE⊥AB于E，所以CE＝CD＝3，勾股定理得BE＝4，得到∠B的正切值，所以AD＝1.5.

總結：本題就是通過導角得到一個特殊條件：AC為角平分線，然后利用角平分線的相關性質解決問題.

例4 如圖19，在△ABC中，D、E分別在AB、AC邊上，AD＝CD，∠CDE＝60°，∠ADE＝2∠BCD，BD＝3，DE＝5，求線段CE的長度.

解析：如圖設∠BCD＝x，則∠ADE＝2x，∠ACD＝60°-x，∠ABC＝60°+x，所以∠ACB＝60°，得到特殊角∠ACB，延長DE至F，使得DF＝CD，連接CF，在BC邊上截取DG＝DB，可證△CFE≌ △CDG，所以BD＝DG＝EF＝3，DE＝5，∠F＝60°，△CEF可得CE＝7.

綜上所述，處理二倍角問題的思想主要是：一是造相等，構造出相等的角，利用等角處理問題;二是導特殊，導出特殊關系，利用特殊關系解決問題.

4 培養遷移能力，訓練數學思維

學習遷移是指學生在學習過程中把之前學習的知識或解決問題的能力自覺地應用到新知識的學習和實際問題的解決中.通過學習遷移能力的培養，可以有效提升學生的學習效率，優化思維品質，為學生終身發展打好能力基礎.

例5 在△ABC中∠C=60°，D、E分別在BC、AC上，AD=AB，AE=EB.

（1） 求證∠ADE=30°.

（2） 點M在CB的延長線上，DM=AE，AM=c，AD=b，DE=a，試確定a、b、c的數量關系.

解析：（1） ［對稱法］α，α+60°，60°-2α.

［法1］中垂線GEF，［369△AGF］，兩個α，AF＝2AG＝AB＝AD，△AED和△AEF全等［SAS］，兩個30°.

［法2］F、B關于AC對稱，正△ADF，△ADE和△FDE全等［SSS］，兩個30°.

（2） ［等邊轉換與角度轉換］

［法1］∠EBA＝∠EAB＝60°-α，∠ABD＝∠ADB＝60°+α，∠DBE＝2α ∠EDC＝90°-α，作BN＝BE，則DE＝EN＝α，DN＝MB＝n ［美人魚相似］△NDE∽△NEB［AA］，a²＝n（n+2m）.

［雙勾股］c²-b²＝（n+m）²-m²＝n（n+2m），故a²＝c²-b².

［法2］正△AMN，［對頂點O］兩個θ，兩個黃色三角形全［SAS］正△DNE，Rt△ADN，c²＝a²+b².

5 深度反思，內化思想

反思1：通過本節課可以看出，活動內容只是探究的一個載體，經過探究活動，學生能發現其中的數學本質、找出其中的數學規律，從而帶動思維能力的發展.筆者通過對課堂探究教學的嘗試與反思，意識到探究教學不是對數學內容的機械重復，而是對數學內容的重置與延伸.

反思2：熟練解題模型，提煉解題規律.解體模型是指教師在解題教學中發現并總結出一些結論性認識，具體指一般化程度較高的結論或圖形.G·波利亞認為，解決一個問題之后，要善于去總結一個模型，并井然有序地儲備起來，以后才可以隨時支取它去解決類似的問題，進而提高自己的解題能力.如本題解決二倍角問題用到的幾個基本模型.教師不僅要熟悉一些常見的解題模型，還要在解題教學中指導學生總結提煉解題規律，培養學生良好的解題直覺，啟迪學生思考方向，進而順利解決問題.

反思3： 著名數學教育家弗賴登塔爾曾說過：“與其說讓學生學習數學，不如說讓學生學習數學化.”意思是學生學習數學的終極目標應該是形成自己的數學思想和方法，學會用數學的眼光去看待事物，學會用數學的方法解決問題.因此我們的教學，不應該僅僅是一節課做完這一題及其變式就了結.我們還應做好梳理總結工作，反思本節課中問題的解決路徑、運用的數學知識和思想方法.除了課后反思這一重要環節，教師還需要引導學生在問題解決的核心處深度思考、深切體驗數學思想方法的滲透.這便是學生從數學的知識學習走向數學思維化學習的必經之路.

反思4：好的試題往往具有良好的教學導向作用，深研細究試題的內涵并盤活類似的學習資源，能開發試題的教學功效，拓寬學生的思考視角，提高教學效能，使學生將知識融會貫通，輕松地學數學，實現教學至簡.

參考文獻：

［1］ 王眉燕.滲透數學思想方法，培養數學核心素養［J］.數學教學通訊，2017（13）：55-56.