路徑積分傳播子測量的研究進展*

田禮漫 溫永立? 王云飛 張善超 李建鋒 杜鏡松 顏輝3) 朱詩亮3)

1)(華南師范大學物理學院,原子亞原子結(jié)構(gòu)與量子調(diào)控教育部重點實驗室,廣州 510006)

2)(華南師范大學,廣東省量子調(diào)控工程與材料重點實驗室,廣州 510006)

3)(華南師范大學物理前沿科學研究院,粵港量子物質(zhì)聯(lián)合實驗室,廣州 510006)

傳播子在路徑積分理論中扮演著核心角色,因此在路徑積分理論可使用的多個現(xiàn)代量子物理領域中有重要價值.然而,由于其一直未能在實驗中被直接測量,基于路徑積分表述研究量子系統(tǒng)的實驗進展受到了嚴重制約.最近,基于波函數(shù)直接測量方法,我們提出了傳播子測量方案,并利用單光子實驗首次成功實現(xiàn)了傳播子的實驗測量.此外,在這項研究中還首次演示了量子力學的最小作用量原理.該研究成功解決了路徑積分實驗研究中的技術(shù)難題.本文綜述了此領域的研究進展,具體為簡述波函數(shù)直接測量的基本概念和研究進展,并詳細介紹傳播子測量的理論模型、實驗設計和實驗結(jié)果.最后,介紹了一個重要的應用范例,即通過傳播子測量實現(xiàn)最小作用量原理的實驗演示.本文綜述的傳播子測量研究進展,將為今后使用該方法開展相關(guān)實驗研究提供重要的參考.

1 引言

1948年,費曼根據(jù)最小作用量原理提出了量子力學的路徑積分表述[1-3],這是繼薛定諤的波動力學和海森伯的矩陣力學之后的第三種量子力學表述方式.路徑積分對現(xiàn)代量子物理學的發(fā)展發(fā)揮了巨大作用,是量子場論、量子統(tǒng)計、量子引力等多個領域的基礎.傳播子是路徑積分理論的核心物理量,它是獲取量子系統(tǒng)重要信息(如波函數(shù)、量子態(tài)演化、作用量、拓撲不變量和配分函數(shù))的重要工具.然而,自從提出路徑積分以來,其主要作為研究量子系統(tǒng)的理論工具,實驗研究基本空缺.基于路徑積分表述的量子實驗需要對傳播子進行測量,但在我們的工作[4]之前,國際上未有關(guān)于傳播子測量的實驗報告,這是限制路徑積分實驗研究推進的主要原因.

傳播子描述了量子系統(tǒng)從初態(tài)演化到末態(tài)的概率幅,與波函數(shù)一樣,都是復值.而傳統(tǒng)的正交投影量子測量模型[5]僅能對實數(shù)物理量進行測量.1988 年Aharonov 等[6]提出了弱測量概念,他們發(fā)現(xiàn)在該測量框架下,弱值可以把測量信號顯著放大,這種放大效應后來被廣泛應用于量子精密測量和微小量測量中.2011 年Lundeen 等[7]巧妙利用弱值是復值這個性質(zhì),把弱值與波函數(shù)進行關(guān)聯(lián),最終把波函數(shù)的實部和虛部分別對應到實驗可探測量中,實現(xiàn)了對單光子空間波函數(shù)的直接測量.這種測量方法具有簡潔、直接的優(yōu)勢,也被稱為直接測量法,被廣泛應用到各類量子態(tài)測量實驗中,也有不少研究對這種測量技術(shù)進行了重要的推廣和優(yōu)化.由于傳播子和波函數(shù)在數(shù)學形式和物理性質(zhì)方面具有相似性,我們自然可以問一個重要科學問題:是否可以基于波函數(shù)的直接測量方法來研究傳播子的實驗測量方法? 我們研究組[4]于2017 年開展了此問題的研究,并于2023 年發(fā)表了研究結(jié)果:基于波函數(shù)的直接測量方法,提出了實現(xiàn)路徑積分傳播子測量的理論模型;類似波函數(shù)的直接測量方法,傳播子的實部和虛部分別從可測量算符的期望值得到.根據(jù)這個理論模型,我們基于單光子設計了傳播子的實驗測量系統(tǒng),成功測量了單光子在自由空間及諧振勢中的傳播子,這是傳播子的首次實驗測量,為基于路徑積分的實驗研究解決了關(guān)鍵的技術(shù)問題.此外,該研究基于傳播子的測量對路徑積分中的最小作用量原理進行了演示,通過測量所得的傳播子進行分析,得到了單光子的經(jīng)典路徑,首次實現(xiàn)了量子力學中的最小作用量原理實驗演示.傳播子是現(xiàn)代量子物理中的重要物理量之一,對其進行實驗測量為未來基于路徑積分的量子系統(tǒng)實驗研究提供了方法,是推動路徑積分從理論研究逐步走向?qū)嶒炑芯康耐緩?

本文旨在綜述傳播子測量方法的相關(guān)研究進展.第2 節(jié)概述弱值的概念、波函數(shù)直接測量法及其進展,重點介紹該方法實現(xiàn)復值物理量測量的主要思想.第3 節(jié)簡要介紹最小作用量原理的沿革以及路徑積分理論和傳播子的基本概念.第4 節(jié)先介紹傳播子測量的理論模型,然后以光學系統(tǒng)為例介紹實現(xiàn)傳播子測量的實驗設計,并展示測量所得傳播子實驗數(shù)據(jù).第5 節(jié)介紹基于傳播子的測量實現(xiàn)最小作用量原理實驗演示,這是傳播子測量的重要應用范例.最后,對傳播子測量的研究進行總結(jié)并展望未來的研究方向.

2 波函數(shù)的直接測量法

波函數(shù)是描述量子系統(tǒng)狀態(tài)的復值函數(shù),通過波函數(shù)可得出量子系統(tǒng)的各種性質(zhì),是量子理論的核心.一般而言,量子可測量的算符是厄密算符,測量結(jié)果也必為實數(shù),而波函數(shù)是復數(shù),通過傳統(tǒng)的正交投影測量方法難以對其直接測量,量子態(tài)層析[8,9]是測量波函數(shù)較成熟和常用的方法,它通過對一系列算符的投影測量結(jié)果重構(gòu)出系統(tǒng)的密度矩陣或波函數(shù).然而,量子態(tài)層析有局限性,由于它需要大量的測量次數(shù)和復雜的重構(gòu)算法,在高維度量子態(tài)測量中復雜度較高.近年來,一種基于弱值來直接測量波函數(shù)的方法被提出.弱值是弱測量模型中的概念,一開始研究者們主要關(guān)注弱值的信號放大效應.后來,弱值是復值的這個特性被應用到波函數(shù)的測量中,這種測量方法因為具有簡潔和直接的優(yōu)勢而受到廣泛的關(guān)注,其測量方案和技術(shù)也在后續(xù)很多研究工作中得到了優(yōu)化與推廣.本節(jié)先介紹弱值與弱測量的基本概念,然后介紹基于它們發(fā)展出來的波函數(shù)直接測量方法的研究進展.

2.1 量子弱測量

這里k是一個與x無關(guān)的常數(shù),因此便得到了波函數(shù)ψ(x) 與弱值的正比關(guān)系,只要測量出弱值便能得到波函數(shù).而弱值則可以由指針態(tài)的湮滅算符期望值得出:

這種測量方法具有簡便性和直接性,待測波函數(shù)直接正比于實驗可觀測量,不需要大量的投影測量次數(shù)和復雜的重構(gòu)算法,因此稱為直接測量法.隨后,直接測量法得到了廣泛的應用和推廣,例如,它在光子偏振態(tài)[30]、光子軌道角動量態(tài)[31]、密度矩陣[32]、Bohmian 軌跡[33-35]、高維度量子態(tài)[36]、糾纏量子態(tài)[37]、多粒子量子態(tài)[38]、幾何相位[39]等多個領域的測量中得到應用,也有研究提出了免掃描的直接測量法[40],大大提升了高維量子態(tài)的測量效率,此外,研究者們也對這種方法進行了深入討論以及推廣[41-51].

2.2 任意耦合強度的直接測量法

基于弱值對波函數(shù)直接測量的方法要求待測系統(tǒng)與指針的耦合足夠小,這樣會導致從指針提取待測系統(tǒng)信息的信號強度很弱,在一些噪聲較大的系統(tǒng)中難以獲得較好的信噪比.2016 年Vallone 和Dequal[52]的研究發(fā)現(xiàn),波函數(shù)直接測量法中弱耦合并不是必要的,這個耦合可以是任意強度.特別是,當系統(tǒng)和測量儀器之間的耦合最大時,這種強測量的測量精度優(yōu)于弱測量,同時還保留了弱測量方案中的簡潔性和直接性.這里以空間波函數(shù)測量的模型為例,在沒有弱耦合近似的情況下,待測系統(tǒng)和指針相互作用的演化算符可表示為

其中?(0) 是與x無關(guān)的常數(shù),|1〉〈1| 是指針態(tài)|1〉的投影算符.對比(4)式和(6)式,實驗觀測結(jié)果和待測波函數(shù)之間少了 1/sinθ這個系數(shù),由于在弱測量情況下 sinθ是一個小量,強測量方案的信號強度比弱測量方案有著 1/sinθ倍的放大,因此強測量方案的測量精度也就相應得到了顯著提升.由于強測量方案具備明顯的優(yōu)勢,后來也被廣泛地應用,例如,應用在光子時域波函數(shù)的測量[53]、光子二維橫向空間波函數(shù)測量[54]、高維波函數(shù)[42,55-57]以及混合態(tài)的測量[58,59],也有研究者在離子系統(tǒng)中觀察到從弱測量到強測量的過渡[60].

3 最小作用量原理和費曼路徑積分

3.1 最小作用量原理沿革

最小作用量原理被科學家看作是物理學,甚至是自然界中最具普適性的基本原理,它具備簡潔和統(tǒng)一的科學美學特征,在物理學乃至科學發(fā)展史中有著極其重要的地位.自然界總是以最節(jié)省的方式達到它的目的,這就是最小作用量原理的核心思想.這個原理以及其變體幾乎滲透到物理學中的每個角落.

最小作用量原理在物理學中的應用可追溯到費馬原理.17 世紀,費馬在研究光的折射現(xiàn)象時提出,“光的傳播總是沿著花費時間最小的路線”,這是最小作用量原理思想研究自然界問題的第一個成功范例.其后,科學家莫培督(Maupertuis)對這種極值思想進一步推廣和總結(jié),他認為,“自然界總是以一種最節(jié)省的方式運行”,并提出了作用量的概念,為最小作用量原理的數(shù)學形式構(gòu)建了一個雛形.幾乎同一時期,歐拉也基于這種極值思想提出了物體運動的變分方程,拉格朗日受歐拉的啟發(fā),得出了分析力學的核心方程—歐拉-拉格朗日方程,后來數(shù)學家哈密頓將其總結(jié)成為哈密頓原理:

這是后來物理學中最小作用量原理常用的數(shù)學形式.

19 世紀末,著名物理學家亥姆霍茲(Helmholtz)把最小作用量原理應用于熱力學和電動力學,并證明據(jù)此可以推導出麥克斯韋方程組.他進一步把該原理看作是支配整個物理學領域統(tǒng)一的基本原理,即試圖把這一原理推廣到物理學的所有領域中,他提出,“最小作用量原理很可能是關(guān)于一切自然過程的普遍性原理······它作為具有啟發(fā)性和指導性的原理,在我們尋求新現(xiàn)象的規(guī)律時將具有極高的價值”.此后,普朗克、諾特、希爾伯特、薛定諤、費曼等眾多物理學家或數(shù)學家在亥姆霍茲指引的方向上不懈努力,取得了豐碩的成果,極大地推動了現(xiàn)代物理學的發(fā)展.歷史上有一個故事,數(shù)學家希爾伯特知道了愛因斯坦關(guān)于廣義相對論研究的初步思想后,利用最小作用量原理,比愛因斯坦還早十幾天推導出廣義相對論場方程,即現(xiàn)在稱為愛因斯坦-希爾伯特場方程的廣義相對論場方程.另一方面,數(shù)學家諾特把該原理和對稱性結(jié)合,推導出諾特定理,給出了物理學中的另一塊基石——對稱性和守恒律的關(guān)系.因此,最小作用量原理擔當著物理學的核心角色,它可以推導出物理學中幾乎全部關(guān)鍵的物質(zhì)運動方程.

3.2 路徑積分與傳播子

路徑積分[3]是量子力學的一種表述方法,其完整方法框架由理查德 · 費曼[1]于1948 年提出,它以最小作用量原理[61]為核心,通過傳播子和路徑的泛函積分來描述量子系統(tǒng)的運動和演化.路徑積分在量子物理的發(fā)展中具有承前啟后的作用,一方面,它通過最小作用量原理形象地描述了經(jīng)典力學和量子力學的關(guān)聯(lián),另一方面,它把時間和空間同等化處理,更易于從非相對論推廣到相對論的協(xié)變形式,因此極大地推動了現(xiàn)代量子場論的發(fā)展.

對于那些作用量S遠大于 ? 的路徑,它們的概率相等,但是相位變化劇烈,在疊加之后其貢獻相干相消.當一條路徑與其臨近路徑在一級近似上全都給出相同相位時,這些路線不會相互抵消,而是干涉相長,這就是最小作用量原理δS0 確定的路徑.在宏觀世界中,? 是一個趨近于0 的微小量,作用量與它的比值S/? 便趨近于無窮大,路徑很容易相消,只有滿足δS0 的路徑才是穩(wěn)定的路徑,因此宏觀世界中物體運動軌跡就是唯一確定的.路徑積分以一種簡潔、圖像化的方式重新詮釋了量子力學,它通過最小作用量原理解釋了經(jīng)典力學與量子力學之間的“過渡”[62].路徑積分在提出以后,在物理學的多個關(guān)鍵領域有著重要的影響[63-74].

4 傳播子的直接測量

4.1 傳播子測量理論方案

此時,對系統(tǒng)進行后選擇,將系統(tǒng)投影到空間位置的本征態(tài) 〈xm|,這樣指針末態(tài)|f〉〈xm|?t〉便可以寫為

最后就能得到傳播子:

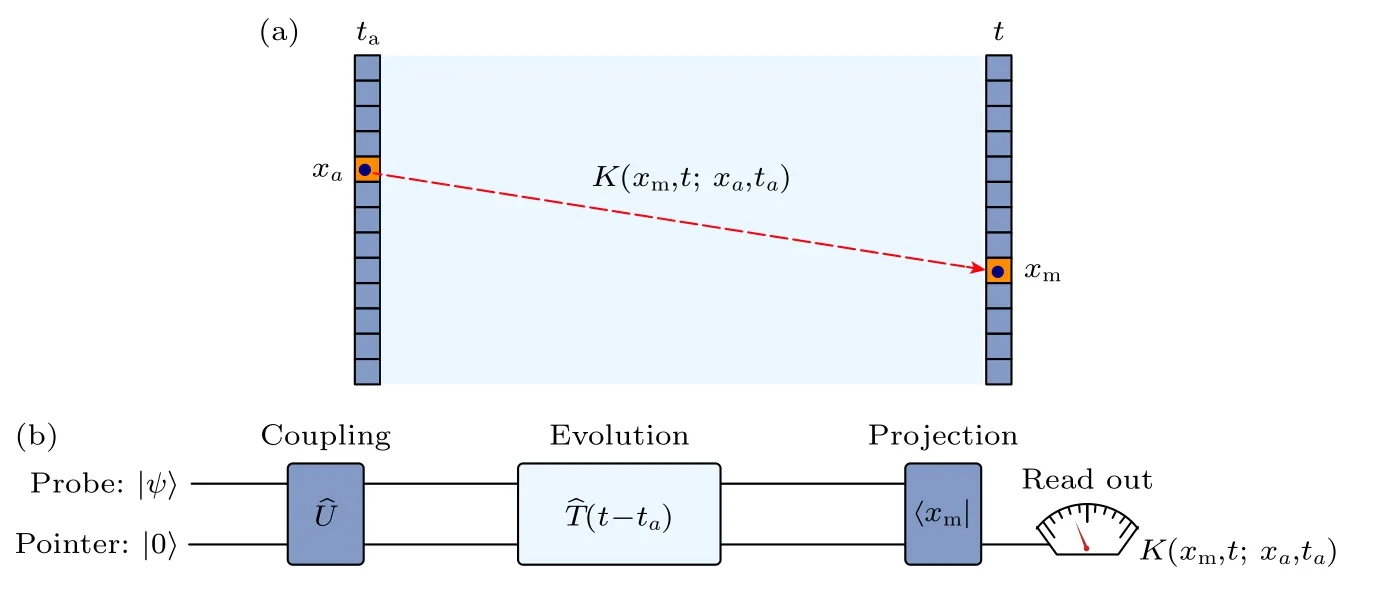
圖1 路徑積分示意圖及測量方法(a) 傳播子,粒子從(xa,ta) 傳播到(xm,t) ;(b)測量傳播子的量子線路.為了測量K(xm,t;xa,ta),首先需要制備量子態(tài)|ψ〉和指針|0〉.然后,在 ta 時刻,耦合操作 將系統(tǒng)的位置波函數(shù)與指針進行耦合.演化之后,將系統(tǒng)投影到t 時刻的位置 xm上,從指針讀出K(xm,t;xa,ta)Fig.1.Path integration diagram and measurement method:(a) Propagators:the propagation from(xa,ta) to(xm,t) ;(b) protocol to measure the propagators.To measure K(xm,t;xa,ta),the quantum state|ψ〉and pointer|0〉are prepared first.Then,at time ta,a coupling operation couples the positional wave function of the probe system with the pointer.After the evolution,the system is projected to position xm at t,and K(xm,t;xa,ta) can be read out from the pointer.

通過測量處于位置xm和時間tz/c(c為真空中光速)處的指針態(tài)結(jié)束演化.最終得到傳播子的表達式為

4.2 直接測量傳播子的實驗設計

根據(jù)4.1 節(jié)的傳播子測量方案,可設計測量傳播子的實驗.在4.1 節(jié)的傳播子測量方案中,需要對待測系統(tǒng)的空間模式和一個二維指針進行耦合,并且還需要對待測系統(tǒng)進行位置后選擇,由于光子的空間模式調(diào)控和測量的技術(shù)和設備相對較成熟,且光子的傳播與演化受到環(huán)境的影響較小,因此比較適合用于演示上述傳播子的測量方案.下面基于光學系統(tǒng)介紹實現(xiàn)傳播子測量的實驗設計.

把pz看成一個常數(shù),演化時間就與z方向的位置成正比:tz/c,c為真空中光速.這里僅考慮x方向的演化,波函數(shù)ψ(x,t) 可以用類薛定諤方程描述:

4.3 傳播子實驗測量結(jié)果

本節(jié)介紹傳播子實驗測量結(jié)果.對比文獻[4]中的單光子實驗結(jié)果,本文中的數(shù)據(jù)是之前未發(fā)表的相干光數(shù)據(jù),在實驗設計上也稍有不同.原則上本文介紹的實驗由光的一階關(guān)聯(lián)函數(shù)確定,相干光和單光子的實驗現(xiàn)象一樣,但單光子的實驗難度更大.

對于光子的傳播而言,勢能函數(shù)與折射率相關(guān).測量自由空間中的傳播子,可以讓光子在空氣中傳播,對應于圖2 所示的實驗系統(tǒng),僅需要把圖2(b3)中的漸變折射率透鏡移除即可.在此情況下,光子自由演化的哈密頓量為/(2m).自由空間中,光子從起點(xa,ta) 傳播至(x,t) 的傳播子表達式為

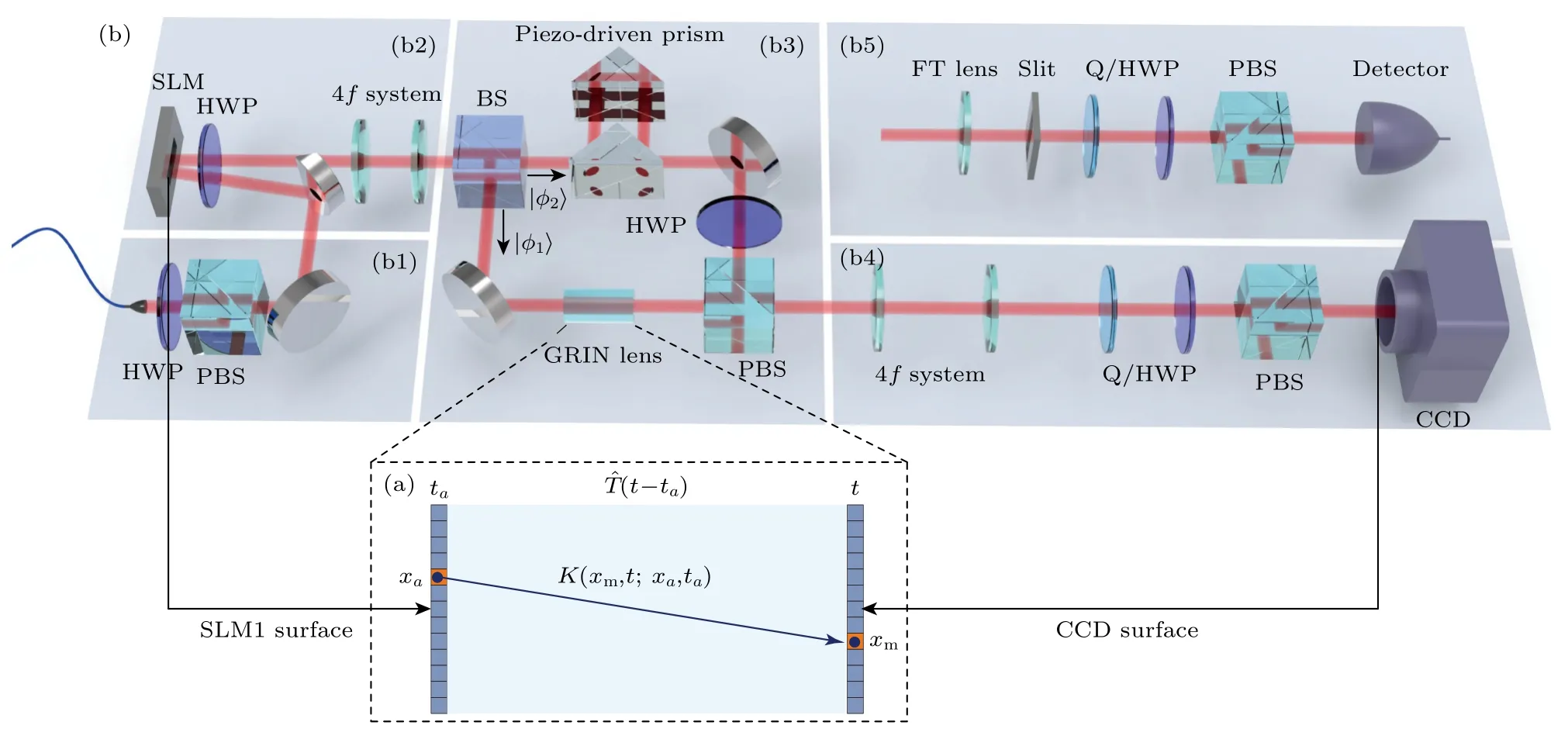
圖2 實驗示意圖(a)演化和探測區(qū)域;(b1)初態(tài)制備;(b2)系統(tǒng)位置波函數(shù)與指針耦合;(b3)態(tài)的演化;(b4)位置的后選擇與指針的讀出;(b5)波函數(shù)的測量Fig.2.Schematic diagram of the experiment:(a) The evolution and detection region;(b1) initial state preparation;(b2) coupling of wave function and pointer;(b3) state evolution;(b4) post-selection of position and the readout of the pointer;(b5) measurement of the wave function.

其中Δtt-ta.假設ta0 為初始時刻,選擇xa0的位置作為固定的初始點,通過調(diào)整圖2中CCD 的縱向位置可以調(diào)節(jié)t.CCD 在4 個不同偏振態(tài)(|+〉,|-〉,|R〉,|L〉) 的成像可測得K′′(x,t;xa,ta)ψ*(x,ta)ψ(xa,ta)K(x,t;xa,ta),圖3 給出了t20 mm/c時K′′(x,t;xa,ta)和ψ(x,ta)的實驗結(jié)果.因為傳播子類似于波函數(shù),不同的全局相位并不改變其物理實質(zhì),因此對于固定的起點而言,ψ(xa,ta) 可看作是一個常數(shù),通過對傳播子進行歸一化便可忽略此項,無需額外對其進行測量.通過K′′(x,t;xa,ta)和ψ(x,ta) 便能得到K(x,t;xa,ta).

圖3 t20 mm/c(c 為真空中的光速)的K′′(x,t;0,0)和波函數(shù) ψ(x,0) 的實驗測量結(jié)果.藍色方塊和紅色圓點分別展示了 K′′(x,t;0,0) 的實部和虛部.綠色菱形和紫色三角形分別展示了 ψ(x,0) 的實部與虛部Fig.3.Measured wave function of single photon and K′′(x,t20 mm/c;0,0).The green diamond and purple triangle represent the real and imaginary parts of the wave function,respectively.The red dot and the blue square show the real and imaginary parts of the K′′(x,t20 mm/c;0,0) at t20 mm/c.

圖4 給出了在固定初始位置xa0 和初始時刻ta0 的情況下,Kf(x,t;xa,ta) 以x和t為變量的理論和實驗的結(jié)果對比.實驗中通過改變探測器CCD 的位置來改變演化時間t,從t0 mm/c到t30 mm/c每隔 1 mm/c測量出Kf(x,t;xa,ta)以x為變量的曲線,圖4(a)和圖4(b) 分別是通過(20)式計算得到的Kf(x,t;xa,ta) 的實部和虛部的理論結(jié)果,圖4(c)和圖4(d)分別是實驗測得的Kf(x,t;xa,ta)的實部和虛部.

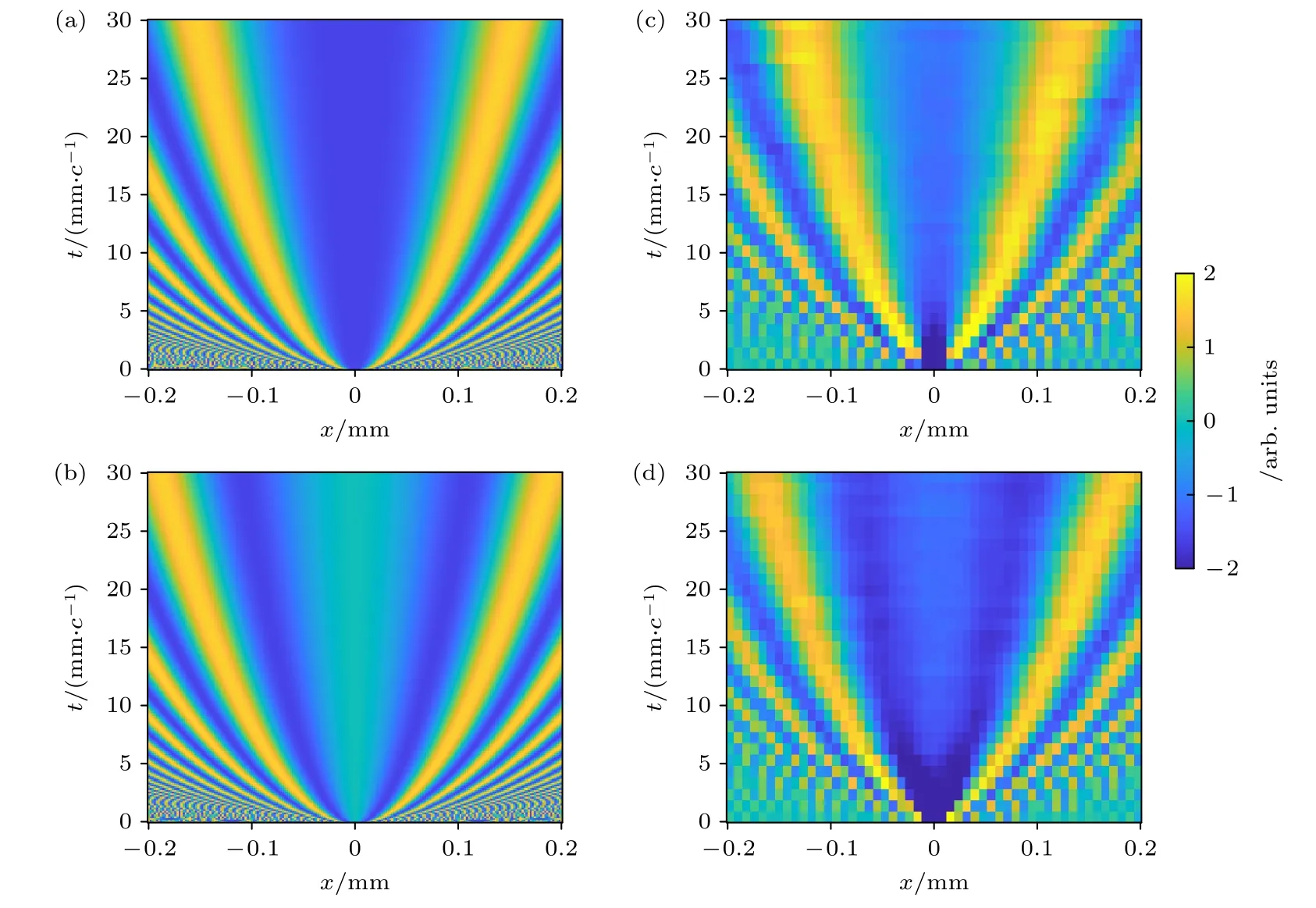
圖4 Kf(x,t;xa,ta) 以x 和t 為變量的理論與實驗結(jié)果.縱軸是演化時間t,橫軸是橫向位置x,顏色代表實部或者虛部的幅度大小.對演化時間t 每間隔1 mm/c從0 測量到30 mm/c,橫向位置每間隔8 μm從-0.2 mm 測量到0.2 mmFig.4.Theoretical and experimental results of Kf(xb,tb;xa,ta) over time.The vertical axis is the evolution time t,the horizontal axis is the transverse position x.The colormaps represent the magnitude of the real or imaginary part of Kf(x,t;xa,ta).Evolution time is measured from 0 to 30 mm/c at 1 mm/c interval.Transverse positions are measured from -0.2 mm to 0.2 mm at 8 μm intervals.

圖5 所示為圖4 中選取t{10 mm/c,20 mm/c,30 mm/c} 這3 個特定時刻的Kf(xb,tb;xa,ta) 的理論和實驗結(jié)果,紅色和藍色的實線表示傳播子實部和虛部的理論曲線,紅色的圓點和藍色的方塊是實驗測到的數(shù)據(jù),誤差棒是3 次重復測量得到的標準差.為了更準確地對比理論和實驗的結(jié)果,以實驗測量的傳播子在x0 位置的相位為準,圖4 和圖5 的理論計算結(jié)果都整體乘以一個相位因子,使得理論結(jié)果和實驗結(jié)果的全局相位統(tǒng)一.從圖4 和圖5 可以看出,Kf(x,t;xa,ta) 的實驗測量結(jié)果與理論計算結(jié)果高度吻合,這說明4.1節(jié)和4.2 節(jié)所述的理論和實驗方案可以準確地測量出傳播子.

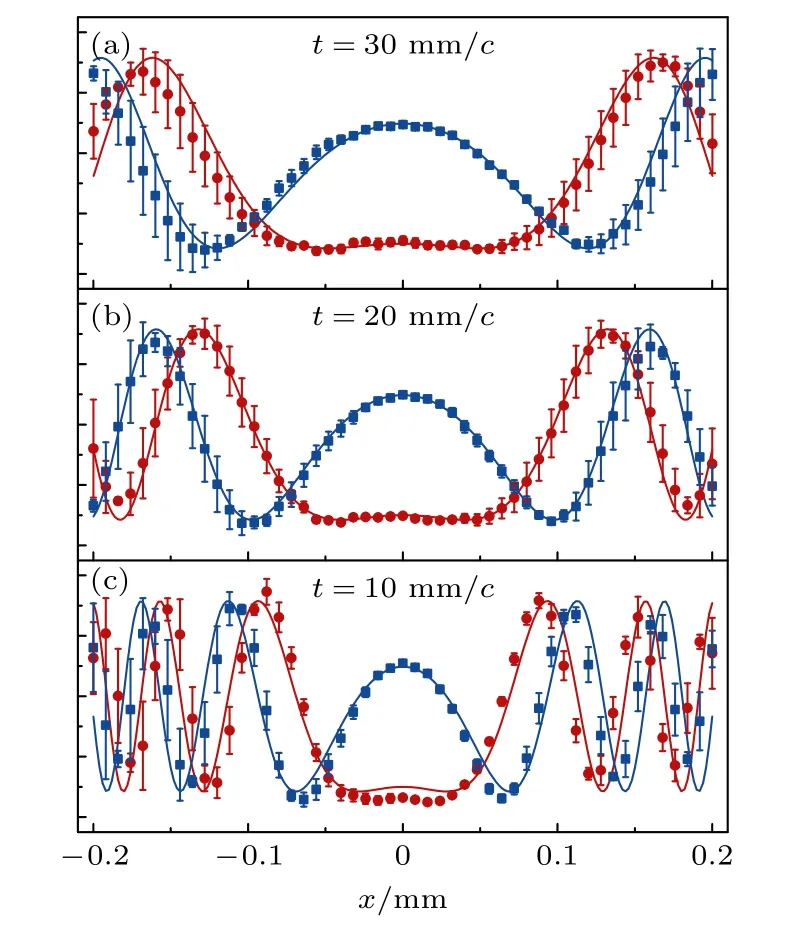
圖5 在自由空間中測到的傳播子 紅線和藍線是理論計算的傳播子實部和虛部的結(jié)果,紅色圓圈和藍色方塊是實驗測到的數(shù)據(jù)Fig.5.Measured propagators of photons in free space.The red and blue lines are the results of theoretical calculations of the real and imaginary parts of the propagators,and the red circles and blue squares are experimentally measured data.

5 最小作用量原理的實驗演示

傳播子是路徑積分理論中的關(guān)鍵物理量,實現(xiàn)了對傳播子的測量為對路徑積分的基本概念進行實驗研究提供了可能性.其中最小作用量原理是路徑積分中的核心原理,因此基于傳播子的測量演示最小作用量原理是對路徑積分基本概念的最直觀、最接近本質(zhì)的實驗研究.本節(jié)將介紹如何通過傳播子的實驗結(jié)果實現(xiàn)對最小作用量原理的實驗演示.

根據(jù)路徑積分公式(8),傳播子可以通過對所有可能路徑的貢獻進行積分求得,而所有路徑疊加的結(jié)果等同于振幅相位最穩(wěn)定的路徑,該路徑是滿足最小作用量原理的經(jīng)典路徑.通過對實驗所得的路徑振幅進行分析,找出滿足δS/δx(t)0 的路徑,然后將其與通過拉格朗日方程計算出來的經(jīng)典路徑進行對比,若兩者結(jié)果相符合,則驗證了路徑積分中的最小作用量原理.然而,由于δS/δx(t)0是變分方程,對于離散且有限的實驗數(shù)據(jù)而言,尋找滿足這個方程的實驗結(jié)果比較困難,因此有必要把它轉(zhuǎn)化為更加直觀的微分方程.參考文獻[1],路徑可以離散化為相繼發(fā)生的事件,在起點(xa,ta)和終點(xb,tb) 設置一個途徑點(x,t),在此情況下,路徑的振幅可以表示為傳播子的連乘:

這樣路徑振幅便轉(zhuǎn)化為關(guān)于x和t函數(shù).φ對變量x求偏導可得:

因此,在實驗中,只需要測量出傳播子K(xb,tb;x,t)和K(x,t;xa,ta),然后再通過(21)式和(23)式就能確定經(jīng)典路徑在t時刻經(jīng)過的x方向位置.不斷改變t進行測量,就能最終描繪出經(jīng)典路徑xcl(t).事實上,在實驗中這個判據(jù)條件還可以進一步優(yōu)化[4],僅需用K′′(xb,tb;x,t) 和K′′(x,t;xa,ta)的實驗數(shù)據(jù)便能求出經(jīng)典路徑,這樣可以省略波函數(shù)測量的步驟.在這個優(yōu)化后的方案中,假設M,最小作用量原理的判別條件便可表示為

在圖2 所示的實驗中,通過選擇在SLM 上相位調(diào)制位置來確定初始位置xa,將初始位置xa固定,移動CCD 相機的縱向位置來調(diào)節(jié)t,就可測得K′′(x,t;xa,ta).調(diào)整SLM后4f透鏡系統(tǒng)的成像位置,使得t時刻變成的初始時刻,然后通過改變SLM 的相位調(diào)節(jié)位置x,此時x就是變化的起點,終點xb固定,在CCD 上讀取終點xb的測量結(jié)果,便可以測量出K′′(xb,tb;x,t).測到K′′(x,t;xa,ta)和K′′(xb,tb;x,t)之后,利 用(24)式求M(x,t) 在x方向上的極值,就可以得到經(jīng)典路徑xcl(t).

光子在自由空間中的經(jīng)典路徑如圖6 所示.選取初始位置xa0 作為固定起點,選取xb{-0.08 mm,0,0.08 mm}這3 個終點位置.圖6 中的實線是根據(jù)拉格朗日方程計算出自由空間中光子傳播的經(jīng)典路徑,可見在經(jīng)典力學中,自由傳播粒子的經(jīng)典路徑是直線.其中離散的點是通過實驗測量的傳播子通過(23)式計算得到不同中間時刻的經(jīng)典路徑所在位置,實驗中選取了7 個中間時刻進行測量,x方向的測量間隔為 2.66 μm,誤差棒表示3 次重復實驗的標準差.從圖6 可以看出,實驗結(jié)果與理論結(jié)果高度一致,這意味著通過傳播子的實驗數(shù)據(jù)準確地得到了光子自由空間中的經(jīng)典路徑.

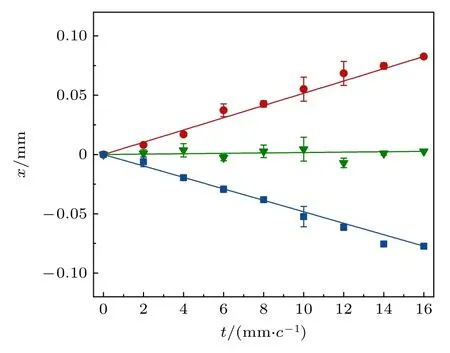
圖6 由最小作用量原理得到的光子自由演化時的經(jīng)典路徑.實線展示的是理論計算所得的自由演化的經(jīng)典路徑,離散點為通過傳播子的實驗數(shù)據(jù)求得的自由演化的經(jīng)典路徑位置Fig.6.The classical path of photons in free evolution derived from the principle of least action.The solid line shows the classical path in free evolution obtained from the theoretical calculation,and the discrete point is the classical path position in free evolution obtained from the experimental data of the propagator.

對于光子的傳播而言,勢能函數(shù)與折射率相關(guān),選取橫向折射率為二次型函數(shù)分部的光學材料(GRIN 透鏡)放置于圖2(b3)所示的相應位置中,那么光子傳播的哈密頓量就變?yōu)?其中ω ≈0.208(c/mm).在此情況下,可測量光子在諧振勢中演化的傳播子,然后再利用(24)式得到光子在諧振勢場中的經(jīng)典路徑,實驗結(jié)果如圖7 所示.選取3 個起點位置xa{-0.053 mm,0,0.053 mm}和一個固定終點位置xb0,通過拉格朗日方程可以求出相應的3 條經(jīng)典路徑,如圖7 中的實線所示,而圖中的離散點則為實驗結(jié)果,實驗中路徑演化的總時長為 1.5 π/ω,其中每隔 0.1 π/ω選取一個中間時刻點測量得出對應的經(jīng)典位置,誤差棒表示3 次重復實驗的標準差.從結(jié)果可看出,通過實驗所測的傳播子數(shù)據(jù)準確地得到了光子在諧振勢中的經(jīng)典路徑.

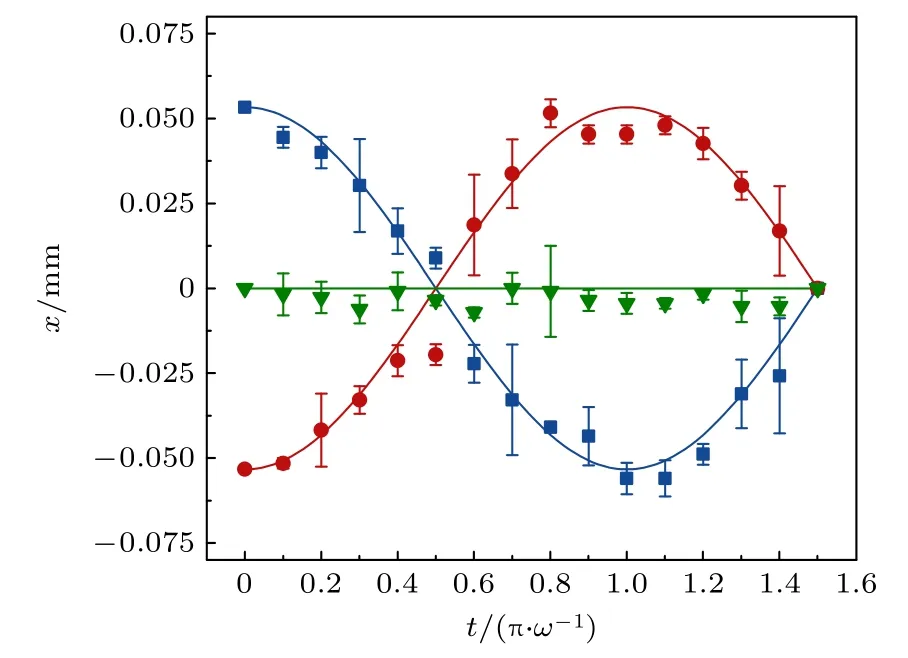
圖7 在諧振子勢場中的經(jīng)典路徑.實線展示的是理論計算所得的在諧振勢中的經(jīng)典路徑,離散點為通過傳播子的實驗數(shù)據(jù)求得的在諧振勢中的經(jīng)典路徑位置Fig.7.Classical trajectories in the harmonic potential.The solid line shows the classical path in the harmonic potential obtained by theoretical calculation,and the discrete point is the classical path position in the harmonic potential obtained by the experimental data of the propagator.

圖6 和圖7 的結(jié)果表明,通過傳播子測量技術(shù),可以在路徑積分的框架下演示最小作用量原理.最小作用量原理是物理學中的普適性原理,路徑積分把這一原理引入到量子力學中,對量子理論做了一個全新的闡述.實驗演示最小作用量原理是傳播子測量的一個重要的應用范例,它有望為此后基于路徑積分表述探索量子-經(jīng)典、量子-廣義相對論等交叉領域的研究提供新的思路.

6 總結(jié)與展望

本文綜述了傳播子測量的理論和實驗進展,介紹了傳播子測量在量子力學中最小作用量原理演示中的應用.傳播子是費曼路徑積分的關(guān)鍵物理量,實現(xiàn)傳播子的實驗測量有重要的科學意義,它為路徑積分相關(guān)的量子現(xiàn)象的實驗研究鋪平了道路.在當今物理學界,路徑積分是多個研究領域中的重要理論基礎,它在描述量子場論、量子多體、量子引力、凝聚態(tài)物理等多個方向的物理現(xiàn)象中有著獨特的優(yōu)勢,因此傳播子的測量技術(shù)有望在日后應用到這些基礎物理問題的觀測和量子模擬的研究中.此外,本文介紹的基于傳播子測量得出光子經(jīng)典路徑的方法,也有望為一些經(jīng)典-量子交叉領域的研究提供新的思路.在光學實驗中,已經(jīng)首次成功測量了傳播子.當前,物理學界對多種不同類型的量子系統(tǒng)的操控和測量技術(shù)正在快速發(fā)展.因此,將傳播子的測量技術(shù)推廣至其他熱門量子實驗系統(tǒng)中,也是一個有意義的研究方向.路徑積分傳播子具有廣泛的應用,本綜述對將來進行傳播子測量技術(shù)的研究有參考價值.