石墨烯類超導體的單磁性雜質效應*

趙宗陽 李銘 周濤

(華南師范大學物理學院,廣東省量子調控工程與材料重點實驗室,粵港量子物質聯合實驗室,廣州 510006)

超導體的磁性雜質效應以及其中存在的束縛態(即Yu-Shiba-Rusinov 態)一直受到較多的關注.最近,在實驗室中,成功發現了石墨烯類超導材料中Yu-Shiba-Rusinov 態的存在.本文在實空間建立描述石墨烯材料超導態的有效哈密頓量,考慮單個磁性雜質,構造Bogoliubov-de Gennes(BdG)方程,并對超導序參量做自洽計算,在此基礎上,理論研究了石墨烯類超導體的磁性雜質效應.計算結果顯示,僅當超導的配對對稱性是傳統的s 波配對時,能隙內會出現Yu-Shiba-Rusinov 束縛態,束縛態的位置以及強度和雜質的磁矩有關,且強度顯示出了明顯的正負非對稱性,但對于p+ip 和d+id 配對對稱性,則不存在能隙內的束縛態.本文的理論計算結果一方面對實驗現象做了合理解釋,另一方面指出了石墨烯和傳統超導組成的異質結系統,石墨烯層由于臨近效應誘導出來的超導配對項仍然是s 波配對.

1 引言

由于二維的石墨烯材料具有獨特的物理特性以及廣闊的應用前景,近20 年來其物理性質受到了廣泛的關注[1].一個重要的研究方向是在石墨烯類材料中實現超導電性.理想的石墨烯材料是一種半金屬材料.沒有超導電性,但近年來在實驗室中已通過多種輔助途徑在石墨烯類材料中成功實現超導電性,有效的手段包括:通過插入其他原子層的方法實現超導電性[2,3],在雙層和三層石墨烯材料中通過外加電場和磁場的方法誘導出超導電性[4,5],在雙層和三層魔角石墨烯中實現超導電性[6,7],以及用超導材料和石墨烯材料構成異質結,通過鄰近效應在石墨烯材料中實現有效的超導配對項[8,9].

對于超導體材料,一個核心的研究內容是探索其配對對稱性.對于石墨烯類超導體,過去十幾年來,很多研究組理論探索了它可能的配對對稱性.目前主要候選配對對稱性是p+ip 配對[10,11]和d+id 配對[12-15].另一方面,對于超導體和普通金屬組成的異質結系統,由于鄰近效應,通常會在普通金屬材料中誘導出有效的超導配對項.一般認為,誘導出的超導配對項對稱性應與原超導體的配對對稱性相同.但是,在石墨烯材料中,實驗測量得到結果卻并非必然如此.實驗中,將石墨烯材料放在電子型摻雜銅氧化合物超導體Pr2-xCexCuOx上形成異質結,通過掃描隧道光譜實驗得到其局域電子態密度的信息,結果顯示石墨烯中誘導出了p 波對稱性[9],而原銅氧化合物超導體卻是d 波對稱性,兩者的配對對稱性并不相同,因此,即使對于石墨烯-超導的異質結系統,其配對對稱性也是一個值得研究的課題.

雜質效應往往可以用來作為判斷超導體配對對稱性的有力工具,比如在某些對稱性下,雜質可以導致能隙內的束縛態[16].在過去幾年,理論研究者對石墨烯材料中的雜質效應有過一定的關注[17-19],其中的束縛態的存在被建議可以用來判斷石墨烯材料的配對對稱性.而本文主要關注石墨烯超導體的磁性雜質效應.事實上,超導體中的磁性雜質效應一直是一個重要的研究方向,早在1960 年代,于祿[20],Shiba[21]和Rusinov[22]分別獨立地通過理論計算提出超導體中磁性雜質周圍會存在能隙內的束縛態,Yu-Shiba-Rusinov態(簡稱為YSR 態).需要指出的是,YSR 態與雜質原子的局域磁矩密切相關,所以YSR 態背后的物理原因與上述非磁性雜質誘導出的束縛態完全不同[16-18].1997年,YSR 態的存在被實驗證實[23].在石墨烯類超導體中,理論預測可以通過氫化的方法引入局域磁矩,進一步的計算預測了YSR 態的存在[24].最近,實驗上對石墨烯類超導體的YSR 的觀測也有了進展,在一個石墨烯和傳統的鉛超導體的耦合系統中,在晶界附近觀測到了YSR 態的存在[25].

理論計算顯示,在石墨烯材料的晶界附近會引入磁性的點缺陷[26-28],因此,理論上可以通過單個磁性雜質附近的局域電子結構來定性模擬晶界附近的電子結構并進一步研究YSR 態.對超導體的單個雜質效應的研究通常有兩種有效的方法,一種是忽略雜質對超導序參量的影響,近似認為超導序參量均勻分布,將哈密頓量分為均勻項和雜質項兩個部分,其中均勻部分可以進行傅里葉變換到動量空間,雜質項可以視作微擾或者一個散射中心處理,在T 矩陣或者微擾論結合戴遜方程的基礎上獲得系統的格林函數,進一步可以研究系統的其他性質[16,17,24].這種方法的缺點是忽略了序參量的空間漲落,尤其是我們通常關心雜質附近的局域特性,而雜質附近的超導序參量往往被壓制了.優點是格林函數有很好的解析形式,可以根據格林函數分母的零點分析能隙內束縛態產生的原因,且在動量空間處理問題,不存在尺寸效應.

早期,針對石墨烯超導態,有研究組運用T 矩陣的方法研究了單個磁性雜質效應[19],計算結果表明:僅僅在雜質原子的磁交換作用大于石墨烯的能帶寬度時,YSR 態才出現.這一條件在實際材料中比較難滿足.但是由于T 矩陣方法忽略了雜質對超導序參量的壓制,所以該方法雖然可以定性地研究雜質效應,但是,雜質的作用有可能會被低估.理論上存在著另一種研究雜質效應的方法,就是實空間的 BdG 方程方法[18,29,30],采用這種方法需要在實空間寫出整個哈密頓量,自洽求解實空間所有格點的超導序參量,進一步用實空間對角化的方法求解系統的實空間格林函數.這種方法的缺點是只能在有限大小的系統中計算,具有一定的尺寸效應,且沒有辦法進一步理論分析束縛態產生的原因,優點是進行了全空間對角化,且充分考慮了雜質對序參量的影響,結果較為精確.在過去石墨烯超導體的非磁性雜質的理論研究中,這兩種方法都被采用[17,18],結果定性上大體相同,但細節處仍然有較多的差異.

本文采用了實空間BdG 方程的方法結合自洽計算來對石墨烯材料的磁性雜質效應進行理論研究.由于實驗上YSR 是在石墨烯和傳統超導體耦合系統中發現了YSR態,可判斷該實驗中石墨烯材料誘導出的配對對稱性有比較大的概率也是傳統的s 波配對.所以本文主要研究也是基于傳統的s 波配對.計算結果顯示,s 波配對的石墨烯超導體具有明顯的YSR 束縛態,其性質定性符合實驗結果.另一方面,也研究了p+ip 和d+id 配對的石墨烯超導體的磁性雜質效應,計算結果和s 波配對有非常大的區別,對于這兩種配對對稱性,并沒有出現明顯的YSR 態.結果一方面表明,磁性雜質效應可以作為判斷石墨烯類超導體配對對稱性的一個有力的工具,另一方面,和最近發表的實驗結果相比較,本文結果說明,石墨烯和傳統超導體組成的異質結其鄰近效應誘導出來的石墨烯中的超導配對仍然是傳統的s 波配對.這一結果有別于石墨烯-電子型銅氧超導體異質結的情況.

2 理論模型

我們的出發模型包含正常態項、超導配對項和磁性雜質項,總的哈密頓量可表示為

其中,tij表示i格點和j格點之間的跳躍,實際計算中,取最近鄰格點之間的跳躍,σ表示電子的自旋,μ是化學勢.

如果是d+id 或者p+ip 配對,超導配對項可表示為近鄰格點之間的配對：

〈ij〉表示j格點在i格點的最近鄰.

Js為雜質點自旋和石墨烯格點上傳導電子的交換耦合常數[29,30].

考慮實空間共有N個格點,超導態總的哈密頓量可以寫成 2N×2N的矩陣形式,可以列出如下的BdG 方程:

其中,Hij-tij-μδij,來自正常態哈密頓量的貢獻,如果是d+id 和p+ip 配對,配對項需滿足額外的約束條件,即ΔjiξΔij,其中,ξ+1 或者ξ-1,分別對應d+id 配對和p+ip 配對.ujm和vjm是哈密頓量矩陣的本征矢中的分量,Em是哈密頓矩陣的本征值,均可通過對角化哈密頓量矩陣求得.

根據BdG 方程,可以自洽地求解超導序參量,如果考慮超導項是起源于同一個格點上的電子間的有效吸引相互作用,吸引勢為V,這種情況是s 波配對,自洽方程可以表示為

對于p+ip 配對和d+id 配對,超導項是來自最近鄰格點之間的有效吸引相互作用,同樣考慮吸引勢為V,自洽方程可以表示為

在自洽地求解得出每一個格點的超導序參量之后,可以進一步計算格點上的粒子數ni,以及局域磁矩mi,由于自旋磁矩和自旋角動量成正比,可采用自旋角動量z方向平均值Sz表示局域磁矩:

最后,可以得出格點i處的局域電子態密度ρi(ω)的表達式:

在下文計算結果展示中,取最近鄰格點的躍遷常數為能量的單位,即tijt1(i和j為最近鄰格點).在自洽計算中,配對勢V的大小決定了超導能隙的大小,兩者是單調遞增的關系.通常來說,超導能隙大小不改變雜質效應的定性行為,但是超導能隙越小,Γ就需要越小,這樣才能使得能隙內的特征被更好的展示.但是Γ太小,會使得LDOS 曲線急劇振蕩,所以,通常理論計算會取一個相對大的配對勢,這樣Γ也可以取得較大,使得曲線平滑且能隙內的特征更加明顯[17],本文取V2.15和Γ0.01.化學勢取值決定了電子濃度的大小,由于實驗中運用鄰近效應在石墨烯中實現超導電性[25],可以預計摻雜濃度較小,這里也考慮低摻雜的情況,選取化學勢μ0.4.在計算局域電子態密度的時候,采用 10×10 的超原胞.我們已經通過數值計算進行仔細驗證,當參數在實驗允許的范圍發生合理的變化時,結果定性的行為不發生變化.

3 計算結果和討論

本文重點討論石墨烯材料在s 波超導態下的磁性雜質效應,首先根據(7)式的超導序參量的自洽方程,考慮同一個格點上存在有效吸引勢V,在Js0.6時,自洽求解得到超導序參量的空間分布.結果展示在圖1,其中,序參量的大小用格點的顏色表示,藍色點是雜質所在位置.

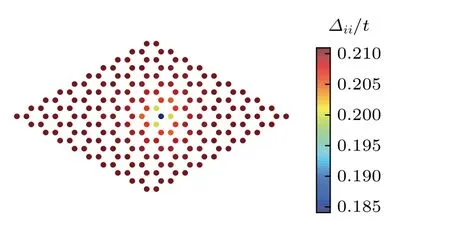
圖1 根據(7)式自洽計算得到的s 波超導序參量的空間分布Fig.1.Spatial distribution of the superconducing order parameter based on the self-consistent calculation [Eq.(7)].

如圖1 所示,在雜質點附近,超導序參量在一定程度上被壓制.序參量在雜質點處達到最小值,在這里,雜質對超導序的壓制,主要是由于局域磁矩的影響.通常,超導序和磁性總是互相競爭的關系,局域磁矩的存在一定會壓制超導電性.但另一方面,根據自洽結果可以看出,雜質對超導序的影響范圍并不大,當格點遠離雜質點時,序參量慢慢增加,當格點距雜質點超過兩個晶格常數的距離之后,序參量大小恢復為均勻值.因此,可以合理地預期,不需要太大的格點系統就可以得到比較準確的結果.本文通過數值驗證了這一點,在考慮的原胞數從 6×6 慢慢增加到 20×20 之后,得到的結果并沒有明顯差別.

我們進一步研究雜質對粒子數以及局域磁矩的影響,根據(8)式和(9)式,計算了平均粒子數和局域磁矩在實空間的分布,計算結果在圖2 展示.對于粒子數和雜質的關系,如圖2(a)所示,雜質的存在對粒子數影響很小,整個空間粒子數分布接近均勻(均在1.04—1.05 之間).這是因為在計算中僅僅考慮了雜質帶來的磁效應,忽略了雜質的非磁散射項.另一方面,從圖2(b)可以看出,在雜質點上,有明顯的局域磁矩存在,在雜質最近鄰點,局域磁矩急劇減小.在距離更遠的地方,局域磁矩消失.眾所周知,超導體中局域磁矩的存在可能會導致YSR 態的出現[20-22].但是目前根據局域磁矩在空間的分布,我們可以預期,如果單個磁性雜質確實可以誘導出YSR態,則僅僅在雜質點以及雜質的最近鄰點可以看到明顯的YSR 共振峰.

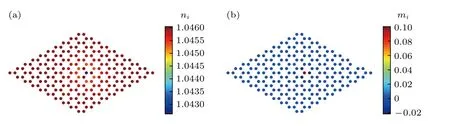
圖2 (a) 平均粒子數 ni 的空間分布;(b) 局域磁矩 mi 的空間分布Fig.2.(a) Spatial distribution of the on-site particle number ni ;(b) spatial distribution of the local magnetic moment mi.

我們展示磁性雜質附近局域電子態密度的計算結果.首先看s 波配對的情況,圖3(a),(b)分別展示了雜質點以及雜質最近鄰格點處局域電子態密度和能量之間的關系.在雜質點處,如圖3(a)所示,隨著雜質項的引入,當Js0.6時,在能隙內,出現了額外的共振峰,隨著Js變大,共振峰往費米能處移動,在Js2時,共振峰出現在非常接近費米能的低能位置.此外,研究結果顯示,共振峰總是成對出現的,并且出現的能量始終是正負對稱的,這是起源于超導體的電子空穴對稱性.另一方面,共振峰的強度是正負不對稱的.

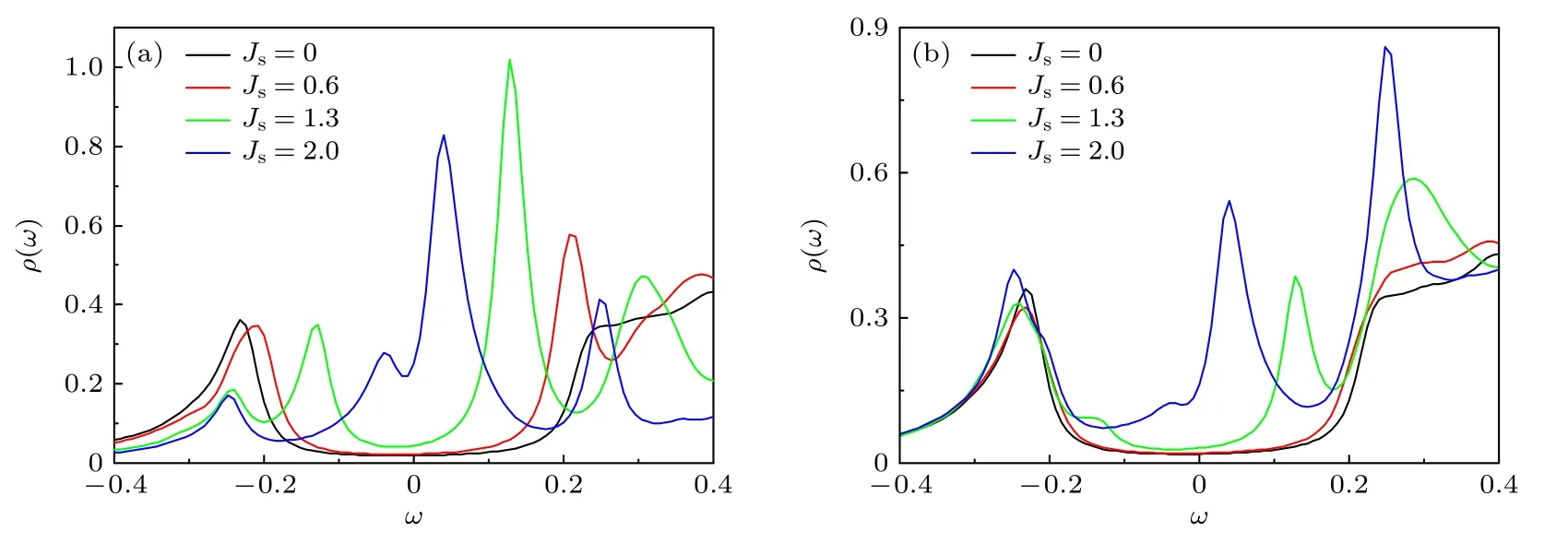
圖3 s 波配對情況下磁性雜質附近的局域電子態密度的計算結果(a) 雜質點位置的局域電子態密度;(b) 雜質最近鄰格點上的局域電子態密度Fig.3.Numerical results of the local density of states near the magnetic impurity site for the s-wave graphene based superconductor:(a) The local density of states at the impurity site;(b) the local density of states at the nearest neighbor site of the impurity.

在雜質的近鄰格點,如圖3(b)所示,和雜質點的局域電子態密度類似,當Js0時,出現了明顯的能隙內的共振峰.和雜質點上的計算結果相比,共振峰的位置沒有發生變化,但是,共振峰的強度明顯減小.通過數值驗證了在距離雜質更遠的格點,共振峰幾乎消失,這一結果也與圖2(b)所展示的局域磁矩的計算結果一致.以上共振峰的性質符合YSR 態的特性[20-22].最近,實驗上在石墨烯超導材料的晶界附近觀測到了YSR 態的特征[25],實驗結果顯示:共振峰的強度具有正負不對稱的特性,且共振峰的位置依賴于磁交換作用J的大小,圖3 中展示的理論計算結果和實驗結果定性一致.

之前,在T-矩陣的基礎上,針對石墨烯超導材料的磁性和非磁性雜質效應有過系統的理論研究.有必要將計算結果與T 矩陣的結果進行定性的比較.對于磁性雜質,基于T 矩陣的理論計算顯示,在磁性雜質勢不是足夠強時,不存在能隙內雜質態,能隙內的雜質態僅僅在雜質勢超過能帶寬度W(石墨烯的能帶寬度約為6),雜質態才會出現,并且雜質態的位置和雜質勢大小密切相關.在本文計算中,在雜質勢J=0.6 的時候,雜質態已經出現,顯然,基于BdG 方程方法得到的雜質效應要顯著得多.由于BdG 方程是全空間的自洽計算,充分考慮了雜質對序參量的影響,所以分析認為,BdG 方程的計算結果更加接近于實際情況.

進一步研究d+id 和p+ip 配對對稱性情況下的磁性雜質效應,考慮最近鄰格點之間存在有效吸引勢V,根據(8)式自洽計算超導配對序參量,在自洽計算基礎上進一步根據(11)式計算局域電子態密度.圖4(a)和圖4(b)分別展示了d+id配對時,雜質點上和雜質近鄰格點的局域電子態密度的計算結果,圖4(c)和圖4(d)是相應的p+ip 配對對稱性時的計算結果.如圖所示,對于這兩種配對對稱性,始終沒有YSR 態的出現.本文結果表明,對于單層石墨烯超導體,僅僅在s 波超導態中存在YSR態,這一方面解釋了最近的實驗結果[25],另一方面,也明確了該實驗中石墨烯材料中由于臨近效應導致的有效配對是s 波對稱.

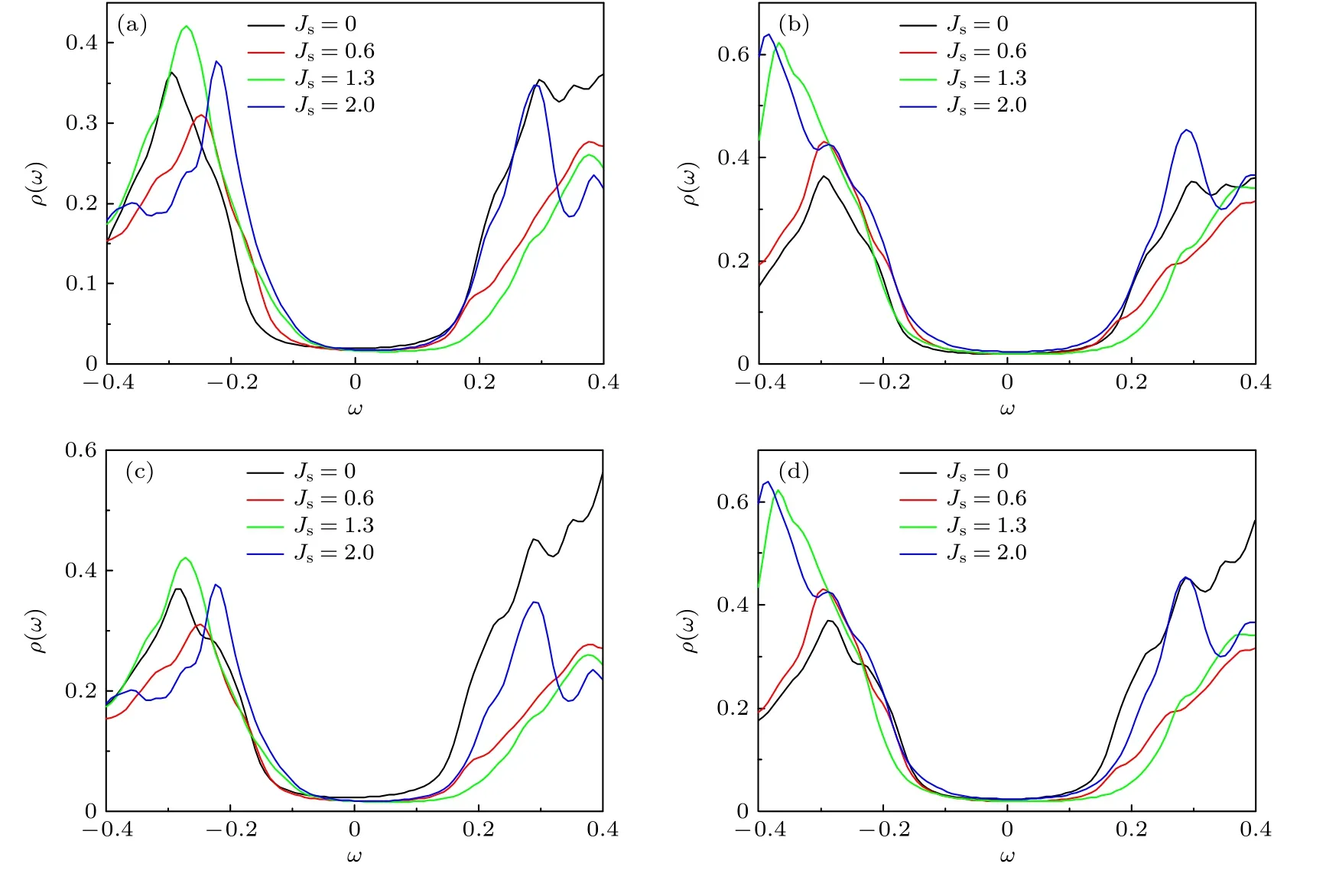
圖4 d+id 波和p+ip 波配對情況下磁性雜質附近的局域電子態密度的計算結果(a) d+id 配對雜質點位置的局域電子態密度;(b) d+id 配對雜質最近鄰格點上的局域電子態密度;(c) p+ip 配對雜質點位置的局域電子態密度;(d) p+ip 配對雜質最近鄰格點上的局域電子態密度Fig.4.Numerical results of the local density of states near the magnetic impurity site for the d+id-wave and p+ip-wave graphene based superconductor:(a) The local density of states at the impurity site for the d+id pairing symmetry;(b) the local density of states at the nearest neighbor site of the impurity for the d+id pairing symmetry;(c) the local density of states at the impurity site for the p+ip pairing symmetry;(d) the local density of states at the nearest neighbor site of the impurity for the p+ip pairing symmetry.

我們有必要討論石墨烯超導中磁性雜質效應和非磁性雜質效應的不同.本文主要討論的是低摻雜濃度的石墨烯超導體,在這一摻雜區域下,對于非磁性雜質,根據之前T 矩陣的理論計算結果[17],當配對對稱性為s 波和p+ip 波時,均不存在能隙內的雜質態,當配對對稱性為d+id 配對時,非磁性雜質會誘導出能隙內的共振態,但是其性質和磁性雜質誘導的YSR 態具有明顯區別.非磁性雜質誘導出來的共振態,共振峰的位置相對比較穩定,隨著雜質勢的變化僅僅有輕微的移動.

雜質態產生的位置和原因,通常可以根據T矩陣的方法來分析,對于超導體,由于能隙的存在,通常T 矩陣分母的虛部在能隙內會很小,如果在低能量時T 矩陣分母實部也穿過零點,就會出現能隙內的共振態.在過去基于T 矩陣方法對雜質效應的研究中,已經廣泛地通過研究T 矩陣分母來討論雜質態產生的機制[16,17].但是,由于本文是基于BdG 方程的方法研究雜質效應,目前無法進一步給出雜質態產生,以及s 波和其他兩種配對對稱性磁性雜質效應計算結果不同的物理原因,背后的物理機制需要進一步研究.

4 結論

本文在實空間BdG 方程的基礎上,研究了石墨烯超導體的磁性雜質效應.考慮磁性雜質破壞了系統的平移對稱性,在平均場的基礎上自洽計算了超導序參量.在此基礎研究了磁性雜質附近的局域電子態密度計算結果表明,在超導配對是傳統的s 波配對時,磁性雜質附近出現了YSR 態.但對于p+ip 配對和d+id 配對,則沒有出現任何能隙內的共振態.

針對s 波超導體的理論計算結果和近年來在石墨烯-傳統超導體組成的異質結系統中發現的YSR 態的實驗結果定性一致.一方面解釋了實驗現象,另一方面促進了我們對石墨烯類超導體的理解.同時本工作仍然存在一些不足,其中最主要的不足是在BdG 方程的框架下,無法對YSR 態的成因以及產生條件做進一步的理論分析.這是BdG方法研究雜質效應的缺點.我們預期,如果從T 矩陣的角度研究磁性雜質效應,能夠解決這一不足,給出能隙內束縛態的成因,并討論其產生條件,這也是我們下一步研究工作的方向.