科研實踐與課程教學相互融合的信號與系統課程實驗改革

鐘曉蕓

(廣西師范大學電子與信息工程學院，廣西 桂林 541004)

0 引言

信號與系統課程是電子信息類專業必修的重要專業課程之一，高等數學、電路和復變函數等是它的先修課程,而其后續課程則有數字信號處理和自動控制原理等[1-2]。該課程既是信號處理領域的入門課程,也包含后續課程學習及學生考取研究生的重要基礎理論，其特點是概念抽象較難理解,數學推導復雜較難掌握,結果靈活較難運用。該課程的理論性和實踐性都較強,其課程目標主要是使學生獲得連續系統的時域分析和s域分析、離散系統的時域分析、傅里葉變換和系統的頻域分析、拉普拉斯變換、系統狀態動力學分析等,同時提高學生的實踐能力。考慮到該課程涉及較多的現代數學知識,概念抽象,內容靈活,沒有一定的養成訓練和實驗試探,相當多的同學會對其原理和方法感到難以正確把握，特別是對于課程中諸如時域分析和頻域分析以及系統動力學特征等重要的知識點和較難掌握的內容，僅通過教師傳統課堂的教學,容易造成學生們不愿意手工求解，或者對原理的運用不得要領。

為此,文章在課程實驗的教學環節中有針對性地結合若干經過簡化的科研前沿問題，引入若干Matlab仿真實驗,引導學生通過計算機編程完成數值仿真，以便可視化地演示課程的一些基本原理及方法,達到科研實踐與課程教學相互融合,增強學生在計算機軟件的配合下正確把握課本知識,適當開展一定的科學探索的目的。實踐表明，由于結合一些適當簡化的科研前沿問題，加上Matlab程序設計語言非常簡潔而高效，可以很快掌握，極大調動了學生自己進行課程實驗的積極性。大家主動參與實驗、自己試著編寫M程序實現對所學基本原理和方法進行實驗驗證，包括對于文獻上的一些可類比的新結果進行檢驗，有效地促進了學生創新能力的提升。客觀上，由于Matlab軟件不僅運算能力強大,而且計算精度特別高,其數值計算誤差可以調節。這些特點使得Matlab 仿真結果能夠真實地反映與理論分析的一致性,相比傳統的課程實驗教學具有明顯的創新優勢。通過這些實驗,將有助于學生理解和運用現代信號與系統課程的基本原理和方法,獲得利用Matlab仿真解決現代分數階系統的初步科研訓練。

1 基于科研實踐與課程教學相互融合的課程實驗設計

基于科研實踐與課程教學相互融合理念[3]，結合Matlab仿真開展信號與系統課程實驗的設計，有效打破了以在實驗中大量使用硬件和常規問題為特征的傳統實驗教學的局限性,實驗項目設計可以很容易地觸及科研前沿內容，同時聯系到連續或離散系統的時域仿真和頻域分析等理論課程中的難點和重點,學生們通過編寫M程序并自己上機進行測試分析,不僅增加了實驗設計的前沿性和實驗項目選擇的靈活性,而且使得信號與系統的計算可以直觀演示。這樣,在開展信號與系統課堂理論學習的同時,通過計算機的配合,不僅學會Matlab 基本的編程技巧和實現方法,而且嘗試將體現課程基本原理的重難點習題及通過將課本中的一些連續信號系統的狀態方程進行分數階推廣。具體來說,我們結合若干課程實驗內容的分數階推廣并且借用Matlab 程序和仿真演示，給學生布置一些應用Matlab語言的課程習題作為實驗作業,不僅有利于提高學生的學習興趣,培養學生綜合運用計算機輔助分析實際控制系統的科研創新能力,而且有利于加深對信號與系統課程的基本原理、基本方法的理解。

1.1 應用Matlab 語言進行仿真

在課程實驗中應用Matlab 進行分數階的信號和系統的可視化繪圖,主要使用到plot,stairs,stem,jieyue,即階躍函數等,以及一些簡單的拉普拉斯變換及其逆變換的Matlab 求解命令laplace，ilaplace 的分數階實現。

1.2 分數階連續時間系統的穩定性、時域分析及頻域分析

與經典的整數階系統類似，簡單分數階非線性系統的穩定性分析方法最主要的也是根軌跡法和李雅普諾夫方法。根軌跡法主要通過雅可比迭代法分解法計算系統雅可比矩陣A的特征值λ(A),并且根據其分布情況判定系統的穩定性,如果涉及導數的階為分數階α∈(0,1],且arg(λ(A)) >πα/2 時,可判定系統是穩定的。李雅普諾夫方法主要通過判別滿足PA+ATP=-Q的矩陣P的性質判斷系統是否穩定。這些分析方法涉及Matlab 函數主要有:時域分析函數，比如，impulse.m、step.m 和lsim.m。頻域分析分析函數，比如bode.m、nyquist.m和freqs.m等。其中，impulse 函數和step函數來求解LTI系統的沖激響應和階躍響應數值解,而lsim 函數來對LTI 系統的零狀態響應進行數值仿真。step(sys)函數既可以求解系統的單位階躍響應，也可以繪制響應波形圖，impulse(sys)函數既可以求解系統的單位沖激響應，也可以繪制響應的圖形，其他M 函數還有mtimes.m、plus.m 和feedback.m等,還可以利用Simulink，通過仿真求解。

1.3 分數階控制系統控制器設計

分數階微積分誕生于三百年前，主要研究任意階次的微分和積分的特性及其應用問題。分數階控制系統已成為現代非線性控制理論的一個不可或缺的部分[4-5]。隨著分數階系統在現代實際工程領域的作用日益凸顯,目前，分數階非線性系統的研究已經引起了越來越多的學者的興趣。其主要原因在于分數階系統自身具有的特性，即分數階系統具有記憶特性，這是整數階系統所沒有的，所以研究含有分數階微分或積分環節的控制系統在工程應用中愈發重要。

2 基于科研實踐與課程教學相互融合理念結合Matlab軟件設計模擬電路實驗舉例

本文以一個經簡化后的工程問題中的分數階的均勻RC線連接的電壓源模擬電路[5]的波動為例,說明基于Matlab的教學實驗的具體設計內容。圖1顯示的電路系統表示了電壓源的內部傳統電感L= 1H與一個非常長的(l≈∞)均勻RC傳輸線的連接。該電路的波動特征可由以下簡單的微分方程表示-σ0u(t) +σ0e(t),其中，σ0=L-1C-1R, 0 <α≤2。如果α= 1.5,相應的系統的動力學特征在文獻[5]中進行了詳細研究,如果系統的階α= 1.0,相應的整數階系統就是熟悉的經典RC電路模型。在σ0= 0.1,e(t) = 10e-t的情形,由此實現傳統的教材內容與前沿的分數階系統研究適當結合起來。

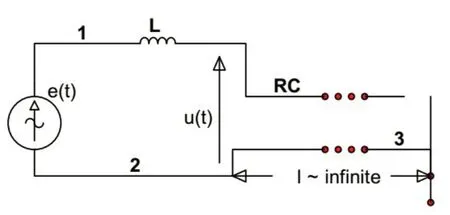
圖1 仿真系統電路圖

通過如下的Matlab 語言：

可以得到均勻RC線連接的電壓源模擬電路的仿真結果如圖2(a) 所示。改變系統的設置，當σ0= 0.1,e(t) =cos(0.4t)時，該電壓源模擬電路的時間波形如圖2(b)所示。

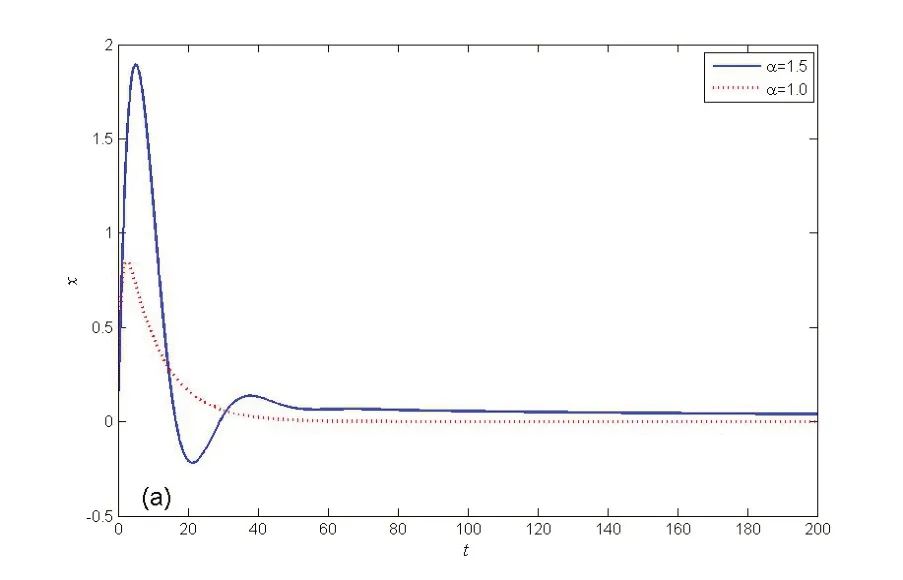
圖2 電路系統的動力學特征仿真波形圖

3 實驗反思

本課程實驗中電路系統的動力學特征仿真在計算機上模擬進行，同時將表征系統特征的微分方程的階處理為一個在0到1之間取值的分數參數進行實驗結果分析。參加實驗的學生在教師的指導下，針對不同的分數階取值選擇，通過仿真波形圖直觀地發現分數階的改變對于電路特征的影響。實驗過程中，通過采用圖1所示的仿真系統電路盡可能地降低實驗復雜度，忽略了實驗環境噪聲以及隨機性因素的影響，體現在系統的微分方程模型中，方程的右邊關于電路狀態變量的函數是簡單的一次函數。鼓勵學生在完成實驗后，探索其他的方法進一步提高仿真精度，比如考慮對應的隨機系統或者將高斯白噪聲考慮進去，還可以進一步考慮模糊控制。結合實驗教學讓學生注意，在復雜而艱辛的科學研究過程中，對科學問題進行適當的簡化無論是對于成功獲得理論研究成果還是有效獲得實驗現象都是非常必要的。學生可以像科學家那樣，結合自己的學習專業及自己感興趣的方向，選擇自己比較熟悉的課題，在一定的理論分析和結果預測的基礎上，通過編寫計算機程序，比如M 程序，進行計算機仿真研究。嘗試按照科研論文的寫作要求和格式，把課程的實驗報告作為一篇基本符合投稿要求的教學科研論文進行撰寫，不僅給出課程實驗的結果，而且分析產生這些結果的內在機理及其表現形式，探討這些實驗結果與文獻上已經發表的科研結果的聯系與區別。同時，訓練學生的科研語言表達能力，讓他們通過圖書館期刊及CNKI 中國知網了解科技論文的寫作格式和要求，激發他們初步了解和思考自己所學專業的相關科研前沿問題，有效提高科研意識，培養他們從課程內容出發通過引申、變通等方式發現科學問題、通過實驗探索科學問題、通過理論分析解決科學問題的科研創新能力。在這個過程中，教師要及時收集學生對于課程實驗的建議和實驗反饋意見，進一步完善實驗設計，把課程實驗的教學質量提升到一個新的臺階。

4 結束語

科研實踐與課程教學相互融合的實驗教學設計是信號與系統課程實驗教學改革，實現“專創融合”和“思創融合”的重要舉措之一。本文提出基于科研實踐與課程教學相互融合理念結合Matlab 的信號與系統課程實驗教學設計,并給出一個典型實驗說明科研前沿內容與課程基本理論內容如何結合有效進行Matlab 仿真的程序設計與用法。本文所述的分數階電路系統的動力學特征仿真實驗設計是“科研實踐與課程教學相互融合”課程實驗的典型案例之一。它使得同學們在大學本科階段就接觸到與自己專業相同或者相近的學科前沿的若干熱點課題，比如，通過編寫計算機M 程序和對比該實驗電路的整階及分數階動力學特征,獲得機會通過本科課程實驗教學親身體驗一個相對完整的科研過程。這既有助于對《信號與系統》課程內容,特別是系統函數及系統的狀態變量分析的深入理解和掌握,也對學生在計算機軟件的配合下通過實驗探索的體驗促進初步的科研訓練有重要作用。